Deck 1: Basic Concepts
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/306
Play
Full screen (f)
Deck 1: Basic Concepts
1
Determine whether the statement is true or false.
- is the set of odd natural numbers.
- is the set of odd natural numbers.
True
2
Determine whether the statement is true or false.
Every irrational number is an integer.
Every irrational number is an integer.
False
3
List the set in roster form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)
4
Determine whether the statement is true or false.
Some real numbers are integers.
Some real numbers are integers.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the statement is true or false.
Every integer is an irrational number.
Every integer is an irrational number.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the statement is true or false.
The set of integers is an infinite set.
The set of integers is an infinite set.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the statement is true or false.
The set of rational numbers is a finite set.
The set of rational numbers is a finite set.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
8
Determine whether the statement is true or false.
Some rational numbers are integers.
Some rational numbers are integers.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
9
Insert eithernsert either to to make the statement true.
--53 _____ -70
A)
B)
--53 _____ -70
A)
B)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
10
Insert eithernsert either to to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the statement is true or false.
Every whole number is a real number.
Every whole number is a real number.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the statement is true or false.
The intersection of the set of rational numbers with the set of irrational numbers is the empty set.
The intersection of the set of rational numbers with the set of irrational numbers is the empty set.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
13
Determine whether the statement is true or false.
Every rational number is an integer.
Every rational number is an integer.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
14
Insert eithernsert either to to make the statement true.
--6 _____ 3
A)
B)
--6 _____ 3
A)
B)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
15
Insert eithernsert either to to make the statement true.
-6.2 _____ 6.3
A)
B)
-6.2 _____ 6.3
A)
B)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether the statement is true or false.
The union of the set of rational numbers with the set of irrational numbers is the empty set.
The union of the set of rational numbers with the set of irrational numbers is the empty set.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether the statement is true or false.
- is the set of odd natural numbers.
- is the set of odd natural numbers.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the statement is true or false.
Some rational numbers are irrational.
Some rational numbers are irrational.

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
19
Insert eithernsert either to to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
20
List the set in roster form.
-
A){32, 34, 36}
B){31, 32, 33, 34, 35, 36}
C){30, 31, 32, 33, 34, 35, 36}
D){30, 32, 34, 36}
-
A){32, 34, 36}
B){31, 32, 33, 34, 35, 36}
C){30, 31, 32, 33, 34, 35, 36}
D){30, 32, 34, 36}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
21
Illustrate the set on a number line.
-

A)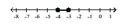
B)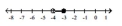
C)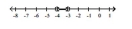
D)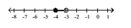
-

A)

B)

C)
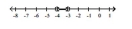
D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
22
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
23
Illustrate the set on a number line.
-
A)
B)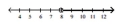
C)
D)
-

A)

B)
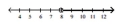
C)

D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
24
Illustrate the set on a number line.
-
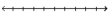
A)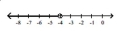
B)
C)
D)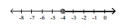
-
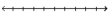
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
25
Illustrate the set on a number line.
-

A)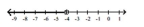
B)
C)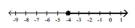
D)
-

A)
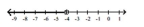
B)

C)

D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem.
The Little Town Dog Club offers a "Puppy Kindergarten" for puppies in their community. In order for a dog to
advance from this introductory class to the first level obedience class, it must consistently demonstrate
knowledge of each of 4 commands. The instructor has the following table in her record book.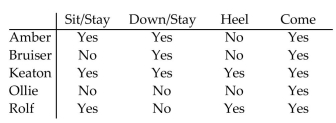 Let A = the set of dogs who have demonstrated knowledge of Sit/Stay.
Let A = the set of dogs who have demonstrated knowledge of Sit/Stay.
Let B = the set of dogs who have demonstrated knowledge of Down/Stay.
Let C = the set of dogs who have demonstrated knowledge of Heel.
Let D = the set of dogs who have demonstrated knowledge of Come.
Give each of the sets A, B, C, and D using roster notation. Determine the set A ∩ B ∩ C ∩ D. Which dogs are ready to
advance to the next level?
The Little Town Dog Club offers a "Puppy Kindergarten" for puppies in their community. In order for a dog to
advance from this introductory class to the first level obedience class, it must consistently demonstrate
knowledge of each of 4 commands. The instructor has the following table in her record book.
 Let A = the set of dogs who have demonstrated knowledge of Sit/Stay.
Let A = the set of dogs who have demonstrated knowledge of Sit/Stay.Let B = the set of dogs who have demonstrated knowledge of Down/Stay.
Let C = the set of dogs who have demonstrated knowledge of Heel.
Let D = the set of dogs who have demonstrated knowledge of Come.
Give each of the sets A, B, C, and D using roster notation. Determine the set A ∩ B ∩ C ∩ D. Which dogs are ready to
advance to the next level?

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
27
Illustrate the set on a number line.
-

A)
B)
C)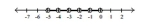
D)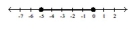
-

A)

B)

C)
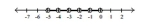
D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
28
List the set in roster form.
-
A){1, 2, 3, 4, 5}
B){0, 1, 2, 3, 4, 5}
C){1, 2, 3, 4}
D){0, 1, 2, 3, 4}
-
A){1, 2, 3, 4, 5}
B){0, 1, 2, 3, 4, 5}
C){1, 2, 3, 4}
D){0, 1, 2, 3, 4}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
29
Express in set builder notation the set of numbers indicated on the number line.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
30
Illustrate the set on a number line.
-

A)
B)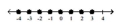
C)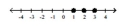
D)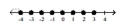
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
31
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
32
-A = { B = {
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
33
List the set in roster form.
-
A){3}
B){3, 4}
C)
D){ }
-
A){3}
B){3, 4}
C)
D){ }

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
34
List the set in roster form.
-
A){1, 4, 8, 12, 16, . . . }
B){0, 4, 8, 12, 16, . . . }
C){4, 8, 12, 16, 20, . . . }
D){8, 12, 16, 20, 24, . . . }
-
A){1, 4, 8, 12, 16, . . . }
B){0, 4, 8, 12, 16, . . . }
C){4, 8, 12, 16, 20, . . . }
D){8, 12, 16, 20, 24, . . . }

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
35
Express in set builder notation the set of numbers indicated on the number line.
-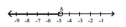 A = -4.8
A = -4.8
A)
B)
C)
D)
-
 A = -4.8
A = -4.8A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
36
Illustrate the set on a number line.
-
A)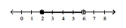
B)
C)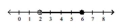
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
37
Express in set builder notation the set of numbers indicated on the number line.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
38
List the set in roster form.
-
A){0, 1, 2, 3, 4, 5, . . . }
B){-4, -3, -2, -1, 0, . . . }
C){1, 2, 3, 4, 5, . . . }
D){-5, -4, -3, -2, -1, 0, . . . }
-
A){0, 1, 2, 3, 4, 5, . . . }
B){-4, -3, -2, -1, 0, . . . }
C){1, 2, 3, 4, 5, . . . }
D){-5, -4, -3, -2, -1, 0, . . . }

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
39
Express in set builder notation the set of numbers indicated on the number line.
-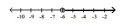
A)
B)
C)
D)
-
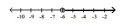
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
-The table shows the students who had a score of 80 or higher on the first two tests in a chemistry class. (Note: Every student in the class had a different first name.) Find the set of students who had a score of 80 or higher on the first or second tests.
A){Linda, Ken, Eloise, Roger }
B){Fred, Ken, Eloise}
C){Linda, Sue, Earl, Roger, Bill, Cal}
D){Fred, Linda, Sue, Earl, Ken, Eloise, Roger, Bill, Cal}
-The table shows the students who had a score of 80 or higher on the first two tests in a chemistry class. (Note: Every student in the class had a different first name.) Find the set of students who had a score of 80 or higher on the first or second tests.
A){Linda, Ken, Eloise, Roger }
B){Fred, Ken, Eloise}
C){Linda, Sue, Earl, Roger, Bill, Cal}
D){Fred, Linda, Sue, Earl, Ken, Eloise, Roger, Bill, Cal}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the absolute value expression.
-
A)-4
B)0
C)8
D)4
-
A)-4
B)0
C)8
D)4

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
-List the elements of S that are integers.
A){-5, 0, 3}
B){3}
C)
D){0, 3}
-List the elements of S that are integers.
A){-5, 0, 3}
B){3}
C)
D){0, 3}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
43
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of I?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of I?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
44
Evaluate the absolute value expression.
-
A)0
B)
C)
D)
-
A)0
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
45
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is I a subset of Q?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is I a subset of Q?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate the absolute value expression.
-
A)
B)
C)0
D)
-
A)
B)
C)0
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
-List the elements of S that are real numbers.
A){-5, 0, 3}
B)
C)
D)
-List the elements of S that are real numbers.
A){-5, 0, 3}
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
48
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of R?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of R?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
-From the Venn diagram, determine the set A.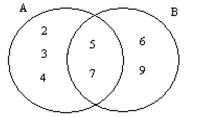
A){5, 7}
B){2, 3, 4, 5, 7}
C){2, 3, 4}
D){2, 3, 4, 5, 6, 7, 9}
-From the Venn diagram, determine the set A.

A){5, 7}
B){2, 3, 4, 5, 7}
C){2, 3, 4}
D){2, 3, 4, 5, 6, 7, 9}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
-List the elements of S that are rational numbers.
A)
B){-5, 0, 3}
C)
D)
-List the elements of S that are rational numbers.
A)
B){-5, 0, 3}
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
-List the elements of S that are whole numbers.
A)
B){-5, 0, 3}
C){0, 3}
D){3}
-List the elements of S that are whole numbers.
A)
B){-5, 0, 3}
C){0, 3}
D){3}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
52
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is H a subset of R?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is H a subset of R?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
53
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of H?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is Q a subset of H?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the absolute value expression.
-|
A)47
B)23.5
C)-23.5
D)0
-|
A)47
B)23.5
C)-23.5
D)0

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
55
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is W a subset of N?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is W a subset of N?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate the absolute value expression.
-
A)0
B)-4
C)4
D)8
-
A)0
B)-4
C)4
D)8

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.
-List the elements of S that are irrational numbers.
A)
B)
C)
D)
-List the elements of S that are irrational numbers.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
58
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is W a subset of Q?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is W a subset of Q?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
59
Let R = the set of real numbers, N = the set of natural numbers, W = the set of whole numbers, I = the set of integers,
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is N a subset of W?
A)Yes
B)No
Q = the set of rational numbers, and H = the set of irrational numbers. Answer the question.
Is N a subset of W?
A)Yes
B)No

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
-List the elements of S that are natural numbers.
A){0, 3}
B){3}
C)
D){-5, 0, 3}
-List the elements of S that are natural numbers.
A){0, 3}
B){3}
C)
D){-5, 0, 3}

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the absolute value expression.
-
A)32
B)0
C)-16
D)16
-
A)32
B)0
C)-16
D)16

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
62
- _________
A)
B)=
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the absolute value expression.
-
A)0
B)-8.7
C)17.4
D)8.7
-
A)0
B)-8.7
C)17.4
D)8.7

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
64
- _________
A)
B)=
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
65
List the values from smallest to largest.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the absolute value expression.
-
A)-1
B)1
C)0
D)undefined
-
A)-1
B)1
C)0
D)undefined

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
67
List the values from smallest to largest.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the absolute value expression.
-
A)0
B)-12
C)24
D)12
-
A)0
B)-12
C)24
D)12

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate the absolute value expression.
-
A)0
B)
C)
D)
-
A)0
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
70
List the values from smallest to largest.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate.
3 + (-14)
A)-17
B)11
C)-11
D)17
3 + (-14)
A)-17
B)11
C)-11
D)17

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
72
List the values from smallest to largest.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
73
- _______
A)
B)=
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
74
- _______
A)
B)=
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
75
List the values from smallest to largest.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
76
- _______
A)
B)
C)=

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
77
-
A)=
B)
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
78
-| _________
A)=
B)
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the absolute value expression.
-
A)
B)
C)
D)0
-
A)
B)
C)
D)0

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck
80
- ________
A)=
B)
C)

Unlock Deck
Unlock for access to all 306 flashcards in this deck.
Unlock Deck
k this deck


