Deck 7: Multivariable Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 7: Multivariable Calculus
1
Tell whether the statement is true or false.
{all odd integers greater than -3 and less than 5} = {-1, 1, 3}
{all odd integers greater than -3 and less than 5} = {-1, 1, 3}
True
2
Provide an appropriate response.
Construct a truth table to determine whether or not the following implication is true: is true: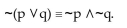
Construct a truth table to determine whether or not the following implication is true: is true:
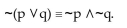

3
Express the proposition as an English sentence and determine whether it is true or false, where p and q are the propositions
p: "9 · 9 = 81" q: "8 · 10 < 7 · 11
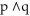
A) 9 · 9 = 81 and 8 · 10 < 7 · 11; false
B) If 9 · 9 = 81, then 8 · 10 < 7 · 11; false
C) 8 · 10 is not less than 7 · 11; true
D) 9 · 9 = 81 or 8 · 10 < 7 · 11; true
p: "9 · 9 = 81" q: "8 · 10 < 7 · 11
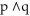
A) 9 · 9 = 81 and 8 · 10 < 7 · 11; false
B) If 9 · 9 = 81, then 8 · 10 < 7 · 11; false
C) 8 · 10 is not less than 7 · 11; true
D) 9 · 9 = 81 or 8 · 10 < 7 · 11; true
9 · 9 = 81 and 8 · 10 < 7 · 11; false
4
Tell whether the statement is true or false.
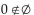
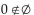

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Construct a truth table for the proposition.
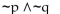
A)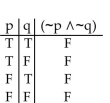
B)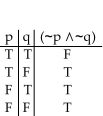
C)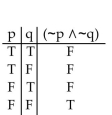
D)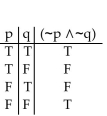
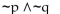
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
Express the proposition as an English sentence and determine whether it is true or false, where p and q are the propositions
p: "9 · 9 = 81" q: "8 · 10 < 7 · 11
The contrapositive of he contrapositive of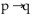
A) If 8 · 10 is not less than 7 · 11, then 9 · 9 is equal to 81; false
B) If 8 · 10 is less than 7 · 11, then 9 · 9 is equal to 81; false
C) If 8 · 10 is not less than 7 · 11, then 9 · 9 is not equal to 81; false
D) If 8 · 10 is less than 7 · 11, then 9 · 9 is not equal to 81; false
p: "9 · 9 = 81" q: "8 · 10 < 7 · 11
The contrapositive of he contrapositive of
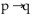
A) If 8 · 10 is not less than 7 · 11, then 9 · 9 is equal to 81; false
B) If 8 · 10 is less than 7 · 11, then 9 · 9 is equal to 81; false
C) If 8 · 10 is not less than 7 · 11, then 9 · 9 is not equal to 81; false
D) If 8 · 10 is less than 7 · 11, then 9 · 9 is not equal to 81; false

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Construct a truth table to decide if the two statements are equivalent.
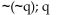
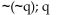

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Construct a truth table to decide if the two statements are equivalent.
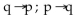
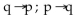

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
Construct a truth table for the proposition and determine whether it is a contingency, a tautology, or a
contradiction: (q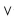 p ) )
p ) ) 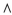 ~q.
~q.
Construct a truth table for the proposition and determine whether it is a contingency, a tautology, or a
contradiction: (q
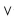 p ) )
p ) ) 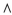 ~q.
~q.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Provide an appropriate response.
Construct a truth table for the proposition and determine whether it is a contingency, a tautology, or a
contradiction: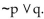
Construct a truth table for the proposition and determine whether it is a contingency, a tautology, or a
contradiction:
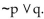

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Provide an appropriate response.
State the converse and contrapositive of the position, "If n is an integer that is a multiple of 15, then n is an
integer that is a multiple of 3 and a multiple of 5."
State the converse and contrapositive of the position, "If n is an integer that is a multiple of 15, then n is an
integer that is a multiple of 3 and a multiple of 5."

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Construct a truth table for the proposition.
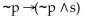
A)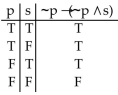
B)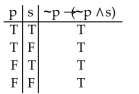
C)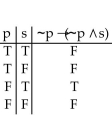
D)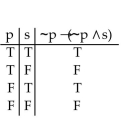
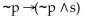
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; D = {2, 5, 8}; and U = {1, 2, 3, 4, 5, 6, 7, 8}. Determine whether the given statement
is true or false.
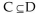
is true or false.
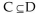

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Construct a truth table for the proposition.
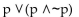
A)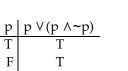
B)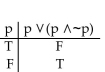
C)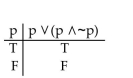
D)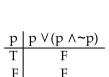
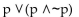
A)
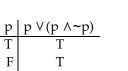
B)
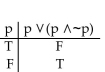
C)
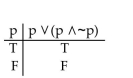
D)
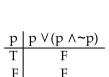

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Tell whether the statement is true or false.
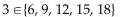
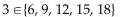

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
Construct a truth table to decide if the two statements are equivalent.
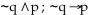
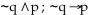

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Construct a truth table for the proposition.
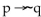
A)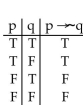
B)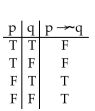
C)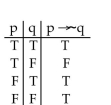
D)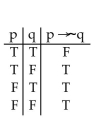
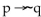
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Tell whether the statement is true or false.
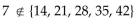
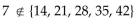

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Construct a truth table to decide if the two statements are equivalent.
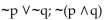
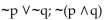

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Construct a truth table to decide if the two statements are equivalent.
~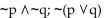
~
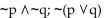

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Determine whether the given set is disjoint or not disjoint. Consider the set N of positive integers to be the universal set, and let 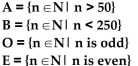
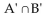
A) not disjoint
B) disjoint
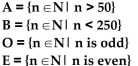
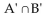
A) not disjoint
B) disjoint

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; D = {2, 5, 8}; and U = {1, 2, 3, 4, 5, 6, 7, 8}. Determine whether the given statement
is true or false.
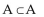
is true or false.
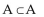

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; D = {2, 5, 8}; and U = {1, 2, 3, 4, 5, 6, 7, 8}. Determine whether the given statement
is true or false.
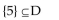
is true or false.
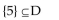

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false.
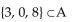
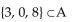

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
n(A) = 33, n(B) = 15, 15,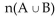 = 42, n(B') = 40. Find
= 42, n(B') = 40. Find 
A) 36
B) 42
C) 49
D) 13
n(A) = 33, n(B) = 15, 15,
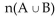 = 42, n(B') = 40. Find
= 42, n(B') = 40. Find 
A) 36
B) 42
C) 49
D) 13

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Use the Venn diagram to find the requested set.
Find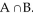 B.
B. 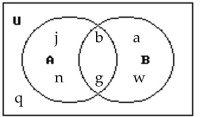
A) {a, b, g, j, q, n, w}
B) {a, b, g, j, n, w}
C) {b, g}
D) {q}
Find
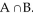 B.
B. 
A) {a, b, g, j, q, n, w}
B) {a, b, g, j, n, w}
C) {b, g}
D) {q}

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
Use the Venn diagram to find the requested set.
Find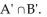
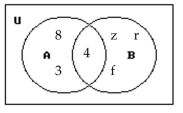
A) {8, 3, 4, z, r, f}
B) {4}
C) {8}
D)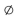
Find
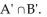

A) {8, 3, 4, z, r, f}
B) {4}
C) {8}
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false.
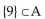

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
Let U = {a, l, i, t, e}, A = {l, i, t},B = {l, e}, C = {a, l, i, t, e}, and D = {a, e}. Find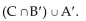
Let U = {a, l, i, t, e}, A = {l, i, t},B = {l, e}, C = {a, l, i, t, e}, and D = {a, e}. Find
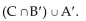

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
Use the Venn diagram to find the requested set.
Find A.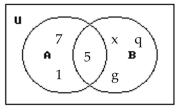
A) {5}
B)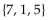
C)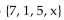
D)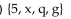
Find A.

A) {5}
B)
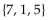
C)
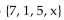
D)
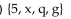

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false.
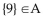
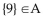

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
Use the Venn diagram to find the requested set.
Find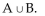
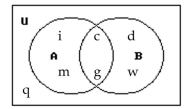
A) {d, c, g, i, m, w}
B) {d, c, g, i, q, m, w}
C) {q}
D) {c, g}
Find
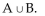

A) {d, c, g, i, m, w}
B) {d, c, g, i, q, m, w}
C) {q}
D) {c, g}

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Let A = {1, 3, 5, 7}; B = {5, 6, 7, 8}; C = {5, 8}; D = {2, 5, 8}; and U = {1, 2, 3, 4, 5, 6, 7, 8}. Determine whether the given statement
is true or false.
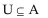
is true or false.
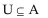

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
Let A = {6, 4, 1, {3, 0, 8}, {9}}. Determine whether the statement is true or false.
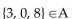
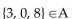

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
n(A) = 33, n(B) = 19, 19, n(A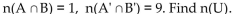
A) 60
B) 64
C) 51
D) 52
n(A) = 33, n(B) = 19, 19, n(A
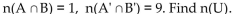
A) 60
B) 64
C) 51
D) 52

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
Provide an appropriate response.
One of the following is false; indicate by letter which one:
A)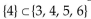
B)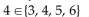
C)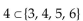
D)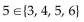
One of the following is false; indicate by letter which one:
A)
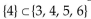
B)
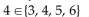
C)
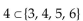
D)
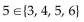

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set, and let 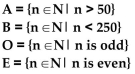
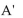
A) finite
B) infinite
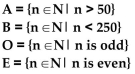
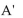
A) finite
B) infinite

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
Provide an appropriate response.
Which of the following is NOT a subset of the set owing is NOT a subset of the set {p, o,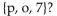
A) 7
B)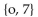
C)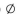
D)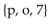
Which of the following is NOT a subset of the set owing is NOT a subset of the set {p, o,
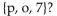
A) 7
B)
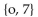
C)
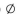
D)
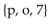

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set, and let 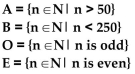
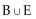
A) infinite
B) finite
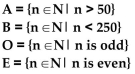
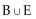
A) infinite
B) finite

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set, and let 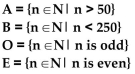

A) finite
B) infinite
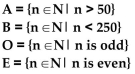

A) finite
B) infinite

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Provide an appropriate response.
In a group of 42 students, 22 take history, 17 take biology and 8 take both history and biology. How many students take biology, but not history?
A) 22
B) 5
C) 17
D) 9
In a group of 42 students, 22 take history, 17 take biology and 8 take both history and biology. How many students take biology, but not history?
A) 22
B) 5
C) 17
D) 9

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Provide an appropriate response.
Results of a survey of fifty students indicate that 30 like red jelly beans, 29 like green jelly beans, and 17 like both red and green jelly beans. How many of the students surveyed like neither red nor green jelly beans?
A) 13
B) 12
C) 8
D) 17
Results of a survey of fifty students indicate that 30 like red jelly beans, 29 like green jelly beans, and 17 like both red and green jelly beans. How many of the students surveyed like neither red nor green jelly beans?
A) 13
B) 12
C) 8
D) 17

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Provide an appropriate response.
A survey of residents in a certain town indicates 170 own a dehumidifier, 130 own a snow blower, and 80 own a dehumidifier and a snow blower. How many own a dehumidifier or a snow blower?
A) 80
B) 250
C) 170
D) 220
A survey of residents in a certain town indicates 170 own a dehumidifier, 130 own a snow blower, and 80 own a dehumidifier and a snow blower. How many own a dehumidifier or a snow blower?
A) 80
B) 250
C) 170
D) 220

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
Provide an appropriate response.
In a group of 42 students, 22 take history, 17 take biology and 8 take both history and biology. How many students take neither biology nor history?
A) 8
B) 5
C) 11
D) 22
In a group of 42 students, 22 take history, 17 take biology and 8 take both history and biology. How many students take neither biology nor history?
A) 8
B) 5
C) 11
D) 22

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Use the Venn diagram below to find the number of elements in the region. 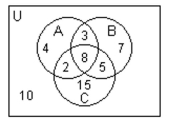
n(A)
A) 9
B) 12
C) 4
D) 17

n(A)
A) 9
B) 12
C) 4
D) 17

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Use the Venn diagram below to find the number of elements in the region. 
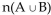
A) 29
B) 21
C) 11
D) 14

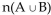
A) 29
B) 21
C) 11
D) 14

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Determine whether the given set is disjoint or not disjoint. Consider the set N of positive integers to be the universal set, and let 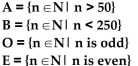
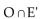
A) not disjoint
B) disjoint
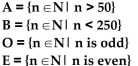
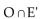
A) not disjoint
B) disjoint

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Use the addition principle for counting to solve the problem.
If n(B) = 24, n 24, n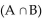 =5, and n, and n
=5, and n, and n 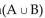 = 42, find n(A).
= 42, find n(A).
A) 24
B) 25
C) 23
D) 21
If n(B) = 24, n 24, n
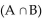 =5, and n, and n
=5, and n, and n 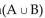 = 42, find n(A).
= 42, find n(A).A) 24
B) 25
C) 23
D) 21

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
Use the Venn diagram below to find the number of elements in the region. 
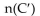
A) 29
B) 14
C) 24
D) 39

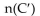
A) 29
B) 14
C) 24
D) 39

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Use the Venn diagram below to find the number of elements in the region. 
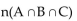
A) 44
B) 8
C) 16
D) 18

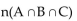
A) 44
B) 8
C) 16
D) 18

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
Provide an appropriate response.
A local television station sends out questionnaires to determine if viewers would rather see a documentary, an interview show, or reruns of a game show. There were 500 responses with the following results:
150 were interested in an interview show and a documentary, but not reruns.
20 were interested in an interview show and reruns but not a documentary
70 were interested in reruns but not an interview show.
120 were interested in an interview show but not a documentary.
50 were interested in a documentary and reruns.
30 were interested in an interview show and reruns.
40 were interested in none of the three.
How many are interested in exactly one kind of show?
A) 230
B) 220
C) 250
D) 240
A local television station sends out questionnaires to determine if viewers would rather see a documentary, an interview show, or reruns of a game show. There were 500 responses with the following results:
150 were interested in an interview show and a documentary, but not reruns.
20 were interested in an interview show and reruns but not a documentary
70 were interested in reruns but not an interview show.
120 were interested in an interview show but not a documentary.
50 were interested in a documentary and reruns.
30 were interested in an interview show and reruns.
40 were interested in none of the three.
How many are interested in exactly one kind of show?
A) 230
B) 220
C) 250
D) 240

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
At Southern States University (SSU) there are 399 students taking Finite Mathematics or Statistics. 238 are taking Finite Mathematics, 184 are taking Statistics, and 23 are taking both Finite Mathematics and Statistics. How
Many are taking Finite Mathematics but not Statistics?
A) 192
B) 215
C) 376
D) 161
At Southern States University (SSU) there are 399 students taking Finite Mathematics or Statistics. 238 are taking Finite Mathematics, 184 are taking Statistics, and 23 are taking both Finite Mathematics and Statistics. How
Many are taking Finite Mathematics but not Statistics?
A) 192
B) 215
C) 376
D) 161

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
In a marketing survey involving 1,000 randomly chosen people, it is found that 660 use brand P, 440 use brand
Q, and 220 use both brands. How many people in the survey use brand P and not brand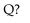
In a marketing survey involving 1,000 randomly chosen people, it is found that 660 use brand P, 440 use brand
Q, and 220 use both brands. How many people in the survey use brand P and not brand
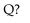

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Provide an appropriate response.
Mrs. Bollo's second grade class of thirty students conducted a pet ownership survey. Results of the survey indicate that 8 students own a cat, 15 students own a dog, and 5 students own both a cat and a dog. How many
Of the students surveyed own only a dog?
A) 10
B) 22
C) 15
D) 18
Mrs. Bollo's second grade class of thirty students conducted a pet ownership survey. Results of the survey indicate that 8 students own a cat, 15 students own a dog, and 5 students own both a cat and a dog. How many
Of the students surveyed own only a dog?
A) 10
B) 22
C) 15
D) 18

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Use the addition principle for counting to solve the problem.
If n(A) = 20, n 20, n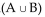 = 58, and n
= 58, and n 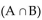 = 16, find n(B).
= 16, find n(B).
A) 54
B) 53
C) 55
D) 58
If n(A) = 20, n 20, n
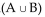 = 58, and n
= 58, and n 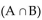 = 16, find n(B).
= 16, find n(B).A) 54
B) 53
C) 55
D) 58

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
Use the addition principle for counting to solve the problem.
If n(A) = 40, n(B) = 117 and d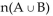 = 137, what is
= 137, what is 
A) 40
B) 10
C) 22
D) 20
If n(A) = 40, n(B) = 117 and d
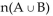 = 137, what is
= 137, what is 
A) 40
B) 10
C) 22
D) 20

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
Use a Venn Diagram and the given information to determine the number of elements in the indicated region.
At Southern States University SSU) there are 719 students taking Finite Mathematics or Statistics. 328 are taking Finite Mathematics, 476 are taking Statistics, and 85 are taking both Finite Mathematics and Statistics. How
Many are taking Statistics but not Finite Mathematics?
A) 243
B) 391
C) 158
D) 634
At Southern States University SSU) there are 719 students taking Finite Mathematics or Statistics. 328 are taking Finite Mathematics, 476 are taking Statistics, and 85 are taking both Finite Mathematics and Statistics. How
Many are taking Statistics but not Finite Mathematics?
A) 243
B) 391
C) 158
D) 634

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Use the addition principle for counting to solve the problem.
If n(A) = 5, n(B) = 11 and 11 and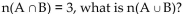
A) 14
B) 13
C) 11
D) 12
If n(A) = 5, n(B) = 11 and 11 and
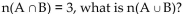
A) 14
B) 13
C) 11
D) 12

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Use the Venn diagram below to find the number of elements in the region. 
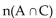
A) 2
B) 10
C) 18
D) 37

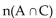
A) 2
B) 10
C) 18
D) 37

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Use the Venn diagram below to find the number of elements in the region. 
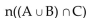
A) 14
B) 11
C) 33
D) 15

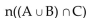
A) 14
B) 11
C) 33
D) 15

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Provide an appropriate response.
A restaurant offered pizza with 3 types of crusts and 7 different toppings. How many different types of pizzas could be offered?
A) 21
B) 9
C) 49
D) 10
E) 63
A restaurant offered pizza with 3 types of crusts and 7 different toppings. How many different types of pizzas could be offered?
A) 21
B) 9
C) 49
D) 10
E) 63

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate.
P6, 4
A) 360
B) 30
C) 2
D) 24
P6, 4
A) 360
B) 30
C) 2
D) 24

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Provide an appropriate response.
A test is composed of 4 multiple choice problems and 8 questions that can be answered true or false. Each
multiple choice problem has 4 choices. How many different response sheets are possible if only one choice is
marked for each question?
A test is composed of 4 multiple choice problems and 8 questions that can be answered true or false. Each
multiple choice problem has 4 choices. How many different response sheets are possible if only one choice is
marked for each question?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Provide an appropriate response.
Suppose there are 4 trains connecting town X to town Y and 6 roads connecting town Y to town Z. In how many ways can a person travel from X to Z via Y?
A) 10
B) 16
C) 12
D) 24
E) 36
Suppose there are 4 trains connecting town X to town Y and 6 roads connecting town Y to town Z. In how many ways can a person travel from X to Z via Y?
A) 10
B) 16
C) 12
D) 24
E) 36

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
Provide an appropriate response.
How many nine-digit ZIP code numbers are possible if the first digit cannot be a four and adjacent digits
cannot be the same?
How many nine-digit ZIP code numbers are possible if the first digit cannot be a four and adjacent digits
cannot be the same?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Provide an appropriate response.
A Super Duper Jean company has 3 designs that can be made with short or long length. There are 5 color patterns available. How many different types of jeans are available from this company?
A) 30
B) 10
C) 8
D) 15
E) 25
A Super Duper Jean company has 3 designs that can be made with short or long length. There are 5 color patterns available. How many different types of jeans are available from this company?
A) 30
B) 10
C) 8
D) 15
E) 25

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate.
6!
A) 1440
B) 120
C) 720
D) 360
6!
A) 1440
B) 120
C) 720
D) 360

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Provide an appropriate response.
In Virginia, each automobile license plate consists of a single digit followed by three letters, followed by three digits. How many distinct license plates can be formed if there are no restrictions on the digits or letters?
A) 17,575,600
B) 175,7560,000
C) 17,576
D) 175,760
E) 10,757,600
In Virginia, each automobile license plate consists of a single digit followed by three letters, followed by three digits. How many distinct license plates can be formed if there are no restrictions on the digits or letters?
A) 17,575,600
B) 175,7560,000
C) 17,576
D) 175,760
E) 10,757,600

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
Provide an appropriate response.
License plates are made using 3 letters followed by 3 digits. How many plates can be made if repetition of letters and digits is allowed?
A) 308,915,776
B) 1,757,600
C) 1,000,000
D) 175,760
E) 17,576,000
License plates are made using 3 letters followed by 3 digits. How many plates can be made if repetition of letters and digits is allowed?
A) 308,915,776
B) 1,757,600
C) 1,000,000
D) 175,760
E) 17,576,000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
Provide an appropriate response.
A combination lock on a suitcase has 5 wheels, each labeled with digits 1 to 8. How many 5-digit combination
lock codes are possible if no digit can be repeated?
A combination lock on a suitcase has 5 wheels, each labeled with digits 1 to 8. How many 5-digit combination
lock codes are possible if no digit can be repeated?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate.
P10, 2
A) 90
B) 45
C) 8
D) 19
P10, 2
A) 90
B) 45
C) 8
D) 19

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate.
1514!!
A) 7
B) 30
C) 14
D) 15
1514!!
A) 7
B) 30
C) 14
D) 15

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Provide an appropriate response.
The access code to a house's security system consists of five digits. How many different codes are available if each digit can be repeated?
A) 32
B) 45
C) 5
D) 100,000
E) 3125
The access code to a house's security system consists of five digits. How many different codes are available if each digit can be repeated?
A) 32
B) 45
C) 5
D) 100,000
E) 3125

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
Provide an appropriate response.
How many different five-letter code words are possible from the first ten letters of the alphabet if the first letter
cannot be a vowel and adjacent letters must be different.
How many different five-letter code words are possible from the first ten letters of the alphabet if the first letter
cannot be a vowel and adjacent letters must be different.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
Provide an appropriate response.
How many different sequences of 4 digits are possible if the first digit must be 3, 4, or 5 and if the sequence may not end in 000? Repetition of digits is allowed.
A) 5000
B) 2999
C) 1512
D) 2997
E) 2000
How many different sequences of 4 digits are possible if the first digit must be 3, 4, or 5 and if the sequence may not end in 000? Repetition of digits is allowed.
A) 5000
B) 2999
C) 1512
D) 2997
E) 2000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate.
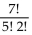
A) 7
B) 1
C) 42
D) 21
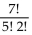
A) 7
B) 1
C) 42
D) 21

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate.
86!!
A)-86
B) 2!
C) 56
D) 8
86!!
A)-86
B) 2!
C) 56
D) 8

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate.
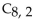
A) 720
B) 28
C) 1440
D) 4
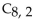
A) 720
B) 28
C) 1440
D) 4

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Provide an appropriate response.
A person purchasing a new car has several options: 6 interior color choices, 5 exterior color choices, 2 choices of
radios, and 5 choices of body styles. How many different cars are possible if one choice is made for each option?
A person purchasing a new car has several options: 6 interior color choices, 5 exterior color choices, 2 choices of
radios, and 5 choices of body styles. How many different cars are possible if one choice is made for each option?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Provide an appropriate response.
A coin that can turn up either heads (H) or tails (T) is flipped. If a head turns up on the first toss, a spinner that
can land on any of the first 7 natural numbers is spun. If a tail turns up, the coin is flipped a second time. What
are the different possible outcomes?
A coin that can turn up either heads (H) or tails (T) is flipped. If a head turns up on the first toss, a spinner that
can land on any of the first 7 natural numbers is spun. If a tail turns up, the coin is flipped a second time. What
are the different possible outcomes?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


