Deck 5: Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 5: Integration
1
Use graphical methods to solve the linear programming problem.
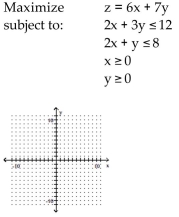
A) Maximum of 32 when x = 3 and y = 2
B) Maximum of 24 when x = 4 and y = 0
C) Maximum of 52 when x = 4 and y = 4
D) Maximum of 32 when x = 2 and y = 3

A) Maximum of 32 when x = 3 and y = 2
B) Maximum of 24 when x = 4 and y = 0
C) Maximum of 52 when x = 4 and y = 4
D) Maximum of 32 when x = 2 and y = 3
Maximum of 32 when x = 3 and y = 2
2
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or
unbounded.
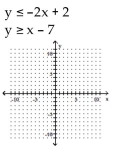
A)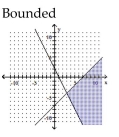
B)
C)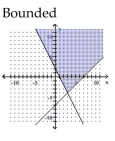
D)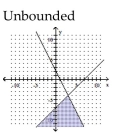
unbounded.

A)

B)

C)

D)


3
Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the
maximum profit occurs for the given objective function.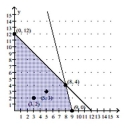
P = 5x + y
A) Max P = 45 at x = 9 and y = 0, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
B) Max P = 44 at x = 8 and y = 4, at x = 0 and y = 12, and at every point on the line segment joining the preceding two points.
C) Max P = 44 at x = 8 and y = 4
D) Max P = 45 at x = 9 and y = 0
maximum profit occurs for the given objective function.

P = 5x + y
A) Max P = 45 at x = 9 and y = 0, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
B) Max P = 44 at x = 8 and y = 4, at x = 0 and y = 12, and at every point on the line segment joining the preceding two points.
C) Max P = 44 at x = 8 and y = 4
D) Max P = 45 at x = 9 and y = 0
Max P = 45 at x = 9 and y = 0
4
Graph the inequality.
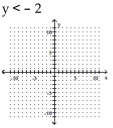
A)
B)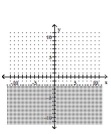
C)
D)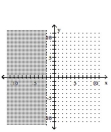

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
Define the variable(s) and translate the sentence into an inequality.
Enrollment is below 8000 students.
A) Let e = student enrollment; e < 8000
B)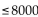
C) Let e = student enrollment; e > 8000
D)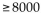
Enrollment is below 8000 students.
A) Let e = student enrollment; e < 8000
B)
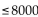
C) Let e = student enrollment; e > 8000
D)
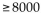

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the inequality.
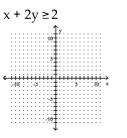
A)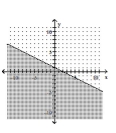
B)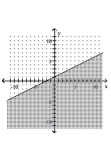
C)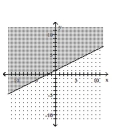
D)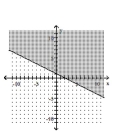

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem.
Company A rents copiers for a monthly charge of $300 plus 10 cents per copy. Company B rents copiers for a monthly charge of $600 plus 5 cents per copy. What is the number of copies above which Company A's charges
Are the higher of the two?
A) 12,000 copies
B) 3000 copies
C) 6000 copies
D) 6100 copies
Company A rents copiers for a monthly charge of $300 plus 10 cents per copy. Company B rents copiers for a monthly charge of $600 plus 5 cents per copy. What is the number of copies above which Company A's charges
Are the higher of the two?
A) 12,000 copies
B) 3000 copies
C) 6000 copies
D) 6100 copies

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
Define the variable(s) and translate the sentence into an inequality.
Sales of wheat bread are at least $2000 greater than sales of white bread.
A)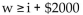
B)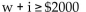
C)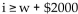
D)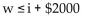
Sales of wheat bread are at least $2000 greater than sales of white bread.
A)
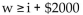
B)
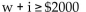
C)
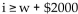
D)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the problem.
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A small accounting firm
prepares tax returns for two types of customers: individuals and small businesses. Data is collected during an
interview. A computer system is used to produce the tax return. It takes 2.5 hours to enter data into the
computer for an individual tax return and 3 hours to enter data for a small business tax return. There is a
maximum of 40 hours per week for data entry. It takes 20 minutes for the computer to process an individual tax
return and 30 minutes to process a small business tax return. The computer is available for a maximum of 900
minutes per week. The accounting firm makes a profit of $125 on each individual tax return processed and a
profit of $210 on each small business tax return processed. How many of each type of tax return should the firm
schedule each week in order to maximize its profit? (Let x1 equal the number of individual tax returns and x2
the number of small business tax returns.)
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A small accounting firm
prepares tax returns for two types of customers: individuals and small businesses. Data is collected during an
interview. A computer system is used to produce the tax return. It takes 2.5 hours to enter data into the
computer for an individual tax return and 3 hours to enter data for a small business tax return. There is a
maximum of 40 hours per week for data entry. It takes 20 minutes for the computer to process an individual tax
return and 30 minutes to process a small business tax return. The computer is available for a maximum of 900
minutes per week. The accounting firm makes a profit of $125 on each individual tax return processed and a
profit of $210 on each small business tax return processed. How many of each type of tax return should the firm
schedule each week in order to maximize its profit? (Let x1 equal the number of individual tax returns and x2
the number of small business tax returns.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the problem.
Formulate the following problem as a linear programming problem (DO NOT SOLVE).A company which
produces three kinds of spaghetti sauce has two plants. The East plant produces 3,500 jars of plain sauce, 6,500
jars of sauce with mushrooms, and 3,000 jars of hot spicy sauce per day. The West plant produces 2,500 jars of
plain sauce, 2,000 jars of sauce with mushrooms, and 1,500 jars of hot spicy sauce per day. The cost to operate
the East plant is $8,500 per day and the cost to operate the West plant is $9,500 per day. How many days should
each plant operate to minimize cost and to fill an order for at least 8,000 jars of plain sauce, 9,000 jars of sauce
with mushrooms, and 6,000 jars of hot spicy sauce? (Let x1 equal the number of days East plant should operate
and x2 the number of days West plant should operate.)
Formulate the following problem as a linear programming problem (DO NOT SOLVE).A company which
produces three kinds of spaghetti sauce has two plants. The East plant produces 3,500 jars of plain sauce, 6,500
jars of sauce with mushrooms, and 3,000 jars of hot spicy sauce per day. The West plant produces 2,500 jars of
plain sauce, 2,000 jars of sauce with mushrooms, and 1,500 jars of hot spicy sauce per day. The cost to operate
the East plant is $8,500 per day and the cost to operate the West plant is $9,500 per day. How many days should
each plant operate to minimize cost and to fill an order for at least 8,000 jars of plain sauce, 9,000 jars of sauce
with mushrooms, and 6,000 jars of hot spicy sauce? (Let x1 equal the number of days East plant should operate
and x2 the number of days West plant should operate.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the inequality.
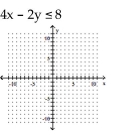
A)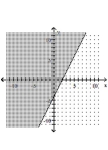
B)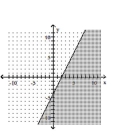
C)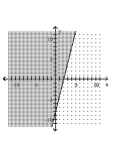
D)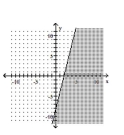

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or
unbounded.
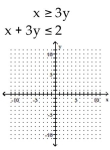
A)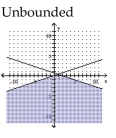
B)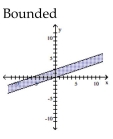
C)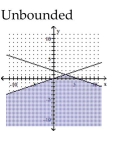
D)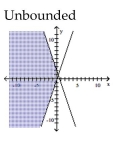
unbounded.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the inequality.
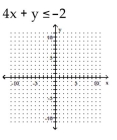
A)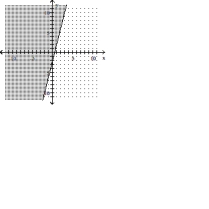
B)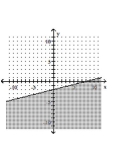
C)
D)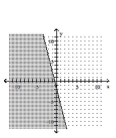

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or
unbounded.
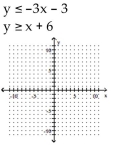
A)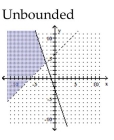
B)
C)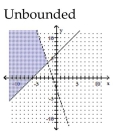
D)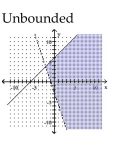
unbounded.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the problem.
Jim has gotten scores of 78 and 69 on his first two tests. What score must he get on his third test to keep an average of 70 or greater?
A) At least 63
B) At least 62
C) At least 72.3
D) At least 73.5
Jim has gotten scores of 78 and 69 on his first two tests. What score must he get on his third test to keep an average of 70 or greater?
A) At least 63
B) At least 62
C) At least 72.3
D) At least 73.5

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or
unbounded.
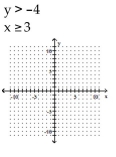
A)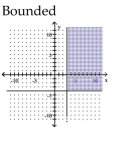
B)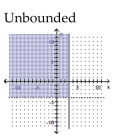
C)
D)
unbounded.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the
maximum profit occurs for the given objective function.
P = x + y
A) Max P = 8 at x = 5 and y = 3
B) Max P = 5 at x = 3 and y = 2
C) Max P = 9 at x = 9 and y = 0, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
D) Max P = 12 at x = 0 and y = 12, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
maximum profit occurs for the given objective function.

P = x + y
A) Max P = 8 at x = 5 and y = 3
B) Max P = 5 at x = 3 and y = 2
C) Max P = 9 at x = 9 and y = 0, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
D) Max P = 12 at x = 0 and y = 12, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or
unbounded.
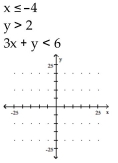
A)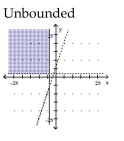
B)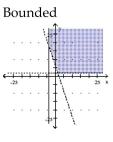
C)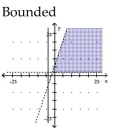
D)
unbounded.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
Provide an appropriate response.
Find the coordinates of the corner points of the solution region for: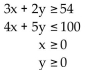
Find the coordinates of the corner points of the solution region for:
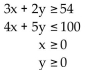

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.
A salesperson has two job offers. Company A offers a weekly salary of $180 plus commission of 6% of sales. Company B offers a weekly salary of $360 plus commission of 3% of sales. What is the amount of sales above
Which Company A's offer is the better of the two?
A) $12,000
B) $3000
C) $6000
D) $6100
A salesperson has two job offers. Company A offers a weekly salary of $180 plus commission of 6% of sales. Company B offers a weekly salary of $360 plus commission of 3% of sales. What is the amount of sales above
Which Company A's offer is the better of the two?
A) $12,000
B) $3000
C) $6000
D) $6100

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the problem.
The Southern States Ring Company designs and sells two types of rings: the brass and the aluminum. They can
produce up to 24 rings each day using up to 60 total man-hours of labor per day. It takes 3 man-hours to make
one brass ring and 2 man-hours to make one aluminum ring. How many of each type of ring should be made
daily to maximize the company's profit, if the profit on a brass ring is $40 and on an aluminum ring is $35?
The Southern States Ring Company designs and sells two types of rings: the brass and the aluminum. They can
produce up to 24 rings each day using up to 60 total man-hours of labor per day. It takes 3 man-hours to make
one brass ring and 2 man-hours to make one aluminum ring. How many of each type of ring should be made
daily to maximize the company's profit, if the profit on a brass ring is $40 and on an aluminum ring is $35?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.
The Old-World Class Ring Company designs and sells two types of rings: the BRASS and the GOLD. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one
BRASS ring and 2 man-hours to make one GOLD ring. How many of each type of ring should be made daily to
Maximize the company's profit, if the profit on a BRASS ring is $40 and on an GOLD ring is $30?
A) 14 BRASS and 10 GOLD
B) 12 BRASS and 12 GOLD
C) 14 BRASS and 14 GOLD
D) 10 BRASS and 14 GOLD
The Old-World Class Ring Company designs and sells two types of rings: the BRASS and the GOLD. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one
BRASS ring and 2 man-hours to make one GOLD ring. How many of each type of ring should be made daily to
Maximize the company's profit, if the profit on a BRASS ring is $40 and on an GOLD ring is $30?
A) 14 BRASS and 10 GOLD
B) 12 BRASS and 12 GOLD
C) 14 BRASS and 14 GOLD
D) 10 BRASS and 14 GOLD

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Give the mathematical formulation of the linear programming problem. Graph the feasible region described by the
constraints and find the corner points. Do not attempt to solve.
A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The monthly salary
of a counselor is $2400 and the monthly salary of an aide is $1100. The camp can accommodate up to 45 staff
members and needs at least 30 to run properly. They must have at least 10 aides, and at most twice as many
aides as counselors. How many counselors and how many aides should the camp hire to minimize cost?
constraints and find the corner points. Do not attempt to solve.
A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The monthly salary
of a counselor is $2400 and the monthly salary of an aide is $1100. The camp can accommodate up to 45 staff
members and needs at least 30 to run properly. They must have at least 10 aides, and at most twice as many
aides as counselors. How many counselors and how many aides should the camp hire to minimize cost?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
Provide an appropriate response.
The corner points for the bounded feasible region determined by the system of inequalities: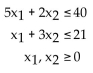 are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:
P = 5x1 + 5x2
The corner points for the bounded feasible region determined by the system of inequalities:
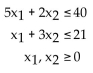 are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:P = 5x1 + 5x2

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
Use graphical methods to solve the linear programming problem.
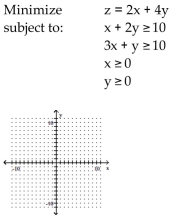
A) Minimum of 0 when x = 0 and y = 0
B) Minimum of 20 when x = 10 and y = 0
C) Minimum of 20 when x = 2 and y = 4
D) Minimum of 20 when x = 2 and y = 4, as well as when x = 10 and y = 0, and all points in between

A) Minimum of 0 when x = 0 and y = 0
B) Minimum of 20 when x = 10 and y = 0
C) Minimum of 20 when x = 2 and y = 4
D) Minimum of 20 when x = 2 and y = 4, as well as when x = 10 and y = 0, and all points in between

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
Provide an appropriate response.
Refer to the following system of linear inequalities associated with a linear programming problem: (A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(B) Determine the number of basic variables associated with this system.
Refer to the following system of linear inequalities associated with a linear programming problem:
 (A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.(B) Determine the number of basic variables associated with this system.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the problem.
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company
produces two types of machine dies, part A and part B. Part A requires 6 hours of casting time and 4 hours of
firing time. Part B requires 8 hours of casting time and 3 hours of firing time. The maximum number of hours
per week available for casting and firing are 85 and 70, respectively. The company makes a $2.00 profit on each
part A that it produces, and a $6.00 profit on each part B that it produces. How many of each type should the
company produce each week in order to maximize its profit? (Let x1 equal the number of A parts and x2 equal
the number of B parts produced each week.)
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company
produces two types of machine dies, part A and part B. Part A requires 6 hours of casting time and 4 hours of
firing time. Part B requires 8 hours of casting time and 3 hours of firing time. The maximum number of hours
per week available for casting and firing are 85 and 70, respectively. The company makes a $2.00 profit on each
part A that it produces, and a $6.00 profit on each part B that it produces. How many of each type should the
company produce each week in order to maximize its profit? (Let x1 equal the number of A parts and x2 equal
the number of B parts produced each week.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
Use graphical methods to solve the linear programming problem.
A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100. The camp can accommodate
Up to 45 staff members and needs at least 30 to run properly. They must have at least 10 aides, and may have
Up to 3 aides for every 2 counselors. How many counselors and how many aides should the camp hire to
Minimize cost?
A) 27 counselors and 18 aides
B) 18 counselors and 12 aides
C) 35 counselors and 10 aides
D) 12 counselors and 18 aides
A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100. The camp can accommodate
Up to 45 staff members and needs at least 30 to run properly. They must have at least 10 aides, and may have
Up to 3 aides for every 2 counselors. How many counselors and how many aides should the camp hire to
Minimize cost?
A) 27 counselors and 18 aides
B) 18 counselors and 12 aides
C) 35 counselors and 10 aides
D) 12 counselors and 18 aides

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
Give the mathematical formulation of the linear programming problem. Graph the feasible region described by the
constraints and find the corner points. Do not attempt to solve.
Suppose an horse feed to be mixed from soybean meal and oats must contain at least 200 lb of protein and 40 lb
of fat. Each sack of soybean meal costs $20 and contains 60 lb of protein and 10 lb of fat. Each sack of oats costs
$10 and contains 20 lb of protein and 5 lb of fat. How many sacks of each should be used to satisfy the minimum
requirements at minimum cost?
constraints and find the corner points. Do not attempt to solve.
Suppose an horse feed to be mixed from soybean meal and oats must contain at least 200 lb of protein and 40 lb
of fat. Each sack of soybean meal costs $20 and contains 60 lb of protein and 10 lb of fat. Each sack of oats costs
$10 and contains 20 lb of protein and 5 lb of fat. How many sacks of each should be used to satisfy the minimum
requirements at minimum cost?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A dietitian can purchase
an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. Each ounce of chicken contains 13 units of
protein and 24 units of carbohydrates. Each ounce of potatoes contains 5 units of protein and 35 units of
carbohydrates. The minimum daily requirements for the patients under the dietitian's care are 45 units of
protein and 58 units of carbohydrates. How many ounces of each type of food should the dietitian purchase for
each patient so as to minimize costs and at the same time insure the minimum daily requirements of protein
and carbohydrates? (Let x1 equal the number of ounces of chicken and x2 the number of ounces of potatoes
purchased per patient.)
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A dietitian can purchase
an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. Each ounce of chicken contains 13 units of
protein and 24 units of carbohydrates. Each ounce of potatoes contains 5 units of protein and 35 units of
carbohydrates. The minimum daily requirements for the patients under the dietitian's care are 45 units of
protein and 58 units of carbohydrates. How many ounces of each type of food should the dietitian purchase for
each patient so as to minimize costs and at the same time insure the minimum daily requirements of protein
and carbohydrates? (Let x1 equal the number of ounces of chicken and x2 the number of ounces of potatoes
purchased per patient.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
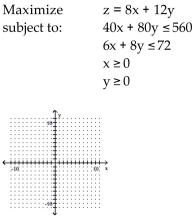
Use graphical methods to solve the linear programming problem.
Suppose an horse feed to be mixed from soybean meal and oats must contain at least 100 lb of protein, 20 lb of fat, and 9 lb of mineral ash. Each 100-lb sack of soybean meal costs $20 and contains 50 lb of protein, 10 lb of fat,
And 8 lb of mineral ash. Each 100-lb sack of oats costs $10 and contains 20 lb of protein, 5 lb of fat, and 1 lb of
Mineral ash. How many sacks of each should be used to satisfy the minimum requirements at minimum cost?
A) 2 sacks of soybeans and 0 sacks of oats
B)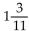 sacks of s sacks of soybeans and nd
sacks of s sacks of soybeans and nd 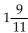 sac sacks of oats
sac sacks of oats
C)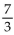 sacks of s sacks of soybeans and
sacks of s sacks of soybeans and 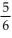 sac sacks of oats
sac sacks of oats
D) 0 sacks of soybeans and 2 sacks of oats
Suppose an horse feed to be mixed from soybean meal and oats must contain at least 100 lb of protein, 20 lb of fat, and 9 lb of mineral ash. Each 100-lb sack of soybean meal costs $20 and contains 50 lb of protein, 10 lb of fat,
And 8 lb of mineral ash. Each 100-lb sack of oats costs $10 and contains 20 lb of protein, 5 lb of fat, and 1 lb of
Mineral ash. How many sacks of each should be used to satisfy the minimum requirements at minimum cost?
A) 2 sacks of soybeans and 0 sacks of oats
B)
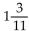 sacks of s sacks of soybeans and nd
sacks of s sacks of soybeans and nd 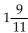 sac sacks of oats
sac sacks of oatsC)
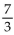 sacks of s sacks of soybeans and
sacks of s sacks of soybeans and 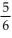 sac sacks of oats
sac sacks of oatsD) 0 sacks of soybeans and 2 sacks of oats

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
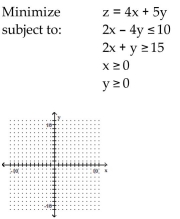
Use graphical methods to solve the linear programming problem.
A) Minimum of 33 when x = 7 and y = 1
B) Minimum of 39 when x = 1 and y = 7
C) Minimum of 20 when x = 5 and y = 0
D) Minimum of 75 when x = 0 and y = 15

A) Minimum of 33 when x = 7 and y = 1
B) Minimum of 39 when x = 1 and y = 7
C) Minimum of 20 when x = 5 and y = 0
D) Minimum of 75 when x = 0 and y = 15

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the problem.
A vineyard produces two special wines a white, and a red. A bottle of the white wine requires 14 pounds of
grapes and 1 hour of processing time. A bottle of red wine requires 25 pounds of grapes and 2 hours of
processing time. The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing time to
the production of these wines. A bottle of the white wine sells for $11.00, while a bottle of the red wine sells for
$20.00. How many bottles of each type should the vineyard produce in order to maximize gross sales? (Solve
using the geometric method.)
A vineyard produces two special wines a white, and a red. A bottle of the white wine requires 14 pounds of
grapes and 1 hour of processing time. A bottle of red wine requires 25 pounds of grapes and 2 hours of
processing time. The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing time to
the production of these wines. A bottle of the white wine sells for $11.00, while a bottle of the red wine sells for
$20.00. How many bottles of each type should the vineyard produce in order to maximize gross sales? (Solve
using the geometric method.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
Use graphical methods to solve the linear programming problem.
A) Maximum of 100 when x = 8 and y = 3
B) Maximum of 96 when x = 9 and y = 2
C) Maximum of 120 when x = 3 and y = 8
D) Maximum of 92 when x = 4 and y = 5

A) Maximum of 100 when x = 8 and y = 3
B) Maximum of 96 when x = 9 and y = 2
C) Maximum of 120 when x = 3 and y = 8
D) Maximum of 92 when x = 4 and y = 5

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
Provide an appropriate response.
Using a graphing calculator as needed, maximize P = 310x1 + 470x2 subject to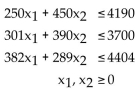 Give the answer to two decimal places.
Give the answer to two decimal places.
Using a graphing calculator as needed, maximize P = 310x1 + 470x2 subject to
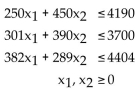 Give the answer to two decimal places.
Give the answer to two decimal places.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
Provide an appropriate response.
Solve the following linear programming problem by determining the feasible region on the graph below and testing the
corner points: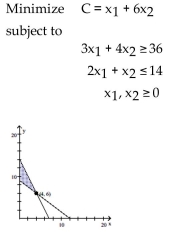 x1 is shown on the x-axis and x2 on the y-axis.
x1 is shown on the x-axis and x2 on the y-axis.
Solve the following linear programming problem by determining the feasible region on the graph below and testing the
corner points:
 x1 is shown on the x-axis and x2 on the y-axis.
x1 is shown on the x-axis and x2 on the y-axis.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Provide an appropriate response.
The corner points for the bounded feasible region determined by the system of inequalities: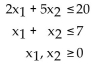 are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:
P(x) = 3x1 + 7x2
The corner points for the bounded feasible region determined by the system of inequalities:
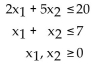 are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:P(x) = 3x1 + 7x2

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
Provide an appropriate response.
Using a graphing calculator as needed, maximize P = 524x1 + 479x2 subject to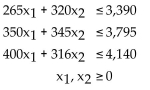 Give the answer to two decimal places.
Give the answer to two decimal places.
Using a graphing calculator as needed, maximize P = 524x1 + 479x2 subject to
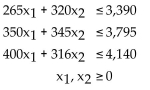 Give the answer to two decimal places.
Give the answer to two decimal places.
Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


