Deck 9: Systems of Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/139
Play
Full screen (f)
Deck 9: Systems of Linear Equations
1
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
2x - 3y = 9 6x - 9y = 36
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
2x - 3y = 9 6x - 9y = 36
A) infinite number of solutions
B) no solution
C) one solution
no solution
2
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -4 x + y = 8
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -4 x + y = 8
A) infinite number of solutions
B) no solution
C) one solution
no solution
3
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
9x = 6y + 3 9x = 6y - 5
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
9x = 6y + 3 9x = 6y - 5
A) infinite number of solutions
B) no solution
C) one solution
no solution
4
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
4x + 6y = 44 4x + 2y = 52
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
4x + 6y = 44 4x + 2y = 52
A) infinite number of solutions
B) no solution
C) one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
5
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -50
Y = 9x
A) one solution
B) no solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -50
Y = 9x
A) one solution
B) no solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
6
Determine if the following ordered pair satisfies the system of linear equations.
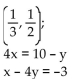
A) Yes
B) No
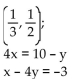
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
7
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
6x - 4y = 2 -12x + 8y = -8
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
6x - 4y = 2 -12x + 8y = -8
A) infinite number of solutions
B) no solution
C) one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the system of linear equations as consistent, inconsistent, or dependent. State whether the system has exactly one
solution, no solution, or an infinite number of solutions.
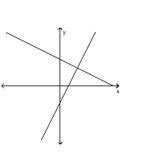
A) inconsistent-no solution
B) dependent-infinite number of solutions
C) consistent-one solution
solution, no solution, or an infinite number of solutions.

A) inconsistent-no solution
B) dependent-infinite number of solutions
C) consistent-one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
9
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
5x - 7y = -9 5x - 7y = 9
A) infinite number of solutions
B) one solution
C) no solution
has exactly one solution, no solution, or an infinite number of solutions.
5x - 7y = -9 5x - 7y = 9
A) infinite number of solutions
B) one solution
C) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
10
Identify the system of linear equations as consistent, inconsistent, or dependent. State whether the system has exactly one
solution, no solution, or an infinite number of solutions.
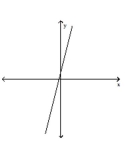
A) consistent-one solution
B) inconsistent-no solution
C) dependent-infinite number of solutions
solution, no solution, or an infinite number of solutions.

A) consistent-one solution
B) inconsistent-no solution
C) dependent-infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
11
Identify the system of linear equations as consistent, inconsistent, or dependent. State whether the system has exactly one
solution, no solution, or an infinite number of solutions.
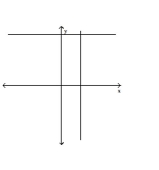
A) inconsistent-no solution
B) dependent-infinite number of solutions
C) consistent-one solution
solution, no solution, or an infinite number of solutions.

A) inconsistent-no solution
B) dependent-infinite number of solutions
C) consistent-one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
12
Determine if the following ordered pair satisfies the system of linear equations.
(-6, -2) 4x + y = -22
3x + 4y = -10
A) Yes
B) No
(-6, -2) 4x + y = -22
3x + 4y = -10
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
13
Identify the system of linear equations as consistent, inconsistent, or dependent. State whether the system has exactly one
solution, no solution, or an infinite number of solutions.
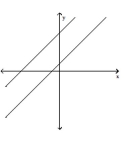
A) consistent-one solution
B) dependent-infinite number of solutions
C) inconsistent-no solution
solution, no solution, or an infinite number of solutions.

A) consistent-one solution
B) dependent-infinite number of solutions
C) inconsistent-no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
14
Determine if the following ordered pair satisfies the system of linear equations.
(6, 2) 2x = -10 - y
3x = -14 - 2y
A) Yes
B) No
(6, 2) 2x = -10 - y
3x = -14 - 2y
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
15
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -1 x - y = 11
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
x + y = -1 x - y = 11
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
16
Determine if the following ordered pair satisfies the system of linear equations.
(-2, 6) y = 4x + 14
Y = -3x
A) Yes
B) No
(-2, 6) y = 4x + 14
Y = -3x
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
17
Determine if the following ordered pair satisfies the system of linear equations.
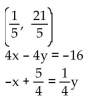
A) Yes
B) No
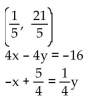
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
18
Determine if the following ordered pair satisfies the system of linear equations.
(-4, -3) x + y = 1
X - y = 7
A) Yes
B) No
(-4, -3) x + y = 1
X - y = 7
A) Yes
B) No

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
19
Identify the system of linear equations as consistent, inconsistent, or dependent. State whether the system has exactly one
solution, no solution, or an infinite number of solutions.
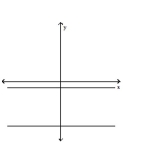
A) dependent-infinite number of solutions
B) consistent-one solution
C) inconsistent-no solution
solution, no solution, or an infinite number of solutions.

A) dependent-infinite number of solutions
B) consistent-one solution
C) inconsistent-no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
20
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
y = x - 6 x - 5y = 30
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
y = x - 6 x - 5y = 30
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
21
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
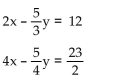
A) one solution
B) no solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
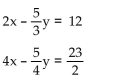
A) one solution
B) no solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
22
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
y - 4x = 5 5y = 20x + 25
A) one solution
B) no solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
y - 4x = 5 5y = 20x + 25
A) one solution
B) no solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
23
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
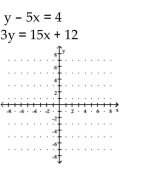
A) (-1.5, -1)
B) (1, 1)
C) dependent
D) inconsistent

A) (-1.5, -1)
B) (1, 1)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
24
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
5x + y = 0 4x - 2y = -14
A) no solution
B) infinite number of solutions
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
5x + y = 0 4x - 2y = -14
A) no solution
B) infinite number of solutions
C) one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
25
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
4x - 2y = -18 x = -4y
A) infinite number of solutions
B) one solution
C) no solution
has exactly one solution, no solution, or an infinite number of solutions.
4x - 2y = -18 x = -4y
A) infinite number of solutions
B) one solution
C) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
26
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
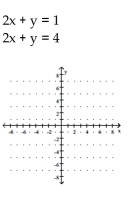
A) (2, 0)
B) 12 , 0
C) dependent
D) inconsistent

A) (2, 0)
B) 12 , 0
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
27
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
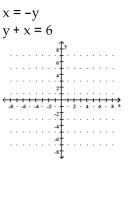
A) (1, 1)
B) (1, 5)
C) dependent
D) inconsistent

A) (1, 1)
B) (1, 5)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
28
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
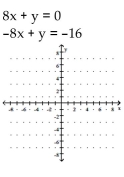
A) (1, -8)
B) (-1, 8)
C) (-1, -8)
D) (1, 16)

A) (1, -8)
B) (-1, 8)
C) (-1, -8)
D) (1, 16)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
29
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
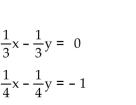
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
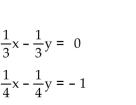
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
30
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
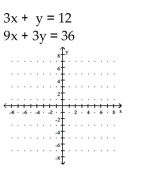
A) (0, 12)
B) (5, -3)
C) dependent
D) inconsistent

A) (0, 12)
B) (5, -3)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
31
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
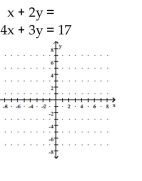
A) (3, 2)
B) (2, 3)
C) dependent
D) inconsistent

A) (3, 2)
B) (2, 3)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
32
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
y = 3x - 1 5y + 20x = 65
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
y = 3x - 1 5y + 20x = 65
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
33
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
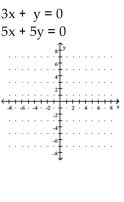
A) (0,0)
B) (4, 5)
C) dependent
D) inconsistent

A) (0,0)
B) (4, 5)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
34
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
-7y = x + 34 2x + 6y = -36
A) infinite number of solutions
B) no solution
C) one solution
has exactly one solution, no solution, or an infinite number of solutions.
-7y = x + 34 2x + 6y = -36
A) infinite number of solutions
B) no solution
C) one solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
35
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
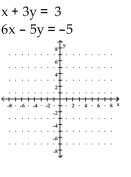
A) (0, 0)
B) (1, 0)
C) (1, 1)
D) (0, 1)

A) (0, 0)
B) (1, 0)
C) (1, 1)
D) (0, 1)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
36
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
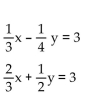
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
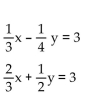
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
37
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
2y = x + 24 2x + 4y = 0
A) no solution
B) one solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
2y = x + 24 2x + 4y = 0
A) no solution
B) one solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
38
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
2x + y = 8 8x + 4y = 32
A) one solution
B) no solution
C) infinite number of solutions
has exactly one solution, no solution, or an infinite number of solutions.
2x + y = 8 8x + 4y = 32
A) one solution
B) no solution
C) infinite number of solutions

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
39
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
-3x - 9y = -10 5x + 15y = 0
A) one solution
B) infinite number of solutions
C) no solution
has exactly one solution, no solution, or an infinite number of solutions.
-3x - 9y = -10 5x + 15y = 0
A) one solution
B) infinite number of solutions
C) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
40
Express each equation in slope-intercept form. Without graphing the equations, state whether the system of equations
has exactly one solution, no solution, or an infinite number of solutions.
y y == 47x x -- 2 3
A) infinite number of solutions
B) one solution
C) no solution
has exactly one solution, no solution, or an infinite number of solutions.
y y == 47x x -- 2 3
A) infinite number of solutions
B) one solution
C) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
41
Find the solution by graphing the system of equations.
The Family Fine Arts Center charges $23 per adult and $12 per senior citizen for its performances. On a recent weekend evening when 446 people paid admission, the total receipts were $6485. We can represent this situation
With the system of equations
A + s = 446
23a + 12s = 6485
With a representing the adults who attended and s representing the senior citizens who attended. How many who paid
Were senior citizens?
A) 103 senior citizens
B) 253 senior citizens
C) 193 senior citizens
D) 343 senior citizens
The Family Fine Arts Center charges $23 per adult and $12 per senior citizen for its performances. On a recent weekend evening when 446 people paid admission, the total receipts were $6485. We can represent this situation
With the system of equations
A + s = 446
23a + 12s = 6485
With a representing the adults who attended and s representing the senior citizens who attended. How many who paid
Were senior citizens?
A) 103 senior citizens
B) 253 senior citizens
C) 193 senior citizens
D) 343 senior citizens

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
42
Find the solution to the system of equations by substitution.
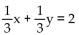 x - y = -4
x - y = -4
A) (0, 6)
B) (-1, 6)
C) (1, 5)
D) no solution
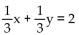 x - y = -4
x - y = -4A) (0, 6)
B) (-1, 6)
C) (1, 5)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
43
Find the solution to the system of equations by substitution.
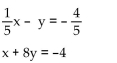
A) (4, 0)
B) (0, 4)
C) (-4, 0)
D) (0, -4)
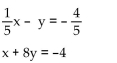
A) (4, 0)
B) (0, 4)
C) (-4, 0)
D) (0, -4)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
44
Find the solution to the system of equations by substitution.
y - 5x = 3 2y = 10x + 6
A) (-1.5, -1)
B) (1, 1)
C) infinite number of solutions
D) no solution
y - 5x = 3 2y = 10x + 6
A) (-1.5, -1)
B) (1, 1)
C) infinite number of solutions
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
45
Determine the solution to the system of linear equations graphically. If the system is dependent or inconsistent, so state.
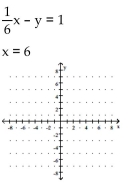
A) (6, 1)
B) (6, 0)
C) 6, 56
D) (0, 6)

A) (6, 1)
B) (6, 0)
C) 6, 56
D) (0, 6)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
46
Find the solution to the system of equations by substitution.
x + y = -2 x - y = 12
A) 5, - 7
B) 2, - 7
C) 2, 5
D) 5, 7
x + y = -2 x - y = 12
A) 5, - 7
B) 2, - 7
C) 2, 5
D) 5, 7

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
47
Find the solution to the system of equations by substitution.
x = -y y + x = 6
A) (1, 1)
B) (1, 5)
C) infinite number of solutions
D) no solution
x = -y y + x = 6
A) (1, 1)
B) (1, 5)
C) infinite number of solutions
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
48
Find the solution by graphing the system of equations.
A shopkeeper ordered a total of 30 pounds of cashews and peanuts. He ordered 20 fewer pounds of cashews than peanuts. We can represent this situation with the system of equations
C + p = 30
P - c = 20
Where p represents the pounds of peanuts and c represents the pounds of cashews. How many pounds of peanuts did
He order?
A) 25 lb
B) 15 lb
C) 5 lb
D) 10 lb
A shopkeeper ordered a total of 30 pounds of cashews and peanuts. He ordered 20 fewer pounds of cashews than peanuts. We can represent this situation with the system of equations
C + p = 30
P - c = 20
Where p represents the pounds of peanuts and c represents the pounds of cashews. How many pounds of peanuts did
He order?
A) 25 lb
B) 15 lb
C) 5 lb
D) 10 lb

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
49
Find the solution to the system of equations by substitution.
9x + y = 0 -9x + y = -18
A) (1, 18)
B) (1, -9)
C) (-1, 9)
D) (-1, -9)
9x + y = 0 -9x + y = -18
A) (1, 18)
B) (1, -9)
C) (-1, 9)
D) (-1, -9)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
50
Find the solution to the system of equations by substitution.
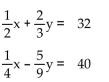
A) (100, -27)
B) (-100, -27)
C) (100, 27)
D) (-100, 27)
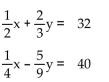
A) (100, -27)
B) (-100, -27)
C) (100, 27)
D) (-100, 27)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
51
Find the solution by graphing the system of equations.
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 6 slices of pizza and 5 soft drinks for $28.45. The second group bought 5 slices of pizza and 5 soft drinks for $
25)10. We can represent this situation with the system of equations
6p + 5s = 28.45
5p + 5s = 25.10
Where p is the cost of a slice of pizza and s is the cost of a soft drink. Determine the cost of one slice of pizza.
A) $1.67 per slice of pizza
B) $3.35 per slice of pizza
C) $2.17 per slice of pizza
D) $2.85 per slice of pizza
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 6 slices of pizza and 5 soft drinks for $28.45. The second group bought 5 slices of pizza and 5 soft drinks for $
25)10. We can represent this situation with the system of equations
6p + 5s = 28.45
5p + 5s = 25.10
Where p is the cost of a slice of pizza and s is the cost of a soft drink. Determine the cost of one slice of pizza.
A) $1.67 per slice of pizza
B) $3.35 per slice of pizza
C) $2.17 per slice of pizza
D) $2.85 per slice of pizza

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
52
Find the solution to the system of equations by substitution.
x + 9y = 9 8x - 5y = -5
A) (0, 1)
B) (1, 1)
C) (1, 0)
D) (0, 0)
x + 9y = 9 8x - 5y = -5
A) (0, 1)
B) (1, 1)
C) (1, 0)
D) (0, 0)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
53
Find the solution to the system of equations by substitution.
x - 5y = -28 x - 4y = -30
A) (1, 9)
B) (-2, 9)
C) (2, 8)
D) no solution
x - 5y = -28 x - 4y = -30
A) (1, 9)
B) (-2, 9)
C) (2, 8)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
54
Find the solution to the system of equations by substitution.
-4x + y = 14 -5x + 8y = 4
A) (-2, -4)
B) (-3, -3)
C) (-4, -2)
D) no solution
-4x + y = 14 -5x + 8y = 4
A) (-2, -4)
B) (-3, -3)
C) (-4, -2)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
55
Find the solution to the system of equations by substitution.
x + y = 0 2x + 3y = -7
A) (-7, 7)
B) (6, -6)
C) (-6, 6)
D) (7, -7)
x + y = 0 2x + 3y = -7
A) (-7, 7)
B) (6, -6)
C) (-6, 6)
D) (7, -7)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
56
Find the solution by graphing the system of equations.
Sybil is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $180 for materials and equipment rental plus $60 per hour for labor. Company B gave and
Estimate of $220 for materials and equipment rental plus $50 per hour for labor. We can represent this situation with
The system of linear equations
C = 180 + 60h
C = 220 + 50h
Where c is the total cost and h is the number of hours of labor. Find the number of hours of labor for the two companies
To have the same total cost.
A) 3 hr
B) 7 hr
C) 4 hr
D) 8 hr
Sybil is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $180 for materials and equipment rental plus $60 per hour for labor. Company B gave and
Estimate of $220 for materials and equipment rental plus $50 per hour for labor. We can represent this situation with
The system of linear equations
C = 180 + 60h
C = 220 + 50h
Where c is the total cost and h is the number of hours of labor. Find the number of hours of labor for the two companies
To have the same total cost.
A) 3 hr
B) 7 hr
C) 4 hr
D) 8 hr

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
57
Find the solution to the system of equations by substitution.
x + 7y = -2 3x + y = 34
A) (3, 7)
B) (7, 12)
C) (12, -2)
D) (-2, 3)
x + 7y = -2 3x + y = 34
A) (3, 7)
B) (7, 12)
C) (12, -2)
D) (-2, 3)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
58
Find the solution to the system of equations by substitution.
y = 3x + 3 y = 8x + 2
A)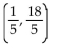
B)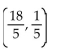
C) infinite number of solutions
D) no solution
y = 3x + 3 y = 8x + 2
A)
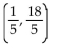
B)
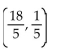
C) infinite number of solutions
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
59
Find the solution to the system of equations by substitution.
x - 5y = -4 x + 8y = -4
A) (4, 0)
B) (-4, 0)
C) (0, 4)
D) (0, -4)
x - 5y = -4 x + 8y = -4
A) (4, 0)
B) (-4, 0)
C) (0, 4)
D) (0, -4)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
60
Find the solution to the system of equations by substitution.
x y -= 2-y 3 = 11
A) (-3, 5)
B) (5, -3)
C) (17, -3)
D) (-5, -3)
x y -= 2-y 3 = 11
A) (-3, 5)
B) (5, -3)
C) (17, -3)
D) (-5, -3)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the system of equations using the addition method.
2x - 2y = 9 10x - 10y = 18
A)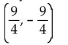
B) (9, 18)
C) infinite number of solutions
D) no solution
2x - 2y = 9 10x - 10y = 18
A)
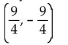
B) (9, 18)
C) infinite number of solutions
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the system of equations using the addition method.
2x + 40y = 40 4x - 5y = -5
A) (0, 0)
B) (1, 1)
C) (0, 1)
D) (1, 0)
2x + 40y = 40 4x - 5y = -5
A) (0, 0)
B) (1, 1)
C) (0, 1)
D) (1, 0)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
On a buying trip in Los Angeles, Rosaria Perez ordered 120 pieces of jewelry: a number of bracelets at $8 each and a number of necklaces at $10 each. She wrote a check for $1160 to pay for the order. How many bracelets
And how many necklaces did Rosaria purchase?
A) 30 bracelets and 90 necklaces
B) 25 bracelets and 95 necklaces
C) 20 bracelets and 100 necklaces
D) 15 bracelets and 105 necklaces
On a buying trip in Los Angeles, Rosaria Perez ordered 120 pieces of jewelry: a number of bracelets at $8 each and a number of necklaces at $10 each. She wrote a check for $1160 to pay for the order. How many bracelets
And how many necklaces did Rosaria purchase?
A) 30 bracelets and 90 necklaces
B) 25 bracelets and 95 necklaces
C) 20 bracelets and 100 necklaces
D) 15 bracelets and 105 necklaces

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
Devon purchased tickets to an air show for 4 adults and 2 children. The total cost was $144. The cost of a child's ticket was $3 less than the cost of an adult's ticket. Find the price of an adult's ticket and a child's ticket.
A) adult's ticket: $24; child's ticket: $21
B) adult's ticket: $27; child's ticket: $24
C) adult's ticket: $26; child's ticket: $23
D) adult's ticket: $25; child's ticket: $22
Devon purchased tickets to an air show for 4 adults and 2 children. The total cost was $144. The cost of a child's ticket was $3 less than the cost of an adult's ticket. Find the price of an adult's ticket and a child's ticket.
A) adult's ticket: $24; child's ticket: $21
B) adult's ticket: $27; child's ticket: $24
C) adult's ticket: $26; child's ticket: $23
D) adult's ticket: $25; child's ticket: $22

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
One number is four more than a second number. Two times the first number is 4 more than four times the second number.
A) - 6 and - 10
B) 6 and 2
C) 5 and 1
D) 7 and 3
One number is four more than a second number. Two times the first number is 4 more than four times the second number.
A) - 6 and - 10
B) 6 and 2
C) 5 and 1
D) 7 and 3

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
66
Find the solution to the system of equations by substitution.
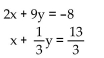
A) (5, 2)
B) (-5, -2)
C) (-5, 2)
D) (5, -2)
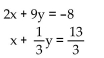
A) (5, 2)
B) (-5, -2)
C) (-5, 2)
D) (5, -2)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the system of equations using the addition method.
x - 5y = 3 x - 5y = 3
A)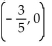
B)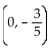
C) infinite number of solutions
D) no solution
x - 5y = 3 x - 5y = 3
A)
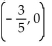
B)
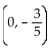
C) infinite number of solutions
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the system of equations using the addition method.
6x + 5y = -4 -6x - 11y = 16
A) (6, 2)
B) (-6, -2)
C) (-1, 2)
D) (1, -2)
6x + 5y = -4 -6x - 11y = 16
A) (6, 2)
B) (-6, -2)
C) (-1, 2)
D) (1, -2)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the system of equations using the addition method.
8x - 5y = 5 -16x + 10y = -20
A) (2, 4)
B)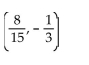
C) (8, 5)
D) no solution
8x - 5y = 5 -16x + 10y = -20
A) (2, 4)
B)
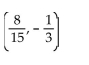
C) (8, 5)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 3 bags of potato chips for $12.50. Another customer buys 2 hot dogs and 3 bags of potato chips for $8.50. Find the cost of each item.
A) $2.00 for a hot dog; $1.75 for a bag of potato chips
B) $1.50 for a hot dog; $2.00 for a bag of potato chips
C) $2.25 for a hot dog; $1.75 for a bag of potato chips
D) $2.00 for a hot dog; $1.50 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 3 bags of potato chips for $12.50. Another customer buys 2 hot dogs and 3 bags of potato chips for $8.50. Find the cost of each item.
A) $2.00 for a hot dog; $1.75 for a bag of potato chips
B) $1.50 for a hot dog; $2.00 for a bag of potato chips
C) $2.25 for a hot dog; $1.75 for a bag of potato chips
D) $2.00 for a hot dog; $1.50 for a bag of potato chips

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the system of equations using the addition method.
6x + 4y = 48 6x + 2y = 60
A) (12, -6)
B) (-6, 12)
C) (-12, 4)
D) (-12, 6)
6x + 4y = 48 6x + 2y = 60
A) (12, -6)
B) (-6, 12)
C) (-12, 4)
D) (-12, 6)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the system of equations using the addition method.
x + 8y = -53 -6x + 7y = -12
A) (5, -5)
B) (-5, -6)
C) (-6, -5)
D) no solution
x + 8y = -53 -6x + 7y = -12
A) (5, -5)
B) (-5, -6)
C) (-6, -5)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
One number is 5 less than a second number. Twice the second number is 4 less than 4 times the first. Find the two numbers.
A) 7 and 12
B) 6 and 11
C) -12 and -7
D) 8 and 13
One number is 5 less than a second number. Twice the second number is 4 less than 4 times the first. Find the two numbers.
A) 7 and 12
B) 6 and 11
C) -12 and -7
D) 8 and 13

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
Two numbers total 8, and their difference is 16. Find the two numbers.
A) 4 and - 12
B) 8 and 2
C) 12 and - 4
D) 5 and 3
Two numbers total 8, and their difference is 16. Find the two numbers.
A) 4 and - 12
B) 8 and 2
C) 12 and - 4
D) 5 and 3

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the system of equations using the addition method.
2x + 24y = -110 8x + 6y = 10
A) (-6, 5)
B) (8, -8)
C) (-5, 5)
D) (5, -5)
2x + 24y = -110 8x + 6y = 10
A) (-6, 5)
B) (8, -8)
C) (-5, 5)
D) (5, -5)

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is $9.35 more
Than the value of the nickels. How many nickels and dimes does Jamil have?
A) 11 nickels and 99 dimes
B) 10 nickels and 90 dimes
C) 12 nickels and 108 dimes
D) 99 nickels and 11 dimes
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is $9.35 more
Than the value of the nickels. How many nickels and dimes does Jamil have?
A) 11 nickels and 99 dimes
B) 10 nickels and 90 dimes
C) 12 nickels and 108 dimes
D) 99 nickels and 11 dimes

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the system of equations using the addition method.
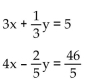
A) (-2, -4)
B) (2, -3)
C) (3, -4)
D) no solution
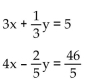
A) (-2, -4)
B) (2, -3)
C) (3, -4)
D) no solution

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 7 feet more than 3 times the width. He needs 46 feet of fencing to do the job. Find the length and
Width of the garden.
A) length: 22 ft; width: 5 ft
B) length: 16 ft; width: 3 ft
C)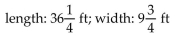
D) length: 19 ft; width: 4 ft
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 7 feet more than 3 times the width. He needs 46 feet of fencing to do the job. Find the length and
Width of the garden.
A) length: 22 ft; width: 5 ft
B) length: 16 ft; width: 3 ft
C)
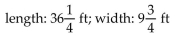
D) length: 19 ft; width: 4 ft

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem.
One number is 5 less than a second number. Twice the second number is 52 more than 5 times the first. Find the two numbers.
A) -13 and -8
B) -14 and -9
C) 9 and 14
D) -15 and -10
One number is 5 less than a second number. Twice the second number is 52 more than 5 times the first. Find the two numbers.
A) -13 and -8
B) -14 and -9
C) 9 and 14
D) -15 and -10

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem.
A bank teller has both $10 and $20 bills in her cash drawer. There are 31 $20 bills, and the total amount of all the bills is $740. How many $10 bills are there?
A) 12 $10 bills
B) 14 $10 bills
C) 31 $10 bills
D) 29 $10 bills
A bank teller has both $10 and $20 bills in her cash drawer. There are 31 $20 bills, and the total amount of all the bills is $740. How many $10 bills are there?
A) 12 $10 bills
B) 14 $10 bills
C) 31 $10 bills
D) 29 $10 bills

Unlock Deck
Unlock for access to all 139 flashcards in this deck.
Unlock Deck
k this deck


