Deck 11: Probability and Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 11: Probability and Calculus
1
Solve the problem.
Use the given function to find the indicated probabilities. Illustrate each probability with a graph.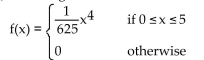
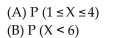
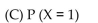
Use the given function to find the indicated probabilities. Illustrate each probability with a graph.
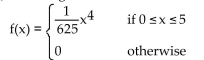
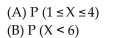
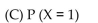
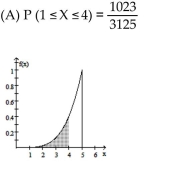
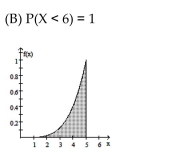
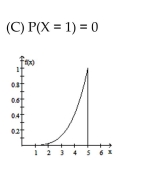
2
Find the associated cumulative distribution function. Graph both functions (on separate sets of axes).
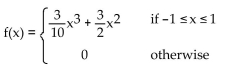
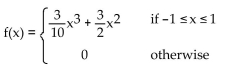
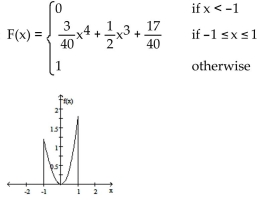
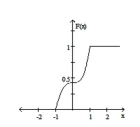
3
Find the associated cumulative distribution function. Graph both functions (on separate sets of axes).
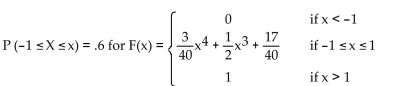
A) -0.27
B) 0.23
C) 0.68
D) -0.31
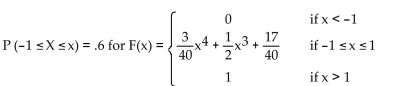
A) -0.27
B) 0.23
C) 0.68
D) -0.31
0.68
4
Find the value of the improper integral that converges.
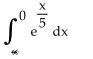
A) 5
B)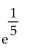
C) The improper integral diverges.
D)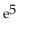
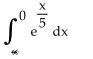
A) 5
B)
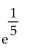
C) The improper integral diverges.
D)
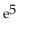

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
Find the value of the improper integral that converges.
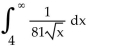
A) 9
B) 2
C) The improper integral diverges.
D)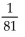
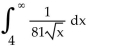
A) 9
B) 2
C) The improper integral diverges.
D)
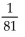

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the problem.
A trust fund produces a perpetual stream of income with rate flow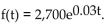 Find the capital value at 5% compounded continuously.
Find the capital value at 5% compounded continuously.
A) $135,000
B) $54,000
C) $90,000
D) $33,750
A trust fund produces a perpetual stream of income with rate flow
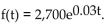 Find the capital value at 5% compounded continuously.
Find the capital value at 5% compounded continuously.A) $135,000
B) $54,000
C) $90,000
D) $33,750

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Graph y = f(x) and find the value of 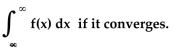
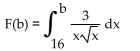
A)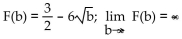
B)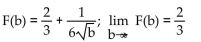
C)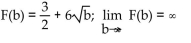
D)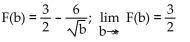
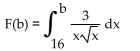
A)
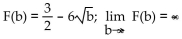
B)
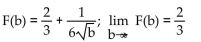
C)
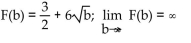
D)
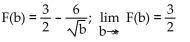

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the problem.
The perpetual annual rent for a property is $35,000. Find the capital value at 4% compounded continuously.
A) $98,500
B) $985,000
C) $875,000
D) $36,400
The perpetual annual rent for a property is $35,000. Find the capital value at 4% compounded continuously.
A) $98,500
B) $985,000
C) $875,000
D) $36,400

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Graph y = f(x) and find the value of 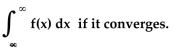

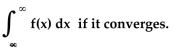


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the problem.
Find and graph the cumulative distribution function associated with the function.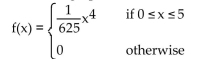
Find and graph the cumulative distribution function associated with the function.
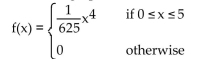

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the problem.
Find and graph the cumulative distribution function associated with the function.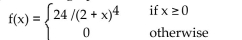
Find and graph the cumulative distribution function associated with the function.
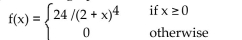

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the problem.
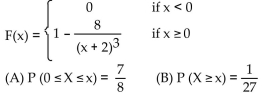
A) (A) 4; (B) 4
B) (A) 2; (B) 6
C) (A) 1; (B) 3
D) (A) 2; (B) 4
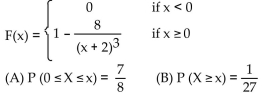
A) (A) 4; (B) 4
B) (A) 2; (B) 6
C) (A) 1; (B) 3
D) (A) 2; (B) 4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
Find the value of the improper integral that converges.
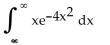
A) The improper integral diverges.
B) -4
C) 0
D)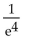
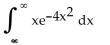
A) The improper integral diverges.
B) -4
C) 0
D)
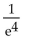

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the problem.
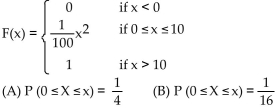
A) (A) 25; (B) 6.25
B) (A) 2.5; (B) 1.125
C) (A) 5; (B) 2.5
D) (A) 20; (B) 80
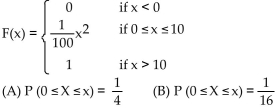
A) (A) 25; (B) 6.25
B) (A) 2.5; (B) 1.125
C) (A) 5; (B) 2.5
D) (A) 20; (B) 80

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
Find the associated cumulative distribution function. Graph both functions (on separate sets of axes).
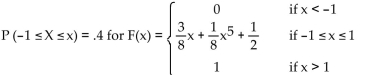
A) -0.27
B) 0.38
C) -0.62
D) 0.40
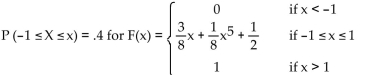
A) -0.27
B) 0.38
C) -0.62
D) 0.40

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
Graph y = f(x) and find the value of 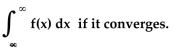
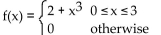
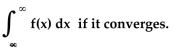
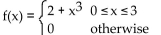

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the problem.
When a person takes a drug, the body does not assimilate all of the drug. One way to determine the amount of the drug assimilated is to measure the rate at which the drug is eliminated from the body. If the rate of
Elimination of the drug (in milliliters per minute) is given by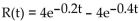 where t is the time in
where t is the time in
Minutes since the drug was administered, how much of the drug is eliminated from the body?
A) 10 mL
B) 2.5 mL
C) 25 mL
D) 100 mL
When a person takes a drug, the body does not assimilate all of the drug. One way to determine the amount of the drug assimilated is to measure the rate at which the drug is eliminated from the body. If the rate of
Elimination of the drug (in milliliters per minute) is given by
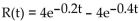 where t is the time in
where t is the time inMinutes since the drug was administered, how much of the drug is eliminated from the body?
A) 10 mL
B) 2.5 mL
C) 25 mL
D) 100 mL

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
Find F(b), use a graphing calculator to graph F 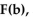 and use the graph to estimate
and use the graph to estimate 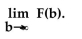
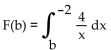
A)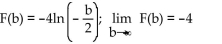
B)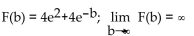
C)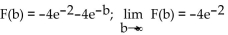
D)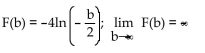
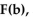 and use the graph to estimate
and use the graph to estimate 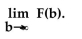
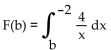
A)
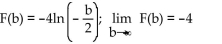
B)
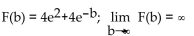
C)
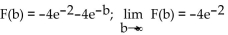
D)
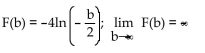

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Find the associated cumulative distribution function. Graph both functions (on separate sets of axes).
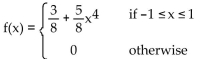
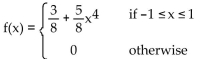

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.
Use the given function to find the indicated probabilities. Illustrate each probability with a graph.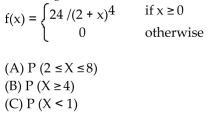
Use the given function to find the indicated probabilities. Illustrate each probability with a graph.
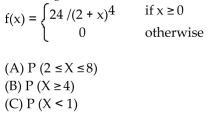

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Find a constant k so that kf is a probability density function, or state it does not exist.
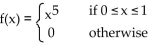
A)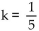
B)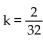
C) k = 6
D) does not exist
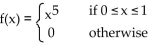
A)
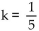
B)
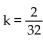
C) k = 6
D) does not exist

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.
Computer experts warn that writable compact disks such as CD-Rs (Compact Disc-Recordable) and CD-RWs
(Compact Disc-ReWriteable) have much shorter lifespans than other digital storage methods such as hard
drives or magnetic tape. The time until the disc becomes unreadable for a particular brand of CD-RWs is a
continuous random variable with probability density function given by the following function. Round to two decimal
places.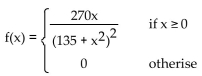 (A) What is the probability that a disc is not readable after 25 years?
(A) What is the probability that a disc is not readable after 25 years?
(B) What is the probability that the disc is readable after 10 years?
(C) If the user wants the probability that the disc is readable to be 0.9, when is the last time it should be read?
Computer experts warn that writable compact disks such as CD-Rs (Compact Disc-Recordable) and CD-RWs
(Compact Disc-ReWriteable) have much shorter lifespans than other digital storage methods such as hard
drives or magnetic tape. The time until the disc becomes unreadable for a particular brand of CD-RWs is a
continuous random variable with probability density function given by the following function. Round to two decimal
places.
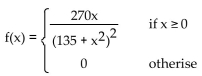 (A) What is the probability that a disc is not readable after 25 years?
(A) What is the probability that a disc is not readable after 25 years?(B) What is the probability that the disc is readable after 10 years?
(C) If the user wants the probability that the disc is readable to be 0.9, when is the last time it should be read?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Find the median for f(x).
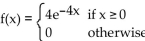 e
e
A)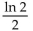
B)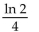
C)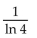
D)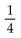
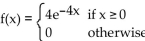 e
eA)
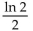
B)
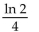
C)
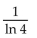
D)
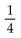

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.
The life expectancy (in minutes) of a certain microscopic organism is a continuous random variable with probability
density function given by the following function. Round to two decimal places.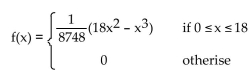 (A) What is the probability that an organism lives for at least 10 minutes?
(A) What is the probability that an organism lives for at least 10 minutes?
(B) What is the probability that an organism lives for at most 8 minutes?
The life expectancy (in minutes) of a certain microscopic organism is a continuous random variable with probability
density function given by the following function. Round to two decimal places.
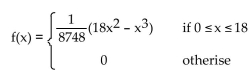 (A) What is the probability that an organism lives for at least 10 minutes?
(A) What is the probability that an organism lives for at least 10 minutes?(B) What is the probability that an organism lives for at most 8 minutes?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
The quartile points for a probability density function are the values 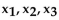 that divide the area under the graph of the
that divide the area under the graph of the
function into four equal parts. Find the quartile points for the probability density function f(x).
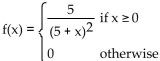
A)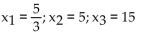
B)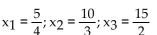
C)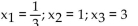
D)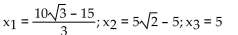
 that divide the area under the graph of the
that divide the area under the graph of thefunction into four equal parts. Find the quartile points for the probability density function f(x).
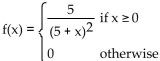
A)
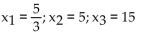
B)
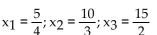
C)
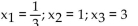
D)
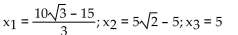

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem.
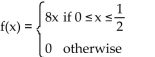
A)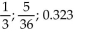
B)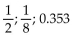
C)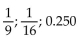
D)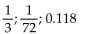
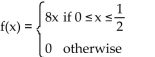
A)
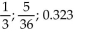
B)
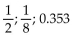
C)
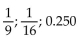
D)
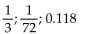

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
F(x) is the cumulative distribution function for a continuous random variable X. Find the probability density function f(x)
associated with F(x).
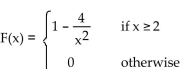
A)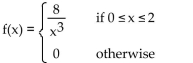
B)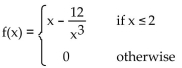
C)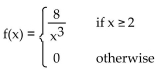
D)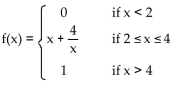
associated with F(x).
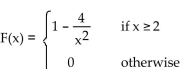
A)
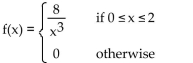
B)
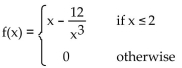
C)
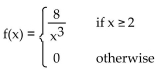
D)
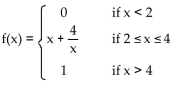

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
The quartile points for a probability density function are the values 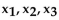 that divide the area under the graph of the
that divide the area under the graph of the
function into four equal parts. Find the quartile points for the probability density function f(x).
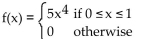
A)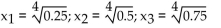
B)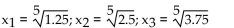
C)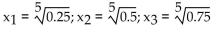
D)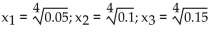
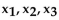 that divide the area under the graph of the
that divide the area under the graph of thefunction into four equal parts. Find the quartile points for the probability density function f(x).
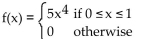
A)
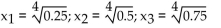
B)
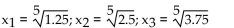
C)
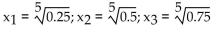
D)
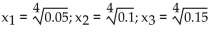

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
Find the median for f(x).
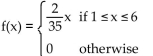
A)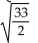
B)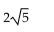
C)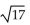
D)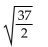
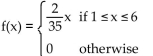
A)
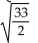
B)
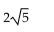
C)
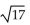
D)
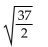

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
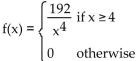
A) 48; 2,256; 47.497
B) 6; 48; 6.928
C) 96; 9,024; 94.995
D) 6; 12; 3.464
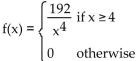
A) 48; 2,256; 47.497
B) 6; 48; 6.928
C) 96; 9,024; 94.995
D) 6; 12; 3.464

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
A building contractor's profit (in thousands of dollars) on each unit in a subdivision is a continuous random variable with probability density function f(x) as shown below.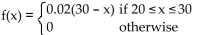 (A) Find the contractor's expected profit. Round to the nearest dollar.
(A) Find the contractor's expected profit. Round to the nearest dollar.
(B) Find the median profit. Round to the nearest dollar.
A) (A) $23,333; (B) $22,929
B) (A) $28,333; (B) $26,465
C) (A) $21,667; (B) $21,340
D) (A) $26,667; (B) $25,000
A building contractor's profit (in thousands of dollars) on each unit in a subdivision is a continuous random variable with probability density function f(x) as shown below.
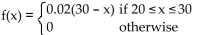 (A) Find the contractor's expected profit. Round to the nearest dollar.
(A) Find the contractor's expected profit. Round to the nearest dollar.(B) Find the median profit. Round to the nearest dollar.
A) (A) $23,333; (B) $22,929
B) (A) $28,333; (B) $26,465
C) (A) $21,667; (B) $21,340
D) (A) $26,667; (B) $25,000

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
Find the probability density function f and the associated cumulative distribution function F for the continuous random
variable X if
X is uniformly distributed on [1, 7].
A)![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40db_b437_110987f5371e_TB8593_11.jpg)
B)![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40dc_b437_551e411e525d_TB8593_11.jpg) 7
7
C)![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40dd_b437_277a64687a9a_TB8593_11.jpg)
D)![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40de_b437_77a52082b7c2_TB8593_11.jpg)
variable X if
X is uniformly distributed on [1, 7].
A)
![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40db_b437_110987f5371e_TB8593_11.jpg)
B)
![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40dc_b437_551e411e525d_TB8593_11.jpg) 7
7C)
![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40dd_b437_277a64687a9a_TB8593_11.jpg)
D)
![<strong>Find the probability density function f and the associated cumulative distribution function F for the continuous random variable X if X is uniformly distributed on [1, 7].</strong> A) B) 7 C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_40de_b437_77a52082b7c2_TB8593_11.jpg)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the problem.
The time (in minutes) a customer must wait in line at a bank is a continuous random variable with probability density function f(x) as shown below.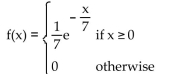 Find the median waiting time. Round to three decimal places.
Find the median waiting time. Round to three decimal places.
A) 0.693 minutes
B) 0.143 minutes
C) 3.892 minutes
D) 4.852 minutes
The time (in minutes) a customer must wait in line at a bank is a continuous random variable with probability density function f(x) as shown below.
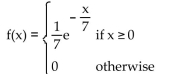 Find the median waiting time. Round to three decimal places.
Find the median waiting time. Round to three decimal places.A) 0.693 minutes
B) 0.143 minutes
C) 3.892 minutes
D) 4.852 minutes

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
Find a constant k so that kf is a probability density function, or state it does not exist.
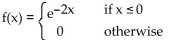
A)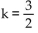
B) k = -2
C) does not exist
D) k = 2
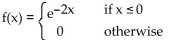
A)
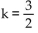
B) k = -2
C) does not exist
D) k = 2

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Use a graphing calculator to approximate the median of the indicated probability density function f. Round to two
decimal places.
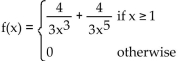
A) 1.78
B) 1.27
C) 1.56
D) 1.31
decimal places.
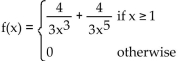
A) 1.78
B) 1.27
C) 1.56
D) 1.31

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
F(x) is the cumulative distribution function for a continuous random variable X. Find the probability density function f(x)
associated with F(x).
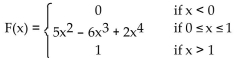
A)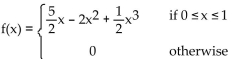
B)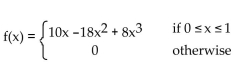
C)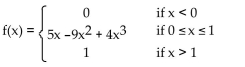
D)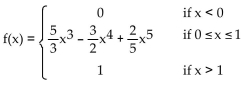
associated with F(x).
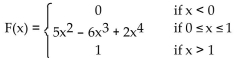
A)
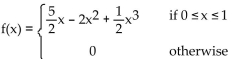
B)
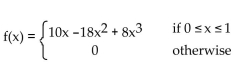
C)
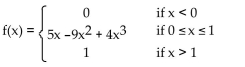
D)
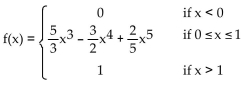

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Use a graphing calculator to approximate the median of the indicated probability density function f. Round to two
decimal places.
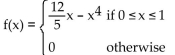
A) 0.46
B) 0.36
C) 0.63
D) 0.66
decimal places.
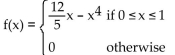
A) 0.46
B) 0.36
C) 0.63
D) 0.66

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
Popular online video games often struggle to meet the initially high demand for access to the game servers. It is
costly to increase server capacity and the demand always falls after a few months, but if the wait times are too
long the game could lose sales as a result of negative criticism. The time (in minutes) a customer must wait to
get into the game is a continuous random variable with probability density function given by the following
function. Round to two decimal places.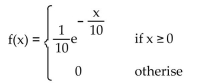 (A) Evaluate
(A) Evaluate 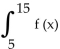 dx and interpret the results.
dx and interpret the results.
(B) What is the probability that a customer waits less than 7 minutes?
(C) What is the probability that a customer waits more than 10 minutes?
Popular online video games often struggle to meet the initially high demand for access to the game servers. It is
costly to increase server capacity and the demand always falls after a few months, but if the wait times are too
long the game could lose sales as a result of negative criticism. The time (in minutes) a customer must wait to
get into the game is a continuous random variable with probability density function given by the following
function. Round to two decimal places.
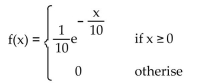 (A) Evaluate
(A) Evaluate 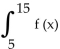 dx and interpret the results.
dx and interpret the results.(B) What is the probability that a customer waits less than 7 minutes?
(C) What is the probability that a customer waits more than 10 minutes?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
The shelf life (in days) of a perishable drug is a continuous random variable with probability density function f(x) as shown below.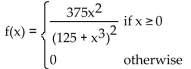 Find the median shelf life.
Find the median shelf life.
A) 125 days
B) 5 days
C) 15 days
D) 25 days
The shelf life (in days) of a perishable drug is a continuous random variable with probability density function f(x) as shown below.
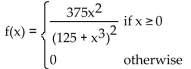 Find the median shelf life.
Find the median shelf life.A) 125 days
B) 5 days
C) 15 days
D) 25 days

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Find the probability density function f and the associated cumulative distribution function F for the continuous random
variable X if
X is an exponential random variable with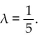
A)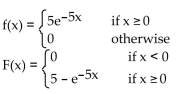
B)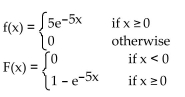
C)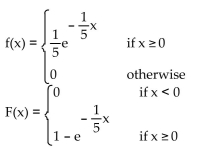
D)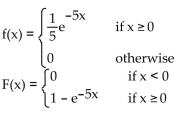
variable X if
X is an exponential random variable with
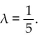
A)
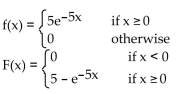
B)
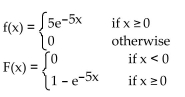
C)
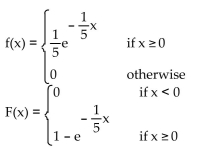
D)
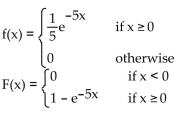

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
Find the area under the standard normal curve from 0 to the indicated value of z. 0.85
A) 0.3023
B) 0.8023
C) 0.6977
D) 0.1977
Find the area under the standard normal curve from 0 to the indicated value of z. 0.85
A) 0.3023
B) 0.8023
C) 0.6977
D) 0.1977

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
X is a continuous random variable with mean 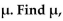 and then find
and then find 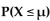 ) if
) if
X is an exponential random variable with λ = 4.
A)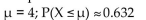
B)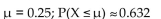
C)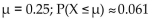
D)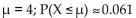
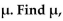 and then find
and then find 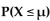 ) if
) ifX is an exponential random variable with λ = 4.
A)
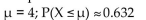
B)
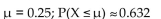
C)
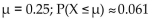
D)
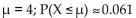

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
Find the mean, median, and standard deviation of the continuous random variable X if
X is uniformly distributed on [4, 8].
A)![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f4_b437_4d17a3dbd83b_TB8593_11.jpg)
B)![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f5_b437_a97fa94866a8_TB8593_11.jpg)
C)![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f6_b437_b91323789d2e_TB8593_11.jpg)
D)![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_8f07_b437_0db4544c5cbe_TB8593_11.jpg)
X is uniformly distributed on [4, 8].
A)
![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f4_b437_4d17a3dbd83b_TB8593_11.jpg)
B)
![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f5_b437_a97fa94866a8_TB8593_11.jpg)
C)
![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_67f6_b437_b91323789d2e_TB8593_11.jpg)
D)
![<strong>Find the mean, median, and standard deviation of the continuous random variable X if X is uniformly distributed on [4, 8].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_8f07_b437_0db4544c5cbe_TB8593_11.jpg)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
Given a normal distribution with mean 40 and standard deviation 8, find the number of standard deviations the
measurement is from the mean. Express the answer as a positive number.
24
A) 8
B) 16
C) 0.5
D) 2
measurement is from the mean. Express the answer as a positive number.
24
A) 8
B) 16
C) 0.5
D) 2

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
The time (in minutes) applicants must wait to receive a driver's examination is uniformly distributed on the interval [0, 80]. What is the probability that an applicant must wait more than 30 minutes?
A) 0.8125
B) 0.375
C) 0.1875
D) 0.625
The time (in minutes) applicants must wait to receive a driver's examination is uniformly distributed on the interval [0, 80]. What is the probability that an applicant must wait more than 30 minutes?
A) 0.8125
B) 0.375
C) 0.1875
D) 0.625

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Given a normal distribution with mean 150 and standard deviation 25, find the indicated probability.
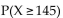
A) 0.8415
B) 0.1585
C) 0.5793
D) 0.4207
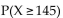
A) 0.8415
B) 0.1585
C) 0.5793
D) 0.4207

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
The life expectancy of a car battery is normally distributed. The average (mean) lifetime is 235 weeks with a standard deviation of 15 weeks. If the company guarantees the battery for 4 years, what percentage of the
Batteries sold would be expected to be returned before the end of the warranty period?
A) 0.0719
B) 0.9281
C) 0.0359
D) 0.9641
The life expectancy of a car battery is normally distributed. The average (mean) lifetime is 235 weeks with a standard deviation of 15 weeks. If the company guarantees the battery for 4 years, what percentage of the
Batteries sold would be expected to be returned before the end of the warranty period?
A) 0.0719
B) 0.9281
C) 0.0359
D) 0.9641

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
Find the area under the standard normal curve and above the given interval on the horizontal axis.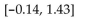
A) 0.0557
B) 0.4236
C) 0.4793
D) 0.5207
Find the area under the standard normal curve and above the given interval on the horizontal axis.
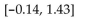
A) 0.0557
B) 0.4236
C) 0.4793
D) 0.5207

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
Given a normal distribution with mean 40 and standard deviation 8, find the number of standard deviations the
measurement is from the mean. Express the answer as a positive number.
50
A) 1.25
B) 0.8
C) 10
D) 2
measurement is from the mean. Express the answer as a positive number.
50
A) 1.25
B) 0.8
C) 10
D) 2

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
Find the mean, median, and standard deviation of the continuous random variable X if
X is an exponential random variable with λ = 2.
A)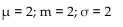
B)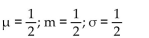
C)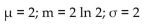
D)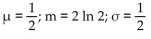
X is an exponential random variable with λ = 2.
A)
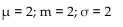
B)
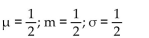
C)
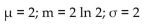
D)
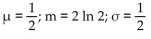

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
The length of time for telephone conversations (in minutes) is exponentially distributed. The average (mean) length of a conversation is 5 minutes. What is the probability that a conversation lasts less than 3 minutes?
A) 0.189
B) 0.451
C) 0.549
D) 0.811
The length of time for telephone conversations (in minutes) is exponentially distributed. The average (mean) length of a conversation is 5 minutes. What is the probability that a conversation lasts less than 3 minutes?
A) 0.189
B) 0.451
C) 0.549
D) 0.811

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Given a normal distribution with mean -10 and standard deviation 5, find the area under the normal curve and above the
given interval on the horizontal axis.
(-∞ , -5]
A) 0.6827
B) 0.1587
C) 0.3173
D) 0.8413
given interval on the horizontal axis.
(-∞ , -5]
A) 0.6827
B) 0.1587
C) 0.3173
D) 0.8413

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ)
if
X is uniformly distributed on [-6, 6].
A)![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_0448_b437_4760d053c4f1_TB8593_11.jpg)
B)![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_0449_b437_e59948d9794d_TB8593_11.jpg)
C)![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_044a_b437_f14506652159_TB8593_11.jpg)
D)![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_044b_b437_1bf0a4421af8_TB8593_11.jpg)
if
X is uniformly distributed on [-6, 6].
A)
![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_0448_b437_4760d053c4f1_TB8593_11.jpg)
B)
![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_0449_b437_e59948d9794d_TB8593_11.jpg)
C)
![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_044a_b437_f14506652159_TB8593_11.jpg)
D)
![<strong>X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ) if X is uniformly distributed on [-6, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d4_044b_b437_1bf0a4421af8_TB8593_11.jpg)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
Given a normal distribution with mean -10 and standard deviation 5, find the area under the normal curve and above the
given interval on the horizontal axis.
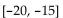
A) 0.0228
B) 0.1815
C) 0.1587
D) 0.1359
given interval on the horizontal axis.
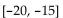
A) 0.0228
B) 0.1815
C) 0.1587
D) 0.1359

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
X is a continuous random variable with mean µ and standard deviation σ. Find µ and σ, and then find P(µ -σ ≤ X ≤ µ +σ)
if
X is an exponential random variable with m = 2 ln 2.
A)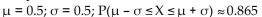
B)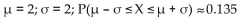
C)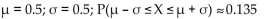
D)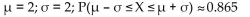
if
X is an exponential random variable with m = 2 ln 2.
A)
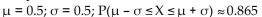
B)
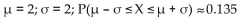
C)
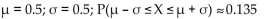
D)
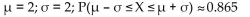

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
X is a continuous random variable with mean ![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_b61e_b437_23b021cd7373_TB8593_11.jpg) and then find
and then find ![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_b61f_b437_b55f2509165f_TB8593_11.jpg) ) if
) if
X is uniformly distributed on [0, 6].
A)![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd30_b437_357a389579a4_TB8593_11.jpg)
B)![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd31_b437_eda5a355f5a8_TB8593_11.jpg)
C)![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd32_b437_259196656868_TB8593_11.jpg)
D)![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd33_b437_41deb5f17c3f_TB8593_11.jpg)
![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_b61e_b437_23b021cd7373_TB8593_11.jpg) and then find
and then find ![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_b61f_b437_b55f2509165f_TB8593_11.jpg) ) if
) ifX is uniformly distributed on [0, 6].
A)
![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd30_b437_357a389579a4_TB8593_11.jpg)
B)
![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd31_b437_eda5a355f5a8_TB8593_11.jpg)
C)
![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd32_b437_259196656868_TB8593_11.jpg)
D)
![<strong>X is a continuous random variable with mean and then find ) if X is uniformly distributed on [0, 6].</strong> A) B) C) D)](https://storage.examlex.com/TB8593/11ebb6d7_48d3_dd33_b437_41deb5f17c3f_TB8593_11.jpg)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
Given a normal distribution with mean 150 and standard deviation 25, find the indicated probability.
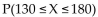
A) 0.8849
B) 0.2118
C) 0.3269
D) 0.6731
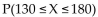
A) 0.8849
B) 0.2118
C) 0.3269
D) 0.6731

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck


