Deck 7: Continuous Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/167
Play
Full screen (f)
Deck 7: Continuous Probability Distributions
1
If X is a continuous random variable on the interval [0, 10], then P ( X = 5)= f (5)= 1\10.
False
2
Let X represent weekly income expressed in dollars. Since there is no set upper limit, we cannot identify (and thus cannot count)all the possible values. Consequently, weekly income is regarded as a continuous random variable.
True
3
A continuous random variable X has a uniform distribution between 5 and 25 (inclusive), then P ( X = 15)= 0.05.
False
4
If we standardize the normal curve, we express the original X values in terms of their number of standard deviations away from the mean.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
5
A continuous random variable X has a uniform distribution between 10 and 20 (inclusive), then the probability that X falls between 12 and 15 is 0.30.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
6
We distinguish between discrete and continuous random variables by noting whether the number of possible values is countable or uncountable.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
7
The sum of all values of f(x)over the range of [ a , b ] must equal one.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
8
Continuous probability distributions describe probabilities associated with random variables that are able to assume any finite number of values along an interval.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
9
A national standardized testing company can tell you your relative standing on an exam without divulging the mean or the standard deviation of the exam scores.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
10
If X is a continuous random variable on the interval [0, 10], then P ( X > 5)= P ( X ³ 5).

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
11
To be a legitimate probability density function, all possible values of f(x)must lie between 0 and 1 (inclusive).

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
12
If your golf score is 3 standard deviations below the mean, its corresponding value on the Z distribution is - 3.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
13
Since there is an infinite number of values a continuous random variable can assume, the probability of each individual value is virtually 0.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
14
A probability density function shows the probability for each value of X .

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
15
If a point y lies outside the range of the possible values of a random variable X , then f(y)must equal zero.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
16
A continuous probability distribution represents a random variable having an infinite number of outcomes which may assume any number of values within an interval.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
17
In practice, we frequently use a continuous distribution to approximate a discrete one when the number of values the variable can assume is countable but very large.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
18
A continuous random variable X has a uniform distribution between 5 and 15 (inclusive), then the probability that X falls between 10 and 20 is 1.0.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
19
To be a legitimate probability density function, all possible values of f(x)must be non-negative.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
20
A continuous random variable is one that can assume an uncountable number of values.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
21
The value of A such that P ( - A £ t £ A )= 0.95, where the degrees of freedom are 20, is 2.086.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
22
The value of an F distribution with v 1 = 5 and v 2 = 10 degrees of freedom such that the area to its left is 0.95 is 3.33.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
23
Like that of the Student t distribution, the shape of the chi-squared distribution depends on its number of degrees of freedom.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
24
A normal distribution is symmetric; therefore the probability of being below the mean is 0.50 and the probability of being above the mean is 0.50.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
25
We define 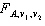 as the value of the F with v 1 and v 2 degrees of freedom such that the area to its right under the F curve is A , while
as the value of the F with v 1 and v 2 degrees of freedom such that the area to its right under the F curve is A , while 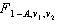 is defined as the value such that the area to its left is A .
is defined as the value such that the area to its left is A .
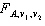 as the value of the F with v 1 and v 2 degrees of freedom such that the area to its right under the F curve is A , while
as the value of the F with v 1 and v 2 degrees of freedom such that the area to its right under the F curve is A , while 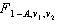 is defined as the value such that the area to its left is A .
is defined as the value such that the area to its left is A .
Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
26
The variance of a c 2 distribution is twice the value of its mean.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
27
As the degrees of freedom approach infinity, the values of a Student t distribution approach those of a standard normal distribution.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
28
A random variable X has a normal distribution with mean 132 and variance 36. If x = 120, its corresponding value of Z is 2.0.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
29
The variance of a Student t random variable with v degrees of freedom ( v > 2)is always greater than 1.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
30
The probability that Z is less than - 2 is the same as one minus the probability that Z is greater than +2.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
31
The value of c 2 with v degrees of freedom such that the area to its right under the chi-squared curve is equal to A is denoted by 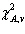 , while
, while 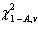 denotes the value such that the area to its left is A .
denotes the value such that the area to its left is A .
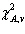 , while
, while 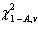 denotes the value such that the area to its left is A .
denotes the value such that the area to its left is A .
Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
32
The expected value of the Student t distribution is zero.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
33
A random variable X has a normal distribution with a mean of 250 and a standard deviation of 50. Given that X = 175, its corresponding value of Z is - 1.50.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
34
If the value of Z is z = 99, that means you are at the 99th percentile on the Z distribution.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
35
In the standard normal distribution, z 0.05 = 1.645 means that 5% of all values of z are below 1.645 and 95% are above it.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose X has a normal distribution with mean 70 and standard deviation 5. The 50th percentile of X is 70.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
37
The 10th percentile of a Z distribution has 10% of the Z -values lying above it.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
38
The probability that a standard normal random variable Z is less than - 3.5 is approximately 0.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
39
Given that Z is a standard normal random variable, a negative value of Z indicates that the standard deviation of Z is negative.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
40
A random variable X is standardized by subtracting the mean and dividing by the variance.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
41
What is the shape of the probability density function for a uniform random variable on the interval [ a , b ]?
A)A rectangle whose X values go from a to b .
B)A straight line whose height is 1 \( b - a )over the range [ a , b ].
C)A continuous probability density function with the same value of f(x)from a to b .
D)All of these choices are true.
A)A rectangle whose X values go from a to b .
B)A straight line whose height is 1 \( b - a )over the range [ a , b ].
C)A continuous probability density function with the same value of f(x)from a to b .
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following is not a characteristic for a normal distribution?
A)It is symmetrical.
B)The mean is always zero.
C)The mean, median, and mode are all equal.
D)It is a bell-shaped distribution.
A)It is symmetrical.
B)The mean is always zero.
C)The mean, median, and mode are all equal.
D)It is a bell-shaped distribution.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
43
The variance of a Student t distribution approaches zero as the degrees of freedom approaches infinity.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
44
The probability density function, f(x), for any continuous random variable X , represents:
A)all possible values that X will assume within some interval a £ x £ b .
B)the probability that X takes on a specific value x.
C)the height of the density function at x .
D)None of these choices.
A)all possible values that X will assume within some interval a £ x £ b .
B)the probability that X takes on a specific value x.
C)the height of the density function at x .
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
45
If X has a normal distribution with mean 60 and standard deviation 6, which value of X corresponds with the value z = 1.96?
A)x = 71.76
B)x = 67.96
C)x = 61.96
D)x = 48.24
A)x = 71.76
B)x = 67.96
C)x = 61.96
D)x = 48.24

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
46
The Student t distribution looks similar in shape to a standard normal distribution, except it is not as widely spread.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
47
The value of a chi-squared distribution with 8 degrees of freedom such that the area to its left is 0.95 is 2.73.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
48
Which of the following does not represent a continuous uniform random variable?
A)f(x)= 1\2 for x between - 1 and 1, inclusive.
B)f(x)= 10 for x between 0 and 1\10, inclusive.
C)f(x)= 1\3 for x = 4, 5, 6.
D)None of these choices represents a continuous uniform random variable.
A)f(x)= 1\2 for x between - 1 and 1, inclusive.
B)f(x)= 10 for x between 0 and 1\10, inclusive.
C)f(x)= 1\3 for x = 4, 5, 6.
D)None of these choices represents a continuous uniform random variable.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose f(x)= 1\4 over the range a £ x £ b , and suppose P ( X > 4)= 1\2. What are the values for a and b ?
A)0 and 4
B)2 and 6
C)Can be any range of x values whose length ( b - a )equals 4.
D)Cannot answer with the information given.
A)0 and 4
B)2 and 6
C)Can be any range of x values whose length ( b - a )equals 4.
D)Cannot answer with the information given.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
50
The value of a chi-squared distribution with 5 degrees of freedom such that the area to its left is 0.10 is 1.61.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
51
The probability density function f(x)of a random variable X that has a uniform distribution between a and b is
A)( b + a )\2
B)1\ b - 1\ a
C)( a - b )\2
D)None of these choices.
A)( b + a )\2
B)1\ b - 1\ a
C)( a - b )\2
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
52
What proportion of the data from a normal distribution is within two standard deviations from the mean?
A)0.3413
B)0.4772
C)0.6826
D)0.9544
A)0.3413
B)0.4772
C)0.6826
D)0.9544

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
53
Which of the following is always true for all probability density functions of continuous random variables?
A)The probability at any single point is zero.
B)They contain an uncountable number of possible values.
C)The total area under the density function f(x)equals 1.
D)All of these choices are true.
A)The probability at any single point is zero.
B)They contain an uncountable number of possible values.
C)The total area under the density function f(x)equals 1.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following is true about f(x)when X has a uniform distribution over the interval [ a , b ]?
A)The values of f(x)are different for various values of the random variable X.
B)f(x)equals one for each possible value of X .
C)f(x)equals one divided by the length of the interval from a to b .
D)None of these choices.
A)The values of f(x)are different for various values of the random variable X.
B)f(x)equals one for each possible value of X .
C)f(x)equals one divided by the length of the interval from a to b .
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following represents a difference between continuous and discrete random variables?
A)Continuous random variables assume an uncountable number of values, and discrete random variables do not.
B)The probability for any individual value of a continuous random variable is zero, but for discrete random variables it is not.
C)Probability for continuous random variables means finding the area under a curve, while for discrete random variables it means summing individual probabilities.
D)All of these choices are true.
A)Continuous random variables assume an uncountable number of values, and discrete random variables do not.
B)The probability for any individual value of a continuous random variable is zero, but for discrete random variables it is not.
C)Probability for continuous random variables means finding the area under a curve, while for discrete random variables it means summing individual probabilities.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
56
The probability density function f(x)for a uniform random variable X defined over the interval [2, 10] is
A)0.20
B)8
C)4
D)None of these choices.
A)0.20
B)8
C)4
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose f(x)= 0.25. What range of possible values can X take on and still have the density function be legitimate?
A)[0, 4]
B)[4, 8]
C)[ - 2, +2]
D)All of these choices are true.
A)[0, 4]
B)[4, 8]
C)[ - 2, +2]
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
58
If the random variable X has a uniform distribution between 40 and 50, then P (35 £ X £ 45)is:
A)1.0
B)0.5
C)0.1
D)undefined.
A)1.0
B)0.5
C)0.1
D)undefined.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
59
The value of an F distribution with v 1 = 6 and v 2 = 9 degrees of freedom such that the area to its right is 0.05 is 3.37.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
60
A standard normal distribution is a normal distribution with:
A)a mean of zero and a standard deviation of one.
B)a mean of one and a standard deviation of zero.
C)a mean always larger than the standard deviation.
D)None of these choices.
A)a mean of zero and a standard deviation of one.
B)a mean of one and a standard deviation of zero.
C)a mean always larger than the standard deviation.
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose Lamont's exam score was at the 80th percentile on an exam whose mean was 90. What was Lamont's exam score?
A)76.81
B)72.00
C)80.00
D)Cannot tell without more information.
A)76.81
B)72.00
C)80.00
D)Cannot tell without more information.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
62
Tanner took a statistics test whose mean was 80 and standard deviation was 5. The total points possible was 100. Tanner's score was 2 standard deviations below the mean. What was Tanner's score, rounded to the nearest whole number?
A)78
B)70
C)90
D)None of these choices.
A)78
B)70
C)90
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
63
Given that Z is a standard normal random variable, the area to the left of a value z is expressed as
A)P ( Z ³ z )
B)P ( Z £ z )
C)P (0 £ Z £ z )
D)P ( Z ³ - z )
A)P ( Z ³ z )
B)P ( Z £ z )
C)P (0 £ Z £ z )
D)P ( Z ³ - z )

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
64
What number corresponds to t 0.05,10?
A)1.812
B)1.372
C)2.228
D)1.833
A)1.812
B)1.372
C)2.228
D)1.833

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
65
Given that Z is a standard normal random variable, a negative value ( z )on its distribution would indicate:
A)z is to the left of the mean.
B)the standard deviation of this Z distribution is negative.
C)the area between zero and the value z is negative.
D)None of these choices.
A)z is to the left of the mean.
B)the standard deviation of this Z distribution is negative.
C)the area between zero and the value z is negative.
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
66
Given that Z is a standard normal variable, the variance of Z :
A)is always greater than 2.0.
B)is always greater than 1.0.
C)is always equal to 1.0.
D)cannot assume a specific value.
A)is always greater than 2.0.
B)is always greater than 1.0.
C)is always equal to 1.0.
D)cannot assume a specific value.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
67
Which of the following statements is false?
A)The chi-squared distribution is positively skewed.
B)All the values of the chi-squared distribution are non-negative.
C)The shape of the chi-squared distribution depends on its degrees of freedom.
D)All of these choices are true.
A)The chi-squared distribution is positively skewed.
B)All the values of the chi-squared distribution are non-negative.
C)The shape of the chi-squared distribution depends on its degrees of freedom.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
68
If 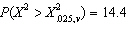 , then the number of degrees of freedom v is:
, then the number of degrees of freedom v is:
A)5
B)6
C)7
D)8
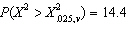 , then the number of degrees of freedom v is:
, then the number of degrees of freedom v is:A)5
B)6
C)7
D)8

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
69
Lamont took a psychology exam whose mean was 70 with standard deviation 5. He also took a calculus exam whose mean was 80 with standard deviation 10. He scored 85 on both exams. On which exam did he do better compared to the other students who took the exam?
A)He did better on the psychology exam, comparatively speaking.
B)He did better on the calculus exam, comparatively speaking.
C)He did the same on both exams, relatively speaking.
D)Cannot tell without more information.
A)He did better on the psychology exam, comparatively speaking.
B)He did better on the calculus exam, comparatively speaking.
C)He did the same on both exams, relatively speaking.
D)Cannot tell without more information.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
70
What number corresponds to 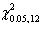 ?
?
A)28.30
B)26.22
C)21.00
D)5.23
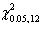 ?
?A)28.30
B)26.22
C)21.00
D)5.23

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
71
Most values of a standard normal distribution lie between:
A)0 and 1
B)- 3 and 3
C)0 and 3
D)minus infinity and plus infinity
A)0 and 1
B)- 3 and 3
C)0 and 3
D)minus infinity and plus infinity

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
72
The Student t distribution:
A)is symmetrical.
B)approaches the normal distribution as the degrees of freedom increase.
C)has more area in the tails than the standard normal distribution does.
D)All of these choices are true.
A)is symmetrical.
B)approaches the normal distribution as the degrees of freedom increase.
C)has more area in the tails than the standard normal distribution does.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
73
The Student t distribution with parameter v = 2 has a mean E ( t )equal to:
A)0
B)1
C)2
D)None of these choices.
A)0
B)1
C)2
D)None of these choices.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
74
Which of the following statements is correct regarding the percentile points of the F distribution?
A)F 0.10,10,20 = 1\ F 0.90,10,20
B)F 0.90,10,20 = 1\ F 0.10,20,10
C)F 0.90,10,20 = 1\ F 0.90,20,10
D)F 0.10,10,20 = 1\ F 0.10,20,10
A)F 0.10,10,20 = 1\ F 0.90,10,20
B)F 0.90,10,20 = 1\ F 0.10,20,10
C)F 0.90,10,20 = 1\ F 0.90,20,10
D)F 0.10,10,20 = 1\ F 0.10,20,10

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
75
The Student t distribution with parameter v = 4 has a variance V ( t )equal to:
A)4
B)0
C)2
D)1
A)4
B)0
C)2
D)1

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
76
If P ( t > t .01, v )= 2.50, then the number of degrees of freedom v is:
A)20
B)21
C)22
D)23
A)20
B)21
C)22
D)23

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
77
In its standardized form, the normal distribution:
A)has a mean of 0 and a standard deviation of 1.
B)has a mean of 1 and a variance of 0.
C)has an area equal to 0.5.
D)cannot be used to approximate discrete probability distributions.
A)has a mean of 0 and a standard deviation of 1.
B)has a mean of 1 and a variance of 0.
C)has an area equal to 0.5.
D)cannot be used to approximate discrete probability distributions.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
78
What number corresponds to F 0.95,4,8?
A)6.040
B)3.840
C)0.260
D)0.166
A)6.040
B)3.840
C)0.260
D)0.166

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
79
Stacy took a math test whose mean was 70 and standard deviation was 5. The total points possible was 100. Stacey's results were reported to be at the 95th percentile. What was Stacey's actual exam score, rounded to the nearest whole number?
A)95
B)78
C)75
D)62
A)95
B)78
C)75
D)62

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck
80
A larger standard deviation of a normal distribution indicates that the distribution becomes:
A)narrower and more peaked.
B)flatter and wider.
C)more skewed to the right.
D)more skewed to the left.
A)narrower and more peaked.
B)flatter and wider.
C)more skewed to the right.
D)more skewed to the left.

Unlock Deck
Unlock for access to all 167 flashcards in this deck.
Unlock Deck
k this deck


