Deck 14: Developing Aspects of Proportional Reasoning: Ratio, Proportion, and Percent
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 14: Developing Aspects of Proportional Reasoning: Ratio, Proportion, and Percent
1
Changing 17 to a percent is equivalent to the value:
A)0.17%.
B)0.0017%.
C)170%.
D)1700%.
A)0.17%.
B)0.0017%.
C)170%.
D)1700%.
1700%.
2
A bag of marbles contained 6 green marbles and 8 red marbles. A child who noticed a 6:14 ratio would be using the following meaning of ratios:
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)probability relationships
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)probability relationships
part-whole sense
3
For the problem:
Five shirts require 10 yards of cloth. How many yards of cloth will 15 shirts require?
This problem can be set up in all the following ways except for:
A)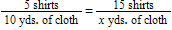
B)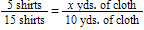
C)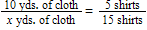
D)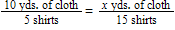
Five shirts require 10 yards of cloth. How many yards of cloth will 15 shirts require?
This problem can be set up in all the following ways except for:
A)
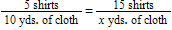
B)
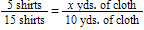
C)
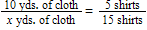
D)
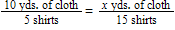
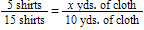
4
The price of a $5.00 hat is increased 20% to $6.00, then later, the hat is reduced back down to $5.00. Which of the following is a true statement?
A)The percent of decrease is the same as the percent of increase.
B)The percent of decrease is less than the percent of increase.
C)The percent of decrease is more than the percent of increase.
D)The percent of increase followed by a percent of decrease cannot always be determined.
A)The percent of decrease is the same as the percent of increase.
B)The percent of decrease is less than the percent of increase.
C)The percent of decrease is more than the percent of increase.
D)The percent of increase followed by a percent of decrease cannot always be determined.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
The following are true statements about proportions except for :
A)proportions are common fraction relationships.
B)any problem solved using a rate table can be solved using a proportion.
C)proportions can be explained in terms of equivalent fractions.
D)proportions are equalities between two ratios.
A)proportions are common fraction relationships.
B)any problem solved using a rate table can be solved using a proportion.
C)proportions can be explained in terms of equivalent fractions.
D)proportions are equalities between two ratios.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
All of the following are true statements about common fractions and ratios except for :
A)common fractions do not require labels for each of their parts like ratios do.
B)neither common fractions nor ratios can have zeros in the denominator (common fraction)or second position (ratio).
C)ratios can have parts added to them such as when the ratio of boys to girls in a class changes when new students add the class; common fractions cannot.
D)ratios are not independent numerical expressions and must be understood in the context of the relationships they represent; common fractions are independent of context.
A)common fractions do not require labels for each of their parts like ratios do.
B)neither common fractions nor ratios can have zeros in the denominator (common fraction)or second position (ratio).
C)ratios can have parts added to them such as when the ratio of boys to girls in a class changes when new students add the class; common fractions cannot.
D)ratios are not independent numerical expressions and must be understood in the context of the relationships they represent; common fractions are independent of context.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
If a car uses 25 gallons of gas to travel 300 miles, which of the following ratios could be used to describe this relationship?
A)300/25 or 12 miles per gallon
B)25/300 or 0.08 gallons per mile
C)300/25 or 60 miles per 5 gallons
D)any of these answers apply
A)300/25 or 12 miles per gallon
B)25/300 or 0.08 gallons per mile
C)300/25 or 60 miles per 5 gallons
D)any of these answers apply

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
Determining the chance of rolling a prime number (3:6)on a standard six-sided die with dots ranging from 1 to 6 is an example of which of the following meaning of ratios?
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)probability relationships
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)probability relationships

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
For children to reason proportionally, they must have reached the:
A)concrete level of thinking.
B)semi-concrete level of thinking.
C)abstract level of thinking.
D)semi-abstract level of thinking.
A)concrete level of thinking.
B)semi-concrete level of thinking.
C)abstract level of thinking.
D)semi-abstract level of thinking.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
The last proportion-solving strategy that students should learn in middle school grades is using:
A)a rate table.
B)unitizing.
C)the cross-product algorithm.
D)a multiples table.
A)a rate table.
B)unitizing.
C)the cross-product algorithm.
D)a multiples table.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
Which example below uses the meaning of ratio called ratio as an operator?
A)A box of toys contains 3 airplanes and 4 toy soldiers. The ratio of airplanes to toy soldiers is 3:4.
B)Traveling at 65 miles per hour can be written as 65:1.
C)A model airplane has a scale factor of 100:1 on the box. So, if the real airplane is 200 feet long, the model would be 2 feet long.
D)If it takes 4 eggs and 3 cups of flour to make a cake, this can be stated as a 4:3 ratio of eggs to flour.
A)A box of toys contains 3 airplanes and 4 toy soldiers. The ratio of airplanes to toy soldiers is 3:4.
B)Traveling at 65 miles per hour can be written as 65:1.
C)A model airplane has a scale factor of 100:1 on the box. So, if the real airplane is 200 feet long, the model would be 2 feet long.
D)If it takes 4 eggs and 3 cups of flour to make a cake, this can be stated as a 4:3 ratio of eggs to flour.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
How could the following problem be solved on a multiples table?
Two days out of every seven days are weekend days. How many weekend days are there in 56 days?
A)Circle 2 and 5 and follow down the chart until finding to the corresponding numbers in the chart.
B)Circle 2 and 7 and follow down the chart until finding to the corresponding numbers in the chart.
C)Circle 2 and 8 and follow down the chart until finding to the corresponding numbers in the chart.
D)None of these options is correct.
Two days out of every seven days are weekend days. How many weekend days are there in 56 days?
A)Circle 2 and 5 and follow down the chart until finding to the corresponding numbers in the chart.
B)Circle 2 and 7 and follow down the chart until finding to the corresponding numbers in the chart.
C)Circle 2 and 8 and follow down the chart until finding to the corresponding numbers in the chart.
D)None of these options is correct.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
Which method of solving proportions is illustrated in the problem and solution below?
For the problem "Apples cost $2.50 for 2 pounds. How much will 9 pounds cost?" the solution process is:
Take the 2 pounds as a unit or "chunk."
Determine how much 8 pounds and 10 pounds would cost.
Determine how much the cost would be for halfway between 8 and 10 pounds.
A)using a multiples table
B)using a unit rate
C)using unitizing
D)using the cross-product algorithm
For the problem "Apples cost $2.50 for 2 pounds. How much will 9 pounds cost?" the solution process is:
Take the 2 pounds as a unit or "chunk."
Determine how much 8 pounds and 10 pounds would cost.
Determine how much the cost would be for halfway between 8 and 10 pounds.
A)using a multiples table
B)using a unit rate
C)using unitizing
D)using the cross-product algorithm

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
When teaching children about percents:
A)they must have a thorough understanding of fractions before percents are introduced.
B)they should always work with fractional denominators of 100.
C)they must have mastery of decimals before percents are introduced.
D)they should have a thorough understanding of learning aids such as base-ten materials used to introduce fractions and decimals.
A)they must have a thorough understanding of fractions before percents are introduced.
B)they should always work with fractional denominators of 100.
C)they must have mastery of decimals before percents are introduced.
D)they should have a thorough understanding of learning aids such as base-ten materials used to introduce fractions and decimals.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
π is a famous ratio relationship determined by:
A)the ratio of the diameter to the radius in a circle.
B)the ratio of the circumference to diameter in a circle.
C)the ratio of the circumference to the radius in a circle.
D)the ratio of the radius to the diameter in a circle.
A)the ratio of the diameter to the radius in a circle.
B)the ratio of the circumference to diameter in a circle.
C)the ratio of the circumference to the radius in a circle.
D)the ratio of the radius to the diameter in a circle.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
The state that Mr. Smith lives in has a 6% sales tax. If he purchases a boat that costs $16,000, he must pay $960 in taxes. The correct term associated with the $960 is referred to as the:
A)base.
B)rate.
C)percentage.
D)percent.
A)base.
B)rate.
C)percentage.
D)percent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
Which equation can be used to solve the following problem:
A tire shop sold 55% of its inventory in the last year. If it sold 2,500 tires last year, how many tires did the tire shop have in stock last year?
A)0.55 × x = 2,500
B)0.55 × 2,500 = x
C)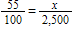
D)0.55 × x + 2,500 = 2,500 + x
A tire shop sold 55% of its inventory in the last year. If it sold 2,500 tires last year, how many tires did the tire shop have in stock last year?
A)0.55 × x = 2,500
B)0.55 × 2,500 = x
C)
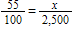
D)0.55 × x + 2,500 = 2,500 + x

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
All of the following are true about proportional reasoning except for :
A)proportional reasoning involves understanding how quantities vary in relation to each other.
B)proportional reasoning is an overarching principle of all mathematics and is central to all sub disciplines of mathematics.
C)proportional reasoning is structurally an additive relationship.
D)proportional reasoning is one of the most difficult topics for children to learn in mathematics.
A)proportional reasoning involves understanding how quantities vary in relation to each other.
B)proportional reasoning is an overarching principle of all mathematics and is central to all sub disciplines of mathematics.
C)proportional reasoning is structurally an additive relationship.
D)proportional reasoning is one of the most difficult topics for children to learn in mathematics.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
Which equation could be used to solve the problem below?
The number of students in a school increased by 150. The school originally had 500 students. By what percent did the number of students increase?
A)x % × 150 = 500
B)x % × 500 = 150
C)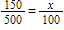
D)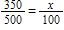
The number of students in a school increased by 150. The school originally had 500 students. By what percent did the number of students increase?
A)x % × 150 = 500
B)x % × 500 = 150
C)
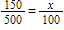
D)
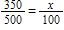

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
If Sally saw a sign in the grocery store advertising bananas for 2 lbs. for $0.85, and she needed 8 lbs., which of the following meaning of ratios would she have to use to determine the amount of money she would have to spend?
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)ratio as an operator
A)part-whole sense
B)part-part sense
C)ratio as a rate
D)ratio as an operator

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
What is the difference between a ratio and a proportion?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
Explain the differences between ratios and fractions.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
Which option shows a between proportion based on the problem below?
Five shirts require 10 yards of cloth. How many yards of cloth will 15 shirts require?
A)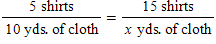
B)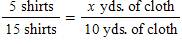
C)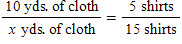
D)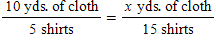
Five shirts require 10 yards of cloth. How many yards of cloth will 15 shirts require?
A)
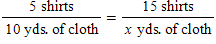
B)
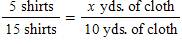
C)
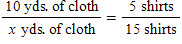
D)
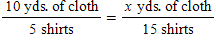

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
A pair of shoes that normally sells for $80.00 is on sale for $50.00. What is the percent discount?
A)50.0%
B)37.5%
C)30.0%
D)60.0%
A)50.0%
B)37.5%
C)30.0%
D)60.0%

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
A book that sells for $28.00 is on sale at 20% off. You also have a 10% discount to apply after the sale discount. How much will you save?
A)$20.16
B)$8.40
C)$19.60
D)$7.84
A)$20.16
B)$8.40
C)$19.60
D)$7.84

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
The tip left for a meal was $6.30. If the tip was calculated at the customary rate of 18%, what was the price of the meal?
A)$56.00
B)$44.00
C)$35.00
D)$28.00
A)$56.00
B)$44.00
C)$35.00
D)$28.00

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
Explain the difference between using the methods of unitizing and using a unit rate when working with proportional reasoning.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
In only two years the price of concert tickets increased from $25.00 to $75.00. By what percent did the tickets increase?
A)250%
B)50%
C)300%
D)200%
A)250%
B)50%
C)300%
D)200%

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
TIMSS: If the ratio of 7 to 13 is the same as the ratio of x to 52, what is the value of x ?
A)7
B)13
C)28
D)364
A)7
B)13
C)28
D)364

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
Explain the basic difference between using a rate table and using a multiples table when working with proportional reasoning.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
A sweater that originally sold for $30.00 is on sale at 20% off. After the sale, by how much must the sale price be increased to return to the pre-sale price of $30.00?
A)15%
B)20%
C)25%
D)30%
A)15%
B)20%
C)25%
D)30%

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
PISA: Trinity is in the hospital and receives an injection of penicillin. Her body gradually breaks the penicillin down so that one hour after the injection only 60% of the penicillin will remain. The pattern continues: At the end of each hour only 60% of the penicillin that was present at the end of the previous hour remains active. Suppose Trinity is given a dose of 300 milligrams of penicillin at 0800 hours. Complete this table showing the amount of penicillin that will remain active in Trinity's body at intervals of one hour from 0800 until 1100 hours.
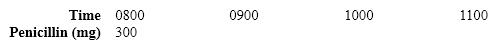
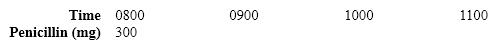

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
A Canadian dollar is worth $0.90. How much is $10.00 worth in Canadian dollars?
A)about $11.00
B)about $12.00
C)a little more than $10.00
D)about $9.00
A)about $11.00
B)about $12.00
C)a little more than $10.00
D)about $9.00

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
Explain two of the inherent difficulties students have when learning proportional reasoning.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
Competing brands of shampoo sell with the following prices:
Brand A: 12 ounces for $0.99
Brand B: 16 ounces for $1.49
Which is the better buy?
A)Brand A is a better buy.
B)Brand B is a better buy.
C)The price is the same for both brands.
D)More information is needed to solve the problem.
Brand A: 12 ounces for $0.99
Brand B: 16 ounces for $1.49
Which is the better buy?
A)Brand A is a better buy.
B)Brand B is a better buy.
C)The price is the same for both brands.
D)More information is needed to solve the problem.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
In the problem below, solve for q .
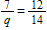
A)12
B)6
C)8⅙
D)6⅛
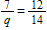
A)12
B)6
C)8⅙
D)6⅛

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
Two rectangles have similar shapes. The side lengths of one rectangle are 6 cm and 12 cm. The longer side of the second rectangle is 32 in. What is the length of the shorter side in the second rectangle?
A)26 in
B)16 in
C)16 cm
D)22 in
A)26 in
B)16 in
C)16 cm
D)22 in

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
Choose three of the meanings of ratios (part-whole sense, part-part-whole sense, relationship between two independent sets, ratio as a rate, probability relationships, or ratio as an operator)and explain the differences between them. Use examples to illustrate the differences.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the proportions below is equivalent to 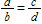
?
A)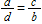
B)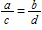
C)ac = bd
D)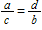
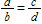
?
A)
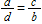
B)
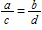
C)ac = bd
D)
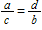

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
Teacher Licensing Examination Questions
NAEP: On the road shown below, the distance from Granville to Concord is 60 miles.

What is the distance from Granville to Princeton?
A)45 miles
B)75 miles
C)90 miles
D)105 miles
NAEP: On the road shown below, the distance from Granville to Concord is 60 miles.

What is the distance from Granville to Princeton?
A)45 miles
B)75 miles
C)90 miles
D)105 miles

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
Explain how the "cross-product algorithm" for solving proportions can degrade students' understanding of proportional relationships.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
Performance Tasks: Pattern Blocks and Tangrams
Use pattern blocks and tangrams to complete the tasks. Trace and mark your pieces to show your answers.
A square made with all seven tangram pieces is designated as one. Write the size of each of the pieces using common fractions, decimal fractions, and percent.
Use pattern blocks and tangrams to complete the tasks. Trace and mark your pieces to show your answers.
A square made with all seven tangram pieces is designated as one. Write the size of each of the pieces using common fractions, decimal fractions, and percent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
Four pattern block hexagons are equivalent to 1. Make a design in which blue pieces are ¼. Shade the pieces that represent ¼. Write the size of each of the colored pieces in your design using common fractions, decimal fractions, and percent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
A square made with all seven tangram pieces is ½. Write the size of each of the other pieces using common fractions, decimal fractions, and percent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
A square made with all seven tangram pieces is 2. Write the size of each of the other pieces using common fractions, decimal fractions, and percent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
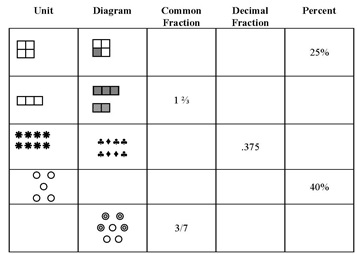
Fractional concepts may be expressed in a variety of pictorial and symbolic ways. Complete the table by filling in the missing items.


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
A teacher introduced the idea of percent by saying that it means "out of 100." Later, she wanted to have the students work with a percent greater than 100%, such as 125%. One of her students said that it is impossible to have a percent bigger than 100%, since that represents the whole. Give examples of two models that could help the teacher to clear up this confusion.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
Explain the difference between percent and percentage.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
A common misconception students have when working with similar figures in geometry is that they want to add the lengths of segments, rather than multiply. How could you convince a student that multiplication is the proper operation?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


