Deck 15: Thinking Algebraically
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/43
Play
Full screen (f)
Deck 15: Thinking Algebraically
1
The pattern below is associated with which function?
1, 2, 4, 8, 16, 32, …
A)2 n
B)2 n + 1
C)2 n
D)2 n − 1
1, 2, 4, 8, 16, 32, …
A)2 n
B)2 n + 1
C)2 n
D)2 n − 1
2 n − 1
2
The pattern below is referred to as what?
1, 8, 27, 64, …
A)square numbers
B)cubic numbers
C)Fibonacci numbers
D)pyramidal numbers
1, 8, 27, 64, …
A)square numbers
B)cubic numbers
C)Fibonacci numbers
D)pyramidal numbers
cubic numbers
3
The pattern below is referred to as what?
3, 9, 27, 81, …
A)the multiples of 3
B)the cubes of 3
C)the factors of 3
D)the powers of 3
3, 9, 27, 81, …
A)the multiples of 3
B)the cubes of 3
C)the factors of 3
D)the powers of 3
the powers of 3
4
Under what circumstance, if any, is the following statement true?
8 + 7 = 3
A)It can never be true.
B)If the equal sign were changed to a less than symbol.
C)If this were related to the number of hours on a clock.
D)If 8 and 7 were both decreased by 5.
8 + 7 = 3
A)It can never be true.
B)If the equal sign were changed to a less than symbol.
C)If this were related to the number of hours on a clock.
D)If 8 and 7 were both decreased by 5.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
5
Variable as a theme in algebra refers to:
A)finding a pattern of numbers.
B)showing the relationship between numbers.
C)a numerical representation having many possible values.
D)two numerical representations having the same value.
A)finding a pattern of numbers.
B)showing the relationship between numbers.
C)a numerical representation having many possible values.
D)two numerical representations having the same value.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
6
What is the correct domain and range for the function below?
3 n 2 - 2
A)D = {0, 1, 2} R = {−2, 1, 34}
B)D = {3, 5, 7} R = {25, 223, 339}
C)D = {2, 3, 6} R = {10, 25, 106}
D)D = {1, 4, 7} R = {1, 46, 149}
3 n 2 - 2
A)D = {0, 1, 2} R = {−2, 1, 34}
B)D = {3, 5, 7} R = {25, 223, 339}
C)D = {2, 3, 6} R = {10, 25, 106}
D)D = {1, 4, 7} R = {1, 46, 149}

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
7
The best way to get children to understand equations is to give them:
A)five examples of equations to solve.
B)balance scales to manipulate.
C)familiar formulas such as those for area.
D)nonexamples of equations, such as inequalities.
A)five examples of equations to solve.
B)balance scales to manipulate.
C)familiar formulas such as those for area.
D)nonexamples of equations, such as inequalities.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
8
Given an equation such as x + y = 18, children determine that the ordered pair (9, 9)is not possible. The most likely reason for this is:
A)they don't think that x and y can be the same number, since the variables are different.
B)they are incapable of thinking of this pair or any other ordered pair because they are not yet thinking abstractly.
C)they think that the ordered pair (10, 8)is the only possible answer.
D)they don't understand the role of the equal sign.
A)they don't think that x and y can be the same number, since the variables are different.
B)they are incapable of thinking of this pair or any other ordered pair because they are not yet thinking abstractly.
C)they think that the ordered pair (10, 8)is the only possible answer.
D)they don't understand the role of the equal sign.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
9
What is the formula for the pattern below?
1, 3, 6, 10, …
A)n + 2 n
B)n 2 + 2 n
C)n 2 + n
D)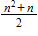
1, 3, 6, 10, …
A)n + 2 n
B)n 2 + 2 n
C)n 2 + n
D)
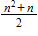

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
10
What are the next two terms of the pattern below?
2, 1, 4, 3, 6, 5, …
A)8, 7
B)7, 8
C)4, 7
D)7, 4
2, 1, 4, 3, 6, 5, …
A)8, 7
B)7, 8
C)4, 7
D)7, 4

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
11
4 y
A)a true open sentence.
B)a false open sentence.
C)an inequality with infinite numbers of values for y .
D)an equation which is true when y
A)a true open sentence.
B)a false open sentence.
C)an inequality with infinite numbers of values for y .
D)an equation which is true when y

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
12
Functions can be represented in all of the following ways except :
A)as input/output machines.
B)as tables of values.
C)as rate tables.
D)as inequalities.
A)as input/output machines.
B)as tables of values.
C)as rate tables.
D)as inequalities.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
13
Research has shown that young children:
A)are incapable of understanding the role that variables play in equation solving.
B)must have extensive practice with variables in order to understand them.
C)must have a teacher who has an extensive background in algebra in order for the teacher to help children understand variables.
D)can use variables to represent unknowns and then solve for the numbers that the variables represent.
A)are incapable of understanding the role that variables play in equation solving.
B)must have extensive practice with variables in order to understand them.
C)must have a teacher who has an extensive background in algebra in order for the teacher to help children understand variables.
D)can use variables to represent unknowns and then solve for the numbers that the variables represent.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
14
The following are true statements concerning patterning and functions except for :
A)children who are able to form patterns build a foundation for the algebraic concept of functions.
B)the ability to generalize a relationship from specific data is a hallmark of algebraic reasoning.
C)patterns follow from functions.
D)patterning is the concept of functions that is central to algebra.
A)children who are able to form patterns build a foundation for the algebraic concept of functions.
B)the ability to generalize a relationship from specific data is a hallmark of algebraic reasoning.
C)patterns follow from functions.
D)patterning is the concept of functions that is central to algebra.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
15
For younger children, the equal sign in an equation may mean all of the following except for :
A)"The answer is coming."
B)"Get ready to do something."
C)"The left side is balanced with the right side of the equation."
D)"Perform the operation on all of the numbers on the left side of the equal sign and put the result on the right side."
A)"The answer is coming."
B)"Get ready to do something."
C)"The left side is balanced with the right side of the equation."
D)"Perform the operation on all of the numbers on the left side of the equal sign and put the result on the right side."

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is not a function?
A){(A, 1), (B, 2), (C, 3)}
B){(A, 1), (B, 1), (C, 3)}
C){(A, 1), (B, 2), (B, 3), (C, 1), (C, 2)}
D){(A, 2), (B, 2), (C, 2)}
A){(A, 1), (B, 2), (C, 3)}
B){(A, 1), (B, 1), (C, 3)}
C){(A, 1), (B, 2), (B, 3), (C, 1), (C, 2)}
D){(A, 2), (B, 2), (C, 2)}

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
17
Algebra in elementary school is best understood as:
A)a simplified version of high school algebra.
B)focusing on the finding and extending of patterns.
C)pre-algebra.
D)a natural extension of other content standards.
A)a simplified version of high school algebra.
B)focusing on the finding and extending of patterns.
C)pre-algebra.
D)a natural extension of other content standards.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
18
Young children can best learn about functions in all of the following ways except for :
A)exploring function relationships.
B)working with the definition of functions.
C)solving function problems.
D)applying functions to real-life situations.
A)exploring function relationships.
B)working with the definition of functions.
C)solving function problems.
D)applying functions to real-life situations.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
19
When teaching patterns to young children, teachers should emphasize:
A)finding, extending, and making different patterns.
B)limiting instruction to one or two examples to decrease confusion.
C)limiting instruction to only those patterns children are likely to be familiar with.
D)the algebraic aspect of patterning.
A)finding, extending, and making different patterns.
B)limiting instruction to one or two examples to decrease confusion.
C)limiting instruction to only those patterns children are likely to be familiar with.
D)the algebraic aspect of patterning.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
20
What are the next three numbers in the pattern below?
2, 6, 12, 20, 30, …
A)44, 52, 64
B)40, 50, 60
C)42, 54, 63
D)42, 56, 72
2, 6, 12, 20, 30, …
A)44, 52, 64
B)40, 50, 60
C)42, 54, 63
D)42, 56, 72

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose that t = the number of tiles in a problem-solving situation, and a child tells you that 3 t means 3 tiles. How can you explain to him that his reasoning is faulty?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
22
What is the inherent difficulty children have when working with an equation such as a + b = 12?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
23
Give three specific examples of different types of patterns that a teacher can use to introduce algebraic ideas to young children.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
24
PISA: The illustration below shows the footprints of a man walking.

The pace length, p , is the distance between the rear of two consecutive footprints.
For men, the formula n / p = 140 gives an approximate relationship between n and p where
n = number of steps per minute, and
p = pace length in meters
If the formula applies to Heiko's walking and Heiko takes 70 steps per minute, what is Heiko's pace length? Be sure to show your work.

The pace length, p , is the distance between the rear of two consecutive footprints.
For men, the formula n / p = 140 gives an approximate relationship between n and p where
n = number of steps per minute, and
p = pace length in meters
If the formula applies to Heiko's walking and Heiko takes 70 steps per minute, what is Heiko's pace length? Be sure to show your work.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
25
Solve for n in the equation below.
4 n + 6 = 3 n + 10 + n - 2
A)n = 2
B)n = 3
C)n = all values
D)no solution
4 n + 6 = 3 n + 10 + n - 2
A)n = 2
B)n = 3
C)n = all values
D)no solution

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
26
NAEP: The terms in this sequence are the squares of consecutive odd numbers:
1, 9, 25, 49, 81, …
The same rule is applied to each number in the given pattern. What is the sixth number in the pattern?
A)40
B)100
C)121
D)144
1, 9, 25, 49, 81, …
The same rule is applied to each number in the given pattern. What is the sixth number in the pattern?
A)40
B)100
C)121
D)144

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
27
Teacher Licensing Examination Questions
Praxis: If 4 x − 3( x + 1)= 5, what is the value of x ?
A)2
B)4
C)6
D)8
Praxis: If 4 x − 3( x + 1)= 5, what is the value of x ?
A)2
B)4
C)6
D)8

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
28
The series below is composed of triangular number. What is the next term in the series?
1, 3, 6, 10, …
A)14
B)13
C)15
D)16
1, 3, 6, 10, …
A)14
B)13
C)15
D)16

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
29
A newspaper carrier was offered the chance to earn $0.01 on the first day of a month, $0.02 on the second day, and so forth doubling every day. How much did the carrier get paid at the end of the second week?
A)about $160.00
B)about $20.00
C)about $40.00
D)about $80.00
A)about $160.00
B)about $20.00
C)about $40.00
D)about $80.00

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
30
Given the value for n , what is the function that produces the following data? 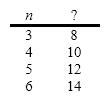
A)2 n
B)2 n + 2
C)n + 1
D)3 n - 1

A)2 n
B)2 n + 2
C)n + 1
D)3 n - 1

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
31
What are some specific ways that a teacher can introduce the idea of variables without actually using letters for variables?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
32
What is the major difference in the role that the variable plays in the equation 6 x = 30 and the inequality 6 x > 30? What difficulties do children have with respect to the inequality?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
33
Explain the role that patterning plays in helping develop children's algebraic reasoning.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
34
In this pattern, what is the value of p when n = 10? 
A)15
B)60
C)50
D)55

A)15
B)60
C)50
D)55

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
35
What is the next term in the pattern below?
A, d, g, j…
A)k
B)n
C)l
D)m
A, d, g, j…
A)k
B)n
C)l
D)m

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
36
Using patterns, what is the number of diagonals in an undecagon (11 sides)?
A)40
B)42
C)44
D)46
A)40
B)42
C)44
D)46

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
37
Solve for n in the equation below.
3 n + 6 = n + 8 + 2 n - 2
A)n = 2
B)n = 3
C)n = all values
D)no solution
3 n + 6 = n + 8 + 2 n - 2
A)n = 2
B)n = 3
C)n = all values
D)no solution

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
38
The pattern below is called the Fibonacci sequence. What is the next term in the pattern?
1, 1, 2, 3, 5, 8, …
A)11
B)13
C)12
D)14
1, 1, 2, 3, 5, 8, …
A)11
B)13
C)12
D)14

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
39
Using clock arithmetic, what is 6 + 7 = ?
A)11
B)12
C)1
D)2
A)11
B)12
C)1
D)2

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
40
TIMSS: n is a number. When n is multiplied by 7 and then 6 is added, the result is 41. Which of these equations represents this relation?
A)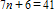
B)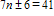
C)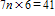
D)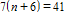
A)
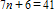
B)
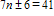
C)
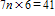
D)
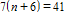

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
41
Explain some of the difficulties children have with understanding the role of the equal sign in equations.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose you wanted to teach children to solve equations, and you have the following examples:
8 - t = 2
x + 3 = 7
___ + 5 = 6
6 + r = 13
m - 4 = 5
Place the equations in the order you think would be best in order for the children to understand the concept of equations. Explain your decision.
8 - t = 2
x + 3 = 7
___ + 5 = 6
6 + r = 13
m - 4 = 5
Place the equations in the order you think would be best in order for the children to understand the concept of equations. Explain your decision.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
43
A child asks you what a function is. Give several specific examples that you would use to explain this important algebraic concept to her.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck


