Deck 19: Investigating Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/47
Play
Full screen (f)
Deck 19: Investigating Probability
1
Theoretical probability is the same as:
A)empirical probability.
B)historical probability.
C)mathematical probability.
D)experimental probability.
A)empirical probability.
B)historical probability.
C)mathematical probability.
D)experimental probability.
mathematical probability.
2
Sundaes at an ice cream shop have either vanilla or chocolate ice cream; marshmallow, strawberries, or hot fudge for toppings; and either a cherry or peanuts as a garnish. How many sundae combinations are possible?
A)7
B)12
C)24
D)cannot be determined
A)7
B)12
C)24
D)cannot be determined
12
3
A bag has 6 green marbles and 3 blue marbles. You pick out a blue marble. If you do not put the marble back, what is the probability of now selecting a green marble?
A)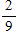
B)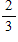
C)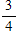
D)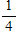
A)
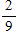
B)
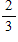
C)
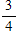
D)
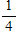
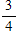
4
What is the odds in favor of rolling a 7 with a pair of dice?
A)6:36
B)6:30
C)30:6
D)36:6
A)6:36
B)6:30
C)30:6
D)36:6

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
5
All of the following are true of a fair spinner except that it:
A)spins the same way every time.
B)is completely random.
C)can stop any place on the spinner face.
D)treats all students the same way.
A)spins the same way every time.
B)is completely random.
C)can stop any place on the spinner face.
D)treats all students the same way.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
6
When conducting a sample of a population:
A)a sample equivalent to half the population must be drawn in order to make any inferences about the given population.
B)the entire population must be sampled to get accurate results .
C)a relatively small random sample will be sufficient to make inferences about the entire population.
D)multiple random samples must be drawn in order to make inferences about the entire population.
A)a sample equivalent to half the population must be drawn in order to make any inferences about the given population.
B)the entire population must be sampled to get accurate results .
C)a relatively small random sample will be sufficient to make inferences about the entire population.
D)multiple random samples must be drawn in order to make inferences about the entire population.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
7
What is the probability that a day in the month of March has a 2 in it?
A)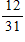
B)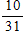
C)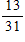
D)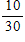
A)
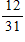
B)
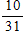
C)
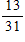
D)
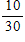

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is a true statement concerning probability values?
A)The probability of an event ranges between 0 and 1.
B)The probability of an impossible event can be negative.
C)The probability of a certain event can be 1.2.
D)0 P ( x )1, where P ( x )stands for the probability of event x happening.
A)The probability of an event ranges between 0 and 1.
B)The probability of an impossible event can be negative.
C)The probability of a certain event can be 1.2.
D)0 P ( x )1, where P ( x )stands for the probability of event x happening.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
9
Determining the probability that your insurance rates will be higher than others is based on:
A)mathematical probability.
B)historical probability.
C)both mathematical and historical probability.
D)neither mathematical nor historical probability.
A)mathematical probability.
B)historical probability.
C)both mathematical and historical probability.
D)neither mathematical nor historical probability.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
10
The law of large numbers stipulates that
A)the greater the number of events that occur for a particular situation, the closer to the theoretical probability the results will be.
B)the fewer the number of events that occur for a particular situation, the closer to the theoretical probability the results will be.
C)the greater the number of events that occur for a particular situation, the farther away from the theoretical probability the results will be.
D)the fewer the number of events that occur for a particular situation, the farther away from the theoretical probability the results will be.
A)the greater the number of events that occur for a particular situation, the closer to the theoretical probability the results will be.
B)the fewer the number of events that occur for a particular situation, the closer to the theoretical probability the results will be.
C)the greater the number of events that occur for a particular situation, the farther away from the theoretical probability the results will be.
D)the fewer the number of events that occur for a particular situation, the farther away from the theoretical probability the results will be.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
11
A 40% chance of snow means the probability of snow is:
A)40
B)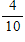
C)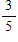
D)4
A)40
B)
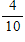
C)
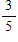
D)4

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
12
What is the probability of rolling a 6 with a pair of dice?
A)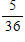
B)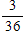
C)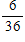
D)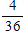
A)
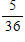
B)
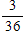
C)
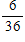
D)
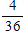

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
13
What is the sum of the numbers in the fourth row of Pascal's Triangle?
A)2
B)4
C)6
D)8
A)2
B)4
C)6
D)8

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
14
A student took the letters M, A, T and wrote down the possibilities MAT, MTA, TAM, TMA, ATM, AMT from the given three letters. When the student wrote out the 6 possibilities, he was finding the
A)empirical probability.
B)historical probability.
C)combinations of M, A, T.
D)permutations of M, A, T.
A)empirical probability.
B)historical probability.
C)combinations of M, A, T.
D)permutations of M, A, T.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
15
Empirical probability is used in which of the following?
A)lottery
B)slot machines
C)roulette
D)insurance rates
A)lottery
B)slot machines
C)roulette
D)insurance rates

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
16
A fair spinner with four colors on its face must have the following be true except:
A)The areas of each color must be equal.
B)The spinner will land randomly anywhere on the face.
C)There is only one region for each color.
D)All of these answers must be true.
A)The areas of each color must be equal.
B)The spinner will land randomly anywhere on the face.
C)There is only one region for each color.
D)All of these answers must be true.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose a spinner is divided into 4 areas: $6 (geometric probability of ½), $4 (geometric probability of ¼), $2 (geometric probability of ⅛ for each ⅛ section). How much would an organization have to charge in order to break even?
A)$4.00
B)$4.50
C)$5.00
D)$5.50
A)$4.00
B)$4.50
C)$5.00
D)$5.50

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
18
Children who are susceptible to the gambler's fallacy believe that:
A)they are guaranteed to win again if they win once .
B)they are due for a tail on the next coin toss if they have a streak of 10 heads .
C)the longer they play a game, the worse their chances of winning.
D)they won't lose something they've won if they keep playing.
A)they are guaranteed to win again if they win once .
B)they are due for a tail on the next coin toss if they have a streak of 10 heads .
C)the longer they play a game, the worse their chances of winning.
D)they won't lose something they've won if they keep playing.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
19
The outcome when tossing one coin is (H, T). The outcome when tossing two coins is (HH, HT, TH, TT). The outcome when tossing three coins is (HHH, HHT, HTH, THH, TTH, THT, HTT, TTT). This pattern of outcomes can be mapped to:
A)the Fibonacci numbers.
B)the square numbers.
C)Pascal's Triangle.
D)the multiples of two.
A)the Fibonacci numbers.
B)the square numbers.
C)Pascal's Triangle.
D)the multiples of two.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
20
Simulations are used to determine the probability of an event in all of the following situations except for :
A)when there are no data from previous events.
B)when it is not possible to gather experimental data of the event.
C)when the theoretical probability is impossible to compute.
D)when the theoretical probability is available.
A)when there are no data from previous events.
B)when it is not possible to gather experimental data of the event.
C)when the theoretical probability is impossible to compute.
D)when the theoretical probability is available.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
21
Explain the differences between historical and mathematical probability.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
22
The entire target of a bull's eye is enlarged by a factor of 3. The new chance of hitting the bull's eye:
A)remains the same.
B)is tripled.
C)is increased by a factor of 9.
D)is decreased by ⅓.
A)remains the same.
B)is tripled.
C)is increased by a factor of 9.
D)is decreased by ⅓.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
23
Explain how someone who plays the same slot machine for hours on end has fallen prey to the Gambler's Fallacy.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
24
Probability plays a role in each of the following games except:
A)Candy Land.
B)Chess.
C)Monopoly.
D)Chutes and Ladders.
A)Candy Land.
B)Chess.
C)Monopoly.
D)Chutes and Ladders.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
25
For all probabilities ( p ), which option is correct?
A) p < 1
B) 0 < p
C) 0 < p < 1
D) 0 ≤ p ≤ 1
A) p < 1
B) 0 < p
C) 0 < p < 1
D) 0 ≤ p ≤ 1

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
26
The chance of rain is 60%. What are the odds in favor of rain?
A)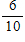
B)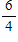
C)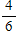
D)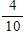
A)
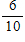
B)
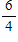
C)
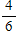
D)
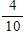

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
27
A hitter in baseball with a 0.300 average has which probability of getting a hit?
A)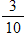
B)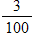
C)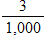
D)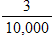
A)
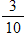
B)
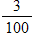
C)
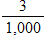
D)
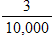

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
28
NAEP: There are 15 girls and 11 boys in a mathematics class. If a student is selected at random to run an errand, what is the probability that a boy will be selected?
A)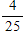
B)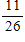
C)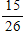
D)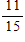
A)
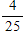
B)
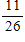
C)
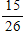
D)
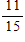

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
29
Teacher Licensing Examination Questions
Praxis: A two-sided coin is unfairly weighted so that when it is tossed, the probability that heads will result is twice the probability that tails will result. If the coin is to be tossed three separate times, what is the probability that tails will result on exactly two of the tosses?
A)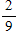
B)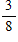
C)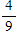
D)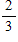
Praxis: A two-sided coin is unfairly weighted so that when it is tossed, the probability that heads will result is twice the probability that tails will result. If the coin is to be tossed three separate times, what is the probability that tails will result on exactly two of the tosses?
A)
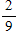
B)
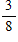
C)
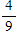
D)
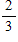

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
30
TIMSS: In a school there were 1,200 students (boys and girls). A sample of 100 students was selected at random, and 45 boys were found in the sample. Which of these is most likely to be the number of boys in the school?
A)450
B)500
C)540
D)600
A)450
B)500
C)540
D)600

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
31
How would you explain to a young child what probability is?

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
32
Explain the role that calculators and computer software play in teaching probability. Give specific examples.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
33
PISA: A documentary was broadcast about earthquakes and how often they occur. It included a discussion about the predictability of earthquakes. A geologist stated: "In the next twenty years, the chance that an earthquake will occur in Zed City is two out of three." Which of the following best reflects the meaning of the geologist's statement ?
A)⅔ × 20 = 13.3, so between 13 and 14 years from now there will be an earthquake in Zed City.
B)⅔ is more than ½, so you can be sure there will be an earthquake in Zed City.
C)The likelihood that there will be an earthquake in Zed City at some time during the next 20 years is higher than the likelihood of no earthquake.
D)You cannot tell what will happen, because nobody can be sure when an earthquake will occur.
A)⅔ × 20 = 13.3, so between 13 and 14 years from now there will be an earthquake in Zed City.
B)⅔ is more than ½, so you can be sure there will be an earthquake in Zed City.
C)The likelihood that there will be an earthquake in Zed City at some time during the next 20 years is higher than the likelihood of no earthquake.
D)You cannot tell what will happen, because nobody can be sure when an earthquake will occur.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
34
The probability of an event can be determined by:
A)theoretical probability.
B)simulation.
C)experimental probability.
D)all of these options.
A)theoretical probability.
B)simulation.
C)experimental probability.
D)all of these options.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
35
Give examples that will help children understand the terms impossible, unlikely, likely, and certain as they pertain to the probability of events happening.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
36
Explain what the law of large numbers says, and explain how you would implement it when teaching probability.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
37
What is the probability of flipping a coin to get 3 tails in a row?
A)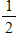
B)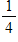
C)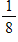
D)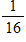
A)
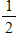
B)
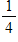
C)
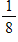
D)
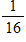

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
38
In a school with 2,400 students, a random sample of 100 students included 45 boys. Based on this sample, how many boys attend the school?
A)860
B)100
C)1,080
D)1,200
A)860
B)100
C)1,080
D)1,200

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
39
What is the probability a tossed coin will land in a designated square on a chessboard?
A)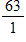
B)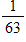
C)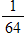
D)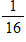
A)
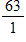
B)
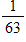
C)
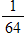
D)
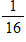

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
40
Candace flipped a coin 10 times and recorded 3 heads and 7 tails. She claims her coin is not a fair coin. She is forgetting to apply:
A)the Gambler's Fallacy.
B)historical probability.
C)the law of Large Numbers.
D)the Monte Carlo Method.
A)the Gambler's Fallacy.
B)historical probability.
C)the law of Large Numbers.
D)the Monte Carlo Method.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
41
Explain the connection between tossing coins and Pascal's Triangle.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
42
Explain how a national survey of only 400 people can be valid.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
43
Design a target that has the following probabilities for hitting various shapes:
Square 20%
Rectangle 10%
Triangle 25%
Background 45%
Square 20%
Rectangle 10%
Triangle 25%
Background 45%

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
44
Display the face of a spinner that has the following theoretical probabilities:
1 - 25%
2 - 50%
3 - 12.5%
4 - 12.5%
1 - 25%
2 - 50%
3 - 12.5%
4 - 12.5%

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
45
Design an activity to determine the probability of a toothpaste cap landing right side up when flipped into the air.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
46
Show the probability tree for the permutations for the letters A R T.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck
47
Design an expected value experiment using geometric probability. Explain how your experiment yields the expected value.

Unlock Deck
Unlock for access to all 47 flashcards in this deck.
Unlock Deck
k this deck


