Deck 21: Supplement D Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/87
Play
Full screen (f)
Deck 21: Supplement D Linear Programming
1
A parameter is a region that represents all permissible combinations of the decision variables in a linear programming model.
False
2
A manufacturer builds finished items A, B, and C from five different components. They currently have several finished units, a number of items that are partially complete, and many components that have just been delivered from their suppliers. The finished items, incomplete items and raw components can all be assigned some monetary value even though the manufacturer typically does not sell anything except finished items. The manufacturer needs to raise capital quickly so they formulate a linear program to help them decide on the most profitable way ahead. Their linear programming expert forgets to restrict their decision variables to non-negative values and is surprised when the computer output tells them that finished item A and C should be negative. If the company always follows the advice of their linear programming analysis, what should they do and why?
The assumption of nonnegativity is that decision variables must either be positive or zero. In this case, it would appear that either A) the components are more valuable to the company than the finished items (perhaps there is a pricing error and the company is not charging enough for their products) or B) disassembling items A and C might yield parts that could be used to produce item B, which is a more profitable product. Depending on the values of the other decision variable, the company should begin disassembly of finished items A and C. They might also ask their linear programming analyst to update his resume.
3
Decision variables are represented in both the objective function and the constraints while formulating a linear program.
True
4
A(n) ________ is a value that the decision maker cannot control and that does not change when the solution is implemented.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
5
________ is an assumption that the decision variables must be either positive or zero.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
6
What are the assumptions of linear programming? Provide examples of each.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
7
In linear programming, each parameter is assumed to be known with certainty.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
8
The objective function Maximize Z = 3x² ⁺ ⁴ʸ is appropriate for linear programming.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
9
________ is useful for allocating scarce resources among competing demands.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
10
The assumption of ________ allows a decision maker to combine the profit from one product with the profit from another to realize the total profit from a feasible solution.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
11
An = (equal to) constraint is often used for certain mandatory relationships.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
12
One assumption of linear programming is that a decision maker cannot use negative quantities of the parameters.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
13
Linear programming is useful for allocating scarce resources among competing demands.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
14
The ________ represents all permissible combinations of the decision variables in a linear programming model.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
15
In a linear program, ________ represent choices the decision maker can control.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
16
In a linear program, ________ are the limitations that restrict the permissible choices for the decision variables.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
17
Parameters that are quantified without doubt meet the linear programming assumption of ________.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
18
The ________ is an expression in linear programming models that states mathematically what is being maximized or minimized.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following statements regarding linear programming is best?
A) A parameter is also known as a decision variable.
B) Linearity assumes proportionality and additivity.
C) Since nonnegativity is required, parameters must be greater than or equal to zero.
D) Linear programming ensures the decision maker will reach a single, optimal solution.
A) A parameter is also known as a decision variable.
B) Linearity assumes proportionality and additivity.
C) Since nonnegativity is required, parameters must be greater than or equal to zero.
D) Linear programming ensures the decision maker will reach a single, optimal solution.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
20
A manager is interested in using linear programming to analyze production for the ensuing week. She knows that it will take exactly 1.5 hours to run a batch of product A and that this batch will consume two tons of sugar. This is an example of the linear programming assumption of:
A) linearity.
B) certainty.
C) continuous variables.
D) whole numbers.
A) linearity.
B) certainty.
C) continuous variables.
D) whole numbers.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
21
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate constraint for this scenario?
A) 4*Eggs + 5*Tomatoes + 14*Chicken ≥ 15
B) 22*Protein + 15*VitaminA + 8*VitaminB ≥ 8
C) )12*Egg + .5*Tomato + .4*Chicken ≥ 4
D) 22*Protein + 15*VitaminA + 8*VitaminB ≥ 4
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate constraint for this scenario?
A) 4*Eggs + 5*Tomatoes + 14*Chicken ≥ 15
B) 22*Protein + 15*VitaminA + 8*VitaminB ≥ 8
C) )12*Egg + .5*Tomato + .4*Chicken ≥ 4
D) 22*Protein + 15*VitaminA + 8*VitaminB ≥ 4

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
22
The ________ problem is a one-period type of aggregate planning problem, the solution of which yields optimal output quantities of a group of products or services, subject to resource capacity and market demand conditions.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
23
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, assume that an optimal serving contains 0.89 ounces of chicken and 0.52 ounces of tomatoes. Which of the following statements is best?
A) The serving costs about 20 cents.
B) The serving costs about 30 cents
C) The serving costs about 40 cents.
D) The serving costs about 50 cents.
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, assume that an optimal serving contains 0.89 ounces of chicken and 0.52 ounces of tomatoes. Which of the following statements is best?
A) The serving costs about 20 cents.
B) The serving costs about 30 cents
C) The serving costs about 40 cents.
D) The serving costs about 50 cents.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
24
When plotting constraints, it is best to ignore the inequality aspect of the equation.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
25
An equality constraint requires that only the points on the line described by the constraint are feasible.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
26
Belsky Manufacturing makes three models of fans, identified by the unimaginative names of A, B, and C. The fans are made out of nuts, bolts, wire, blades, and motors. The current inventory levels and parts list for each type of fan is shown in the table.
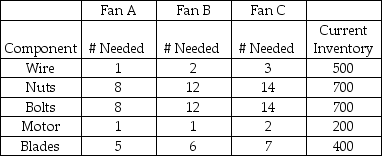
Fan A sells for $18, Fan B sells for $25, and Fan C sells for $30. Formulate this decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.

Fan A sells for $18, Fan B sells for $25, and Fan C sells for $30. Formulate this decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
27
A producer has three products, A, B, and C, which are composed from many of the same raw materials and subassemblies by the same skilled workforce. Each unit of product A uses 15 units of raw material X, a single purge system subassembly, a case, a power cord, three labor hours in the assembly department, and one labor hour in the finishing department. Each unit of product B uses 10 units of raw material X, five units of raw material Y, two purge system subassemblies, a case, a power cord, five labor hours in the assembly department, and 90 minutes in the finishing department. Each unit of product C uses five units of raw material X, 25 units of raw material Y, two purge system subassemblies, a case, a power cord, seven labor hours in the assembly department, and three labor hours in the finishing department. Labor between the assembly and finishing departments is not transferable, but workers within each department work on any of the three products. There are three full-time (40 hours/week) workers in the assembly department and one full-time and one half-time (20 hours/week) worker in the finishing department. At the start of this week, the company has 300 units of raw material X, 400 units of raw material Y, 60 purge system subassemblies, 40 cases, and 50 power cords in inventory. No additional deliveries of raw materials are expected this week. There is a $90 profit on product A, a $120 profit on product B, and a $150 profit on product C. The operations manager doesn't have any firm orders, but would like to make at least five of each product so he can have the products on the shelf in case a customer wanders in off the street.
Formulate the objective function and all constraints, and clearly identify each constraint by the name of the resource or condition it represents.
Formulate the objective function and all constraints, and clearly identify each constraint by the name of the resource or condition it represents.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
28
A binding constraint has slack but does not have surplus.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
29
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate constraint for this scenario?
A) 4*Eggs + 8*Tomatoes + 14*Chicken ≤ 15
B) 5*Eggs + 1*Tomatoes + 22*Chicken ≥ 20
C) 4*Eggs + 8*Tomatoes + 14*Chicken = 15
D) 15*VitaminA = Eggs + Tomatoes + Chicken
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate constraint for this scenario?
A) 4*Eggs + 8*Tomatoes + 14*Chicken ≤ 15
B) 5*Eggs + 1*Tomatoes + 22*Chicken ≥ 20
C) 4*Eggs + 8*Tomatoes + 14*Chicken = 15
D) 15*VitaminA = Eggs + Tomatoes + Chicken

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
30
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate objective function for this scenario?
A) Max Z = .12*Egg + .08*Tomato + .4*Chicken
B) Max Z = 20*Protein + 15*VitaminA + 10*VitaminB
C) Min Z = .12*Egg + .08*Tomato + .4*Chicken
D) Min Z = 20*Protein + 15*VitaminA + 10*VitaminB
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, what is an appropriate objective function for this scenario?
A) Max Z = .12*Egg + .08*Tomato + .4*Chicken
B) Max Z = 20*Protein + 15*VitaminA + 10*VitaminB
C) Min Z = .12*Egg + .08*Tomato + .4*Chicken
D) Min Z = 20*Protein + 15*VitaminA + 10*VitaminB

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
31
Case: 1A + 1B + 1C ≤ 40
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 22 units of protein, 15 units of vitamin A, and 8 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 6 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 8 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 8 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 5 cents per ounce, and eggs cost 12 cents per ounce. To make the production process as easy as possible, she would like to make exactly four ounces of cat food from her recipe. Formulate this decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 22 units of protein, 15 units of vitamin A, and 8 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 6 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 8 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 8 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 5 cents per ounce, and eggs cost 12 cents per ounce. To make the production process as easy as possible, she would like to make exactly four ounces of cat food from her recipe. Formulate this decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
32
The graphical method is a practical method for solving product mix problems of any size, provided the decision maker has sufficient quantities of graph paper.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
33
The terms slack and surplus both refer to having too much of a resource.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
34
Only corner points should be considered for the optimal solution to a linear programming problem.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
35
Case: 1A + 1B + 1C ≤ 40
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
A portfolio manager is trying to balance investments between bonds, stocks and cash. The return on stocks is 12 percent, 9 percent on bonds, and 3 percent on cash. The total portfolio is $1 billion, and he or she must keep 10 percent in cash in accordance with company policy. The fund's prospectus promises that stocks cannot exceed 75 percent of the portfolio, and the ratio of stocks to bonds must equal two. Formulate this investment decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
A portfolio manager is trying to balance investments between bonds, stocks and cash. The return on stocks is 12 percent, 9 percent on bonds, and 3 percent on cash. The total portfolio is $1 billion, and he or she must keep 10 percent in cash in accordance with company policy. The fund's prospectus promises that stocks cannot exceed 75 percent of the portfolio, and the ratio of stocks to bonds must equal two. Formulate this investment decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
36
Case: 1A + 1B + 1C ≤ 40
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
NYNEX must schedule round-the-clock coverage for its telephone operators. To keep the number of different shifts down to a manageable level, it has only four different shifts. Operators work eight-hour shifts and can begin work at either midnight, 8 a.m., noon, or 4 p.m. Operators are needed according to the following demand pattern, given in four-hour time blocks.
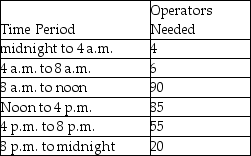
Formulate this scheduling decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.
Cord: 1A + 1B + 1C ≤ 50
Assembly Department Labor: 3A + 5B + 7C ≤ 120
Finish Department Labor: 1A + 1.5B + 3C ≤ 60
Minimum Production for A: 1A + 0B + 0C ≥ 5
Minimum Production for B: 0A + 1B + 0C ≥ 5
Minimum Production for C: 0A + 0B + 1C ≥ 5
NYNEX must schedule round-the-clock coverage for its telephone operators. To keep the number of different shifts down to a manageable level, it has only four different shifts. Operators work eight-hour shifts and can begin work at either midnight, 8 a.m., noon, or 4 p.m. Operators are needed according to the following demand pattern, given in four-hour time blocks.

Formulate this scheduling decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
37
Belsky Manufacturing makes three models of fans, identified by the unimaginative names of A, B, and C. The fans are made out of nuts, bolts, wire, blades, and motors. The current inventory levels and parts list for each type of fan is shown in the table.
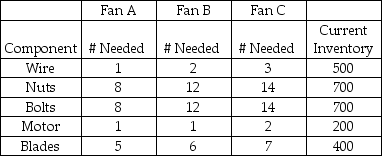
Fan A sells for $18, Fan B sells for $25, and Fan C sells for $30.
Milo Belsky decided to arrive at an optimal production quantity using linear programming. His initial solution was to produce 50 Fan As and 21.4 Fan Cs for a profit of $1,542.86.
Determine what his inventory would be.
Charlie Belsky made an important change to the model and ran the linear programming software again, His solution was to produce 50 Fan As, -150 Fan Bs, and 150 Fan Cs for a profit of $1,650 units. What change did he make to the model and what would the ending inventory be if they were to produce according to this plan? What are the practical implications of this solution?

Fan A sells for $18, Fan B sells for $25, and Fan C sells for $30.
Milo Belsky decided to arrive at an optimal production quantity using linear programming. His initial solution was to produce 50 Fan As and 21.4 Fan Cs for a profit of $1,542.86.
Determine what his inventory would be.
Charlie Belsky made an important change to the model and ran the linear programming software again, His solution was to produce 50 Fan As, -150 Fan Bs, and 150 Fan Cs for a profit of $1,650 units. What change did he make to the model and what would the ending inventory be if they were to produce according to this plan? What are the practical implications of this solution?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
38
Which of the following statements regarding linear programming is not True?
A) A linear programming problem can have more than one optimal solution.
B) Most real-world linear programming problems are solved on a computer.
C) If a binding constraint were relaxed, the optimal solution wouldn't change.
D) A surplus variable is added to a > constraint to convert it to an equality.
A) A linear programming problem can have more than one optimal solution.
B) Most real-world linear programming problems are solved on a computer.
C) If a binding constraint were relaxed, the optimal solution wouldn't change.
D) A surplus variable is added to a > constraint to convert it to an equality.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
39
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, which of the following statements is best?
A) Making the cat food out of only eggs is optimal
B) Making the cat food out of only eggs is less expensive than making it out of only tomatoes.
C) Making the cat food out of only eggs means that the Vitamin B constraint would not be satisfied.
D) Making the cat food out of only chicken means the Vitamin B constraint would not be satisfied.
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
Referring to Scenario D.1, which of the following statements is best?
A) Making the cat food out of only eggs is optimal
B) Making the cat food out of only eggs is less expensive than making it out of only tomatoes.
C) Making the cat food out of only eggs means that the Vitamin B constraint would not be satisfied.
D) Making the cat food out of only chicken means the Vitamin B constraint would not be satisfied.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
40
In a linear programming model, the objective function answers the question What is to be maximized?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
41
________ is the amount by which the left-hand side falls short of the right-hand side in a linear programming model.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
42
Briefly describe the meaning of a shadow price. Provide an example of how a manager could use information about shadow prices to improve operations?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
43
In linear programming, a(n) ________ is a point that lies at the intersection of two (or possibly more) constraint lines on the boundary of the feasible region.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
44
You observe a linear programming problem that has been solved using the graphical method of linear programming. The feasible region and optimal solution are clearly labeled. How could you identify the slack or surplus amounts in the scenario?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
45
Use the graphical technique to find the optimal solution for this objective function and associated constraints.
Maximize: Z = 8A + 5B
Subject To:
Constraint 1 4A + 5B < 80
Constraint 2 7A + 4B < 120
A, B > 0
Graph the problem fully in the following space. Label the axes carefully, plot the constraints, shade the feasibility region, identify all candidate corner points, and indicate which one yields the optimal answer.
Maximize: Z = 8A + 5B
Subject To:
Constraint 1 4A + 5B < 80
Constraint 2 7A + 4B < 120
A, B > 0
Graph the problem fully in the following space. Label the axes carefully, plot the constraints, shade the feasibility region, identify all candidate corner points, and indicate which one yields the optimal answer.


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
46
Consider a corner point to a linear programming problem, which lies at the intersection of the following two constraints: 6X₁ + 15X₂ < 390
2X₁ + X₂ < 50
Which of the following statements about the corner point is True?
A) X₁ < 21
B) X₁ > 25
C) X₁ < 10
D) X₁ > 17
2X₁ + X₂ < 50
Which of the following statements about the corner point is True?
A) X₁ < 21
B) X₁ > 25
C) X₁ < 10
D) X₁ > 17

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
47
In a linear programming model formulation, what does the feasible region represent?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
48
For the line that has the equation 4X₁ + 8X₂ = 88, an axis intercept is:
A) (0, 22).
B) (6, 0).
C) (6, 22).
D) (0, 11).
A) (0, 22).
B) (6, 0).
C) (6, 22).
D) (0, 11).

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
49
________ is the amount by which the left-hand side exceeds the right-hand side in a linear programming model.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
50
The ________ is the upper and lower limit of an objective function coefficient over which the optimal values of the decision variables remain unchanged.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
51
A modeler is limited to two or fewer decision variables when using the ________.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
52
A manager is interested in deciding production quantities for products A, B, and C. He has an inventory of 20 tons each of raw materials 1, 2, 3, and 4 that are used in the production of products A, B, and C. He can further assume that he can sell all of what he makes. Which of the following statements is correct?
A) The manager has four decision variables.
B) The manager has three constraints.
C) The manager has three decision variables.
D) The manager can solve this problem graphically.
A) The manager has four decision variables.
B) The manager has three constraints.
C) The manager has three decision variables.
D) The manager can solve this problem graphically.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
53
You are faced with a linear programming objective function of: Max P = $20X + $30Y
And constraints of:
3X + 4Y = 24 (Constraint A)
5X - Y = 18 (Constraint B)
You discover that the shadow price for Constraint A is 7.5 and the shadow price for Constraint B is 0. Which of these statements is True?
A) You can change quantities of X and Y at no cost for Constraint B.
B) For every additional unit of the objective function you create, you lose 0 units of B.
C) For every additional unit of the objective function you create, the price of A rises by $7.50.
D) The most you would want to pay for an additional unit of A would be $7.50.
And constraints of:
3X + 4Y = 24 (Constraint A)
5X - Y = 18 (Constraint B)
You discover that the shadow price for Constraint A is 7.5 and the shadow price for Constraint B is 0. Which of these statements is True?
A) You can change quantities of X and Y at no cost for Constraint B.
B) For every additional unit of the objective function you create, you lose 0 units of B.
C) For every additional unit of the objective function you create, the price of A rises by $7.50.
D) The most you would want to pay for an additional unit of A would be $7.50.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
54
While glancing over the sensitivity report, you note that the stitching labor has a shadow price of $10 and a lower limit of 24 hours with an upper limit of 36 hours. If your original right hand value for stitching labor was 30 hours, you know that:
A) the next worker that offers to work an extra 8 hours should receive at least $80.
B) you can send someone home 6 hours early and still pay them the $60 they would have earned while on the clock.
C) you would be willing pay up to $60 for someone to work another 6 hours.
D) you would lose $80 if one of your workers missed an entire 8 hour shift.
A) the next worker that offers to work an extra 8 hours should receive at least $80.
B) you can send someone home 6 hours early and still pay them the $60 they would have earned while on the clock.
C) you would be willing pay up to $60 for someone to work another 6 hours.
D) you would lose $80 if one of your workers missed an entire 8 hour shift.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
55
A(n) ________ is the marginal improvement in the objective function value caused by relaxing a constraint by one unit.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
56
The interval over which the right-hand-side parameter of a constraint can vary while its shadow price remains valid is the ________.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
57
In a linear programming model formulation, what is the meaning of a slack or surplus variable?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
58
For an "equal" constraint, only points ________ are feasible solutions.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
59
A(n) ________ limits the ability to improve the objective function.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
60
What are the limitations of the graphical method of linear programming?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
61
Degeneracy occurs when the linear program model consists of only an infeasible region.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
62
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.
Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the total output be for month 3?
A) between 350 and 400 units
B) between 400 and 450 units
C) between 450 and 500 units
D) more than 500 units
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the total output be for month 3?
A) between 350 and 400 units
B) between 400 and 450 units
C) between 450 and 500 units
D) more than 500 units

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
63
Table D.3
The Harper Company is in the process of production planning for the next four quarters. The company follows a policy of a stable workforce and uses overtime and subcontracting to meet uneven forecasted demand. Anticipation inventory is also allowed, but not backorders. Undertime is paid, at a rate of $5.00 per unit. The beginning (or current) inventory is 25 units. Details are shown in the following POM for Windows table.
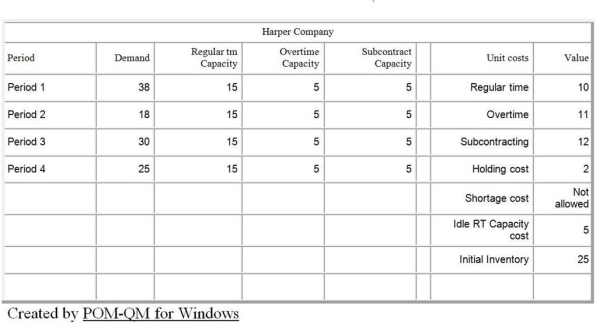
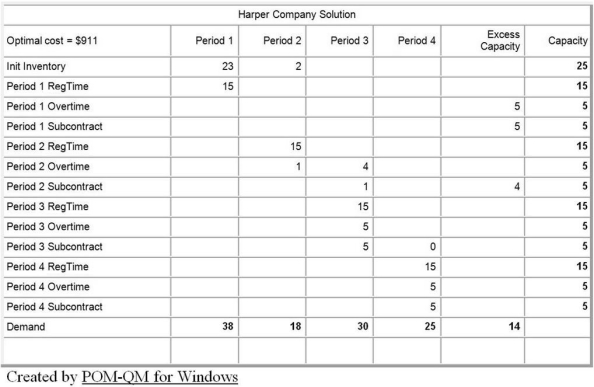
Use the information in Table D.3. What is the anticipation inventory at the end of the first quarter?
A) 0 units
B) 1 through 5 units
C) 6 through 10 units
D) 11 units and above
The Harper Company is in the process of production planning for the next four quarters. The company follows a policy of a stable workforce and uses overtime and subcontracting to meet uneven forecasted demand. Anticipation inventory is also allowed, but not backorders. Undertime is paid, at a rate of $5.00 per unit. The beginning (or current) inventory is 25 units. Details are shown in the following POM for Windows table.


Use the information in Table D.3. What is the anticipation inventory at the end of the first quarter?
A) 0 units
B) 1 through 5 units
C) 6 through 10 units
D) 11 units and above

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
64
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a chase plan strategy for the six-month planning period. What is the cost for month 6 of their chase plan?
A) $8,000
B) $9,852
C) $11,317
D) $12,631
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a chase plan strategy for the six-month planning period. What is the cost for month 6 of their chase plan?
A) $8,000
B) $9,852
C) $11,317
D) $12,631

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
65
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the regular output be for month 3?
A) between 290 and 330 units
B) between 330 and 370 units
C) between 370 and 410 units
D) between 410 and 450 units
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the regular output be for month 3?
A) between 290 and 330 units
B) between 330 and 370 units
C) between 370 and 410 units
D) between 410 and 450 units

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
66
What is degeneracy in the context of linear programming? Why is degeneracy a concern?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
67
A small oil company has a refining budget of $200,000 and would like to determine the optimal production plan for profitability. The following table lists the costs associated with its three products.
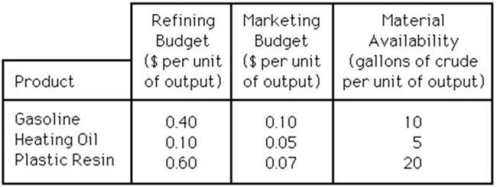
Marketing has a budget of $50,000, and the company has 750,000 gallons of crude oil available. Each gallon of gasoline contributes 14 cents of profits, heating oil provides 10 cents, and plastic resin 30 cents per unit. The refining process results in a ratio of two units of heating oil for each unit of gasoline produced. This problem has been modeled as a linear programming problem and solved on the computer. The set up and output follows:
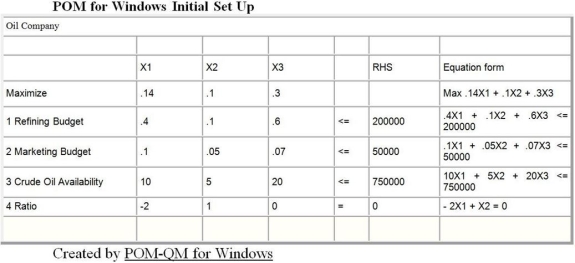
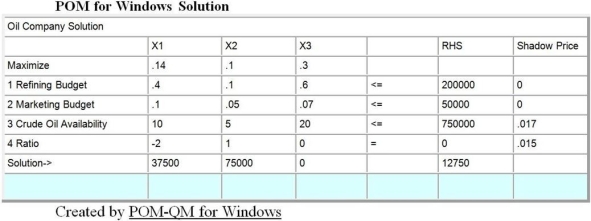
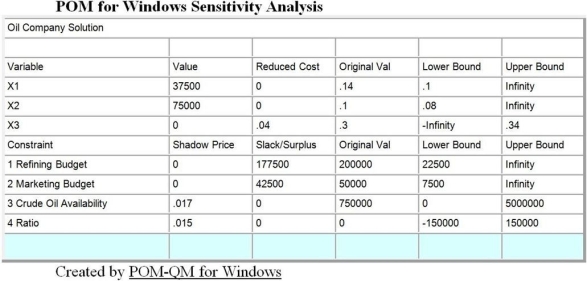
a. Give a linear programming formulation for this problem. Make the variable definitions and constraints line up with the computer output.
b. What product mix maximizes the profit for the company using its limited resources?
c. How much plastic resin is produced if profits are maximized?
d. Give a full explanation of the meaning of the three numbers listed following.
First Number: Slack or surplus of 42,500 for the #2 Marketing Budget constraint.
Second Number: Shadow price of 0 for the #1 Refining Budget constraint.
Third Number: An upper limit of "infinity" for the right-hand-side value for the #1 Refining Budget constraint.

Marketing has a budget of $50,000, and the company has 750,000 gallons of crude oil available. Each gallon of gasoline contributes 14 cents of profits, heating oil provides 10 cents, and plastic resin 30 cents per unit. The refining process results in a ratio of two units of heating oil for each unit of gasoline produced. This problem has been modeled as a linear programming problem and solved on the computer. The set up and output follows:



a. Give a linear programming formulation for this problem. Make the variable definitions and constraints line up with the computer output.
b. What product mix maximizes the profit for the company using its limited resources?
c. How much plastic resin is produced if profits are maximized?
d. Give a full explanation of the meaning of the three numbers listed following.
First Number: Slack or surplus of 42,500 for the #2 Marketing Budget constraint.
Second Number: Shadow price of 0 for the #1 Refining Budget constraint.
Third Number: An upper limit of "infinity" for the right-hand-side value for the #1 Refining Budget constraint.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
68
D.5 The Transportation Method
Table D.1
Tanfastic, Inc., a manufacturer of swimwear, is in the process of developing a production plan for the coming spring break. The ending inventory for January is 30 units. Undertime is paid, at a rate of $5.00 per unit. Details are shown in the following POM for Windows table.
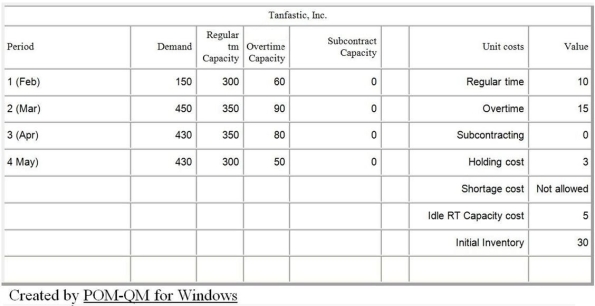
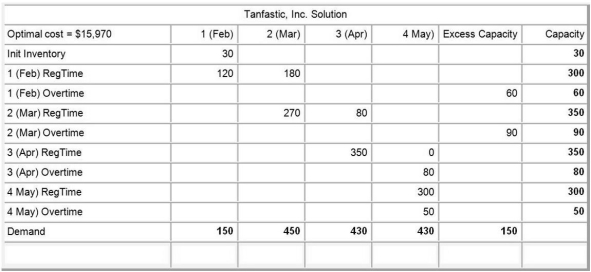
Use the information in Table D.1. Given the information in the optimal tableau, what is the overtime cost in dollars per unit?
A) less than $12
B) greater than $12 but less than or equal to $14
C) greater than $14 but less than or equal to $16
D) greater than $16
Table D.1
Tanfastic, Inc., a manufacturer of swimwear, is in the process of developing a production plan for the coming spring break. The ending inventory for January is 30 units. Undertime is paid, at a rate of $5.00 per unit. Details are shown in the following POM for Windows table.



Use the information in Table D.1. Given the information in the optimal tableau, what is the overtime cost in dollars per unit?
A) less than $12
B) greater than $12 but less than or equal to $14
C) greater than $14 but less than or equal to $16
D) greater than $16

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
69
The CZ Jewelry Company produces two products: (1) engagement rings and (2) jeweled watches. The production process for each is similar in that both require a certain number of hours of diamond work and a certain number of labor hours in the gold department. Each ring takes four hours of diamond work and two hours in the gold shop. Each watch requires three hours in diamonds and one hour in the gold department. There are 240 hours of diamond labor available and 100 hours of gold department time available for the next month. Each engagement ring sold yields a profit of $9; each watch produced may be sold for a $10 profit.
a. Give a complete formulation of this problem, including a careful definition of your decision variables. Let the first decision variable, (X₁), deal with rings, the second decision variable, (X₂), with watches, the first constraint with diamonds, and the second constraint with gold.
b. Graph the problem fully in the following space. Label the axes carefully, plot the constraints, shade the feasibility region, plot at least one isoprofit line that reveals the optimal solution, circle the corner points and highlight the optimal corner point so found, and solve for it algebraically. (Show all your work to get credit.)
a. Give a complete formulation of this problem, including a careful definition of your decision variables. Let the first decision variable, (X₁), deal with rings, the second decision variable, (X₂), with watches, the first constraint with diamonds, and the second constraint with gold.
b. Graph the problem fully in the following space. Label the axes carefully, plot the constraints, shade the feasibility region, plot at least one isoprofit line that reveals the optimal solution, circle the corner points and highlight the optimal corner point so found, and solve for it algebraically. (Show all your work to get credit.)


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
70
A very confused manager is reading a two-page report given to him by his student intern. "She told me that she had my problem solved, gave me this, and then said she was off to her production management course," he whined. "I gave her my best estimates of my on-hand inventories and requirements to produce, but what if my numbers are slightly off? I recognize the names of our four models W, X, Y, and Z, but that's about it. Can you figure out what I'm supposed to do and why?" You take the report from his hands and note that it is the answer report and the sensitivity report from Excel's solver routine.
Explain each of the highlighted cells in layman's terms and tell the manager what they mean in relation to his problem.
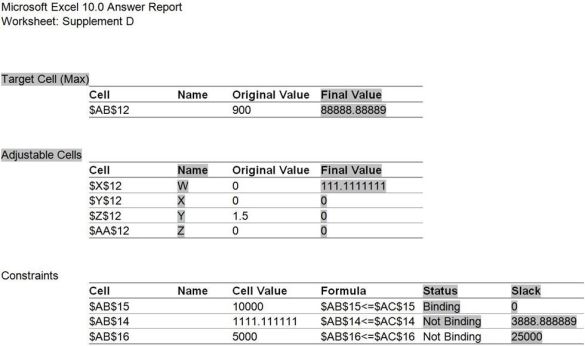
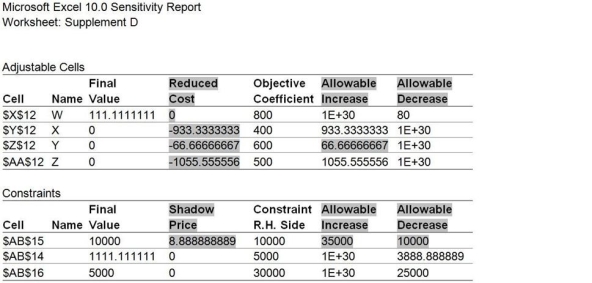
Explain each of the highlighted cells in layman's terms and tell the manager what they mean in relation to his problem.



Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
71
Table D.3
The Harper Company is in the process of production planning for the next four quarters. The company follows a policy of a stable workforce and uses overtime and subcontracting to meet uneven forecasted demand. Anticipation inventory is also allowed, but not backorders. Undertime is paid, at a rate of $5.00 per unit. The beginning (or current) inventory is 25 units. Details are shown in the following POM for Windows table.


Use the information in Table D.3. What is the total cost of the optimal production plan?
A) less than or equal to $1,000
B) greater than $1,000 but less than or equal to $2,000
C) greater than $2,000 but less than or equal to $3,000
D) greater than $3,000
The Harper Company is in the process of production planning for the next four quarters. The company follows a policy of a stable workforce and uses overtime and subcontracting to meet uneven forecasted demand. Anticipation inventory is also allowed, but not backorders. Undertime is paid, at a rate of $5.00 per unit. The beginning (or current) inventory is 25 units. Details are shown in the following POM for Windows table.


Use the information in Table D.3. What is the total cost of the optimal production plan?
A) less than or equal to $1,000
B) greater than $1,000 but less than or equal to $2,000
C) greater than $2,000 but less than or equal to $3,000
D) greater than $3,000

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
72
The simplex method deals exclusively with corner points

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
73
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a level plan strategy for the six-month planning period. What is the cost for month 6 of their level plan?
A) between $16,200 and $16,600
B) between $16,600 and $17,000
C) between $17,000 and $17,400
D) between $17,400 and $17,800
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a level plan strategy for the six-month planning period. What is the cost for month 6 of their level plan?
A) between $16,200 and $16,600
B) between $16,600 and $17,000
C) between $17,000 and $17,400
D) between $17,400 and $17,800

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
74
________ occurs in a linear programming problem when the number of nonzero variables in the optimal solution is fewer than the number of constraints.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
75
The simplex method is an interactive algebraic procedure for solving linear programming problems.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
76
D.5 The Transportation Method
Table D.1
Tanfastic, Inc., a manufacturer of swimwear, is in the process of developing a production plan for the coming spring break. The ending inventory for January is 30 units. Undertime is paid, at a rate of $5.00 per unit. Details are shown in the following POM for Windows table.



Use the information in Table D.1. Given the information in the optimal tableau, what is the inventory carrying cost, in dollars per unit per quarter?
A) less than $1
B) greater than $1 but less than or equal to $2
C) greater than $2 but less than or equal to $3
D) greater than $3
Table D.1
Tanfastic, Inc., a manufacturer of swimwear, is in the process of developing a production plan for the coming spring break. The ending inventory for January is 30 units. Undertime is paid, at a rate of $5.00 per unit. Details are shown in the following POM for Windows table.



Use the information in Table D.1. Given the information in the optimal tableau, what is the inventory carrying cost, in dollars per unit per quarter?
A) less than $1
B) greater than $1 but less than or equal to $2
C) greater than $2 but less than or equal to $3
D) greater than $3

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
77
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the plant has no limits on the number of units produced by overtime or subcontractors, what is the lowest-cost chase plan that is possible for the six-month period?
A) less than $50,000
B) between $50,000 and $100,000
C) between $100,000 and $150,000
D) between $150,000 and $200,000
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the plant has no limits on the number of units produced by overtime or subcontractors, what is the lowest-cost chase plan that is possible for the six-month period?
A) less than $50,000
B) between $50,000 and $100,000
C) between $100,000 and $150,000
D) between $150,000 and $200,000

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
78
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four-ounce portion must contain 22 units of protein, 15 units of vitamin A, and 8 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 6 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 8 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 8 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 5 cents per ounce, and eggs cost 12 cents per ounce. To make the production process as easy as possible, she would like to make exactly four ounces of cat food from her recipe. She used POM for Windows and received the following results. Provide an interpretation.
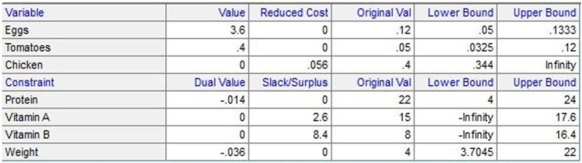


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
79
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the planner decides to adopt a chase plan for the planning period, what will the regular output be for month 1?
A) 300 units
B) 350 units
C) 400 units
D) 450 units
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.

Use the information in Table D.2. If the planner decides to adopt a chase plan for the planning period, what will the regular output be for month 1?
A) 300 units
B) 350 units
C) 400 units
D) 450 units

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
80
The Really Big Shoe Company is a manufacturer of basketball shoes and football shoes. Ed Sullivan, the manager of marketing, must decide the best way to spend advertising resources. Each football team sponsored requires 120 pairs of shoes. Each basketball team requires 32 pairs of shoes. Football coaches receive $300,000 for shoe sponsorship and basketball coaches receive $1,000,000. Ed's promotional budget is $30,000,000. The Really Big Shoe Company has a very limited supply (4 liters or 4,000cc) of flubber, a rare and costly raw material used only in promotional athletic shoes. Each pair of basketball shoes requires 3cc of flubber, and each pair of football shoes requires 1cc of flubber. Ed desires to sponsor as many basketball and football teams as resources allow. However, he has already committed to sponsoring 19 football teams and wants to keep his promises.
a. Give a linear programming formulation for Ed. Make the variable definitions and constraints line up with the computer output appended to this exam.
b. Solve the problem graphically, showing constraints, feasible region, and isoprofit lines. Circle the optimal solution, making sure that the isoprofit lines drawn make clear why you chose this point. (Show all your calculations for plotting the constraints and isoprofit line on the left to get credit.)
c. Solve algebraically for the corner point on the feasible region.
d. Part of Ed's computer output is shown following. Give a full explanation of the meaning of the three numbers listed below. Based on your graphical and algebraic analysis, explain why these numbers make sense. (Hint: He formulated the budget constraint in terms of $000.) See the computer printout that follows.
First Number: The shadow price of 0.0104 for the "Flubber" constraint.
Second Number: The slack or surplus of 6383.334 for the "Budget" constraint.
Third Number: The lower limit of 12.2807 for the "Commitment" constraint.
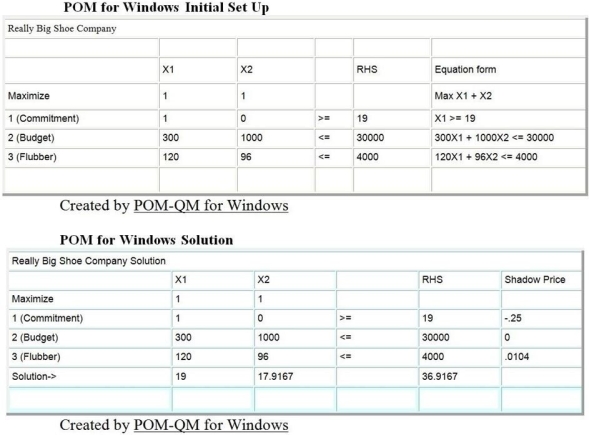
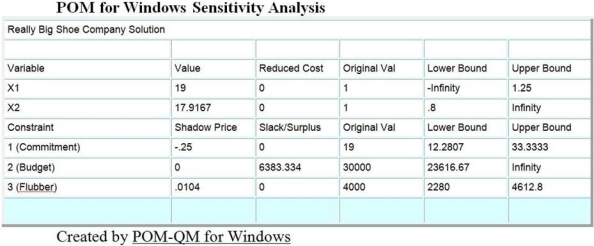
a. Give a linear programming formulation for Ed. Make the variable definitions and constraints line up with the computer output appended to this exam.
b. Solve the problem graphically, showing constraints, feasible region, and isoprofit lines. Circle the optimal solution, making sure that the isoprofit lines drawn make clear why you chose this point. (Show all your calculations for plotting the constraints and isoprofit line on the left to get credit.)

c. Solve algebraically for the corner point on the feasible region.
d. Part of Ed's computer output is shown following. Give a full explanation of the meaning of the three numbers listed below. Based on your graphical and algebraic analysis, explain why these numbers make sense. (Hint: He formulated the budget constraint in terms of $000.) See the computer printout that follows.
First Number: The shadow price of 0.0104 for the "Flubber" constraint.
Second Number: The slack or surplus of 6383.334 for the "Budget" constraint.
Third Number: The lower limit of 12.2807 for the "Commitment" constraint.



Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck


