Deck 2: Line and Angle Relationships
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/35
Play
Full screen (f)
Deck 2: Line and Angle Relationships
1
According to the Angle-Addition Postulate, m 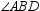
 m
m 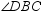 = m
= m 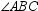 .
.
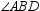
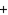 m
m 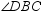 = m
= m 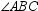 .
.False
2
Name the property that justifies the following conclusion:
If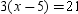 , then
, then 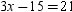 .
.
If
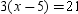 , then
, then 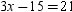 .
.NOT ANSWERED.
3
Given that  and
and 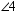 are complementary, what conclusion may you draw?
are complementary, what conclusion may you draw?
 and
and 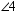 are complementary, what conclusion may you draw?
are complementary, what conclusion may you draw?NOT ANSWERED.
4
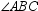 can also be called
can also be called 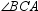 .
.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
5
The relation between lines, "is perpendicular to," has a transitive property.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
6
Where x is the measure of an angle and 0° x 90°, the angle is an obtuse angle.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
7
Points A, B, and C are said to be collinear if they lie on a line.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
8
An angle is the union of two rays that have a common endpoint.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
9
In geometry, what is a postulate?
A)statement that defines a term
B)statement that must be proved
C)a type of geometric figure
D)None of These
A)statement that defines a term
B)statement that must be proved
C)a type of geometric figure
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
10
In this figure, 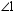 and
and  are complementary. Also,
are complementary. Also,  and
and  are complementary. Regarding
are complementary. Regarding 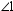 and
and  , what conclusion may you draw?
, what conclusion may you draw?
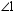 and
and  are complementary. Also,
are complementary. Also,  and
and  are complementary. Regarding
are complementary. Regarding 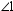 and
and  , what conclusion may you draw?
, what conclusion may you draw?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
11
If m 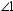 = x and 90 ° x 180 ° , then
= x and 90 ° x 180 ° , then 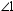 is a(n):
is a(n):
A)acute angle
B)right angle
C)obtuse angle
D)straight angle
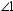 = x and 90 ° x 180 ° , then
= x and 90 ° x 180 ° , then 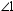 is a(n):
is a(n):A)acute angle
B)right angle
C)obtuse angle
D)straight angle

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
12
Considering the definitions and postulates of geometry, which of the following is a correct statement?
A)An angle has more than one angle-bisector.
B)A line segment has two midpoints.
C)A line segment has two endpoints.
D)A plane contains exactly three noncollinear points.
A)An angle has more than one angle-bisector.
B)A line segment has two midpoints.
C)A line segment has two endpoints.
D)A plane contains exactly three noncollinear points.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
13
For a construction problem, which instrument could you use?
A)calculator
B)protractor
C)tape measure
D)compass
A)calculator
B)protractor
C)tape measure
D)compass

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the definition: An isosceles triangle is a triangle that has two congruent sides. Which result must follow from the definition?
A)If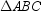 is isosceles, then it has two congruent angles.
is isosceles, then it has two congruent angles.
B)If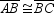 in
in 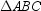 , then
, then 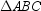 is an isosceles triangle.
is an isosceles triangle.
C)If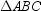 has two congruent sides, then
has two congruent sides, then 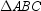 has two congruent angles.
has two congruent angles.
D)None of These
A)If
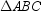 is isosceles, then it has two congruent angles.
is isosceles, then it has two congruent angles.B)If
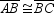 in
in 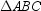 , then
, then 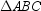 is an isosceles triangle.
is an isosceles triangle.C)If
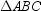 has two congruent sides, then
has two congruent sides, then 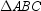 has two congruent angles.
has two congruent angles.D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
15
A postulate is accepted without proof while a theorem is a statement that must be proved.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
16
In the figure,  and
and 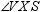 are known as vertical angles.
are known as vertical angles.
 and
and 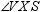 are known as vertical angles.
are known as vertical angles.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
17
Which property justifies this conclusion? If X is a point on 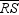 and R - X - S , then
and R - X - S , then 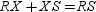 .
.
A)Segment-Addition Postulate
B)Line-Addition Postulate
C)Ruler Postulate
D)None of These
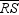 and R - X - S , then
and R - X - S , then 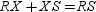 .
.A)Segment-Addition Postulate
B)Line-Addition Postulate
C)Ruler Postulate
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
18
Points A , B , and C are collinear on horizontal line segment 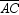 . Point D lies above
. Point D lies above 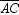 . If m
. If m 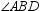 is 14 ° larger than m
is 14 ° larger than m 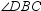 , find m
, find m 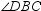 .
.
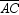 . Point D lies above
. Point D lies above 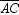 . If m
. If m 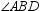 is 14 ° larger than m
is 14 ° larger than m 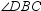 , find m
, find m 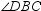 .
.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
19
Consider a set of lines. Which is a property of the relation "is perpendicular to" for lines?
A)Reflexive
B)Symmetric
C)Transitive
D)None of These
A)Reflexive
B)Symmetric
C)Transitive
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
20
Which is not a method of reasoning used in geometry?
A)construction
B)induction
C)intuition
D)deduction
A)construction
B)induction
C)intuition
D)deduction

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
21
Given that 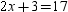 , which operation leads to the conclusion that
, which operation leads to the conclusion that 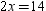 ?
?
A)adding 3 to each side of the equation
B)adding -3 to each side of the equation
C)subtracting -3 from each side of the equation
D)None of These
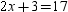 , which operation leads to the conclusion that
, which operation leads to the conclusion that 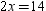 ?
?A)adding 3 to each side of the equation
B)adding -3 to each side of the equation
C)subtracting -3 from each side of the equation
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
22
If 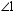 and
and  are complementary, then each of these angles 1 and 2 is acute.
are complementary, then each of these angles 1 and 2 is acute.
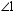 and
and  are complementary, then each of these angles 1 and 2 is acute.
are complementary, then each of these angles 1 and 2 is acute.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
23
With 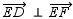 and point G in the interior of
and point G in the interior of 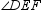 ,
, 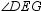 and
and 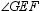 are complementary.
are complementary.
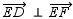 and point G in the interior of
and point G in the interior of 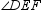 ,
, 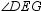 and
and 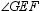 are complementary.
are complementary.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
24
If 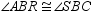 , then it can be proved that:
, then it can be proved that:
A)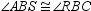
B)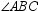 is a right angle
is a right angle
C)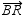 bisects
bisects 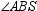
D)None of These
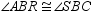 , then it can be proved that:
, then it can be proved that:A)
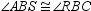
B)
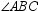 is a right angle
is a right angleC)
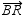 bisects
bisects 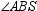
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
25
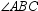 and
and 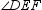 are supplementary.
are supplementary. 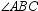 is acute. What type of angle is
is acute. What type of angle is 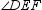 ?
?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
26
When using induction, one draws a conclusion based upon numerous examples or test results.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
27
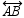 and
and 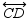 intersect at point E . If
intersect at point E . If 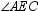 is a right angle, what relationship exists between
is a right angle, what relationship exists between 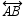 and
and 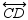 ?
?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
28
Given A - B - C and m 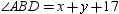 while m
while m 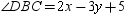 , it follows that:
, it follows that:
A)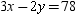
B)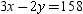
C)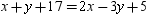
D)None of These
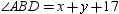 while m
while m 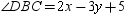 , it follows that:
, it follows that:A)
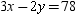
B)
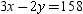
C)
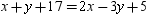
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
29
The exterior sides of adjacent angles 1 and 2 are perpendicular. If 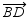 is the bisector of
is the bisector of 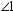 and
and 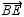 is the bisector of
is the bisector of  , find the measure of
, find the measure of 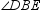 .
.
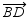 is the bisector of
is the bisector of 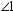 and
and 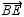 is the bisector of
is the bisector of  , find the measure of
, find the measure of 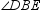 .
.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
30
Because it has rained the past 4 days, a person's intuition can be used to conclude that it will definitely rain again tomorrow.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
31
If two rays are opposite rays, then their union is a straight line.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the noncollinear points A, B, C, and D. By using two points at a time, find the total number of lines that they determine.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
33
If M is the midpoint of 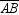 , then it can be proved that:
, then it can be proved that:
A)N is also the midpoint of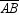 .
.
B)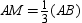
C)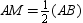
D)None of These
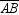 , then it can be proved that:
, then it can be proved that:A)N is also the midpoint of
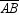 .
.B)
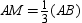
C)
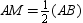
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
34
If ray BD bisects 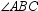 , then
, then 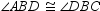 .
.
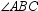 , then
, then 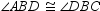 .
.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
35
Given that 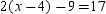 , you can prove that:
, you can prove that:
A)x = 2
B)x = 15
C)x = 16
D)None of These
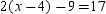 , you can prove that:
, you can prove that:A)x = 2
B)x = 15
C)x = 16
D)None of These

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck


