Deck 15: Systems of Equations: Matrices and Determinants
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/228
Play
Full screen (f)
Deck 15: Systems of Equations: Matrices and Determinants
1
The elimination-by-addition method and the graphing method can be used to obtain exact solutions for any system of two linear equations in two unknowns.
False
2
Solve the problem by using a system of equations. The tens digit of a two-digit number is 7 less than three times the units digit. If the sum of the digits is 9, find the number.
A) 57
B) 54
C) 45
D) 48
A) 57
B) 54
C) 45
D) 48
54
3
An inconsistent system has exactly one solution.
False
4
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate.
A) (600, 1,800)
B) (400, 1,200)
C) dependent
D) inconsistent
A) (600, 1,800)
B) (400, 1,200)
C) dependent
D) inconsistent

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
6
Michelle can enter a small business as a full partner and receive a salary of $40,000 a year and 15% of the year's profit, or she can be sales manager for a salary of $75,000 plus 5% of the year's profit. What must the year's profit be for her total earnings to be the same whether she is a full partner or a sales manager?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem by using a system of equations. The sum of the digits of a two-digit number is 17. If the digits are reversed, the newly formed number is 9 larger than the original number. Find the original number.
A) 90
B) 98
C) 99
D) 89
A) 90
B) 98
C) 99
D) 89

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the problem by using a system of equations. The tens digit of a two-digit number is 17 less than three times the units digit. If the sum of the digits is 11, find the number.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system by using the elimination-by-addition method. 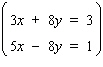 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
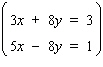 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the problem by using a system of equations. The sum of the digits of a two-digit number is 7. If the digits are reversed, the newly formed number is 45 larger than the original number. Find the original number.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by using the substitution method. 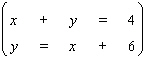 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
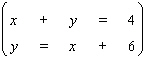 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
12
A video store rents new release movies for $5 and favorites for $2.55. One day the number of new release movies rented was twice the number of favorites. If the total income for that day was $815.75, how many movies of each kind were rented?
A) 140 new release, 70 favorites
B) 150 new release, 75 favorites
C) 70 new release, 140 favorites
D) 65 new release, 130 favorites
E) 130 new release, 65 favorites
A) 140 new release, 70 favorites
B) 150 new release, 75 favorites
C) 70 new release, 140 favorites
D) 65 new release, 130 favorites
E) 130 new release, 65 favorites

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
13
Michelle can enter a small business as a full partner and receive a salary of $40,000 a year and 10% of the year's profit, or she can be sales manager for a salary of $75,000 plus 5% of the year's profit. What must the year's profit be for her total earnings to be the same whether she is a full partner or a sales manager? Year's profit = $__________

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system by using the elimination-by-addition method.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
15
One day last summer, Jim went kayaking on the Little Susitna River in Alaska. Paddling upstream against the current, he traveled 12 miles in 3 hours. Then he turned around and paddled twice as fast downstream and, with the help of the current, traveled 17 miles in 1 hour. Find the rate of the current. __________ miles per hour

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the system by using substitution. 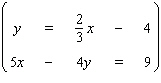 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
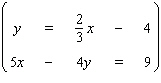 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
17
One day last summer, Jim went kayaking on the Little Susitna River in Alaska. Paddling upstream against the current, he traveled 24 miles in 3 hours. Then he turned around and paddled twice as fast downstream and, with the help of the current, traveled 25 miles in 1 hour. Find the rate of the current.
A) 14 mph
B) 8 mph
C) 11 mph
D) 3 mph
A) 14 mph
B) 8 mph
C) 11 mph
D) 3 mph

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
18
When the graphs for a system of two linear equations are parallel lines, then there is no solution.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system by using substitution. 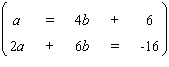 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( a , b ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( a , b ).
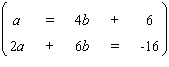 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( a , b ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( a , b ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
20
A system of two linear equations can be solved by graphing the lines on the same set of axes.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the system.
A) x = 2, y = 5, z = -2
B) x = 3, y = 5, z = -3
C) x = 3, y = 4, z = -2
D) x = 2, y = 6, z = -3
A) x = 2, y = 5, z = -2
B) x = 3, y = 5, z = -3
C) x = 3, y = 4, z = -2
D) x = 2, y = 6, z = -3

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
22
A video store rents new release movies for $5 and favorites for $2.65. One day the number of new release movies rented was twice the number of favorites. If the total income for that day was $822.25, how many movies of each kind were rented? __________ new release __________ favorites

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the system.
A) x = 6, y = -2, z = 0
B) x = 5, y = 1, z = 0
C) x = 4, y = -1, z = 3
D) x = 6, y = -4, z = 3
A) x = 6, y = -2, z = 0
B) x = 5, y = 1, z = 0
C) x = 4, y = -1, z = 3
D) x = 6, y = -4, z = 3

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the system.
A) x = -2, y = 1, z = 4
B) x = -3, y = 3, z = 7
C) x = 1, y = 0, z = 7
D) x = -3, y = 4, z = 4
A) x = -2, y = 1, z = 4
B) x = -3, y = 3, z = 7
C) x = 1, y = 0, z = 7
D) x = -3, y = 4, z = 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system.
A) x = 4, y = 2, z = 5
B) x = 5, y = 1, z = 3
C) x = 3, y = -1, z = 3
D) x = 3, y = 0, z = 5
A) x = 4, y = 2, z = 5
B) x = 5, y = 1, z = 3
C) x = 3, y = -1, z = 3
D) x = 3, y = 0, z = 5

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the system.
A) x = -4, y = 4, z = 2
B) x = -2, y = 0, z = 6
C) x = 1, y = 3, z = 2
D) x = -2, y = 1, z = 3
A) x = -4, y = 4, z = 2
B) x = -2, y = 0, z = 6
C) x = 1, y = 3, z = 2
D) x = -2, y = 1, z = 3

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
27
A system of three linear equations in three variables produces three intersecting planes when graphed.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 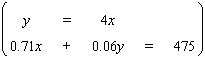 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
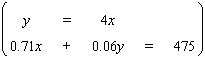 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 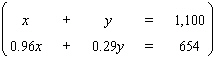 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
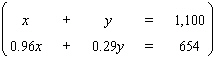 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
30
In a system of three linear equations, if two of the planes coincide the solution is infinitely many solutions.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 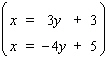 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
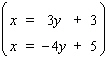 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 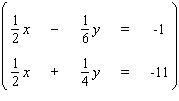 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
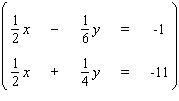 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 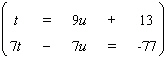 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( t , u ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( t , u ).
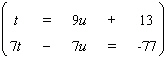 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( t , u ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( t , u ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the system by using the elimination-by-addition method. 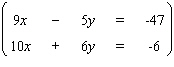 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
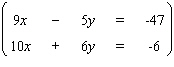 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the system by using the elimination-by-addition method. 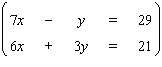 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
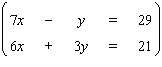 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
36
To solve the system , solve the equation first.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
37
The solution set is infinitely many ordered triples if the three planes have a common line of intersection..

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 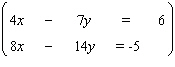 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
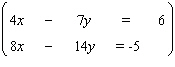 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate. 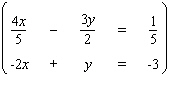 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ), enter x and y as fractions.
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ), enter x and y as fractions.
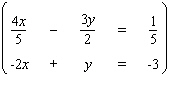 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ), enter x and y as fractions.
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ), enter x and y as fractions.
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the system by using the elimination-by- addition method. 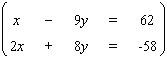 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
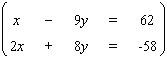 If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
If the equations of the system are dependent, or if a system is inconsistent, so indicate. In those cases enter dependent or inconsistent . Otherwise, enter your answer as an ordered pair ( x , y ).
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the system.
A) x = 2, y = -5, z = 2
B) x = 3, y = -3, z = 5
C) x = 2, y = -6, z = 4
D) x = 4, y = -5, z = 4
A) x = 2, y = -5, z = 2
B) x = 3, y = -3, z = 5
C) x = 2, y = -6, z = 4
D) x = 4, y = -5, z = 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the system. 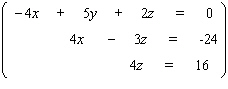
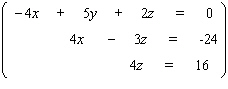

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
43
A gift store is making a mixture of almonds, pecans, and peanuts, which sell for $3.50 per pound, $5.00 per pound, and $1.00 per pound, respectively. The storekeeper wants to make 15 pounds of the mix to sell at $2.30 per pound. The number of pounds of peanuts is to be three times the number of pounds of pecans. Find the number of pounds of each to be used in the mixture.
A) 6 pounds of almonds, 6 pounds of pecans, and 8 pounds of peanuts
B) 9 pounds of almonds, 2 pounds of pecans, and 9 pounds of peanuts
C) 6 pounds of almonds, 6 pounds of pecans, and 12 pounds of peanuts
D) 3 pounds of almonds, 3 pounds of pecans, and 9 pounds of peanuts
A) 6 pounds of almonds, 6 pounds of pecans, and 8 pounds of peanuts
B) 9 pounds of almonds, 2 pounds of pecans, and 9 pounds of peanuts
C) 6 pounds of almonds, 6 pounds of pecans, and 12 pounds of peanuts
D) 3 pounds of almonds, 3 pounds of pecans, and 9 pounds of peanuts

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the system.
A) x = 2, y = 0, z = -7
B) x = 2, y = -2, z = -7
C) x = -1, y = -3, z = -5
D) x = -1, y = -5, z = -2
A) x = 2, y = 0, z = -7
B) x = 2, y = -2, z = -7
C) x = -1, y = -3, z = -5
D) x = -1, y = -5, z = -2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the system. 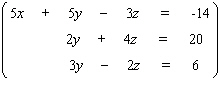
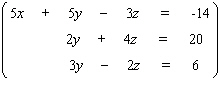

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the system. 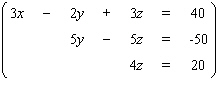
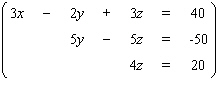

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system. 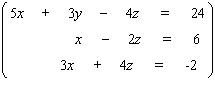
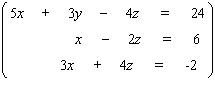

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
48
A small company makes three different types of bird houses. Each type requires the services of three different departments, as indicated by the following table. Type A Type B Type C Cutting department 0.2 hour 0.1 hour 0.3 hour Finishing department 0.5 hour 0.5 hour 0.4 hour Assembly department 0.1 hour 0.1 hour 0.3 hour The cutting, finishing, and assembly departments have available a maximum of 61, 128, and 52 work-hours per week, respectively. How many bird houses of each type should be made per week so that the company is operating at full capacity?
A) 70 houses of type A, 60 houses of type B, and 100 houses of type C
B) 90 houses of type A, 70 houses of type B, and 120 houses of type C
C) 80 houses of type A, 60 houses of type B, and 100 houses of type C
D) 90 houses of type A, 60 houses of type B, and 110 houses of type C
A) 70 houses of type A, 60 houses of type B, and 100 houses of type C
B) 90 houses of type A, 70 houses of type B, and 120 houses of type C
C) 80 houses of type A, 60 houses of type B, and 100 houses of type C
D) 90 houses of type A, 60 houses of type B, and 110 houses of type C

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the system.
A) x = 4, y = 5, z = -1
B) x = 2, y = 4, z = -1
C) x = -1, y = 8, z = 0
D) x = -1, y = 2, z = -2
A) x = 4, y = 5, z = -1
B) x = 2, y = 4, z = -1
C) x = -1, y = 8, z = 0
D) x = -1, y = 2, z = -2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the system. 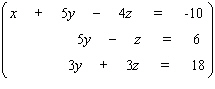
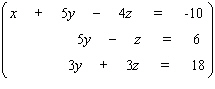

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the system.
A) x = 0, y = -5, z = 1
B) x = 4, y = -3, z = 2
C) x = 3, y = -6, z = 4
D) x = 0, y = -4, z = 4
A) x = 0, y = -5, z = 1
B) x = 4, y = -3, z = 2
C) x = 3, y = -6, z = 4
D) x = 0, y = -4, z = 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system.
A) x = 5, y = -3, z = 2
B) x = 3, y = -1, z = 5
C) x = 5, y = 0, z = 4
D) x = 5, y = 2, z = 5
A) x = 5, y = -3, z = 2
B) x = 3, y = -1, z = 5
C) x = 5, y = 0, z = 4
D) x = 5, y = 2, z = 5

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
53
Part of $10,000 is invested at 9%, another part at 11%, and the remainder at 12% yearly interest. The total yearly income from the three investments is $1,100. The sum of the amounts invested at 9% and 11% equals the amount invested at 12%. How much is invested at each rate?
A) $2,500 at 9%, $2,500 at 11%, and $5,000 at 12%
B) $1,500 at 9%, $2,500 at 11%, and $6,000 at 12%
C) $1,500 at 9%, $2,000 at 11%, and $6,000 at 12%
D) $3,000 at 9%, $2,000 at 11%, and $5,000 at 12%
A) $2,500 at 9%, $2,500 at 11%, and $5,000 at 12%
B) $1,500 at 9%, $2,500 at 11%, and $6,000 at 12%
C) $1,500 at 9%, $2,000 at 11%, and $6,000 at 12%
D) $3,000 at 9%, $2,000 at 11%, and $5,000 at 12%

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the system.
A) , is a real number
B) , is a real number
C) , is a real number
D) , is a real number
E) , is a real number
A) , is a real number
B) , is a real number
C) , is a real number
D) , is a real number
E) , is a real number

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the system.
A) x = 5, y = -2, z = 2
B) x = 7, y = -4, z = 2
C) x = 2, y = -1, z = 6
D) x = 2, y = -4, z = 4
A) x = 5, y = -2, z = 2
B) x = 7, y = -4, z = 2
C) x = 2, y = -1, z = 6
D) x = 2, y = -4, z = 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the system.
A) x = 3, y = -2, z = -6
B) x = -1, y = 1, z = -6
C) x = 1, y = -4, z = -4
D) x = 1, y = -1, z = -3
A) x = 3, y = -2, z = -6
B) x = -1, y = 1, z = -6
C) x = 1, y = -4, z = -4
D) x = 1, y = -1, z = -3

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
57
A box contains $6.80 in nickels, dimes, and quarters. There are 40 coins in all, and the sum of the numbers of nickels and dimes is two less than the number of quarters. How many coins of each kind are there?
A) 7 nickels, 12 dimes, and 21 quarters
B) 11 nickels, 11 dimes, and 18 quarters
C) 6 nickels, 13 dimes, and 21 quarters
D) 6 nickels, 10 dimes, and 25 quarters
A) 7 nickels, 12 dimes, and 21 quarters
B) 11 nickels, 11 dimes, and 18 quarters
C) 6 nickels, 13 dimes, and 21 quarters
D) 6 nickels, 10 dimes, and 25 quarters

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
58
The measure of the largest angle of a triangle is twice the measure of the smallest angle. The sum of the smallest angle and the largest angle is twice the other angle. Find the measure of each angle.
A) 55o, 60o, 65o
B) 45o, 60o, 75o
C) 30o, 60o, 90o
D) 40o, 60o, 80o
A) 55o, 60o, 65o
B) 45o, 60o, 75o
C) 30o, 60o, 90o
D) 40o, 60o, 80o

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the system.
A) x = -1, y = -6, z = 2
B) x = -1, y = -7, z = 2
C) x = -4, y = -3, z = -1
D) x = 2, y = -4, z = 1
A) x = -1, y = -6, z = 2
B) x = -1, y = -7, z = 2
C) x = -4, y = -3, z = -1
D) x = 2, y = -4, z = 1

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the system.
A) x = 1, y = -6, z = 3
B) x = 0, y = -4, z = 1
C) x = 0, y = -7, z = 1
D) x = 1, y = -3, z = 4
A) x = 1, y = -6, z = 3
B) x = 0, y = -4, z = 1
C) x = 0, y = -7, z = 1
D) x = 1, y = -3, z = 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
61
The measure of the largest angle of a triangle is twice the measure of the smallest angle. The sum of the smallest angle and the largest angle is twice the other angle. Find the measure of each angle. Please enter your answer as an ordered triple ( x , y , z ), where x , y , z are the measures (in degrees) of the smallest, medium, and the largest angle, respectively. Please do not include the units in your answer.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the system. 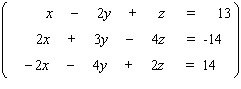
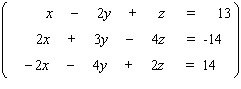

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
63
Part of $5,000 is invested at 9%, another part at 10%, and the remainder at 11% yearly interest. The total yearly income from the three investments is $505. The sum of the amounts invested at 9% and 10% equals the amount invested at 11%. How much is invested at each rate? Please enter your answer as an ordered triple ( x , y , z ), where x , y , z are the amounts invested at 9%, 10%, and 11%, respectively. Please do not include units in your answer. $__________, $__________, $__________

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the system. 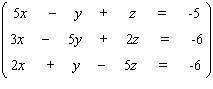

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system. 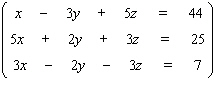

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the system. 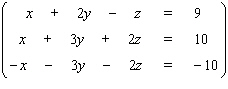
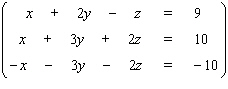

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
67
The matrix is in reduced echelon form.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
68
The augmented matrix of a system of equations is a matrix of the coefficients of the equations.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the system. 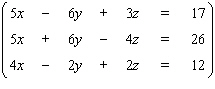
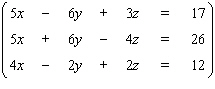

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
70
The matrix is in echelon form.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
71
A gift store is making a mixture of almonds, pecans, and peanuts, which sell for $2.50 per pound, $4.00 per pound, and $1.00 per pound, respectively. The storekeeper wants to make 20 pounds of the mix to sell at $1.90 per pound. The number of pounds of peanuts is to be three times the number of pounds of pecans. Find the number of pounds of each to be used in the mixture. Please enter your answer as an ordered triple ( x , y , z ), where x , y , z are the numbers of pounds of almonds, pecans, and peanuts, respectively.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
72
Transformations that are applied to augemented matrices are called elemtary row operations.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the system. 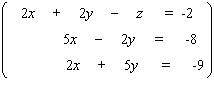
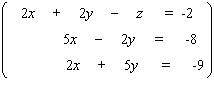

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
74
A box contains $7.40 in nickels, dimes, and quarters. There are 44 coins in all, and the sum of the numbers of nickels and dimes is two less than the number of quarters. How many coins of each kind are there? Please enter your answer as an ordered triple ( x , y , z ), where x , y , z are the numbers of nickels, dimes, and quarters, respectively.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
75
A matrix of dimension has 3 rows and 4 columns.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the system. 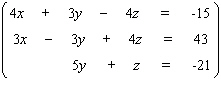
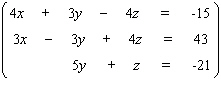

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the system. 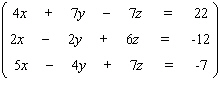
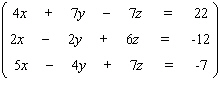

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the system. 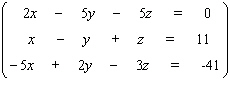
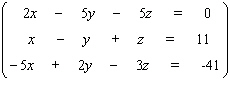

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the system. 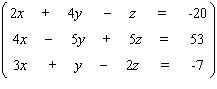
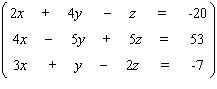

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
80
A small company makes three different types of bird houses. Each type requires the services of three different departments, as indicated by the following table. Type A Type B Type C Cutting department 0.1 hour 0.1 hour 0.2 hour Finishing department 0.5 hour 0.5 hour 0.3 hour Assembly department 0.3 hour 0.1 hour 0.2 hour The cutting, finishing, and assembly departments have available a maximum of 27, 86, and 37 work-hours per week, respectively. How many bird houses of each type should be made per week so that the company is operating at full capacity? Please enter your answer as an ordered triple ( x , y , z ), where x , y , z are the numbers of houses of type A, B, and C, respectively.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck


