Deck 11: Exponential and Logarithmic Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 11: Exponential and Logarithmic Functions
1
Solve the equation.
A)x = 6
B)x = -4
C)x = -6
D)x = -5
E)x = 4
A)x = 6
B)x = -4
C)x = -6
D)x = -5
E)x = 4
x = -4
2
Graph the exponential function.
A)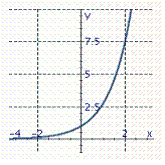
B)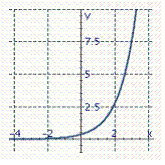
C)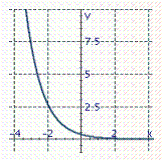
D)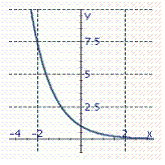
A)

B)

C)

D)


3
Suppose that the present population of a city is 550,000. Use the equation P ( t )= 550,000 e 0.034 t to estimate future growth. Estimate the population 50 years from now.
A)P = 3,012,651
B)P = 3,010,671
C)P = 3,010,093
D)P = 3,010,805
E)P = 3,010,950
A)P = 3,012,651
B)P = 3,010,671
C)P = 3,010,093
D)P = 3,010,805
E)P = 3,010,950
P = 3,010,671
4
Complete the following chart, which illustrates what happens to $8,000 invested at 12% for different lengths of time and different numbers of compounding periods. Round all of your answers to the nearest dollar.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
Complete the following chart, which illustrates what happens to $16,000 invested at various rates of interest for different lengths of time but always compounded continuously. Round your answers to the nearest dollar.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose that Nora invested $400 at 8.5% compounded annually for 6 years and Patti invested $400 at 8% compounded quarterly for 6 years. At the end of 6 years, who will have the most money and by how much (to the nearest dollar)?
A)Patti by $9
B)Nora by $1
C)Patti by $1
D)Nora by $9
E)They will have equal amounts of money.
A)Patti by $9
B)Nora by $1
C)Patti by $1
D)Nora by $9
E)They will have equal amounts of money.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that a certain radioactive substance has a half-life of 45 years. If there are presently 1,920 milligrams of the substance, how much, to the nearest milligram, will remain after 180 years?
A)Q = 130 milligram
B)Q = 120 milligram
C)Q = 135 milligram
D)Q = 95 milligram
E)Q = 125 milligram
A)Q = 130 milligram
B)Q = 120 milligram
C)Q = 135 milligram
D)Q = 95 milligram
E)Q = 125 milligram

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the equation.
A)x = -3
B)x = 2
C)x = -2
D)x = 4
E)x = -4
A)x = -3
B)x = 2
C)x = -2
D)x = 4
E)x = -4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the exponential function. f ( x )= 3 x
A)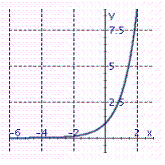
B)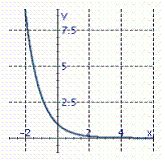
C)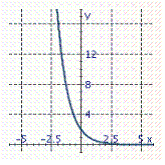
D)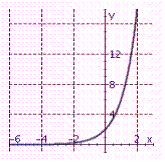
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
Graph the exponential function. f ( x )= 3 x + 2
A)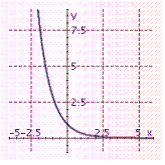
B)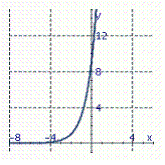
C)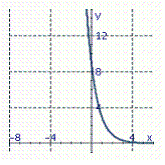
D)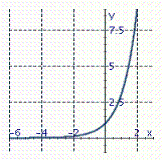
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the function.
A)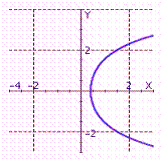
B)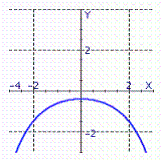
C)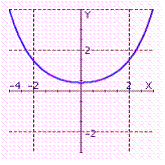
D)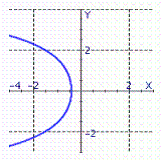
E)none of these
A)

B)

C)

D)

E)none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
The number of bacteria present at a given time under certain conditions is given by the equation Q = 4,000 e 0.01 t , where t is expressed in minutes. How many bacteria are present at the end of 45 minutes? Please round the answers to the nearest whole.
A)Q = 6,344 bacteria
B)Q = 6,273 bacteria
C)Q = 6,287 bacteria
D)Q = 6,298 bacteria
E)Q = 6,282 bacteria
A)Q = 6,344 bacteria
B)Q = 6,273 bacteria
C)Q = 6,287 bacteria
D)Q = 6,298 bacteria
E)Q = 6,282 bacteria

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
The half-life of radium is approximately 1,600 years. If the present amount of radium in a certain location is 900 grams, how much will remain after 400 years? Express your answer to the nearest gram.
A)Q = 734 gram
B)Q = 768 gram
C)Q = 757 gram
D)Q = 752 gram
E)Q = 744 gram
A)Q = 734 gram
B)Q = 768 gram
C)Q = 757 gram
D)Q = 752 gram
E)Q = 744 gram

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
The number of grams Q of a certain radioactive substance present after t seconds is given by the equation . How many grams remain after 17 seconds? Please round the answers to the nearest whole.
A)Q = 1,355 grams
B)Q = 1,329 grams
C)Q = 1,536 grams
D)Q = 1,278 grams
E)Q = 1,279 grams
A)Q = 1,355 grams
B)Q = 1,329 grams
C)Q = 1,536 grams
D)Q = 1,278 grams
E)Q = 1,279 grams

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
Graph the exponential function. f ( x )= e x - 5
A)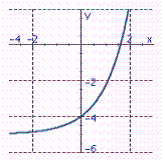
B)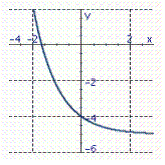
C)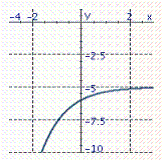
D)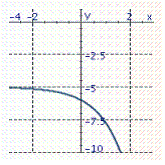
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
Write 2 9 = 512 in logarithmic form. For example, 2 3 = 8 becomes log 2 8 = 3 in logarithmic form.
A)log 2 9 = 512
B)log 512 2 = 9
C)log 512 9 = 2
D)log 2 512 = 9
E)log 9 512 = 2
A)log 2 9 = 512
B)log 512 2 = 9
C)log 512 9 = 2
D)log 2 512 = 9
E)log 9 512 = 2

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose that in a certain culture, the equation expresses the number of bacteria present as a function of the time t , where t is expressed in hours. How many bacteria are present at the end of 2 hours? The choices are rounded to the nearest whole.
A)3,670 bacteria
B)6,605 bacteria
C)1,631 bacteria
D)906 bacteria
E)2,446 bacteria
A)3,670 bacteria
B)6,605 bacteria
C)1,631 bacteria
D)906 bacteria
E)2,446 bacteria

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Graph the exponential function.
A)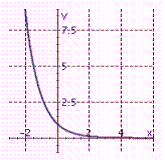
B)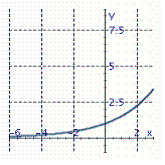
C)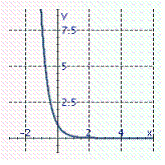
D)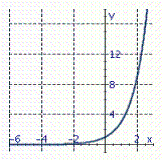
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
Write 10 6 = 1,000,000 in logarithmic form. For example, 2 3 = 8 becomes log 2 8 = 3 in logarithmic form.
A)log 10 6 = 1,000,000
B)log 6 1,000,000 = 10
C)log 1,000,000 10 = 6
D)log 1,000,000 6 = 10
E)log 10 1,000,000 = 6
A)log 10 6 = 1,000,000
B)log 6 1,000,000 = 10
C)log 1,000,000 10 = 6
D)log 1,000,000 6 = 10
E)log 10 1,000,000 = 6

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the equation log 9 x + log 9 ( x - 24)= 2.
A)x = 29
B)x = -3
C)x = 27
D)x = 3
E)x = 729
A)x = 29
B)x = -3
C)x = 27
D)x = 3
E)x = 729

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Use your calculator to find x when given ln x . Express answer to four decimal places.
A)1.8672
B)1.8072
C)1.8472
D)1.8172
E)1.8372
A)1.8672
B)1.8072
C)1.8472
D)1.8172
E)1.8372

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the equation log 6 x = 2.
A)x = 64
B)x = 42
C)x = 2
D)x = 6
E)x = 36
A)x = 64
B)x = 42
C)x = 2
D)x = 6
E)x = 36

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
Graph the function . Remember that the graph of is given. 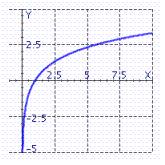
A)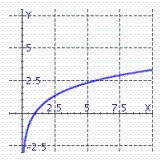
B)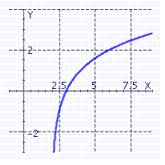
C)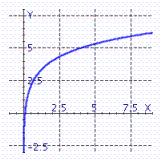

A)

B)

C)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the following.
A)8
B)1
C)6
D)0
E)none of these
A)8
B)1
C)6
D)0
E)none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Write the following equation in logarithmic form. For example, 2 3 = 8 becomes log 2 8 = 3 in logarithmic form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the equation log 3 x + log 32 = 2.
A)x = 18
B)x = 5.5
C)x = 4.5
D)x = 5
E)x = 4
A)x = 18
B)x = 5.5
C)x = 4.5
D)x = 5
E)x = 4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the logarithmic equation. Check the solution.
A)x = 1
B)x = 0
C)x = 3
D)x = 4
A)x = 1
B)x = 0
C)x = 3
D)x = 4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the logarithmic equation. Check the solution.
A)x = 9
B)x = 8
C)x = 11
D)x = 10
A)x = 9
B)x = 8
C)x = 11
D)x = 10

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
Graph by reflecting the graph of across the line y = x .
A)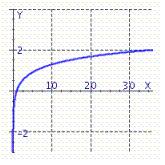
B)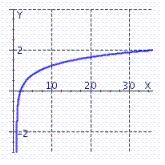
C)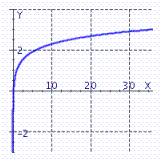
A)

B)

C)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
Graph by graphing .
A)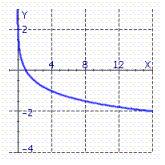
B)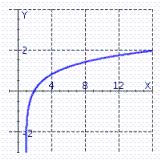
C)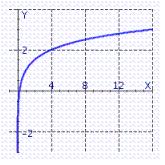
A)

B)

C)


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the logarithmic equation. Check the solution.
A) 1,000
B) 100
C) 10,000
D) 10
E) 1
A) 1,000
B) 100
C) 10,000
D) 10
E) 1

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Use a calculator and the change-of-base formula to find the logarithm to four decimal places.
A)0.5769
B)- 1.0000
C)1.1005
D)- 1.0078
E)1.7654
A)0.5769
B)- 1.0000
C)1.1005
D)- 1.0078
E)1.7654

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the equation.
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the following.
A)0
B)
C)1
D)
E)none of these
A)0
B)
C)1
D)
E)none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
Assume that , , , and are positive numbers Use the properties of logarithms to write the expression in terms of the logarithms of , , and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Assume that , , , and are positive numbers.Use the properties of logarithms to write the expression in terms of the logarithms of x , y , and z .
A)log b x log b y log b z
B)log b x + log b y + log b z
C)- log b x - log b y - log b z
D)log b x - log b y - log b z
A)log b x log b y log b z
B)log b x + log b y + log b z
C)- log b x - log b y - log b z
D)log b x - log b y - log b z

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the equation.
A)x = 2
B)x = 68
C)x = 16
D)x = 81
E)x = 64
A)x = 2
B)x = 68
C)x = 16
D)x = 81
E)x = 64

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the expression log 9 (log 2 8).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the equation log 3 (2 x - 1)- log 3 ( x - 2)= 1.
A)x = 4
B)x = 5
C)x = 2
D)x = 7
E)x = 6
A)x = 4
B)x = 5
C)x = 2
D)x = 7
E)x = 6

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
Find the value of .
A)9
B)
C)2
D)
E)
A)9
B)
C)2
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
Find the value of .
A)3
B)5
C)6
D)2
E)4
A)3
B)5
C)6
D)2
E)4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
How long will it take $700 to double itself if it is invested at 13% interest compounded semiannually? Please round the answer to the nearest tenth.
A)5.5 years
B)8.5 years
C)6.0 years
D)4.5 years
E)6.5 years
A)5.5 years
B)8.5 years
C)6.0 years
D)4.5 years
E)6.5 years

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the exponential equation and express solution to the nearest hundredth.
A)x = 2.37
B)x = 2.97
C)x = 2.47
D)x = 2.67
E)x = 2.57
A)x = 2.37
B)x = 2.97
C)x = 2.47
D)x = 2.67
E)x = 2.57

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
A principal sum of money P is invested at the end of each year in an annuity earning annual interest at a rate of r . The amount in the annuity account will be A dollars after n years, where If $2,000 is invested each year in an annuity earning 9% annual interest, how long will it take for the account to be worth $15,000? Round the answer to the nearest tenth of the year.
A)7.5 years
B)6.0 years
C)4.2 years
D)6.7 years
E)5.1 years
A)7.5 years
B)6.0 years
C)4.2 years
D)6.7 years
E)5.1 years

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Use your calculator to find x when given ln x . Express answer to four decimal places.
A)12.4018
B)12.3418
C)12.3818
D)12.3518
E)12.3718
A)12.4018
B)12.3418
C)12.3818
D)12.3518
E)12.3718

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the exponential equation and express approximate solutions to the nearest hundredth. e x - 4 = 38
A)x = 7.11
B)x = 4.00
C)x = 8.17
D)x = 7.64
E)x = 7.52
A)x = 7.11
B)x = 4.00
C)x = 8.17
D)x = 7.64
E)x = 7.52

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
Use a calculator and the change-of-base formula to find the logarithm to four decimal places.
A)0.6189
B)1.0420
C)1.8074
D)1.0342
E)0.9415
A)0.6189
B)1.0420
C)1.8074
D)1.0342
E)0.9415

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the equation.
A)x = -4
B)x = 2
C)x = 3
D)x = 4
E)x = -2
A)x = -4
B)x = 2
C)x = 3
D)x = 4
E)x = -2

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
Use your calculator to find x when given ln x . Express answer to four decimal places.
A)0.1059
B)0.1259
C)0.1559
D)0.1359
E)0.0959
A)0.1059
B)0.1259
C)0.1559
D)0.1359
E)0.0959

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Use a calculator and the change-of-base formula to find the logarithm to four decimal places. 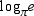
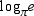

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Calculate how many times more intense an earthquake with a Richter number of 8.3 is than an earthquake with a Richter number of 6.9. Please round the answer to the whole number.
A)30
B)33
C)25
D)35
E)27
A)30
B)33
C)25
D)35
E)27

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
An earthquake in the Japan in 2011 was about 10 9 times as intense as the reference intensity. Find the Richter number for that earthquake. NOTE: Seismologists use the Richter scale to measure and report the magnitude of earthquakes. The equation compares the intensity I of an earthquake to a minimum or reference intensity I 0.
A)109
B)10
C)9
D)none of these
A)109
B)10
C)9
D)none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
Business equipment is often depreciated using the double declining-balance method. In this method, a piece of equipment with a life expectancy of N years, costing C dollars, will depreciate to a value of V dollars in n years, where n is given by the formula: A computer that cost $10,000 has a life expectancy of 5 years. If it has depreciated to a value of $2,000, how old is it? Round the answer to the nearest tenth of the year.
A)3.2 years old
B)2.2 years old
C)1.9 years old
D)2.5 years old
E)2.8 years old
A)3.2 years old
B)2.2 years old
C)1.9 years old
D)2.5 years old
E)2.8 years old

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
An earthquake has a period of second, and an amplitude of micrometers. Find its measure on the Richter scale.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the logarithmic equation. Check the solution.
A) 10
B) 27
C) 6.
D) 6
E) 8
A) 10
B) 27
C) 6.
D) 6
E) 8

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
Use the change of base formula to identify the expression that is equivalent to .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck


