Deck 9: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/163
Play
Full screen (f)
Deck 9: Probability
1
P ( A or B ) means which of the following?
A) P ( A ) P ( B )
P ( B )
B) P ( A ) P ( B )
P ( B )
C) P ( A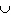 B )
B )
D) P ( A ) + P ( B )
E) P ( A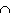 B )
B )
A) P ( A )
 P ( B )
P ( B )B) P ( A )
 P ( B )
P ( B )C) P ( A
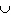 B )
B )D) P ( A ) + P ( B )
E) P ( A
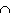 B )
B )C
2
Last year, 1,328 calculators were returned to the manufacturer. If 79,000 were produced, assign a number to specify the probability that a particular calculator would be returned. Give the probability in decimal form (correct to two decimal places). 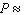 __________
__________
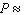 __________
__________0.02
3
FIGURE 2.  Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be even. Give the answer as an exact fraction. P (even)
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be even. Give the answer as an exact fraction. P (even)
A) P (even) =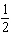
B) P (even) =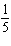
C) P (even) =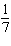
D) P (even) =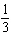
E) P (even) =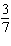
 Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be even. Give the answer as an exact fraction. P (even)
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be even. Give the answer as an exact fraction. P (even)A) P (even) =
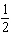
B) P (even) =
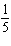
C) P (even) =
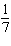
D) P (even) =
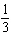
E) P (even) =
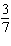
A
4
The game of Dungeons and Dragons uses nonstandard dice. Consider a die with eight sides marked 1, 2, 3, 4, 5, 6, 7, and 8. (In this problem, "an eight" refers to rolling an eight on either or both dice, while "a total of eight" refers to the sum on the two dice.) List the sample space for yourself in order to answer the following question. What is the probability of rolling exactly one seven with two such dice?
A)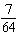
B)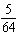
C)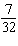
D)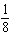
E)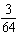
A)
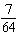
B)
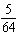
C)
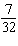
D)
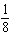
E)
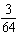

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
5
In a game of dice, a player loses if the outcome of the first roll is a two, three, or twelve. (This refers to the total of the two dice.) What is the probability of a total of three on the first roll?
A)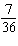
B)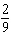
C)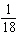
D)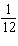
E)
A)
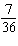
B)
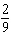
C)
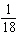
D)
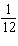
E)


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose you flip 3 coins simultaneously. List the sample space for yourself in order to answer the question. What is the probability of all 3 coins being heads?
A)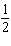
B)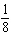
C)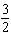
D)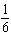
E)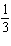
A)
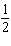
B)
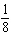
C)
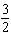
D)
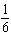
E)
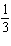

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
7
P ( A and B ) means which of the following?
A) P ( A ) P ( B )
P ( B )
B) P ( A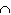 B )
B )
C) P ( A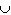 B )
B )
D) P ( A ) + P ( B )
E) P ( A ) P ( B )
P ( B )
A) P ( A )
 P ( B )
P ( B )B) P ( A
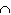 B )
B )C) P ( A
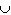 B )
B )D) P ( A ) + P ( B )
E) P ( A )
 P ( B )
P ( B )
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
8
FIGURE 1. 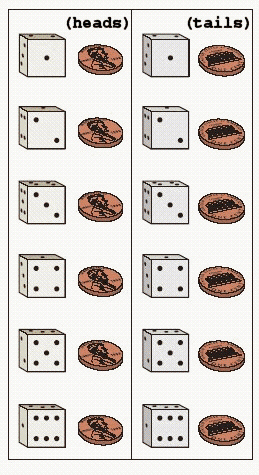 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails?
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails?
A) P (Tails) =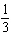
B) P (Tails) =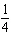
C) P (Tails) =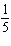
D) P (Tails) =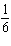
E) P (Tails) =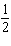
 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails?
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails?A) P (Tails) =
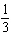
B) P (Tails) =
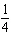
C) P (Tails) =
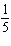
D) P (Tails) =
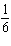
E) P (Tails) =
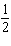

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
9
For the spinners in the figure below, assume that the pointer can never lie on a border line. Find 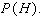
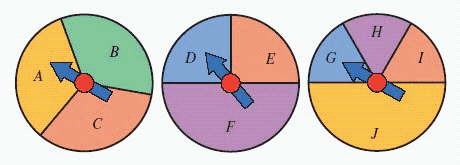
A)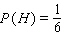
B)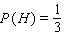
C)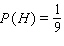
D)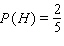
E)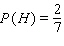
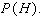

A)
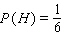
B)
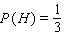
C)
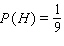
D)
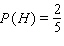
E)
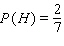

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
10
FIGURE 1. 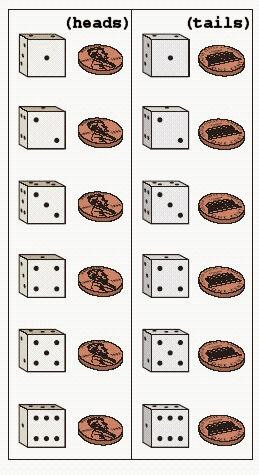 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining heads and a two?
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining heads and a two?
A)
B)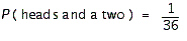
C)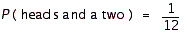
D)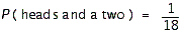
E)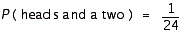
 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining heads and a two?
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining heads and a two?A)

B)
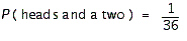
C)
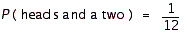
D)
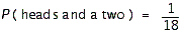
E)
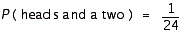

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
11
Poker is a common game in which players are dealt five cards from a deck of cards. It can be shown that there are 2,598,960 different possible poker hands. The winning hands (from highest to lowest) are shown in the table below. Royal Flush 4 hands 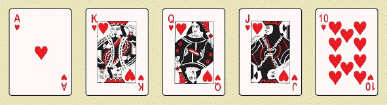 Other straight flush 36 hands
Other straight flush 36 hands  Four of a kind 624 hands
Four of a kind 624 hands  Full house 3,744 hands
Full house 3,744 hands  Flush 5,108 hands
Flush 5,108 hands  Straight 10,200 hands
Straight 10,200 hands 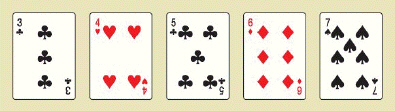 Three of a kind 54,912 hands
Three of a kind 54,912 hands 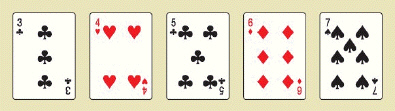 Two pair 123,552 hands
Two pair 123,552 hands  One pair 1,098,240 hands
One pair 1,098,240 hands  Other hands 1,302,540 hands
Other hands 1,302,540 hands  Find the requested probabilities. Use a calculator. Select the pair of answers closest to the answers on your calculator. P (royal flush)
Find the requested probabilities. Use a calculator. Select the pair of answers closest to the answers on your calculator. P (royal flush)  __________ P (straight flush)
__________ P (straight flush)  __________
__________
A) P (royal flush) 0.0000015; P (straight flush)
0.0000015; P (straight flush)  0.0000139
0.0000139
B) P (royal flush) 0.0000002; P (straight flush)
0.0000002; P (straight flush) 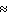 0.0000014
0.0000014
C) P (royal flush)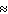 0.0000015; P (straight flush)
0.0000015; P (straight flush) 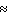 0.0000014
0.0000014
D) P (royal flush)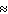 0.0000002; P (straight flush)
0.0000002; P (straight flush) 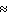 0.0000139
0.0000139
E) P (royal flush)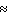 0.0000139; P (straight flush)
0.0000139; P (straight flush) 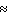 0.0000015
0.0000015
 Other straight flush 36 hands
Other straight flush 36 hands  Four of a kind 624 hands
Four of a kind 624 hands  Full house 3,744 hands
Full house 3,744 hands  Flush 5,108 hands
Flush 5,108 hands  Straight 10,200 hands
Straight 10,200 hands  Three of a kind 54,912 hands
Three of a kind 54,912 hands  Two pair 123,552 hands
Two pair 123,552 hands  One pair 1,098,240 hands
One pair 1,098,240 hands  Other hands 1,302,540 hands
Other hands 1,302,540 hands  Find the requested probabilities. Use a calculator. Select the pair of answers closest to the answers on your calculator. P (royal flush)
Find the requested probabilities. Use a calculator. Select the pair of answers closest to the answers on your calculator. P (royal flush) 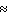 __________ P (straight flush)
__________ P (straight flush) 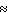 __________
__________A) P (royal flush)
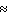 0.0000015; P (straight flush)
0.0000015; P (straight flush) 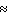 0.0000139
0.0000139B) P (royal flush)
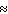 0.0000002; P (straight flush)
0.0000002; P (straight flush) 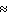 0.0000014
0.0000014C) P (royal flush)
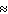 0.0000015; P (straight flush)
0.0000015; P (straight flush) 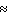 0.0000014
0.0000014D) P (royal flush)
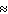 0.0000002; P (straight flush)
0.0000002; P (straight flush) 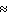 0.0000139
0.0000139E) P (royal flush)
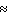 0.0000139; P (straight flush)
0.0000139; P (straight flush) 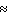 0.0000015
0.0000015
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
12
Last year in Ferndale, CA, it rained on 28 days. What is the probability of rain on a day selected at random? Give the probability in decimal form (correct to two decimal places).
A) about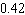
B) about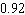
C) about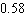
D) about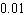
E) about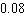
A) about
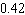
B) about
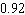
C) about
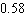
D) about
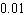
E) about
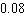

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
13
Dice is a popular game in gambling casinos. Two dice are tossed, and various amounts are paid according to the outcome. If a seven or eleven occurs on the first roll, the player wins. If a player tosses a pair of ones (called snake eyes ) on the first roll, the player loses. What is the probability of tossing a seven on the first roll?
A)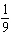
B)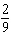
C)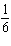
D)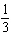
E)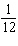
A)
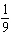
B)
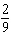
C)
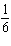
D)
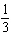
E)
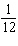

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
14
FIGURE 2.  Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to seven:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to seven: 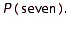 Give the answer as an exact fraction.
Give the answer as an exact fraction.
A)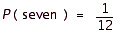
B)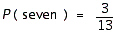
C)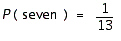
D)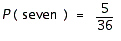
E)
 Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to seven:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to seven: 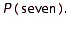 Give the answer as an exact fraction.
Give the answer as an exact fraction.A)
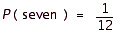
B)
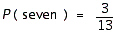
C)
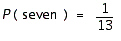
D)
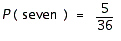
E)


Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
15
A single card is selected from an ordinary deck of cards. The sample space is shown in the figure below. 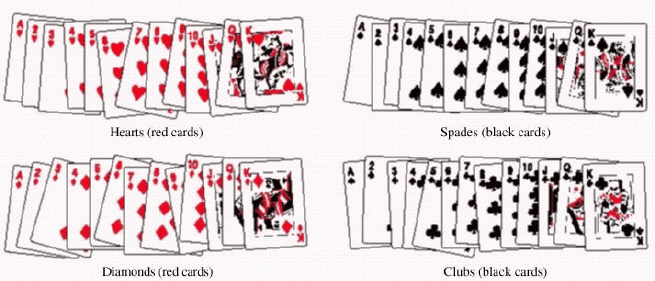 Find the probability P ( red face card )
Find the probability P ( red face card )
A)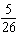
B)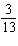
C)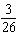
D)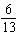
E)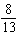
 Find the probability P ( red face card )
Find the probability P ( red face card )A)
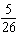
B)
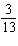
C)
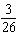
D)
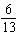
E)
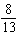

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
16
Last year, 1,394 calculators were returned to the manufacturer. If 72,000 were produced, assign a number to specify the probability that a particular calculator would be returned. Give the probability in decimal form (correct to two decimal places).
A) about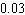
B) about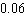
C) about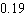
D) about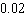
E) about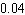
A) about
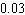
B) about
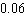
C) about
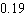
D) about
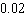
E) about
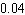

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
17
If you simultaneously toss a coin and roll a die, the possible outcomes are H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, and T6. What is the probability of a head and an odd number?
A)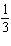
B)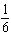
C)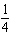
D)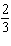
E)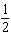
A)
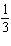
B)
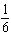
C)
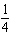
D)
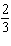
E)
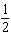

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
18
FIGURE 2.  Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to five:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to five: 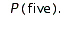 Give the answer as an exact fraction.
Give the answer as an exact fraction.
A)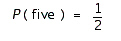
B)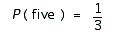
C)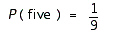
D)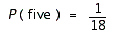
E)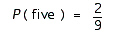
 Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to five:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to five: 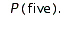 Give the answer as an exact fraction.
Give the answer as an exact fraction.A)
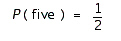
B)
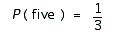
C)
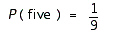
D)
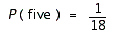
E)
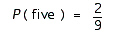

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
19
The campus vets club is having a raffle and is selling 3,000 tickets. If the people on the floor of your dorm bought 360 tickets, what is the probability that someone on your floor will hold the winning ticket? Give the probability in decimal form (correct to two decimal places).
A) about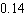
B) about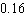
C) about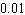
D) about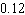
E) about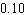
A) about
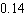
B) about
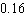
C) about
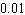
D) about
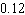
E) about
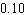

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
20
Last year, a certain professor gave 44 F grades out of 882 grades. If one of the professor's students were selected randomly, what is the probability of the student receiving an F? Give the probability in decimal form (correct to two decimal places).
A) about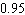
B) about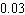
C) about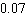
D) about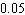
E) about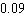
A) about
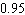
B) about
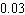
C) about
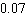
D) about
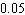
E) about
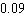

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
21
Last year in Ferndale, CA, it rained on 41 days. What is the probability of rain on a day selected at random? Give the probability in decimal form (correct to two decimal places). 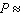 __________
__________
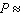 __________
__________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
22
Last year, a certain professor gave 59 A grades out of 849 grades. If one of the professor s students were selected randomly, what is the probability of the student receiving an A? Give the probability in decimal form (correct to two decimal places). 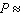 __________
__________
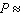 __________
__________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
23
For the spinners in the figure below, assume that the pointer can never lie on a border line. Find 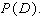 Give your answer as a fraction.
Give your answer as a fraction. 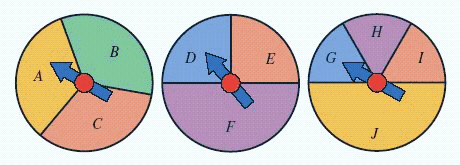
 Give your answer as a fraction.
Give your answer as a fraction. 

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
24
FIGURE 1.  Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails or a five? Give your answer as a fraction.
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails or a five? Give your answer as a fraction.
 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails or a five? Give your answer as a fraction.
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails or a five? Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose you flip 3 coins simultaneously. List the sample space for yourself in order to answer the question. What is the probability of all 3 coins being tails? Give your answer as a fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
26
In a game of dice, a player loses if the outcome of the first roll is a two, three, or twelve. (This refers to the total of the two dice.) What is the probability of losing on the first roll? Give your answer as a fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
27
Dice is a popular game in gambling casinos. Two dice are tossed, and various amounts are paid according to the outcome. If a seven or eleven occurs on the first roll, the player wins. If a player tosses a pair of ones (called snake eyes ) on the first roll, the player loses. What is the probability of winning on the first roll?
Give your answer as a fraction.
Give your answer as a fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
28
FIGURE 2.  Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to eight:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to eight:  Give your answer as a fraction.
Give your answer as a fraction.
 Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to eight:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice that add to eight:  Give your answer as a fraction.
Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
29
FIGURE 3. 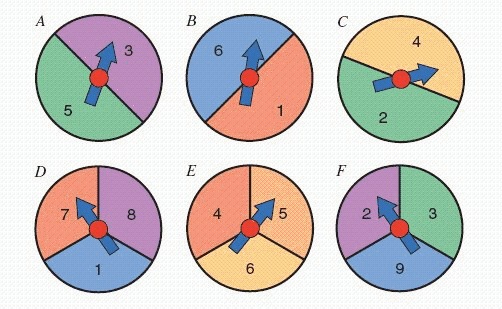 Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?
Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?  plays
plays  __________ (Answer C , A , or either; it s a draw)
__________ (Answer C , A , or either; it s a draw)
 Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?
Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?  plays
plays  __________ (Answer C , A , or either; it s a draw)
__________ (Answer C , A , or either; it s a draw)
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
30
FIGURE 3. 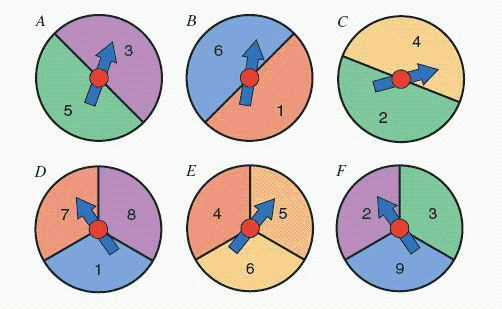 Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?
Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose? 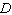 plays
plays 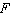 __________ (Answer F , D or either; it s a draw )
__________ (Answer F , D or either; it s a draw )
 Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose?
Refer to Figure 3. Suppose you and an opponent both pick one of the spinners in the figure. A win means spinning a higher number. Based on the probability of a win, which of the two spinners would you choose? 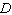 plays
plays 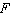 __________ (Answer F , D or either; it s a draw )
__________ (Answer F , D or either; it s a draw )
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
31
FIGURE 1. 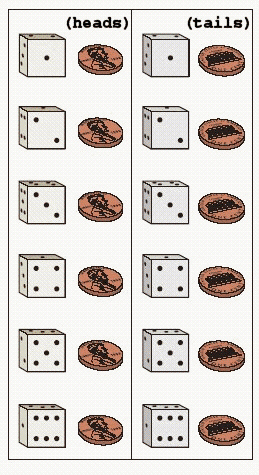 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails? Give your answer as a fraction.
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails? Give your answer as a fraction.
 Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails? Give your answer as a fraction.
Refer to Figure 1. Suppose that you toss a coin and roll a die. The sample space is shown in the figure. What is the probability of obtaining tails? Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
32
The campus vets club is having a raffle and is selling 2,500 tickets. If the people on the floor of your dorm bought 495 tickets, what is the probability that someone on your floor will hold the winning ticket? Give the probability in decimal form (correct to two decimal places). 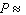 __________
__________
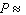 __________
__________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
33
The game of Dungeons and Dragons uses nonstandard dice. Consider a die with eight sides marked 1, 2, 3, 4, 5, 6, 7, and 8. (In this problem, "an eight" refers to rolling an eight on either or both dice, while "a total of eight" refers to the sum on the two dice.) What is the probability of rolling exactly one two with two such dice?
Give your answer as a fraction.
Give your answer as a fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
34
For the spinners in the figure below, assume that the pointer can never lie on a border line. Find 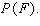 Give your answer as a fraction.
Give your answer as a fraction. 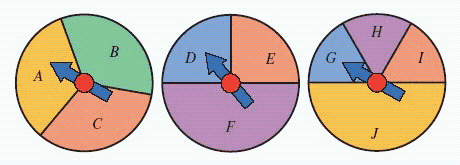
 Give your answer as a fraction.
Give your answer as a fraction. 

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose you simultaneously toss a coin and roll a die. The possible outcomes are H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, and T6. What is the probability of a three? Give your answer as a reduced fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the following statement.
Answer true or false . P ( A or B ) means P ( A B )
B )
Answer true or false . P ( A or B ) means P ( A
 B )
B )
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
37
FIGURE 2.  Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be four or five:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be four or five: 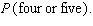 Give your answer as a fraction.
Give your answer as a fraction.
 Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be four or five:
Refer to Figure 2. Use the sample space shown in the figure to find the probability of rolling two dice and having the sum be four or five: 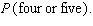 Give your answer as a fraction.
Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the following statement.
Answer true or false . P ( A and B ) means P ( A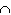 B )
B )
Answer true or false . P ( A and B ) means P ( A
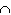 B )
B )
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
39
Poker is a common game in which players are dealt five cards from a deck of cards. It can be shown that there are 2,598,960 different possible poker hands. The winning hands (from highest to lowest) are shown in the table below. Royal flush 4 hands 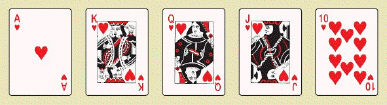 Other straight flush 36 hands
Other straight flush 36 hands  Four of a kind 624 hands
Four of a kind 624 hands  Full house 3,744 hands
Full house 3,744 hands  Flush 5,108 hands
Flush 5,108 hands  Straight 10,200 hands
Straight 10,200 hands 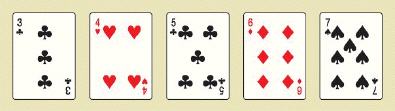 Three of a kind 54,912 hands
Three of a kind 54,912 hands 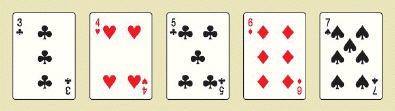 Two pair 123,552 hands
Two pair 123,552 hands 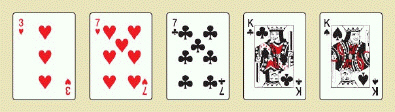 One pair 1,098,240 hands
One pair 1,098,240 hands 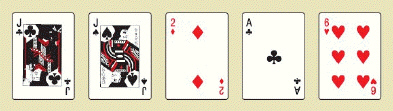 Other hands 1,302,540 hands
Other hands 1,302,540 hands 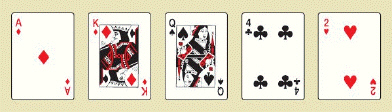 Find the requested probabilities. Use a calculator and show your answers to whatever accuracy possible on your calculator. P (two pair) = __________ P (one pair) = __________
Find the requested probabilities. Use a calculator and show your answers to whatever accuracy possible on your calculator. P (two pair) = __________ P (one pair) = __________
 Other straight flush 36 hands
Other straight flush 36 hands  Four of a kind 624 hands
Four of a kind 624 hands  Full house 3,744 hands
Full house 3,744 hands  Flush 5,108 hands
Flush 5,108 hands  Straight 10,200 hands
Straight 10,200 hands  Three of a kind 54,912 hands
Three of a kind 54,912 hands  Two pair 123,552 hands
Two pair 123,552 hands  One pair 1,098,240 hands
One pair 1,098,240 hands  Other hands 1,302,540 hands
Other hands 1,302,540 hands  Find the requested probabilities. Use a calculator and show your answers to whatever accuracy possible on your calculator. P (two pair) = __________ P (one pair) = __________
Find the requested probabilities. Use a calculator and show your answers to whatever accuracy possible on your calculator. P (two pair) = __________ P (one pair) = __________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
40
A single card is selected from an ordinary deck of cards. The sample space is shown in the figure below. 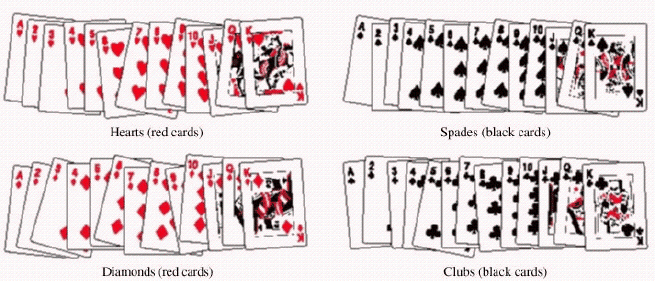 Find the probability P(heart and a jack). Give your answer as a fraction.
Find the probability P(heart and a jack). Give your answer as a fraction.
 Find the probability P(heart and a jack). Give your answer as a fraction.
Find the probability P(heart and a jack). Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose a restaurant offers the following prix fixe menu:  How many different dinners can this restaurant serve?
How many different dinners can this restaurant serve?
A)
B)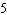
C)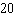
D)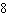
E)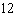
 How many different dinners can this restaurant serve?
How many different dinners can this restaurant serve?A)
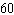
B)
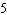
C)
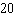
D)
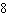
E)
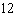

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
42
If a state issued license plates using the scheme of two letters followed by five digits, how many plates could it issue?
A)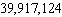 plates
plates
B)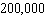 plates
plates
C)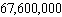 plates
plates
D)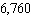 plates
plates
E)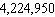 plates
plates
A)
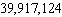 plates
platesB)
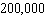 plates
platesC)
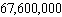 plates
platesD)
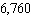 plates
platesE)
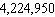 plates
plates
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
43
How many shirt-blouse outfits can a woman wear if she has 5 skirts and 6 blouses?
A)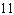 outfits
outfits
B)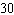 outfits
outfits
C)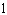 outfits
outfits
D)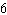 outfits
outfits
E)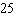 outfits
outfits
A)
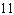 outfits
outfitsB)
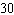 outfits
outfitsC)
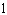 outfits
outfitsD)
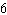 outfits
outfitsE)
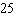 outfits
outfits
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
44
Complete the list. 
A)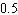
B) 0
C) 1
D)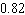
E)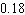

A)
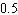
B) 0
C) 1
D)
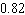
E)
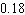

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
45
Find 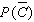 if
if 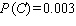 .
.
A)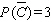
B)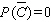
C)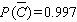
D)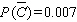
E)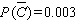
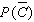 if
if 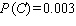 .
.A)
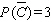
B)
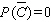
C)
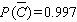
D)
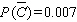
E)
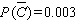

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
46
A state issued license plates using the scheme of two letters followed by five digits, and 241 letter arrangements were not allowed. How many plates could it issue?
A)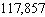 plates
plates
B)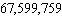 plates
plates
C)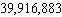 plates
plates
D)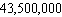 plates
plates
E)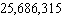 plates
plates
A)
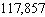 plates
platesB)
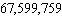 plates
platesC)
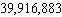 plates
platesD)
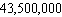 plates
platesE)
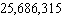 plates
plates
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
47
In your mathematics class, there are 28 students who attended class on the first day of the semester. 19 of the students brought a calculator to class that first day. If a student is randomly selected, what is the probability that student brought a calculator the first day?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
48
What is the probability of obtaining at least one head in 3 flips of a coin?
A)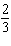
B)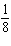
C)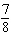
D)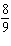
E)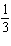
A)
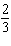
B)
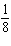
C)
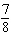
D)
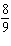
E)
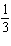

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
49
Find 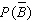 if
if 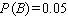 .
.
A)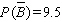
B)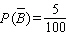
C)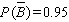
D)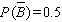
E)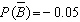
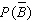 if
if 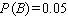 .
.A)
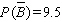
B)
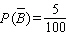
C)
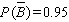
D)
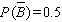
E)
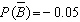

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
50
Use estimation to select the best response. Do not calculate. Which of the following is less probable?
A) Obtaining a five at least 2 times in 3 rolls of a die
B) Obtaining a five 2 times in 3 rolls of a die
C) They are equally probable
A) Obtaining a five at least 2 times in 3 rolls of a die
B) Obtaining a five 2 times in 3 rolls of a die
C) They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
51
Complete the list. 
A)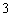
B)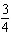
C)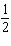
D)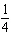
E)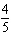

A)
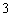
B)
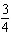
C)
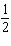
D)
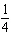
E)
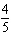

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
52
A history teacher gives an 10-question true-false exam. In how many different ways can the test be answered, if the possible answers are true or false?
A)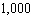
B)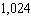
C)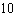
D)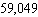
E)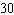
A)
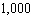
B)
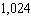
C)
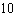
D)
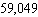
E)
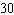

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
53
Find 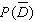 if
if 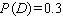 .
.
A)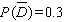
B)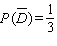
C)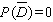
D)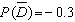
E)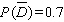
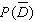 if
if 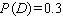 .
.A)
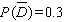
B)
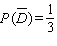
C)
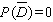
D)
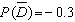
E)
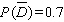

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
54
Find 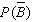 if
if 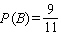 .
.
A)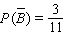
B)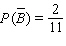
C)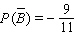
D)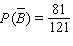
E)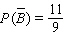
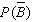 if
if 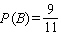 .
.A)
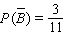
B)
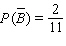
C)
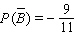
D)
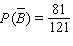
E)
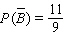

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
55
Complete the list. 
A)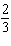
B)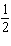
C)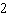
D)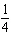
E)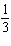

A)
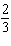
B)
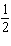
C)
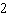
D)
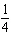
E)
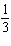

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
56
In your mathematics class, there are 12 male and 17 female students who attended class on the first day of the semester. If you randomly select a student the first day, what is the probability you selected a female?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
57
What is the probability of obtaining a sum of at least 6 when rolling a pair of dice?
A)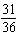
B)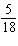
C)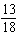
D)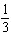
E)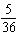
A)
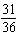
B)
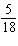
C)
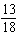
D)
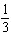
E)
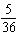

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
58
Use estimation to select the best response. Do not calculate. Which of the following is more probable?
A) Obtaining at least 2 heads in 3 flips of a coin
B) Obtaining at least 2 heads in 4 flips of a coin
C) They are equally probable
A) Obtaining at least 2 heads in 3 flips of a coin
B) Obtaining at least 2 heads in 4 flips of a coin
C) They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
59
Use estimation to select the best response. Do not calculate. Which of the following is less probable?
A) Guessing all the correct answers on a 20-question true-false examination
B) Obtaining all tails in 20 tosses of a penny
C) They are equally probable
A) Guessing all the correct answers on a 20-question true-false examination
B) Obtaining all tails in 20 tosses of a penny
C) They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
60
In your mathematics class, there are 28 students who attended class on the first day of the semester. 19 of the students brought a calculator to class that first day. If a student is randomly selected, what is the probability that student did not bring a calculator the first day?

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
61
What is the probability of obtaining at least one tail in 4 flips of a coin? Give your answer as a fraction.

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
62
How many shirt-blouse outfits can a woman wear if she has 4 skirts and 5 blouses?
__________ outfits
__________ outfits

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
63
Use estimation to select the best response. Do not calculate.
Which of the following is less probable?
Guessing all the incorrect answers on a 20-question true-false examination or
Obtaining all tails in 20 tosses of a quarter or
They are equally probable
Which of the following is less probable?
Guessing all the incorrect answers on a 20-question true-false examination or
Obtaining all tails in 20 tosses of a quarter or
They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
64
Complete the list.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
65
Find 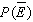 if
if 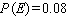 .
. 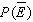 = __________
= __________
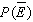 if
if 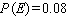 .
. 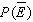 = __________
= __________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
66
Find 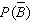 if
if 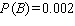 .
. 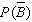 = __________
= __________
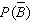 if
if 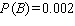 .
. 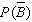 = __________
= __________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
67
What is the probability of flipping a coin 8 times and obtaining all heads?
A)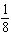
B)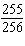
C)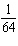
D)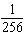
E)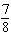
A)
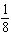
B)
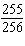
C)
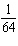
D)
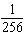
E)
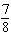

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
68
A state issued license plates using the scheme of two letters followed by three numerals. How many plates could it issue?
__________ plates
__________ plates

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
69
Complete the list. Give your answer as a fraction.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
70
Find the probability of 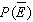 if
if 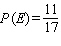 . Give your answer as a fraction.
. Give your answer as a fraction.
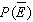 if
if 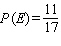 . Give your answer as a fraction.
. Give your answer as a fraction.
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
71
Use estimation to select the best response. Do not calculate.
Which of the following is more probable?
Obtaining at least 3 heads in 5 flips of a coin or
Obtaining at least 3 heads in 6 flips of a coin or
They are equally probable
Which of the following is more probable?
Obtaining at least 3 heads in 5 flips of a coin or
Obtaining at least 3 heads in 6 flips of a coin or
They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose a restaurant offers the following prix fixe menu:
 How many different dinners can this restaurant serve? __________ different dinners
How many different dinners can this restaurant serve? __________ different dinners
 How many different dinners can this restaurant serve? __________ different dinners
How many different dinners can this restaurant serve? __________ different dinners
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
73
A history teacher gives a 14-question true-false exam. In how many different ways can the test be answered if the possible answers are true or false?
__________ different ways
__________ different ways

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
74
What is the probability of a family with 6 children having 3 boys and 3 girls?
A)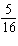
B)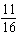
C)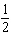
D)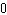
E)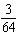
A)
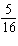
B)
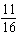
C)
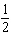
D)
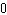
E)
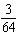

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
75
Find 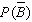 if
if 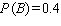
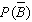 = __________
= __________
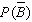 if
if 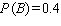
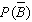 = __________
= __________
Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
76
Use estimation to select the best response. Do not calculate.
Which of the following is more probable?
Obtaining a six 3 times in 5 rolls of a die or
Obtaining a six at least 3 times in 5 rolls of a die or
They are equally probable
Which of the following is more probable?
Obtaining a six 3 times in 5 rolls of a die or
Obtaining a six at least 3 times in 5 rolls of a die or
They are equally probable

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
77
Complete the list.



Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
78
A typical Social Security identification number is 747-61-2313. How many Social Security numbers are possible if the first digit cannot be 0?
__________ numbers
__________ numbers

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
79
A state issued license plates using the scheme of three letters followed by three numerals, and 243 letter arrangements were not allowed. How many plates could it issue?
__________ plates
__________ plates

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck
80
A typical Social Security identification number is 805-83-3253. How many Social Security numbers are possible if the first digit of each group cannot be 0?
A)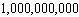
B)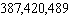
C)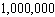
D)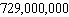
E)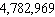
A)
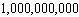
B)
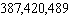
C)
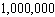
D)
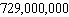
E)
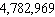

Unlock Deck
Unlock for access to all 163 flashcards in this deck.
Unlock Deck
k this deck


