Deck 12: Comparing Two Means

Question 1

If we collect blood pressure values for a set of patients before talking with a psychiatrist and then blood pressure values from the same individuals after talking with a psychiatrist, what type of test is most appropriate?

A) Paired test
B) Separation test
C) Temporal test
D) Two-sample test

Answer 1

A

Question 2

If we collect blood pressure values for a set of patients before talking with a psychiatrist and then blood pressure values from a second set of individuals after talking with a psychiatrist, what type of test is most appropriate?

A) Paired test
B) Separation test
C) Temporal test
D) Two-sample test

Answer 2

D

Question 3

When analyzing the set of differences in a paired t-test procedure, if the confidence interval for the differences does not include zero, we expect the results of our t-test to be which of the following?

A) P > 0.05 and we fail to reject the null hypothesis of equal means.
B) P > 0.05 and we reject the null hypothesis of equal means.
C) P < 0.05 and we fail to reject the null hypothesis of equal means.
D) P < 0.05 and we reject the null hypothesis of equal means.

Answer 3

D

Question 4

When doing a paired t-test, if the confidence interval for the differences includes zero, we expect the results of our t-test to be which of the following?

A) P > 0.05 and we fail to reject the null hypothesis of equal means.
B) P > 0.05 and we reject the null hypothesis of equal means.
C) P < 0.05 and we fail to reject the null hypothesis of equal means.
D) P < 0.05 and we reject the null hypothesis of equal means.

Question 5

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the difference in the mean population density values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$

A) -1.0
B) -2.0
C) -3.0
D) -4.0

Question 6

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the 95% confidence interval for the difference in the values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$

A) -7.6 < ? < 1.55
B) -6.4 < ? < 1.36
C) -5.9 < ? < -1.26
D) -5.4 < ? < -1.76

Question 7

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the 95% confidence interval for the difference in the mean values, what do you predict the results of a paired t-test to be?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$ ?

A) Fail to reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
B) Fail to reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.
C) Reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
D) Reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.

Question 8

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the t-test statistic for a paired t-test of the difference in the mean values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$

A) -1.29
B) -1.69
C) -2.09
D) -2.49

Question 9

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the t-test statistic, and using your table of critical t-values, which of the following P-value ranges matches the one for the t-value she obtains?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$

A) 0.05 < p
B) 0.02 < p < 0.05
C) 0.01 < p < 0.02
D) p < 0.01

Question 10

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the t-test statistic, which of the following best described the results of Chris's paired t-test?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 28 \\6 & 48 & 39\end{array}$ ?

A) Fail to reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
B) Fail to reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.
C) Reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
D) Reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.

Question 11

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the difference in the mean population density values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$

A) -1.0
B) -2.0
C) -3.0
D) -4.0

Question 12

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the 95% confidence interval for the difference in the values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$

A) -8.9 < ? < 0.9
B) -7.9 < ? < -0.1
C) -7.4 < ? < -0.6
D) -5.9 < ? < -2.1

Question 13

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the 95% confidence interval for the difference in the mean values, what do you predict the results of a paired t-test to be?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$ ?

A) Fail to reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
B) Fail to reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.
C) Reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
D) Reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.

Question 14

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. What is the t-test statistic for a paired t-test of the difference in the mean values?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$

A) -2.04
B) -2.54
C) -3.04
D) -3.54

Question 15

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the t-test statistic, and using your table of critical t-values, which of the following P-value ranges matches the one for the t-value she obtains?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$

A) 0.05 < p
B) 0.02 < p < 0.05
C) 0.01 < p < 0.02
D) p < 0.01

Question 16

Consider a situation in which Chris predicts that an impending drainage connection will alter the number of fish in a set of six small lakes. She uses a large net (a seine) and counts the number of fish and obtains the values shown. Based on the t-test statistic, which of the following best described the results of Chris's paired t-test?
?
Number of fish caught in six seines before and after drainage connection.

$\begin{array}{lll}\underline {\text {Vial } }&\underline {\text { Before } }&\underline {\text { After } }\\1 & 24 & 20 \\2 & 35 & 31 \\3 & 64 & 59 \\4 & 51 & 52 \\5 & 25 & 22 \\6 & 48 & 39\end{array}$ ?

A) Fail to reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
B) Fail to reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.
C) Reject the null hypothesis, the storm did not seem to change the number of fish in the lakes.
D) Reject the null hypothesis, the storm seemed to reduce the number of fish in the lakes.

Question 17

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
What is the pooled sample variance?

A) 0.099
B) 0.104
C) 0.109
D) 0.114

Question 18

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
What is the standard error of the difference between the two means?

A) 0.142
B) 0.145
C) 0.148
D) 0.151

Question 19

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
What is the 95% confidence interval for the difference between the two means?

A) 0.017 < μ₁ - μ₂ < 0.583
B) 0.010 < μ₁ - μ₂ < 0.590
C) 0.003 < μ₁ - μ₂ < 0.597
D) -0.004 < μ₁ - μ₂ < 0.604

Question 20

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
What is the t-statistic for the t-test?

A) 1.96
B) 2.06
C) 2.16
D) 2.26

Question 21

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
Based on the t-test statistic, and using your table of critical t-values, which of the following P-value ranges matches the one for the t-value?

A) 0.05 < p
B) 0.02 < p < 0.05
C) 0.01 < p < 0.02
D) p < 0.01

Question 22

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. She plans to conduct a two-sample t-test and will assume that the population variances are equal. Her data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 12
Far (group 2): mean = 5.8, SD = 0.30, n = 9
What is the conclusion of the t-test?

A) Fail to reject the null hypothesis, the mean number of eggs do not seem to differ in the two types of locations.
B) Fail to reject the null hypothesis, the mean number of eggs seem to differ in the two types of locations.
C) Reject the null hypothesis, the mean number of eggs do not seem to differ in the two types of locations.
D) Reject the null hypothesis, the mean number of eggs seem to differ in the two types of locations.

Question 23

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. He plans to conduct a two-sample t-test and will assume that the population variances are equal. His data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
What is the pooled sample variance?

A) 0.104
B) 0.109
C) 0.114
D) 0.119

Question 24

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. He plans to conduct a two-sample t-test and will assume that the population variances are equal. His data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
What is the standard error of the difference between the two means?

A) 0.142
B) 0.145
C) 0.148
D) 0.151

Question 25

Consider an urban ecologist who is interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. He plans to conduct a two-sample t-test and will assume that the population variances are equal. His data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
What is the 95% confidence interval for the difference between the two means?

A) -0.017 < m₁ - m₂ < 0.617
B) -0.004 < m₁ - m₂ < 0.604
C) 0.003 < m₁ - m₂ < 0.597
D) 0.013 < m₁ - m₂ < 0.587

Question 26

Consider urban ecologists who are interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. They plan to conduct a two-sample t-test and will assume that the population variances are equal. Their data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
What is the t-statistic for the t-test?

A) 1.83
B) 1.95
C) 2.03
D) 2.11

Question 27

Consider urban ecologists who are interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. They plan to conduct a two-sample t-test and will assume that the population variances are equal. Their data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
Based on the t-test statistic, and using your table of critical t-values, which of the following P-value ranges matches the one for the t-value?

A) 0.05 < p
B) 0.02 < p < 0.05
C) 0.01 < p < 0.02
D) p < 0.01

Question 28

Consider urban ecologists who are interested in whether the presence of high-voltage power lines influences the number of eggs laid by birds nearby. They plan to conduct a two-sample t-test and will assume that the population variances are equal. Their data are as follows:
Near (group 1): mean = 6.1, SD = 0.35, n = 9
Far (group 2): mean = 5.8, SD = 0.30, n = 12
What is the conclusion of the t-test?

A) Fail to reject the null hypothesis, the mean number of eggs do not seem to differ in the two types of locations.
B) Fail to reject the null hypothesis, the mean number of eggs seem to differ in the two types of locations.
C) Reject the null hypothesis, the mean number of eggs do not seem to differ in the two types of locations.
D) Reject the null hypothesis, the mean number of eggs seem to differ in the two types of locations.

Question 29

When we have two data sets that reveal 95% confidence intervals that differ from a hypothesized value and don't overlap, what conclusion can we make?

A) Although these groups differ from the hypothesized value, they don't differ from one another.
B) These groups are not significantly different from one another.
C) These groups are significantly different from one another.
D) We lack good evidence to decide whether these groups are significantly different from one another or not.

Question 30

Imagine a series of turbidity (cloudiness) measurements in the water from two different lakes. The measurements were taken over many different days (30 samples for each lake) and the figure shows the mean turbidity of those measurements along with bars representing 95% confidence intervals. What can we conclude about the appropriate null hypothesis and mean turbidity of the two lakes?
​
​

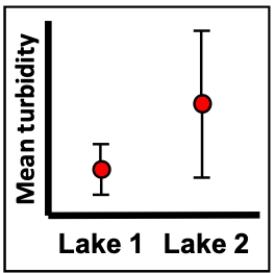
A) Fail to reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
B) Reject the null hypothesis, we have evidence that the turbidity differs between the lakes.
C) Reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
D) We can't really tell from this figure whether the null hypothesis will be rejected or not.

Question 31

Imagine a series of turbidity (cloudiness) measurements in the water from two different lakes. The measurements were taken over many different days (30 samples for each lake) and the figure shows the mean turbidity of those measurements along with bars representing 95% confidence intervals. What can we conclude about the appropriate null hypothesis and mean turbidity of the two lakes?
​
​

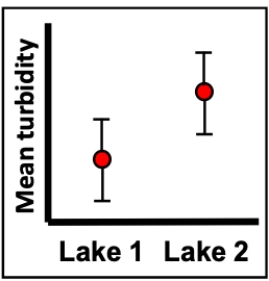
A) Fail to reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
B) Reject the null hypothesis, we have evidence that the turbidity differs between the lakes.
C) Reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
D) We can't really tell from this figure whether the null hypothesis will be rejected or not.

Question 32

Imagine a series of turbidity (cloudiness) measurements in the water from two different lakes. The measurements were taken over many different days (30 samples for each lake) and the figure shows the mean turbidity of those measurements along with bars representing 95% confidence intervals. What can we conclude about the appropriate null hypothesis and mean turbidity of the two lakes?
​
​

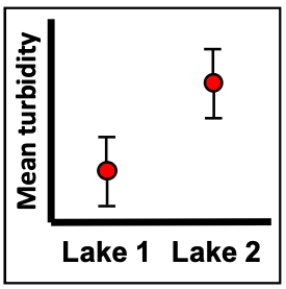
A) Fail to reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
B) Reject the null hypothesis, we have evidence that the turbidity differs between the lakes.
C) Reject the null hypothesis, we lack evidence that the turbidity differs between the lakes.
D) We can't really tell from this figure whether the null hypothesis will be rejected or not.

Question 33

The F-test for comparing variances has a stringent assumption that is often not met in data sets we are analyzing. What is it?

A) The data distributions must have equal means.
B) The data distributions must have equal variances.
C) The data must be binomially distributed.
D) The data must be normally distributed.

Question 34

Which of the following is not an advantage of Levene's test versus the F-test as a test of population variances?

A) It can compare more than two groups.
B) It is more robust to deviations from normality in the data distributions.
C) It is more robust to deviations from symmetry in the data distributions.
D) It uses the normal distribution instead of the F distribution.

Question 35

In a paired design, both treatments are applied to every sampled unit.

Question 36

In a paired design, numerical values from each treatment are compared with the numerical values from the other treatment that are most similar.

Question 37

The paired t-test is essentially the same as a one-sample t-test of the set of differences with a hypothesized mean of zero for the differences.

Question 38

The paired t-test can be used even in some cases in which the population values are highly non-normal.

Question 39

The pooled sample variance is the mean of the variances, weighted by their degrees of freedom.

Question 40

If the 95% confidence interval for the difference between the means includes the value zero, then we are likely to get a P-value less than 0.05 when we do a two-sample t-test.

Question 41

Welch's t-test may only be used when the population variances are equal.

Question 42

If the mean of population A is significantly different from 20, but the mean of group B is not significantly different from 20, then the mean of the two population are different from one another.

Question 43

If the means of two populations are both significantly different from the same value, then they are significantly different from one another.

Question 44

When a figure shows means and bars showing the 95% confidence interval, and the range defined by the bars in one group overlaps the mean of the other, then the results of a t-test would always fail to reject the null hypothesis that the means are equal.

Question 45

When a figure shows means and bars indicating one standard error above and below each mean, and the range defined by the bars in one group overlaps the mean of the other, then the results of a t-test would always fail to reject the null hypothesis that the means are equal.

Question 46

When a figure shows means and bars indicating one standard deviation above and below each mean, and the range defined by the bars in one group overlaps the mean of the other, then the results of a t-test would always fail to reject the null hypothesis that the means are equal.

Question 47

Describe a study to measure a physiological variable using twins that would be appropriate for a paired t-test and another design of the experiment, also using twins, that would not be appropriate for analyzing with a paired t-test.

Question 48

Draw a flowchart to describe the steps you would take when presented with data from two different groups, and the goal is to identify if the means of the groups differ. You may assume the data values are normally distributed. Include each possible statistical test.

Question 49

Consider a study in which two sets of 20 mice were given different amounts of caffeine in their drinking water. Members of the control group got none and members of the experimental group received 0.01% caffeine in their water. The number of minutes each mouse spent running on the wheel in their cage was measured over a series of 14 nights.
Describe why the appropriate sampling unit is the mean number of minutes for each of the 40 mice rather than the number of minutes during each of the 280 nights.
What are the sample sizes you would use when comparing this running data in the two groups?

Question 50

Consider a study in which two sets of 20 mice were given different amounts of caffeine in their drinking water. Members of the control group got none and members of the experimental group received 0.01% caffeine in their water. Their activity levels were measured using the mean number of minutes each mouse spent running on the wheel in their cage over a series of 14 nights.
Control treatment: mean = 305 minutes, standard deviation = 50 minutes
Caffeine treatment: mean = 340 minutes, standard deviation = 60 minutes
You may assume that the variances are equal for the purposes of conducting a two-sample t-test.
Perform a complete two-sample t-test. Summarize your results with a statement about the 95% confidence interval for the difference between the means, draw a figure showing the 95 confidence intervals for each treatment, present the t-test statistic and P-value for the two-sample test, and state your conclusion with regard to accepting or rejecting the null hypothesis and what this means for the effects of caffeine on mouse activity levels.

Question 51

Consider a study in which two sets of 20 mice were given different amounts of caffeine in their drinking water. Members of the control group got none and members of the experimental group received 0.01% caffeine in their water. Their activity levels were measured using the mean number of minutes each mouse spent running on the wheel in their cage over a series of 14 nights.
Control treatment: mean = 305 minutes, standard deviation = 40 minutes
Caffeine treatment: mean = 340 minutes, standard deviation = 50 minutes
You may assume that the variances are equal for the purposes of conducting a two-sample t-test.
Perform a complete two-sample t-test. Summarize your results with a statement about the 95% confidence interval for the difference between the means, draw a figure showing the 95% confidence intervals for each treatment, present the t-test statistic and P-value for the two-sample test, and state your conclusion with regard to accepting or rejecting the null hypothesis and what this means for the effects of caffeine on mouse activity levels.

Question 52

Consider a study in which two sets of 20 mice were given different amounts of caffeine in their drinking water. Members of the control group got none and members of the experimental group received 0.01% caffeine in their water. Their activity levels were measured using the mean number of minutes each mouse spent running on the wheel in their cage over a series of 14 nights.
Control treatment: mean = 305 minutes, standard deviation = 40 minutes
Caffeine treatment: mean = 340 minutes, standard deviation = 70 minutes
Because the variances may be different, use the Welch's t-test approach for this data.
Perform a complete two-sample t-test. Summarize your results with a statement about the 95% confidence interval for the difference between the means, draw a figure showing the 95% confidence intervals for each treatment, present the t-test statistic and P-value for the two-sample test, and state your conclusion with regard to accepting or rejecting the null hypothesis and what this means for the effects of caffeine on mouse activity levels.

Question 53

Consider a study in which two sets of 20 mice were given different amounts of caffeine in their drinking water. Members of the control group got none and members of the experimental group received 0.01% caffeine in their water. Their activity levels were measured using the mean number of minutes each mouse spent running on the wheel in their cage over a series of 14 nights.
Control treatment: mean = 305 minutes, standard deviation = 30 minutes
Caffeine treatment: mean = 340 minutes, standard deviation = 60 minutes.
Because the variances may be different, use the Welch's t-test approach for this data
Perform a complete two-sample t-test. Summarize your results with a statement about the 95% confidence interval for the difference between the means, draw a figure showing the 95% confidence intervals for each treatment, present the t-test statistic and P-value for the two-sample test, and state your conclusion with regard to accepting or rejecting the null hypothesis and what this means for the effects of caffeine on mouse activity levels.