Deck 11: Factorial Anova

Question 1

How many independent variables and how many cells, respectively, exist in a 3 x 4 x 5 between-between-within design?

A) 2, 12
B) 2, 60
C) 3, 35
D) 3, 60

Answer 1

D

Question 2

What concept is strengthened when no significant interactions are found?

A) Generalizability
B) Statistical importance
C) Reliability
D) Validity

Answer 2

A

Question 3

How many subjects would the researcher need to recruit for a 2 x 3 between-between two-way ANOVA if five subjects received each possible treatment combination?

A) 5
B) 10
C) 15
D) 30

Answer 3

D

Question 4

In a two-way ANOVA where both independent variables are between factors, how many parts is the sum of squares total partitioned into, and how many of them are part of the explained variance, respectively?

A) 3, 1
B) 3, 3
C) 4, 3
D) 4, 4

Question 5

What is an alternative term for a between-within two-way ANOVA?

A) A biased model
B) A fixed model
C) A mixed model
D) A random model

Question 6

The VO₂max of 10 males and 10 females was measured before and after a 12-week physical fitness program. What type of design would be appropriate for analyzing the resulting data?

A) 2 x 2, mixed
B) 2 x 2, within-within
C) 2 x 2 x 1, fixed
D) 2 x 2 x 1, between-between-within

Question 7

The VO₂max of 10 males and 10 females was measured before and after a 12-week physical fitness program. How many subjects would be required to execute this study, and how many F-ratios would be calculated?

A) 20, 1
B) 20, 3
C) 40, 1
D) 40, 3

Question 8

The VO₂max of 10 males and 10 females was measured before and after a 12-week physical fitness program. What are the independent and dependent variables in this study?

A) (Independent) VO₂max (Dependent) Gender, Training
B) (Independent) Time (Dependent) VO₂max
C) (Independent) Training, Gender (Dependent) Time
D) (Independent) Gender, Time (Dependent) VO₂max

Question 9

The VO₂max of 10 males and 10 females was measured before and after a 12-week physical fitness program. How many degrees of freedom would be associated with the numerator of the F-ratio for interaction?

A) 1
B) 2
C) 4
D) 8

Question 10

In a 2 x 4 within-within design, there are 10 subjects in the cell where the first levels of each independent variable intersect. What is the total number of subjects needed to carry out this experiment?

A) 8
B) 10
C) 40
D) 80

Question 11

How many main effects exist in a 2 x 3 x 2 design?

A) 3
B) 4
C) 7
D) 12

Question 12

Which of the following does not belong with the others?

A) A dependent t-test
B) A repeated-measures ANOVA
C) A within-within design
D) A 2 x 3 design with different subjects in every cell

Question 13

In a 3 x 5 between-between design, what are the degrees of freedom for the numerators of the three F-ratios?

A) 2, 4, 8
B) 3, 4, 12
C) 2, 4, 15
D) 3, 5, 15

Question 14

What is the most important reason for using a 2 x 2 factorial design instead of two separate experiments with one independent variable in each?

A) To test for main effects
B) To test for interaction
C) To use resources effectively
D) There is no good reason; separate experiments would be preferred.

Question 15

What is the only way to determine whether an interaction exists between independent variables?

A) Include both of them in the design
B) Add a third level of an independent variable
C) Add more subjects to the experiment
D) Add a control variable to the experiment

Question 16

If a researcher states, "Heavy drinking leads to decreased GPA, regardless of the student's intelligence level," what was found?

A) A main effect for drinking
B) A main effect for intelligence
C) An interaction between drinking and GPA
D) All of the above

Question 17

How many interactions are examined in a 3 x 3 between-groups design?

A) 9
B) 6
C) 3
D) 1

Question 18

What has the researcher determined when an experiment reveals that strength training is effective for building muscle mass only when paired with a high-protein diet?

A) A training by diet interaction
B) A main effect for diet
C) A main effect for training
D) No main effects

Question 19

Factorial experimental designs must have which of the following?

A) One control variable
B) More than two dependent variables
C) An independent variable with at least three levels
D) Two or more independent variables

Question 20

Which design can be used to test for the existence of interactions?

A) A multiple dependent variable design
B) A multiple confounding variable design
C) A multiple independent variable design
D) All of the above

Question 21

How many interactions are available for testing in a 3 x 3 x 3 design?

A) 3
B) 4
C) 6
D) It depends on whether variables are fixed or random

Question 22

Which of the following describes an interaction between independent variables?

A) When one independent variable causes a change in the dependent variable
B) When both independent variables cause a change in the dependent variable
C) When the effect of one independent variable on the dependent variable depends on the level of the other independent variable
D) When a confounding variable is present

Question 23

What results are evaluated when an experiment has two independent variables?

A) One interaction
B) One main effect and one interaction
C) Two main effects and one interaction
D) Two main effects and two interactions

Question 24

You have designed an experiment with three independent variables: mode of presentation (visual, auditory); difficulty level (easy, difficult); and amount of information (minimal, moderate, maximum). Which of the following describes the design of the study?

A) 2 x 2
B) 2 x 3
C) 2 x 2 x 2
D) 2 x 2 x 3

Question 25

You have designed an experiment with three independent variables: mode of presentation (visual, auditory); difficulty level (easy, difficult); and amount of information (minimal, moderate, maximum). How many main effects would be tested?

A) 1
B) 2
C) 3
D) 12

Question 26

You have designed an experiment with three independent variables: mode of presentation (visual, auditory); difficulty level (easy, difficult); and amount of information (minimal, moderate, maximum). How many interactions would be tested?

A) 1
B) 2
C) 3
D) 4

Question 27

You have designed an experiment with three independent variables: mode of presentation (visual, auditory); difficulty level (easy, difficult); and amount of information (minimal, moderate, maximum). How many subjects are needed, if the three independent variables are between factors, with 10 subjects in each condition?

A) 10
B) 60
C) 70
D) 120

Question 28

An analysis of GPA by class standing (FR, SO, JR, SR) and major (Social Science [SS] or Natural Science [NS]) revealed the following mean values:
Which of the following conclusions would be most likely?
$\begin{array}{|l|l|l|l|l|}\hline & \mathrm{FR} & \mathrm{SO} & \mathrm{JR} & \mathrm{SR} \\\hline \mathrm{SS} & 2.7 & 2.8 & 3.1 & 3.2 \\\hline \mathrm{NS} & 2.6 & 2.8 & 3.0 & 3.2 \\\hline\end{array}$

A) Significant main effect for class standing
B) Significant main effect for major
C) Significant class standing by major interaction
D) None of the above

Question 29

A three-way ANOVA is useful in determining the relationship between what variables?

A) An independent variable and a dependent variable
B) Two independent variables and a dependent variable
C) Two independent variables and two dependent variables
D) Three independent variables and a dependent variable

Question 30

An experiment involves determining the effect of three methods of presenting physical activity (swimming, jogging, and bicycling) and the effect of two altitudes (chosen at random to be 906 feet and 1298 feet above sea level) on a measure of physical fitness. What statistical design should be used to analyze these data?

A) One-way fixed-factor ANOVA
B) One-way random-factor ANOVA
C) Two-way mixed-factors ANOVA
D) Two-way fixed-factors ANOVA

Question 31

What is the total number of measurements taken for a 3 x 2 factorial experiment, if both independent variables are within factors and there are 20 subjects?

A) 6
B) 60
C) 120
D) 240

Question 32

The following values are known for a two-way ANOVA: SS_T = 1000, SS_Explained = 800, SS_A = 400, and SS_B = 300. What are the values for SS_AB and SS_W?

A) (SS_AB)300 (SS_W)200
B) (SS_AB)200 (SS_W)300
C) (SS_AB)100 (SS_W)300
D) (SS_AB)100 (SS_W)200

Question 33

If the degrees of freedom in a two-way ANOVA for MS_A, MS_B, MS_AB, and MS_W are 4, 7, 28, and 200, respectively, how many treatments exist in factor A and factor B, and how many subjects are in each cell of the design?

A) 3, 6, 12 (Factor A, Factor B, Subjects/cell, respectively)
B) 4, 7, 5 (Factor A, Factor B, Subjects/cell, respectively)
C) 5, 8, 6 (Factor A, Factor B, Subjects/cell, respectively)
D) 5, 8, 4(Factor A, Factor B, Subjects/cell, respectively)

Question 34

Using the following summary of results, how many levels exist in factors A and B, respectively? (Assume a between-groups, fixed-factors model.) $\begin{array}{lcccc} \text { Source of } &\text { SS } & d f & \text { MS } & \text { F } \\ \text { Variation } && & & \\ \text { Factor A } &500 & 2 & \mathrm{H} & \mathrm{J} \\ \text { Factor B } &\text { C } & 3 & 200 & \mathrm{~K} \\ \text { AB Interaction } &\text { 900 } & \text { F } & 1 & \mathrm{~L} \\ \text { Within } &\text { D } & 60 & 50 & \\ \text { Total } &\text { E } & \text { G } & &\end{array}$

A) 2,3
B) 3,3
C) 3,4
D) 4,4

Question 35

Using the following summary of results, what F-ratios, if any, are significant at the .05 alpha level? (Assume a between-groups, fixed-factors model.) $\begin{array}{lcccc} \text {Source of } &\text { SS } & d f & \text { MS } & \text { F } \\ \text { Variation } && & & \\ \text { Factor A } &500 & 2 & \text { H } & \text { J } \\ \text { Factor B } &\text { C } & 3 & 200 & \mathrm{~K} \\ \text { AB Interaction } &900 & \text { F } & 1 & \text { L } \\ \text { Within } &\text { D } & 60 & 50 & \\ \text { Total } &\text { E } & \text { G } & &\end{array}$

A) Factor A
B) Factor B
C) AB interaction
D) Factor, A, Factor B, AB interaction
E) None are significant

Question 36

For the following data, assume a significant F-ratio was found for factor A. What further test, if any, would be appropriate? $\begin{array}{c} \quad \quad \quad \quad \quad \quad \quad \quad\text { Factor B }\\\text { Factor A }\begin{array}{lll}& \text {Level 1}& \text {Level 2}& \text {Level 2}\\ \text {Level 1}&n=12 & n=15 &n=21 \\ \text {Level 2 }& n=18 & n=10 & n=14 \\\end{array}\end{array}$

A) Tukey test
B) Scheffé test
C) Either Tukey or Scheffé test
D) Neither Tukey nor Scheffé test

Question 37

Which of the following is least likely to be a random independent variable?

A) Sex
B) Rater
C) Person
D) Teacher

Question 38

An ANOVA is designed to assess the effects of gender, three classifications of social-economic status, and two teaching methods on the learning of statistical concepts. Which design is appropriate?

A) 1 x 3 x 2
B) 2 x 3 x 2
C) 2 x 3 x 2 x 1
D) 1 x 3 x 2 x 1

Question 39

To what does the term factorial ANOVA refer?

A) The number of independent variables
B) The number of dependent variables
C) Both the numbers of independent and dependent variables
D) It depends on whether the model is between-groups or within-groups.

Question 40

Many junior high school students drink colas on a daily basis. A researcher is interested in testing the effects of cola ingestion on academic performance (AP) for girls in the ninth grade. One thousand ninth-grade girls are the subjects. They are grouped according to the number of colas they drink each day (low, medium, and high). The researcher concluded that cola ingestion had an effect on academic performance. What are the independent variable (IV) and dependent variable (DV) in this study?

A) (IV) ninth grade (DV) AP
B) (IV) AP (DV) cola
C) (IV) cola (DV) gender
D) (IV) cola (DV) AP
E) (IV) gender (DV) cola

Question 41

Many junior high school students drink colas on a daily basis. A researcher is interested in testing the effects of cola ingestion on academic performance (AP) for girls in the ninth grade. One thousand ninth-grade girls are the subjects. They are grouped according to the number of colas they drink each day (low, medium, and high). The researcher concluded that cola ingestion had an effect on academic performance. What statistical procedure did the researchers probably use?

A) z-test
B) Independent groups t-test
C) Paired t-test
D) ANOVA

Question 42

Many junior high school students drink colas on a daily basis. A researcher is interested in testing the effects of cola ingestion on academic performance (AP) for girls in the ninth grade. One thousand ninth-grade girls are the subjects. They are grouped according to the number of colas they drink each day (low, medium, and high). The researcher concluded that cola ingestion had an effect on academic performance. What did the researchers do with the null hypothesis?

A) Rejected it
B) Determined it was still tenable
C) Impossible to determine without knowing the α level

Question 43

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

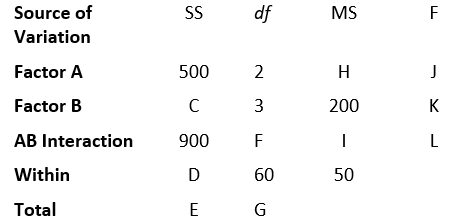
-C_____

Question 44

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-D_____

Question 45

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-E_____

Question 46

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-F_____

Question 47

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-G_____

Question 48

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-H_____

Question 49

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-I_____

Question 50

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-J_____

Question 51

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-K_____

Question 52

Using the following summary of results, what are the values that have been replaced by letters? (Assume a between-groups, fixed-factors model.)

-L_____