Deck 10: Factorial Analysis of Variance

Question 1

Suppose I wanted to know something about how much teachers are paid. I think there may be differences in pay by gender and by school level (elementary, middle, high school). I select random samples of 30 male and 30 female teachers at each of these three school levels.
a. What are my dependent and independent variables?

Answer 1

Dependent: Amount of annual pay.
Independent: Gender and school level.

Question 2

Here is the average annual pay of teachers in each of my groups.
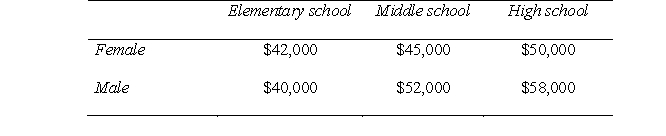a. Create a column graph that represents these data accurately.
b. Looking at the data in the table and the column graph, do you think there is a main effect for gender?
c. Looking at the data in the table and the column graph, do you think there is a main effect for school level?
d. Looking at the data in the table and the column graph, do you think there is an interaction effect for gender X school level?
e. What is the argument against interpreting main effect when there is a statistically significant interaction effect?
f. Suppose that for the main effect of school level F_{(2, 174)} = 5.49. Is this a statistically significant main effect?
g. "Wait a second!" someone says. "Those differences between groups may be caused by how long the teachers have been on the job. Everyone knows that the more experienced teachers get paid more. You have to control for that!" So I add "Years of teaching experience" to the model to control for its effects on teacher pay. What is this kind of variable called?

Answer 2

a.

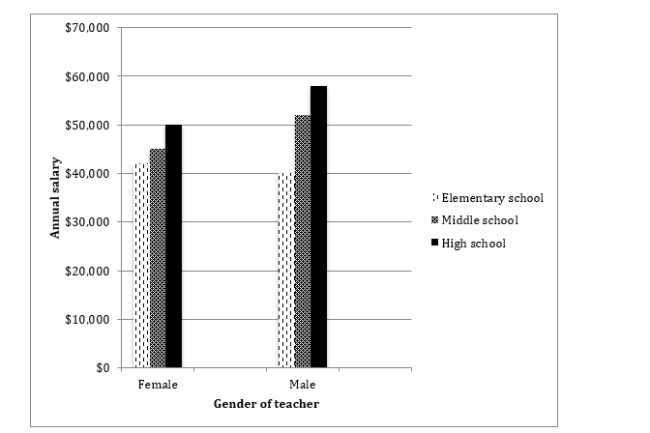
b. It does appear that there is a main effect for gender. Although female teachers are paid slightly more than male teachers in elementary school, male teachers are paid substantially more than females at the other two grade levels. Overall, across all three grade levels combined, it appears that male teachers are paid more than female teachers, on average. We would need to calculate the F value to know for sure.
c. I think so. For each gender, it appears that at the older levels of schooling (i.e., high school compared to middle school and middle school compared to high school), teachers are paid more. We would need to calculate the F value to determine whether this difference is statistically significant.
d. It looks like there may be. Whereas male teachers earn slightly less than female teachers at the elementary school level, the reverse is true in middle and high school levels, and the gap between the genders widens. We would need to calculate the F value to determine whether this interaction effect is statistically significant.
e. A significant interaction effect qualifies, or puts conditions upon, the main effects. In the current example, we may see a main effect for gender, indicating that male teachers earn more than female teachers. But notice that this is not true at the elementary school level, because of the presence of the interaction effect. The interaction would make our statement about gender differences true only for some levels of schooling, not for all. So it can be somewhat misleading to say there is a main effect when there is also a significant interaction effect.
f. With an alpha level of .05 and 2 and 150 degrees of freedom (150 df_e is the closest we can get to our actual df_e of 174 in Appendix C), we find a critical F value in Appendix C of 3.06. Because this critical F value is well below our observed F value of 5.49, the main effect of school level would be considered statistically significant.
g. A covariate.