Deck 6: Eigenvalues and Eigenvectors
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/75
Play
Full screen (f)
Deck 6: Eigenvalues and Eigenvectors
1
Determine which of 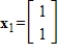 ,
, 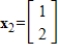 , and
, and 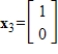 are eigenvectors of
are eigenvectors of 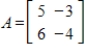 , and determine the associated eigenvalues.
, and determine the associated eigenvalues.
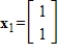 ,
, 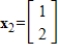 , and
, and 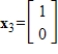 are eigenvectors of
are eigenvectors of 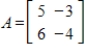 , and determine the associated eigenvalues.
, and determine the associated eigenvalues. is an eigenvector with eigenvalue 2,
is an eigenvector with eigenvalue 2, 
is an eigenvector with eigenvalue
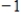
.
2
Determine which of 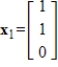 ,
, 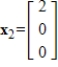 , and
, and 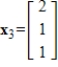 are eigenvectors of
are eigenvectors of 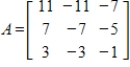
,
and determine the associated eigenvalues.
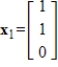 ,
, 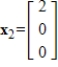 , and
, and 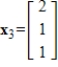 are eigenvectors of
are eigenvectors of 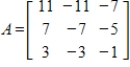
,
and determine the associated eigenvalues.
 is an eigenvector with eigenvalue 0,
is an eigenvector with eigenvalue 0, 
is an eigenvector with eigenvalue 2.
3
Find a basis for the eigenspace associated with eigenvalue 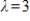 for matrix
for matrix 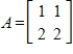
.
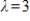 for matrix
for matrix 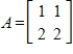
.
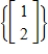
4
Find a basis for the eigenspace associated with eigenvalue 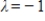 for matrix
for matrix 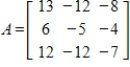
.
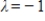 for matrix
for matrix 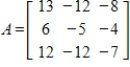
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
5
Find a basis for the eigenspace associated with eigenvalue 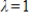 for the matrix
for the matrix
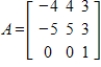
.
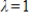 for the matrix
for the matrix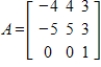
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
6
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 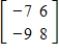
.
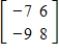
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
7
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 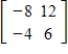
.
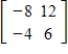
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
8
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 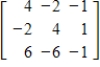
.
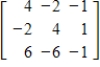
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
9
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 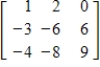
.
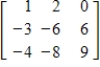
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
10
Find the characteristic polynomial, the eigenvalues, and a basis for each eigenspace for the matrix A = 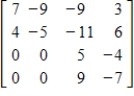
.
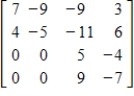
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
11
An 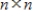 matrix A can have no more than n eigenvalues.
matrix A can have no more than n eigenvalues.
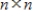 matrix A can have no more than n eigenvalues.
matrix A can have no more than n eigenvalues.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
12
If 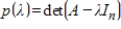 is the characteristic polynomial of an
is the characteristic polynomial of an 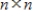 matrix A, and
matrix A, and 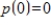 , then A is not invertible.
, then A is not invertible.
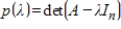 is the characteristic polynomial of an
is the characteristic polynomial of an 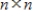 matrix A, and
matrix A, and 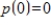 , then A is not invertible.
, then A is not invertible.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose the 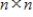 matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
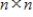 matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
matrix A has n distinct eigenvalues. Then the dimension of each eigenspace is 1.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
14
If u and v are both eigenvectors of an n ×n matrix A, then u+v is also an eigenvector of the A.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
15
If 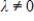 is an eigenvalue of an invertible
is an eigenvalue of an invertible 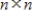 matrix A, then
matrix A, then 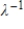 is an eigenvalue of the matrix
is an eigenvalue of the matrix 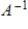
.
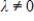 is an eigenvalue of an invertible
is an eigenvalue of an invertible 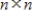 matrix A, then
matrix A, then 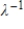 is an eigenvalue of the matrix
is an eigenvalue of the matrix 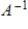
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
16
Compute 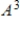 if
if 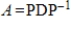
.
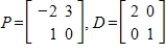
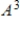 if
if 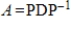
.
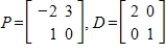

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
17
Compute 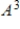 if
if 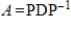
.
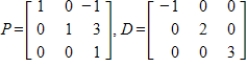
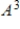 if
if 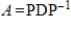
.
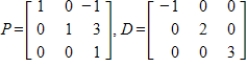

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
18
Find the matrix A that has the given eigenvalues and corresponding eigenvectors.
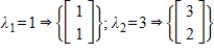
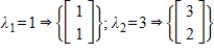

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
19
Find the matrix A that has the given eigenvalues and bases for the corresponding eigenspaces.
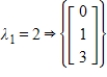
;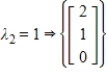
;

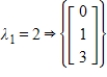
;
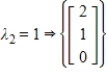
;


Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
20
Find the matrix A that has the given eigenvalues and bases for the corresponding eigenspaces.
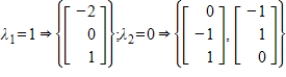
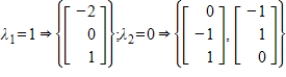

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
21
Diagonalize the matrix A, if possible.
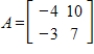
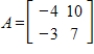

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
22
Diagonalize the matrix A, if possible.
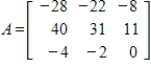
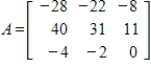

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
23
Diagonalize the matrix A, if possible.
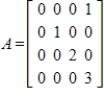
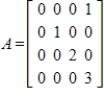

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
24
Diagonalize the given matrix A, and use the diagonalization to compute 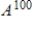
.
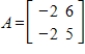
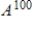
.
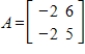

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
25
Diagonalize the given matrix A, and use the diagonalization to compute 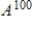
.

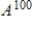
.


Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
26
If an 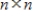 matrix A has n distinct eigenvalues, then A is diagonalizable.
matrix A has n distinct eigenvalues, then A is diagonalizable.
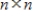 matrix A has n distinct eigenvalues, then A is diagonalizable.
matrix A has n distinct eigenvalues, then A is diagonalizable.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
27
The matrix 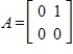 is diagonalizable.
is diagonalizable.
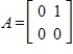 is diagonalizable.
is diagonalizable.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
28
If A and  are
are  diagonalizable matrices, then AB is diagonalizable.
diagonalizable matrices, then AB is diagonalizable.
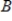 are
are 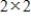 diagonalizable matrices, then AB is diagonalizable.
diagonalizable matrices, then AB is diagonalizable.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
29
If 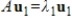 and
and 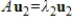 , where
, where 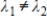 , and
, and 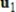 and
and  are nonzero vectors, then
are nonzero vectors, then 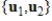 is linearly independent.
is linearly independent.
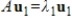 and
and 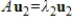 , where
, where 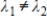 , and
, and 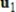 and
and  are nonzero vectors, then
are nonzero vectors, then 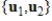 is linearly independent.
is linearly independent.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
30
If A is diagonalizable, then 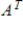 is diagonalizable.
is diagonalizable.
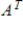 is diagonalizable.
is diagonalizable.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
31
Find the eigenvalues and a basis for each eigenspace for the given matrix.
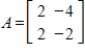
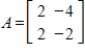

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
32
Find the eigenvalues and a basis for each eigenspace for the given matrix.
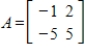
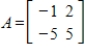

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
33
Find the eigenvalues and a basis for each eigenspace for the given matrix.
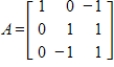
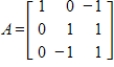

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
34
Find the eigenvalues and a basis for each eigenspace for the given matrix.
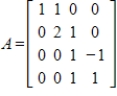
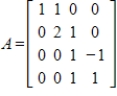

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
35
Determine the rotation and dilation that result from multiplying vectors in  by the given matrix.
by the given matrix.
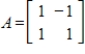
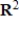 by the given matrix.
by the given matrix.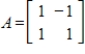

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
36
Determine the rotation and dilation that result from multiplying vectors in 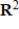 by the given matrix.
by the given matrix.
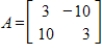
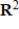 by the given matrix.
by the given matrix.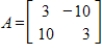

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
37
Find the rotation-dilation matrix B within the given matrix A. 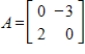
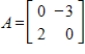

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
38
Find the rotation-dilation matrix B within the given matrix A. 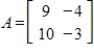
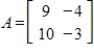

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
39
Factor the matrix 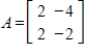 from Question 1 in the form
from Question 1 in the form 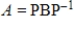 where B is a rotation-dilation matrix.
where B is a rotation-dilation matrix.
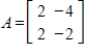 from Question 1 in the form
from Question 1 in the form 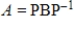 where B is a rotation-dilation matrix.
where B is a rotation-dilation matrix.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
40
Factor the matrix 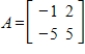 from Question 2 in the form
from Question 2 in the form 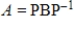 where B is a rotation-dilation matrix.
where B is a rotation-dilation matrix.
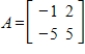 from Question 2 in the form
from Question 2 in the form 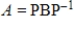 where B is a rotation-dilation matrix.
where B is a rotation-dilation matrix.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
41
Factor the given matrix A in the form 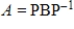 where B is a rotation-dilation matrix. Find the dilation and angle of rotation. Use this information to evaluate the matrix power
where B is a rotation-dilation matrix. Find the dilation and angle of rotation. Use this information to evaluate the matrix power 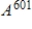 without computing it directly.
without computing it directly.
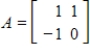
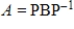 where B is a rotation-dilation matrix. Find the dilation and angle of rotation. Use this information to evaluate the matrix power
where B is a rotation-dilation matrix. Find the dilation and angle of rotation. Use this information to evaluate the matrix power 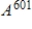 without computing it directly.
without computing it directly.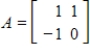

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
42
If A is a real matrix, and 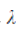 is a complex eigenvalue of A, then
is a complex eigenvalue of A, then 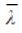 is also an eigenvalue of A.
is also an eigenvalue of A.
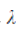 is a complex eigenvalue of A, then
is a complex eigenvalue of A, then 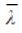 is also an eigenvalue of A.
is also an eigenvalue of A.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
43
If A is a real matrix and 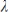 is an eigenvalue of A with
is an eigenvalue of A with 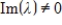 and corresponding eigenvector u, then
and corresponding eigenvector u, then 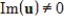
.
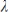 is an eigenvalue of A with
is an eigenvalue of A with 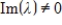 and corresponding eigenvector u, then
and corresponding eigenvector u, then 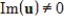
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
44
If the 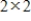 invertible matrix A has hidden rotation-dilation matrix
invertible matrix A has hidden rotation-dilation matrix 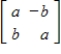 , where
, where 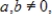 then
then 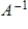 has hidden rotation-dilation matrix
has hidden rotation-dilation matrix 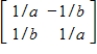
.
 invertible matrix A has hidden rotation-dilation matrix
invertible matrix A has hidden rotation-dilation matrix 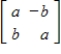 , where
, where 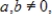 then
then 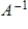 has hidden rotation-dilation matrix
has hidden rotation-dilation matrix 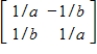
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
45
If 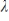 is an eigenvalue of the real
is an eigenvalue of the real 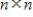 matrix A with corresponding eigenvector
matrix A with corresponding eigenvector  , then
, then 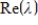 is an eigenvalue of
is an eigenvalue of 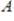 with corresponding eigenvector
with corresponding eigenvector 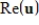
.
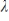 is an eigenvalue of the real
is an eigenvalue of the real 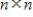 matrix A with corresponding eigenvector
matrix A with corresponding eigenvector  , then
, then 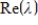 is an eigenvalue of
is an eigenvalue of 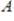 with corresponding eigenvector
with corresponding eigenvector 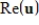
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
46
The coefficient matrix for a system of linear differential equations of the form 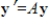 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
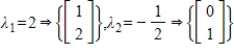
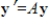 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.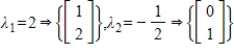

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
47
The coefficient matrix for a system of linear differential equations of the form 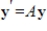 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
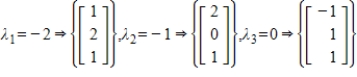
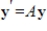 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.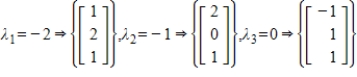

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
48
The coefficient matrix for a system of linear differential equations of the form 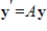 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
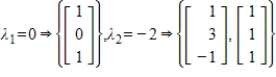
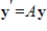 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.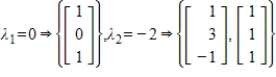

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
49
The coefficient matrix for a system of linear differential equations of the form 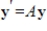 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
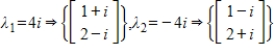
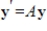 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.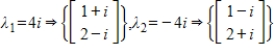

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
50
The coefficient matrix for a system of linear differential equations of the form 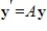 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
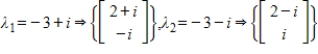
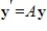 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.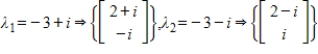

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
51
The coefficient matrix for a system of linear differential equations of the form 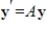 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.
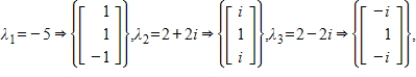
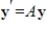 has the given eigenvalues and eigenspace bases. Find the general solution for the system.
has the given eigenvalues and eigenspace bases. Find the general solution for the system.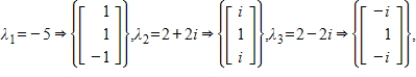

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
52
Find the general solution for the system 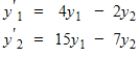
.
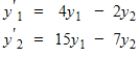
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
53
Find the general solution for the system 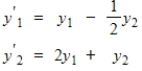
.
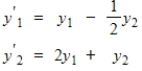
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
54
Find the solution for the system that satisfies the condition at t = 0.
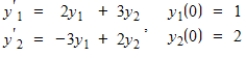
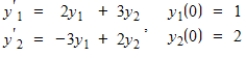

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
55
Find the solution for the system that satisfies the condition at t = 0.
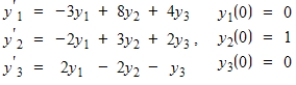
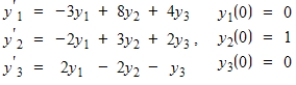

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose that two countries are in an arms race modeled by the system of differential equations
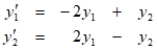
where y1 and y2 are measured in thousands. Find the solution for the system with initial conditions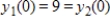 , and use it to predict the long-term amounts of arms held by each country.
, and use it to predict the long-term amounts of arms held by each country.
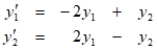
where y1 and y2 are measured in thousands. Find the solution for the system with initial conditions
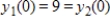 , and use it to predict the long-term amounts of arms held by each country.
, and use it to predict the long-term amounts of arms held by each country.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
57
If 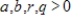 , and
, and  are solutions to the initial-value problem
are solutions to the initial-value problem 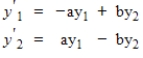 , with
, with 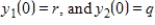 , then
, then 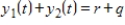 for all t.
for all t.
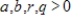 , and
, and  are solutions to the initial-value problem
are solutions to the initial-value problem 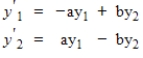 , with
, with 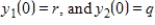 , then
, then 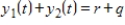 for all t.
for all t.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
58
If A is a real square matrix with complex eigenvalue 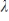 and associated eigenvector
and associated eigenvector  , then
, then 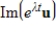 is a real solution to the system
is a real solution to the system 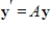
.
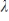 and associated eigenvector
and associated eigenvector  , then
, then 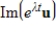 is a real solution to the system
is a real solution to the system 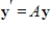
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose that A is an 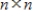 matrix and
matrix and 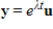 is a solution to the system of linear differential equations
is a solution to the system of linear differential equations 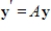 where
where  is an eigenvector of A with associated eigenvalue
is an eigenvector of A with associated eigenvalue 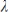
. Let k be any scalar. Then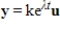 is a solution to the system
is a solution to the system 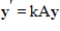
.
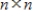 matrix and
matrix and 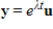 is a solution to the system of linear differential equations
is a solution to the system of linear differential equations 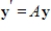 where
where  is an eigenvector of A with associated eigenvalue
is an eigenvector of A with associated eigenvalue 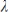
. Let k be any scalar. Then
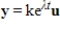 is a solution to the system
is a solution to the system 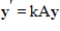
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose that A is an 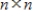 matrix and
matrix and 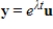 is a solution to the system of linear differential equations
is a solution to the system of linear differential equations 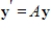 where
where  is an eigenvector of A with associated eigenvalue
is an eigenvector of A with associated eigenvalue 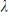
. If A is invertible, then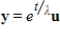 is a solution to the system
is a solution to the system 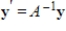
.
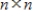 matrix and
matrix and 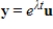 is a solution to the system of linear differential equations
is a solution to the system of linear differential equations 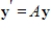 where
where  is an eigenvector of A with associated eigenvalue
is an eigenvector of A with associated eigenvalue 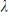
. If A is invertible, then
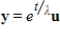 is a solution to the system
is a solution to the system 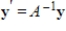
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
61
Compute the first three iterations of the Power Method without scaling, starting with the given 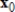 , where
, where 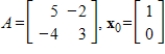
.
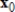 , where
, where 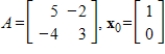
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
62
Compute the first three iterations of the Power Method without scaling, starting with the given 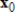 , where
, where 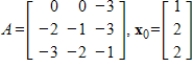
.
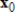 , where
, where 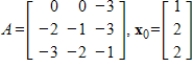
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
63
Compute the first two iterations of the Power Method with scaling, starting with the given 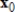 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
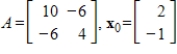
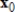 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.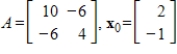

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
64
Compute the first two iterations of the Power Method with scaling, starting with the given 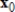 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
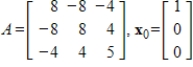
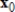 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.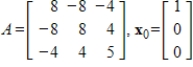

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
65
Compute the first two iterations of the Inverse Power Method, starting with the given 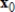 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
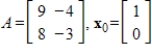
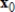 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.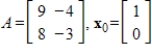

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
66
Compute the first two iterations of the Shifted Inverse Power Method, starting with the given 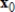 , to determine the eigenvalue of A closest to
, to determine the eigenvalue of A closest to 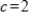 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
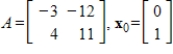
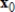 , to determine the eigenvalue of A closest to
, to determine the eigenvalue of A closest to 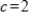 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.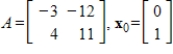

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
67
The dominant eigenvalue of the matrix A given below is 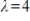
. Compute the first two iterations of the Shifted Power Method with scaling, starting with the given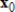 , to determine the eigenvalue farthest from
, to determine the eigenvalue farthest from 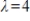 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.
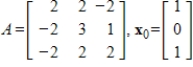
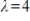
. Compute the first two iterations of the Shifted Power Method with scaling, starting with the given
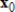 , to determine the eigenvalue farthest from
, to determine the eigenvalue farthest from 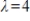 , rounding any numerical values to two decimal places.
, rounding any numerical values to two decimal places.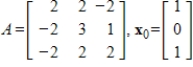

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
68
Use the Power Method with scaling to determine an eigenvalue and associated eigenvector of A, starting with the given 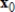
.
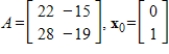
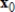
.
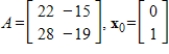

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
69
Use the Power Method with scaling to determine an eigenvalue and associated eigenvector of A, starting with the given 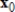
.
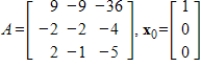
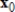
.
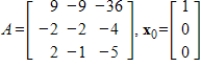

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
70
Use the Power Method with scaling to determine an eigenvalue and associated eigenvector of A, starting with the given 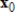
.
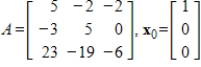
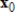
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
71
The Power Method applied to the matrix 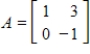 and vector
and vector 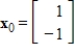 converges.
converges.
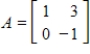 and vector
and vector 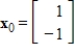 converges.
converges.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
72
The Power Method applied to the matrix 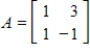 and vector
and vector 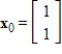 converges.
converges.
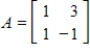 and vector
and vector 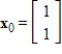 converges.
converges.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
73
The Inverse Power Method applied to the matrix 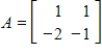 and vector
and vector 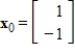 converges.
converges.
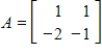 and vector
and vector 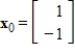 converges.
converges.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
74
The Shifted Inverse Power Method for an invertible n×nmatrix Ais implemented by applying the Power Method to 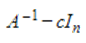 for some scalar c.
for some scalar c.
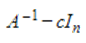 for some scalar c.
for some scalar c.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose 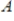 is a
is a 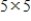 matrix having eigenvalues
matrix having eigenvalues 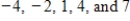
. Then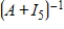 has dominant eigenvalue
has dominant eigenvalue 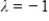
.
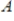 is a
is a 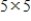 matrix having eigenvalues
matrix having eigenvalues 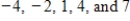
. Then
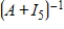 has dominant eigenvalue
has dominant eigenvalue 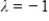
.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck


