Deck 1: Systems of Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 1: Systems of Linear Equations
1
Determine which of the points (2, -3), (2, 3), and (4, 2) lie on both of the lines
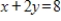 and
and
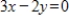
.
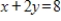 and
and 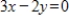
.
(2, 3)
2
Determine which of the points (1, 0, -1, 0), (0, 1, 2, 3), and (2, 1, -1, -1) satisfy the linear system
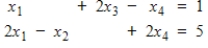
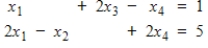
(0, 1, 2, 3)
3
Determine which of (3, s2, s1, 2), (0, 0, 0 ,0), (2 - s1 - s2, 1 + s1 + s2, s1, s2), and (3 - s1, s1, s2, 2 - s2) form a solution to the following system for all choices of the free parameters

.
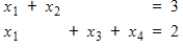

.
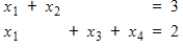
(2 - s1 - s2, 1 + s1 + s2, s1, s2)
4
Determine if the system is in echelon form, and if so, identify the leading variables and the free variables. If it is not in echelon form, explain why.
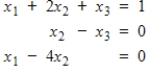
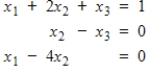

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
Determine if the system is in echelon form, and if so, identify the leading variables and the free variables. If it is not in echelon form, explain why.
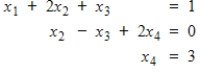
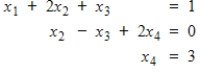

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Find all solutions to the system
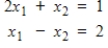
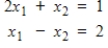

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Find all solutions to the system
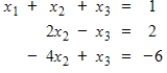
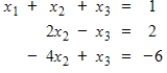

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
Find all solutions to the system
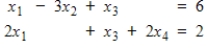
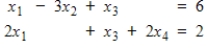

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Reorder the equations to put the following system of three equations with four unknowns in echelon form:
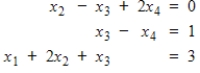
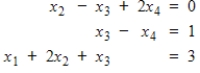

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
Determine the value(s) of
 so that the following system is consistent.
so that the following system is consistent.
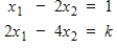
 so that the following system is consistent.
so that the following system is consistent.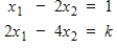

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose a system of
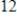 equations has two free variables. How many leading variables are there?
equations has two free variables. How many leading variables are there?
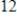 equations has two free variables. How many leading variables are there?
equations has two free variables. How many leading variables are there?
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
If a linear system has more variables than equations, then the system is inconsistent.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
If a linear system has infinitely many solutions, then there are more variables than equations.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
If a linear system has no free variables, then there exists at most one solution.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
Convert the augmented matrix to the equivalent linear system.
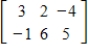
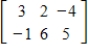

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
Convert the augmented matrix to the equivalent linear system.
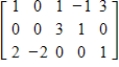
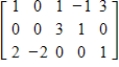

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether the matrix is in reduced echelon form, echelon form only, or not in echelon form.
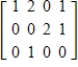
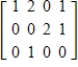

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the matrix is in reduced echelon form, echelon form only, or not in echelon form.



Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Determine whether the matrix is in reduced echelon form, echelon form only, or not in echelon form.



Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
Identify the row operation which transforms the matrix on the left to the matrix on the right.
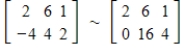
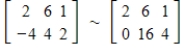

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Identify the row operation which transforms the matrix on the left to the matrix on the right.
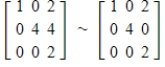
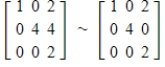

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Convert the given system to an augmented matrix, and find all solutions by reducing to echelon form and using back substitution.
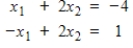
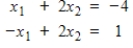

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Convert the given system to an augmented matrix, and find all solutions by reducing to echelon form and using back substitution.
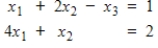
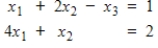

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
Convert the given system to an augmented matrix, and find all solutions by reducing to echelon form and using back substitution , if needed.
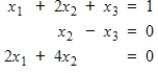
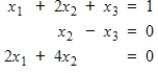

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
Convert the given system to an augmented matrix, and find all solutions by transforming to reduced echelon form and using back substitution.
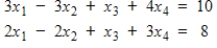
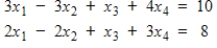

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Convert the given system to an augmented matrix, and find all solutions by transforming to reduced echelon form and using back substitution.
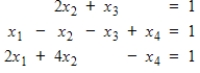
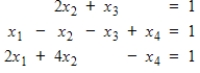

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
Every homogeneous linear system has at least one solution.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
A linear system with infinitely many solutions must have more variables than equations.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
A linear system with a unique solution can not have more variables than equations.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
The volume of traffic for a collection of intersections is shown. Find all possible values for
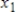
,

,

, and
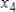
.
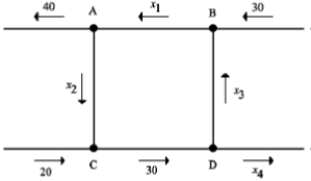
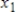
,

,

, and
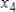
.


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
The volume of traffic for a collection of intersections is shown. Find the minimum volume of traffic from C to D. 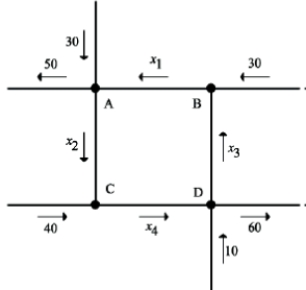


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
Find all possible equilibrium and endpoint temperatures for the heavy wires with endpoints held at the indicated temperatures.
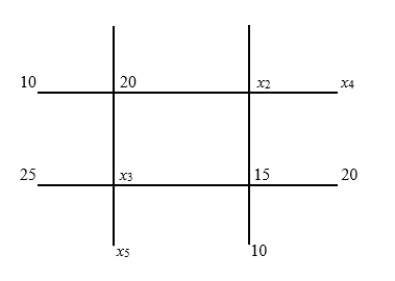


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Find the equilibrium temperatures for the heavy wires with endpoints held at the given temperatures.
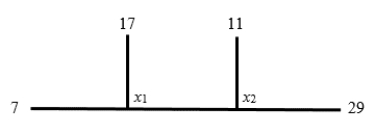


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
An economy has three industries: A, B, and C. These industries have annual consumer sales of 45, 37, and 64 (in millions of dollars), respectively. In addition, for every dollar of goods that A sells, A requires 25 cents from B and 15 cents from C. For each dollar of goods that B sells, B requires 35 cents from A and 25 cents from C. For each dollar of goods that C sells, C requires 20 cents from A and 45 cents from B. Let a, b, c be the total output from industries A, B, C, respectively. What values of a, b, c (rounded to the nearest thousand dollars) will satisfy both consumer and between-industry demand?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Balance the given chemical equation.
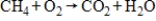
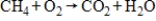

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
Balance the given chemical equation.
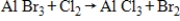
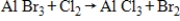

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Use a system of linear equations to find the values
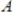 and
and
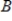 for the partial fraction decomposition
for the partial fraction decomposition
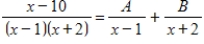
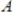 and
and 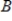 for the partial fraction decomposition
for the partial fraction decomposition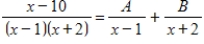

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Use a system of linear equations to find the values
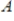
,
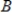
, and
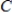 for the partial fraction decomposition
for the partial fraction decomposition
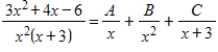
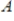
,
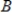
, and
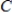 for the partial fraction decomposition
for the partial fraction decomposition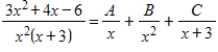

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
The points (-6, 0, -1), (3, 2, 0), and (0, 3, -1) lie on a plane ax + by + cz = 1. Use a system of linear equations to find the equation of this plane.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Use a system of linear equations to find the equation
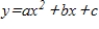 of the parabola which passes through the points (1, 2), (2, 0), and (3, -4).
of the parabola which passes through the points (1, 2), (2, 0), and (3, -4).
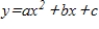 of the parabola which passes through the points (1, 2), (2, 0), and (3, -4).
of the parabola which passes through the points (1, 2), (2, 0), and (3, -4).
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
Use a system of linear equations to find a function of the form
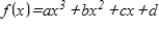 such that
such that
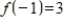
,
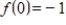
,
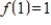
, and
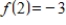
.
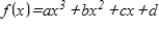 such that
such that 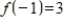
,
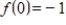
,
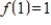
, and
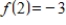
.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
Use a system of linear equations to find the values of the coefficients a, b, c if
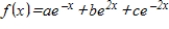 with
with
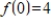
,
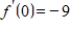
, and
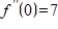
.
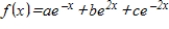 with
with 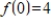
,
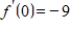
, and
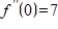
.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
Use partial pivoting with Gaussian elimination to find the solutions to the system.
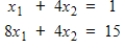
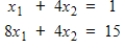

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
Use partial pivoting with Gaussian elimination to find the solutions to the system.
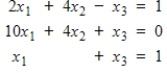
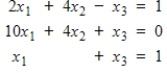

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the given system using Gaussian elimination with three significant digits of accuracy. Then solve the system again, incorporating partial pivoting.
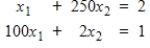
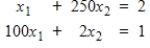

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the given system using Gaussian elimination with three significant digits of accuracy. Then solve the system again, incorporating partial pivoting.
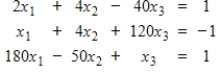
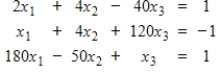

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Compute the first three Jacobi iterations, using
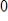 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
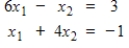
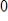 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.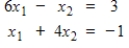

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
Compute the first three Jacobi iterations, using
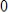 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
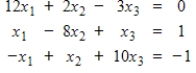
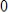 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.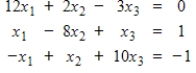

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
Compute the first three Gauss-Seidel iterations for the system in question 5, using
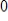 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
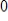 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
Compute the first three Gauss-Seidel iterations for the system in question 6, using
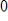 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
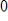 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Determine if the system is diagonally dominant. If not, then if possible rewrite the system so that it is diagonally dominant.
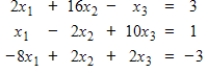
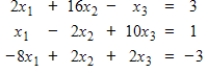

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Compute the first four Jacobi iterations for the system as written, with the initial value of each variable set equal to
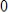
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Jacobi iterations. Finally, find the exact solution and compare.
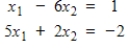
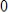
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Jacobi iterations. Finally, find the exact solution and compare.
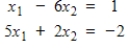

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
Compute the first four Jacobi iterations for the system as written, with the initial value of each variable set equal to
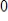
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Jacobi iterations. Finally, find the exact solution and compare.
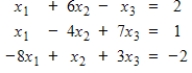
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Jacobi iterations. Finally, find the exact solution and compare.
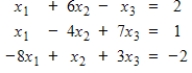

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
Compute the first four Gauss-Seidel iterations for the system in question 10, with the initial value of each variable set equal to 0. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Gauss-Seidel iterations.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
Compute the first four Gauss-Seidel iterations for the system in question 11, with the initial value of each variable set equal to
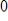
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Gauss-Seidel iterations.
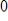
. Then rewrite the system so that it is diagonally dominant, set the value of each variable to 0, and again compute four Gauss-Seidel iterations.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
The values for the first few Jacobi iterations for a linear system are given. Find the values for the next iteration.
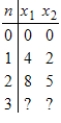


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
The values for the first few Gauss-Seidel iterations for a linear system are given. Find the values for the next iteration.



Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck


