Deck 10: Inner Product Spaces
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/45
Play
Full screen (f)
Deck 10: Inner Product Spaces
1
Evaluate the given inner product on
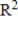 for
for
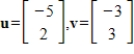
.
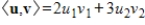
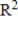 for
for 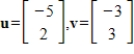
.
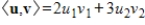
48
2
Evaluate the given inner product on
 for
for
.
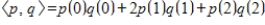
.
 for
for 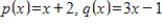
.
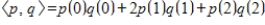
.
30
3
Evaluate the given inner product on
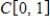 for
for
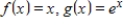
.
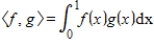
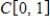 for
for 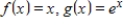
.
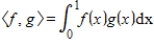
1
4
Evaluate the given inner product on
 for
for
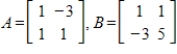
.
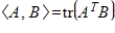
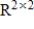 for
for 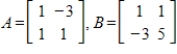
.
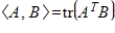

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate
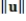
, where the inner product on
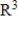 is
is
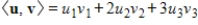 for
for
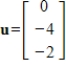
.
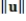
, where the inner product on
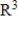 is
is 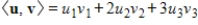 for
for 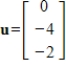
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate
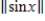
, where the inner product on
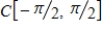 is
is
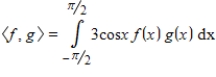
.
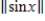
, where the inner product on
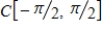 is
is 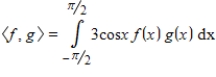
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
7
Determine
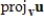
, where
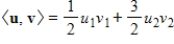 and
and
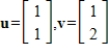
.
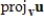
, where
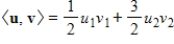 and
and 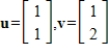
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
8
Determine
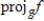
, where
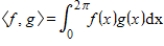 and
and
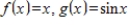
.
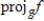
, where
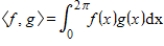 and
and 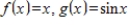
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
9
Determine
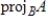
, where
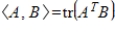 and
and
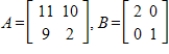
.
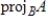
, where
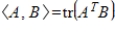 and
and 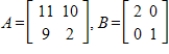
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
10
Determine all values of a such that in
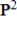 the vectors
the vectors
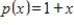 and
and
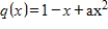 are orthogonal with respect to the inner product
are orthogonal with respect to the inner product
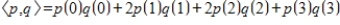
.
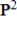 the vectors
the vectors 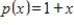 and
and 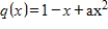 are orthogonal with respect to the inner product
are orthogonal with respect to the inner product 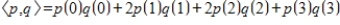
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
11
If
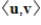 is an inner product on a vector space V, and v is any vector in V, then
is an inner product on a vector space V, and v is any vector in V, then
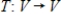 defined by
defined by
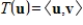 is a linear transformation.
is a linear transformation.
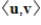 is an inner product on a vector space V, and v is any vector in V, then
is an inner product on a vector space V, and v is any vector in V, then 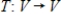 defined by
defined by 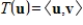 is a linear transformation.
is a linear transformation.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
12
If
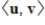 is an inner product on a vector space V, and
is an inner product on a vector space V, and
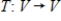 is an invertible linear transformation, then
is an invertible linear transformation, then
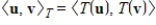 is also an inner product on V.
is also an inner product on V.
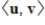 is an inner product on a vector space V, and
is an inner product on a vector space V, and 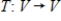 is an invertible linear transformation, then
is an invertible linear transformation, then 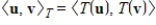 is also an inner product on V.
is also an inner product on V.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
13
If u, v are vectors in an inner product space V, then u is orthogonal to v if and only if
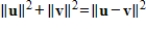
.
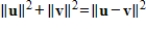
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
14
The following is an inner product on
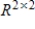
:
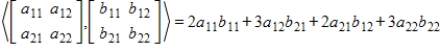
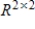
:
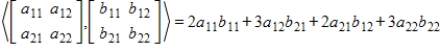

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
15
If
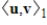 and
and
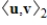 are both inner products on a vector space V, then
are both inner products on a vector space V, then
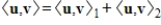 is also an inner product on V.
is also an inner product on V.
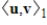 and
and 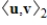 are both inner products on a vector space V, then
are both inner products on a vector space V, then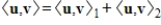 is also an inner product on V.
is also an inner product on V.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
16
Let
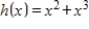
,
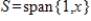
, and let the inner product on
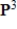 be given by
be given by
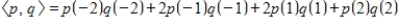
.
Use the fact that
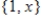 is an orthogonal basis for S to find
is an orthogonal basis for S to find
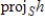
.
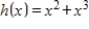
,
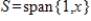
, and let the inner product on
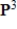 be given by
be given by 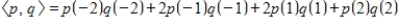
.
Use the fact that
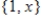 is an orthogonal basis for S to find
is an orthogonal basis for S to find 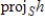
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
17
Let
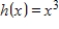
,
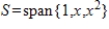
, and let the inner product on
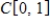 be given by
be given by
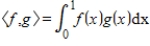
.
Use the fact that
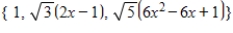 is an orthonormal basis for S to find
is an orthonormal basis for S to find
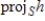
.
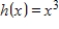
,
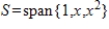
, and let the inner product on
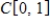 be given by
be given by 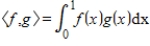
.
Use the fact that
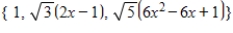 is an orthonormal basis for S to find
is an orthonormal basis for S to find 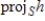
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
18
Find
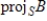
, where
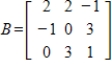
, where
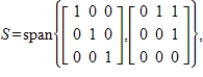
and the inner product on
 is
is
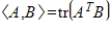
.
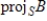
, where
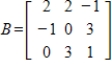
, where
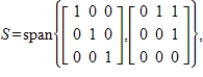
and the inner product on
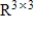 is
is 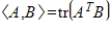
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
19
Use the Gram-Schmidt process to convert the set
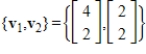 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product
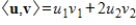
.
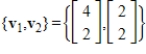 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product 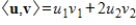
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
20
Use the Gram-Schmidt process to convert the set
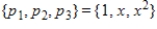 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product
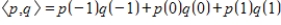
.
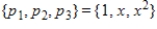 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product 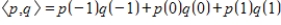
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
21
Use the Gram-Schmidt process to convert the set
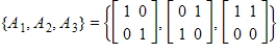 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product
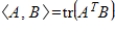
.
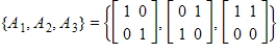 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product 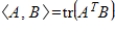
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
22
Use the Gram-Schmidt process to convert the set
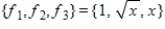 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product
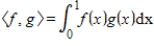
.
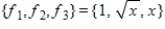 to an orthonormal basis with respect to the inner product
to an orthonormal basis with respect to the inner product 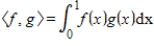
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
23
Let
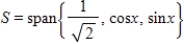 be a subspace of
be a subspace of
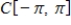
. Let
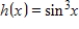
. Find
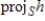 with respect to the inner product
with respect to the inner product
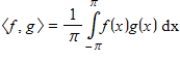
.
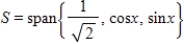 be a subspace of
be a subspace of 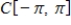
. Let
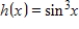
. Find
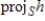 with respect to the inner product
with respect to the inner product 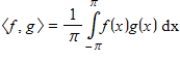
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
24
Determine the values of a (if any) that will make the given set of vectors orthogonal in
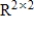 with respect to the inner product
with respect to the inner product
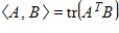
.
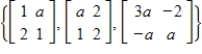
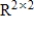 with respect to the inner product
with respect to the inner product 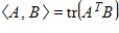
.
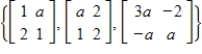

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
25
Determine the values of a (if any) that will make the given set of vectors orthogonal in
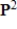 with respect to the inner product
with respect to the inner product
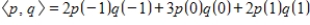
.
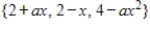
 with respect to the inner product
with respect to the inner product 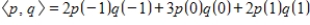
.
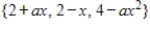

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
26
If
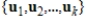 is an orthonormal set in an inner product space V, then
is an orthonormal set in an inner product space V, then
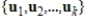 is linearly independent.
is linearly independent.
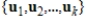 is an orthonormal set in an inner product space V, then
is an orthonormal set in an inner product space V, then 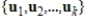 is linearly independent.
is linearly independent.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
27
If
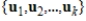 is a linear dependent set of nonzero vectors in a vector space V, and
is a linear dependent set of nonzero vectors in a vector space V, and
 is any inner product on V, then there exists
is any inner product on V, then there exists
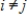 such that
such that
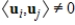
.
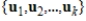 is a linear dependent set of nonzero vectors in a vector space V, and
is a linear dependent set of nonzero vectors in a vector space V, and  is any inner product on V, then there exists
is any inner product on V, then there exists 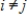 such that
such that 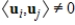
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
28
If
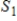 and
and
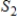 are nonzero subspaces of an inner product space V, and v is any vector in V, then
are nonzero subspaces of an inner product space V, and v is any vector in V, then
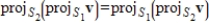
.
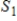 and
and 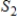 are nonzero subspaces of an inner product space V, and v is any vector in V, then
are nonzero subspaces of an inner product space V, and v is any vector in V, then 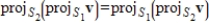
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
29
If V is a finite-dimensional inner product space, S is a nonzero subspace of V and
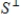 is nonzero, then for every
is nonzero, then for every
 in V,
in V,
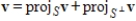
.
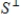 is nonzero, then for every
is nonzero, then for every  in V,
in V, 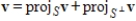
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
30
If
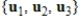 is an orthonormal set in an inner product space V, and
is an orthonormal set in an inner product space V, and
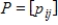 is a
is a
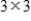 orthogonal matrix, then
orthogonal matrix, then
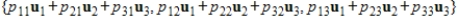 is also an orthonormal set in V.
is also an orthonormal set in V.
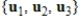 is an orthonormal set in an inner product space V, and
is an orthonormal set in an inner product space V, and 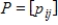 is a
is a 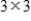 orthogonal matrix, then
orthogonal matrix, then 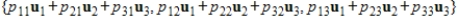 is also an orthonormal set in V.
is also an orthonormal set in V.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
31
Find the weighted least squares line for the data set
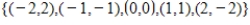
, with the inner three points weighted three times as much as the outer two points.
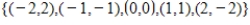
, with the inner three points weighted three times as much as the outer two points.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
32
Find the weighted least squares line for the data set
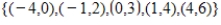
, with the inner three points weighted four times as much as the outer two points.
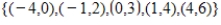
, with the inner three points weighted four times as much as the outer two points.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
33
Find the weighted least squares line for the data set
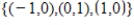
, with the inner point weighted t times as much as the outer two points.
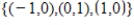
, with the inner point weighted t times as much as the outer two points.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
34
Find the Fourier approximation
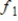 for
for
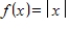
.
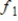 for
for 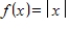
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
35
Find the Fourier approximation
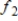 for
for
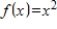
.
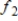 for
for 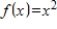
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
36
Find the Fourier approximation
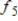 for the odd function
for the odd function
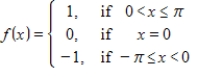
.
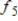 for the odd function
for the odd function 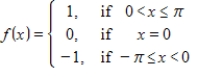
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
37
Find the discrete Fourier approximation
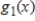 for
for
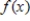 based on the table information.
based on the table information.
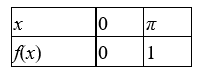
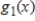 for
for 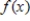 based on the table information.
based on the table information.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
38
Find the discrete Fourier approximation
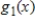 for
for
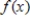 based on the table information.
based on the table information. 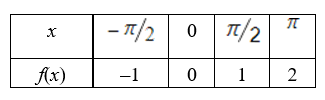
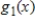 for
for 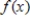 based on the table information.
based on the table information. 

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
39
Find the Fourier coefficients for the function
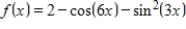 without computing any integrals.
without computing any integrals.
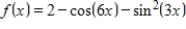 without computing any integrals.
without computing any integrals.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
40
Find the Fourier coefficients for the function
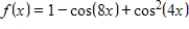 without computing any integrals.
without computing any integrals.
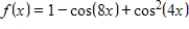 without computing any integrals.
without computing any integrals.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
41
In a weighted least squares regression, the average of the weights must equal 1.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
42
If f is a positive even function on
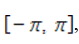
, then for every k,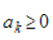 and
and 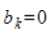 in the Fourier approximation of f.
in the Fourier approximation of f.
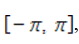
, then for every k,
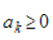 and
and 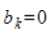 in the Fourier approximation of f.
in the Fourier approximation of f.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
43
If function
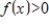 on
on
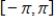
, then the discrete Fourier coefficient
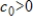
.
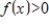 on
on 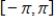
, then the discrete Fourier coefficient
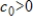
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
44
If f is an odd function on
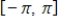
, then in the Fourier approximation of f, we have
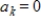 for every k.
for every k.
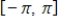
, then in the Fourier approximation of f, we have
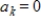 for every k.
for every k.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
45
If
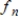 is the nth-order Fourier approximation to f, and
is the nth-order Fourier approximation to f, and
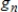 is the nth-order Fourier approximation to g, and
is the nth-order Fourier approximation to g, and
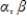 are scalars, then the nth-order Fourier approximation to
are scalars, then the nth-order Fourier approximation to
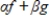 is
is
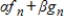
.
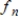 is the nth-order Fourier approximation to f, and
is the nth-order Fourier approximation to f, and 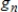 is the nth-order Fourier approximation to g, and
is the nth-order Fourier approximation to g, and 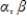 are scalars, then the nth-order Fourier approximation to
are scalars, then the nth-order Fourier approximation to 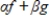 is
is 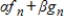
.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck


