Deck 1: Multiple Comparison Procedures
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/7
Play
Full screen (f)
Deck 1: Multiple Comparison Procedures
1
A one-factor fixed-effects ANOVA is performed on data for 5 groups of unequal sizes, and H0 is rejected at the .05 level of significance. Using the Scheffe' procedure, test the contrast that
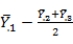 at the .05 level of significance given the following information:
at the .05 level of significance given the following information:
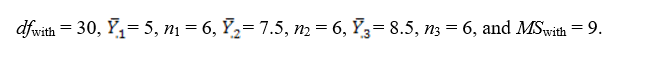
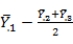 at the .05 level of significance given the following information:
at the .05 level of significance given the following information: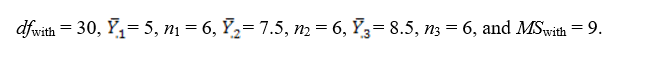
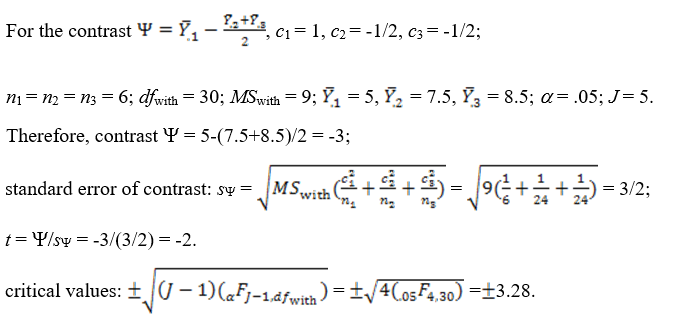 Because |t| = 2 < 3.28, we fail to reject the null hypothesis and conclude that the contrast is not significant at the .05 level of significance.
Because |t| = 2 < 3.28, we fail to reject the null hypothesis and conclude that the contrast is not significant at the .05 level of significance. 2
A one-factor fixed-effects ANOVA is performed on data from three groups of equal size (n = 15) and equal variances, and H0 is rejected at the .05 level. The following values were computed: MSwith = 60 and the sample means are.
= 25, = 20, and = 12. Use the Tukey HSD method to test all possible pairwise contrasts ( = .05)
= 25, = 20, and = 12. Use the Tukey HSD method to test all possible pairwise contrasts ( = .05)
Because , there are three possible pairwise contrasts: 1 vs. 2,1 vs. 3,2 vs. 3 .
For each contrast, , where and are two group means to be compared.
Because standard error
-
- Using Tukey HSD, the critical values are qdf
(with), J = .05q60, 3 = 3.40.
q1 < critical q, so 1 - 2 is not statistically significant at = .05.
q2 > critical q, q3 > critical q, so 1 - 3, 2 - 3 are statistically significant at = .05.
3
Which of the following linear combinations of population means is a legitimate contrast?
A) 1- 2/2+ 3/2
B) ( 1+ 2/2+ 3
C) ( 1+ 2)+ 3
D) 1- 2- 3
A) 1- 2/2+ 3/2
B) ( 1+ 2/2+ 3
C) ( 1+ 2)+ 3
D) 1- 2- 3
( 1+ 2)+ 3
4
If J = 3, which of the following sets of contrasts is orthogonal?
A) 1- 2, 1- 3
B) 2- 3, 2+ 3
C) 1- 3, 1-( 2+ 3)/2
D) 1- 3, 2-( 2+ 3)/2
A) 1- 2, 1- 3
B) 2- 3, 2+ 3
C) 1- 3, 1-( 2+ 3)/2
D) 1- 3, 2-( 2+ 3)/2

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
5
A researcher used Fisher's LSD to test three contrasts: 1- 2, 1- 3, 1-( 2+ 3)/2. Evaluate this practice.
A) This practice is problematic because Fisher's LSD is always too liberal.
B) This practice is problematic because Fisher's LSD can only be used to test simple
Contrasts.
C) This practice is problematic because the contrasts are not orthogonal.
D) I do not see any problem with this practice. It is great!
A) This practice is problematic because Fisher's LSD is always too liberal.
B) This practice is problematic because Fisher's LSD can only be used to test simple
Contrasts.
C) This practice is problematic because the contrasts are not orthogonal.
D) I do not see any problem with this practice. It is great!

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
6
In an experiment, =10, =20, and =40. Tukey HSD shows that 2- 1 is a significant contrast. What will you find out about 3- 1 and 3- 2 if the same procedure and same level are used?
A) Only 3- 1 is significant.
B) Only 3- 2 is significant.
C) Both contrasts are significant.
D) None of the contrasts are necessarily significant.
A) Only 3- 1 is significant.
B) Only 3- 2 is significant.
C) Both contrasts are significant.
D) None of the contrasts are necessarily significant.

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck
7
In an experiment,? =10, =200, and =4000. Which pairwise contrast will necessarily be significant
A) 2- 1
B) 3- 1
C) 3- 2
D) None of the contrasts will necessarily be significant.
A) 2- 1
B) 3- 1
C) 3- 2
D) None of the contrasts will necessarily be significant.

Unlock Deck
Unlock for access to all 7 flashcards in this deck.
Unlock Deck
k this deck


