Deck 14: One Factor Fixed-Effects Ancova With Single Covariate
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 14: One Factor Fixed-Effects Ancova With Single Covariate
1
A researcher wanted to examine if soil type had any effects on the heights of daylilies (Y). The thickness of the soil (X) in the pot was used as the covariate X. Given the data that follow, where there are three types of soil (n = 10 in each group), (a) calculate the adjusted mean values assuming that bw = 0.5, and (b) determine what effects the adjustment had on the posttest results.
(a) Adjusted mean: . We know that = 20, = 25, = 30; bw = 0.5; = 21, = 18, = 15. Because it's a balanced design, = (21 + 18 + 15)/3 = 18. We can calculate
20 ? 0.5*(21 - 18) = 18.5;
25 ? 0.5*(18 -18) = 25;
30 ? 0.5*(15- 18) = 31.5.
(b) The adjustment moved the mean for Group 1 down by 1.5 units (from 20 to 18.5), and moved the mean for Group 3 up by 1.5 units (from 30 to 31.5). It did not change the mean for Group 2. Therefore, after the adjustment the difference between group means is enlarged. The effects of soil type will become larger and possibly more significant.
20 ? 0.5*(21 - 18) = 18.5;
25 ? 0.5*(18 -18) = 25;
30 ? 0.5*(15- 18) = 31.5.
(b) The adjustment moved the mean for Group 1 down by 1.5 units (from 20 to 18.5), and moved the mean for Group 3 up by 1.5 units (from 30 to 31.5). It did not change the mean for Group 2. Therefore, after the adjustment the difference between group means is enlarged. The effects of soil type will become larger and possibly more significant.
2
A market researcher wanted to know whether different package designs for the same yogurt product would affect consumers' purchase intention. There were four different versions of package designs. Each package was viewed by eight participants, who then rated their likelihood to purchase the product. A one-factor ANCOVA was used to analyze the data where the covariate was the participants' liking of the yogurt product in general. Complete the following ANCOVA summary table ( = .05):
The factor (designs of cereal packages) has 4 levels, so J = 4. Each level has 8 participants, so n = 8, N = 4*8 = 32.
There is one covariate (liking of yogurt).
dfbetw(adj) = J - 1 = 4 - 1 = 3, dfwith(adj) = N - J - 1 = 32 - 4 - 1 = 27, dfcov = 1,dftotal = N - 1 = 32- 1 = 31.
SScov = dfcov*MScov = 1*5.6 = 5.6,
SSwith(adj) = SStotal -SSbetw(adj) -SScov = 35 - 10.5 ? 5.6 = 18.9.
MSbetw(adj) = SSbetw(adj)/dfbetw(adj) = 10.5/3 = 3.5.
MSwith(adj) = SSwith(adj)/dfwith(adj) = 18.9/27 = 0.7.
Fbetw(adj) = MSbetw(adj)/MSwith(adj) = 3.5/0.7 = 5; critical value = .05F3,27 = 2.96 < Fbetw(adj), reject H0.
Fcov = MScov/MSwith(adj) = 5.6/0.7 = 8; critical value = .05F1,27 = 4.21 < Fcov, reject H0.
There is one covariate (liking of yogurt).
dfbetw(adj) = J - 1 = 4 - 1 = 3, dfwith(adj) = N - J - 1 = 32 - 4 - 1 = 27, dfcov = 1,dftotal = N - 1 = 32- 1 = 31.
SScov = dfcov*MScov = 1*5.6 = 5.6,
SSwith(adj) = SStotal -SSbetw(adj) -SScov = 35 - 10.5 ? 5.6 = 18.9.
MSbetw(adj) = SSbetw(adj)/dfbetw(adj) = 10.5/3 = 3.5.
MSwith(adj) = SSwith(adj)/dfwith(adj) = 18.9/27 = 0.7.
Fbetw(adj) = MSbetw(adj)/MSwith(adj) = 3.5/0.7 = 5; critical value = .05F3,27 = 2.96 < Fbetw(adj), reject H0.
Fcov = MScov/MSwith(adj) = 5.6/0.7 = 8; critical value = .05F1,27 = 4.21 < Fcov, reject H0.
3
Mike wanted to examine whether people remembered information better with auditory cues or with visual cues. He recruited 14 participants and randomly assigned seven participants to each of the two groups: one group heard a list of words from headphones, and the other group saw the same list of words from the screen. The participants were then asked to write down as many words as they could remember. The dependent variable was the number of words correctly remembered (Y), and the covariate was the participants' score on a memory test (X) administered before the experiment. Using the data below, conduct an ANOVA on Y and an ANCOVA on Y using X as a covariate, and compare the results ( = .05). Determine the unadjusted and adjusted means.
Procedure:
Create a data set with three variables: Memory (covariate), Words (dependent variable), and Group (factor with 2 levels). The data set should have 14 cases.
To conduct ANOVA: Analyze General Linear Model Univariate.
Select Words as the Dependent Variable. Select Group as the Fixed Factor.
Go to Options. Select Group into Display Means for. Check Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
To conduct ANCOVA: Analyze General Linear Model Univariate.
Select Words as the Dependent Variable. Select Group as the Fixed Factor. Select Memory as the Covariate.
Click on Model. Under Sum of squares, select Type I from the dropdown menu. Click Continue.
Go to Options. Select Group into Display Means for.
Check Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
Selected SPSS Output:
I. ANOVA Results:
Tests of Between-Subjects Effects
Dependent Variable: Words
UnadjustedMeans
Dependent Variable: Words
II. ANCOVA Results:
Tests of Between-Subjects Effects
Dependent Variable: Words
Adjusted Means
Dependent Variable: Words
A one-factor fixed-effects ANOVA was first conducted. As shown in the table of unadjusted means, participants who received visual cues remembered more words (12.86) than those who received auditory cues did (10.43). However, the ANOVA table showed that the effect of type of cues on the number of words remembered was nonsignificant (F = 1.26, df = 1, 12, p = .28). The effect size was medium (partial 2=.095), but the observed power was not satisfactory (.179).
A one-factor ANCOVA was also conducted on the same data. As shown in the table of adjusted means, after adjusting for group differences in memory, the adjusted mean was 10.55 for people who received auditory cues and 12.74 for people who received visual cues. The one-factor ANCOVA table showed that the type of cues had a significant effect on the number of words remembered after adjusting for memory (F = 5.51, df = 1, 11, p = .039), with a large effect size (partial 2=.334).
The slope of Memory (i.e., the covariate) was also significantly different from zero (F = 55.10, df = 1, 11, p < .001), with large effect size and maximal power, suggesting that memory is related to the number of words remembered.
After Memory was included as covariate in the model, the mean for Group 1 was adjusted to be slightly higher than the raw mean, whereas the mean for Group 2 was adjusted to be slightly lower than the raw mean.
By substantially reducing error variance, the use of the covariate resulted in a larger difference between the groups, and increased power for the F test.
Create a data set with three variables: Memory (covariate), Words (dependent variable), and Group (factor with 2 levels). The data set should have 14 cases.
To conduct ANOVA: Analyze General Linear Model Univariate.
Select Words as the Dependent Variable. Select Group as the Fixed Factor.
Go to Options. Select Group into Display Means for. Check Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
To conduct ANCOVA: Analyze General Linear Model Univariate.
Select Words as the Dependent Variable. Select Group as the Fixed Factor. Select Memory as the Covariate.
Click on Model. Under Sum of squares, select Type I from the dropdown menu. Click Continue.
Go to Options. Select Group into Display Means for.
Check Descriptive statistics, Estimates of effect size, and Observed power. Click Continue.
Selected SPSS Output:
I. ANOVA Results:
Tests of Between-Subjects Effects
Dependent Variable: Words
UnadjustedMeans
Dependent Variable: Words
II. ANCOVA Results:
Tests of Between-Subjects Effects
Dependent Variable: Words
Adjusted Means
Dependent Variable: Words
A one-factor fixed-effects ANOVA was first conducted. As shown in the table of unadjusted means, participants who received visual cues remembered more words (12.86) than those who received auditory cues did (10.43). However, the ANOVA table showed that the effect of type of cues on the number of words remembered was nonsignificant (F = 1.26, df = 1, 12, p = .28). The effect size was medium (partial 2=.095), but the observed power was not satisfactory (.179).
A one-factor ANCOVA was also conducted on the same data. As shown in the table of adjusted means, after adjusting for group differences in memory, the adjusted mean was 10.55 for people who received auditory cues and 12.74 for people who received visual cues. The one-factor ANCOVA table showed that the type of cues had a significant effect on the number of words remembered after adjusting for memory (F = 5.51, df = 1, 11, p = .039), with a large effect size (partial 2=.334).
The slope of Memory (i.e., the covariate) was also significantly different from zero (F = 55.10, df = 1, 11, p < .001), with large effect size and maximal power, suggesting that memory is related to the number of words remembered.
After Memory was included as covariate in the model, the mean for Group 1 was adjusted to be slightly higher than the raw mean, whereas the mean for Group 2 was adjusted to be slightly lower than the raw mean.
By substantially reducing error variance, the use of the covariate resulted in a larger difference between the groups, and increased power for the F test.
4
Barbara wants to know whether students will learn most effectively with soft music as background sound, as opposed to loud music or no music at all. In the following table are three independent random samples (different background sounds) of paired values on the covariate (X; pretest score) and the dependent variable (Y; posttest score). Conduct an ANOVA on Y, an ANCOVA on Y using X as a covariate, and compare the results ( = .05). Determine the unadjusted and adjusted means.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
Dr. Green conducted an ANCOVA to determine whether hearing-impaired children who were taught sign language early on would develop better language skills compared to those who did not learn sign language. The data set contains two independent random samples (children who learned sign language and those who did not) of paired values on the covariate (X; child's hearing) and the dependent variable (Y; language skills measured when the child was three years old). Dr. Green also examined the data to see if the assumptions of ANCOVA were met. The following table and figures are the selected output from Dr. Green's analysis ( = .05):
Tests of Between-Subjects Effects
Dependent Variable: Language
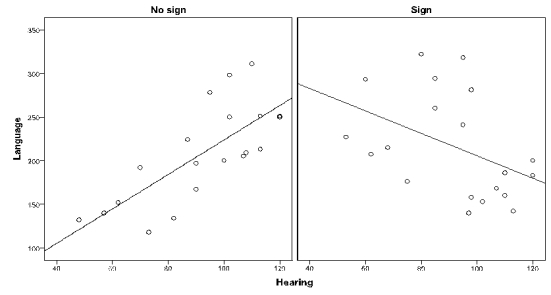
a. What assumption is being evaluated here?
b. Was this assumption satisfied? If not, what effect might it have on the results of ANCOVA?
Tests of Between-Subjects Effects
Dependent Variable: Language

a. What assumption is being evaluated here?
b. Was this assumption satisfied? If not, what effect might it have on the results of ANCOVA?

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
For which of the following situations is it appropriate to use ANCOVA?
A) In each group, half of the participants had a time limit to write the words down. Whether a time limit was imposed was also included in the model.
B) The participants' socioeconomic status (low, middle, or high) was expected to have an effect on their performance and was also included in the model.
C) Participants took a vocabulary test before the experiment and the scores of the test were included in the model.
D) Participants took a vocabulary test after the experiment and the scores of the test were included in the model.
A) In each group, half of the participants had a time limit to write the words down. Whether a time limit was imposed was also included in the model.
B) The participants' socioeconomic status (low, middle, or high) was expected to have an effect on their performance and was also included in the model.
C) Participants took a vocabulary test before the experiment and the scores of the test were included in the model.
D) Participants took a vocabulary test after the experiment and the scores of the test were included in the model.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose the researcher used IQ as the covariate. He then found that the mean IQ is slightly different across two groups, and people with higher IQ tended to remember more words than people with lower IQ. It seems likely that
A) the assumption of independence was violated.
B) the assumption of homogeneity of variance was violated.
C) the assumption of independence of covariate and treatment was violated.
D) the assumption of homogeneity of slopes was violated.
E) there is no indication of assumption violation.
A) the assumption of independence was violated.
B) the assumption of homogeneity of variance was violated.
C) the assumption of independence of covariate and treatment was violated.
D) the assumption of homogeneity of slopes was violated.
E) there is no indication of assumption violation.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose out of budget concerns, the researcher included only five participants in each group, tested each participant twice, and used each time as separate observations. It seems likely that
A) the assumption of independence was violated.
B) the assumption of homogeneity of variance was violated.
C) the assumption of independence of covariate and treatment was violated.
D) the assumption of homogeneity of slopes was violated.
E) there is no indication of assumption violation.
A) the assumption of independence was violated.
B) the assumption of homogeneity of variance was violated.
C) the assumption of independence of covariate and treatment was violated.
D) the assumption of homogeneity of slopes was violated.
E) there is no indication of assumption violation.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
A researcher wanted to examine if soil type had any effects on the heights of daylilies. Ten bulbs of daylilies were planted in each of the three different types of soil. The thickness of the soil X) was also measured for each pot. After three months, the heights of the plants
Y) were measured. Below are the group means of the study.
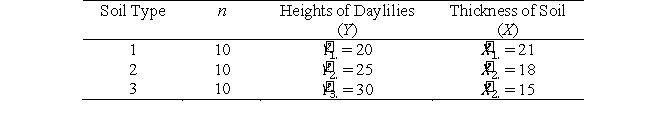
-If ANCOVA is used, which group will have the highest adjusted mean height?
A) Group 1 (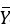 '1.)
'1.)
B) Group 2 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'2.)
C) Group 3 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'3.)
D) All groups would have the same adjusted mean.
E) Any of the above situations is possible (not enough information provided).
Y) were measured. Below are the group means of the study.
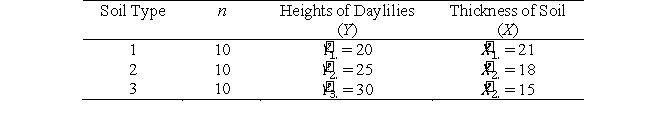
-If ANCOVA is used, which group will have the highest adjusted mean height?
A) Group 1 (
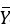 '1.)
'1.)B) Group 2 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'2.)
C) Group 3 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'3.)
D) All groups would have the same adjusted mean.
E) Any of the above situations is possible (not enough information provided).

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10
A researcher wanted to examine if soil type had any effects on the heights of daylilies. Ten bulbs of daylilies were planted in each of the three different types of soil. The thickness of the soil X) was also measured for each pot. After three months, the heights of the plants
Y) were measured. Below are the group means of the study.
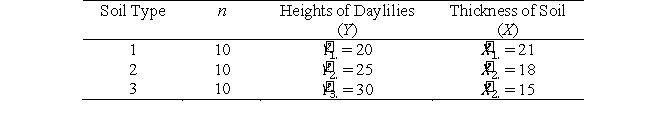
-If there is a substantial, positive correlation between the thickness of soil (X) and the height of daylilies (Y), which group will have the highest adjusted mean height?
A) Group 1 (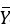 '1.)
'1.)
B) Group 2 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'2.)
C) Group 3 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'3.)
D) All groups would have the same adjusted mean.
E) Any of the above situations is possible.
Y) were measured. Below are the group means of the study.
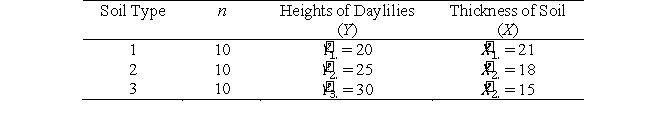
-If there is a substantial, positive correlation between the thickness of soil (X) and the height of daylilies (Y), which group will have the highest adjusted mean height?
A) Group 1 (
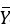 '1.)
'1.)B) Group 2 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'2.)
C) Group 3 (11ef2a2b_76aa_09e2_add3_99a954c0e1f4_TBR1344_11'3.)
D) All groups would have the same adjusted mean.
E) Any of the above situations is possible.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
A researcher wanted to examine if soil type had any effects on the heights of daylilies. Ten bulbs of daylilies were planted in each of the three different types of soil. The thickness of the soil X) was also measured for each pot. After three months, the heights of the plants
Y) were measured. Below are the group means of the study.
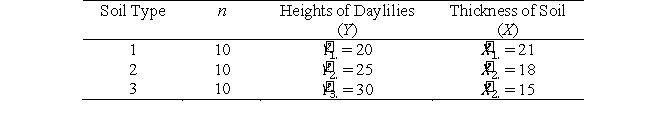
-If there is no correlation between X and Y, the MSwith for ANCOVA as compared to that for ANOVA will be
A) less.
B) the same.
C) greater.
D) unpredictably different.
Y) were measured. Below are the group means of the study.
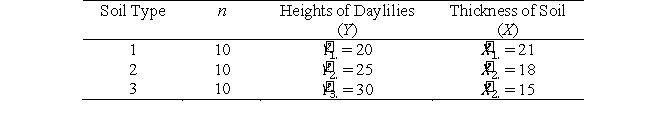
-If there is no correlation between X and Y, the MSwith for ANCOVA as compared to that for ANOVA will be
A) less.
B) the same.
C) greater.
D) unpredictably different.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
A researcher wanted to examine if soil type had any effects on the heights of daylilies. Ten bulbs of daylilies were planted in each of the three different types of soil. The thickness of the soil X) was also measured for each pot. After three months, the heights of the plants
Y) were measured. Below are the group means of the study.
-If there is a substantial negative correlation between X and Y, the error variation for ANCOVA as compared to that for ANOVA will be
A) less.
B) the same.
C) greater.
D) unpredictably different.
Y) were measured. Below are the group means of the study.
-If there is a substantial negative correlation between X and Y, the error variation for ANCOVA as compared to that for ANOVA will be
A) less.
B) the same.
C) greater.
D) unpredictably different.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13
A researcher wanted to examine if soil type had any effects on the heights of daylilies. Ten bulbs of daylilies were planted in each of the three different types of soil. The thickness of the soil X) was also measured for each pot. After three months, the heights of the plants
Y) were measured. Below are the group means of the study.
-If the correlation between X and Y is 0.5 for soil type 1, 0.1 for soil type 2, and ?0.5 for soil type 3, it seems likely that
A) the assumption of normality is violated.
B) the assumption of homogeneity of variance is violated.
C) the assumption of linearity is violated.
D) the assumption of homogeneity of slopes is violated.
E) there is no indication of assumption violation.
Y) were measured. Below are the group means of the study.
-If the correlation between X and Y is 0.5 for soil type 1, 0.1 for soil type 2, and ?0.5 for soil type 3, it seems likely that
A) the assumption of normality is violated.
B) the assumption of homogeneity of variance is violated.
C) the assumption of linearity is violated.
D) the assumption of homogeneity of slopes is violated.
E) there is no indication of assumption violation.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
14
In ANCOVA, suppose Y is the dependent variable, X is the covariate, and the factor has two levels. Also, all assumptions of ANCOVA are met. Which of the following situations is the most desirable?
A) rXY = 0.5; =10, =12, =11.
B) rXY = 0.1; =10, =12, =11.
C) rXY = -0.1; =10, =20, =15.
D) rXY = -0.5; =10, =20, =15.
A) rXY = 0.5; =10, =12, =11.
B) rXY = 0.1; =10, =12, =11.
C) rXY = -0.1; =10, =20, =15.
D) rXY = -0.5; =10, =20, =15.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
In a one-factor ANCOVA, suppose the factor has two levels (groups). Scatterplots of the dependent variable (Y) and the covariate (X) are generated (where group 1 is indicated by "•" and group 2 by "o"). Which of the following graphs shows the most desirable situation?
A)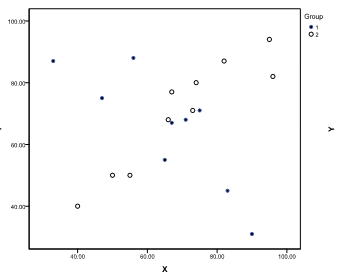
B)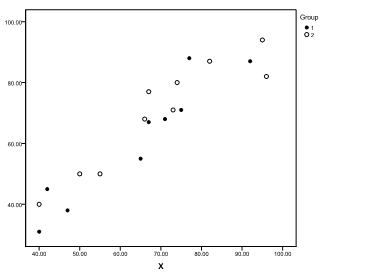
C)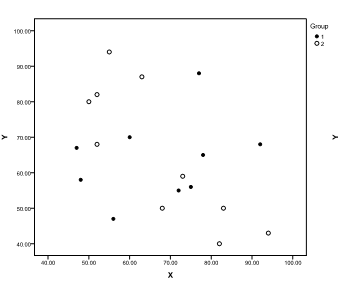
D)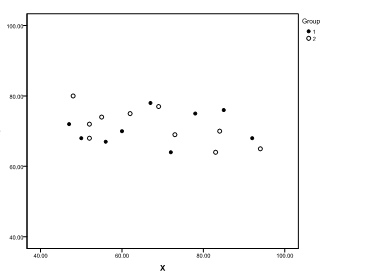
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16
Susan runs an ANOVA using the covariate X as the dependent variable and the factor A as the independent variable. Now using Y as the dependent variable, Susan runs another ANOVA to evaluate if there is any interaction between the covariate X and the factor A. For , which of the following situations is the most desirable?
A) p = 0.01
B) p = 0.05
C) p = 0.1
D) p = 0.5
A) p = 0.01
B) p = 0.05
C) p = 0.1
D) p = 0.5

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
The covariate in ANCOVA serves as which one of the following?
A) Dependent variable
B) Design control
C) Experimental control
D) Statistical control
A) Dependent variable
B) Design control
C) Experimental control
D) Statistical control

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
In ANCOVA, which of the following is a source of variation not controlled for when designing the experiment but that the researcher believes to affect the outcome?
A) Covariate
B) Dependent variable
C) Independent variable
D) None of the above
A) Covariate
B) Dependent variable
C) Independent variable
D) None of the above

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
The covariate in ANCOVA is also referred to as which one of the following?
A) Adjustment variable
B) Concomitant variable
C) Dependent variable
D) Independent variable
A) Adjustment variable
B) Concomitant variable
C) Dependent variable
D) Independent variable

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


