Deck 8: Essential Probability Rules
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/58
Play
Full screen (f)
Deck 8: Essential Probability Rules
1
What is the probability that an event will occur?
A)The number of successful outcomes divided by the number of unsuccessful outcomes
B)The number of successful outcomes divided by the total number of outcomes
C)The number of unsuccessful outcomes divided by the number of successful outcomes
D)The number of unsuccessful outcomes divided by the total number of outcomes
A)The number of successful outcomes divided by the number of unsuccessful outcomes
B)The number of successful outcomes divided by the total number of outcomes
C)The number of unsuccessful outcomes divided by the number of successful outcomes
D)The number of unsuccessful outcomes divided by the total number of outcomes
B
2
A population has an equal proportion of males and females. That is, when randomly selecting one individual, the probability that the individual is male (M) is ½ and the probability that the individual is female (F) is ½ Each of the outcomes M and F have a probability ½ of occurring. What does this mean?
A)In the next four randomly selected individuals, exactly two of the outcomes will be M.
B)In the next four randomly selected individuals, the outcomes will alternate between MFMF and FMFM.
C)In the next four randomly selected individuals, they cannot all be the same outcome.
D)In the next four randomly selected individuals, the outcomes could be any combination of M and F
A)In the next four randomly selected individuals, exactly two of the outcomes will be M.
B)In the next four randomly selected individuals, the outcomes will alternate between MFMF and FMFM.
C)In the next four randomly selected individuals, they cannot all be the same outcome.
D)In the next four randomly selected individuals, the outcomes could be any combination of M and F
D
3
A population has an equal proportion of males and females. That is, when randomly selecting one individual, the probability that the individual is male (M) is ½ and the probability that the individual is female (F) is ½ There are only two outcomes when an individual is selected: {M, F}. What is this collection of all possible outcomes called?
A)A census
B)The population
C)The sample space
D)The distribution
A)A census
B)The population
C)The sample space
D)The distribution
C
4
A population has an equal proportion of males and females. That is, when randomly selecting one individual, the probability that the individual is male (M) is ½ and the probability that the individual is female (F) is ½. In the first 50 randomly selected individuals, 20 were male. In the next 50 randomly selected individuals, which of the following must happen?
A)More than half of the individuals will be males to balance out the small number of males in the first 50 individuals. However, the order in which these males will be selected is unpredictable.
B)More than 20 of the individuals will be males because the proportion of males after 100 individuals must be closer to ½
C)The number of males will be very close to 30 in the next 50 individuals because the proportion must be close to ½
D)The number of males could be any value from 0 to 30 in the next 50 individuals because each individual is independent of the others.
A)More than half of the individuals will be males to balance out the small number of males in the first 50 individuals. However, the order in which these males will be selected is unpredictable.
B)More than 20 of the individuals will be males because the proportion of males after 100 individuals must be closer to ½
C)The number of males will be very close to 30 in the next 50 individuals because the proportion must be close to ½
D)The number of males could be any value from 0 to 30 in the next 50 individuals because each individual is independent of the others.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
5
Studies indicate that approximately 7% of Americans are vegetarians. If an American is selected at random, what is the probability that he or she is NOT a vegetarian?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following defines an event considered to have an unusual probability?
A)The probability exceeds 1.
B)The probability is a negative number.
C)The probability is very low.
D)The probability equals 1.
A)The probability exceeds 1.
B)The probability is a negative number.
C)The probability is very low.
D)The probability equals 1.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
7
A researcher is trying to determine the proportion of a certain species of fish in a local lake. After sampling 40 fish, she found 32 of them were the species of interest. What does she estimate as the probability that the next randomly selected fish will be of the species of interest?
A)0.32
B)0.50
C)0.80
D)1.25
A)0.32
B)0.50
C)0.80
D)1.25

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
8
The Centers for Disease Control and Prevention receives information about the causes for HIV/AIDS infection in the United States. Here are the causes of infection and their respective probability among American women age 20 to 24 years:
?
?
This is a legitimate probability model. Therefore, what must be the probability that an American woman age 20 to 24 was infected via injection drug use?
A)0.116
B)0.186
C)0.206
D)0.250
?
?
This is a legitimate probability model. Therefore, what must be the probability that an American woman age 20 to 24 was infected via injection drug use?
A)0.116
B)0.186
C)0.206
D)0.250

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
9
The Centers for Disease Control and Prevention receives information about the causes for HIV/AIDS infection in the United States. Here are the causes of infection and their respective probability among American women age 20 to 24 years:
?
?
What is the probability that an American woman age 20 to 24 contracted HIV/AIDS either via heterosexual sex or via perinatal infection?
A)0.083
B)0.211
C)0.500
D)0.789
?
?
What is the probability that an American woman age 20 to 24 contracted HIV/AIDS either via heterosexual sex or via perinatal infection?
A)0.083
B)0.211
C)0.500
D)0.789

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following terms describes an event that is uncertain but has a regular distribution over many outcomes?
A)Random
B)Predictable
C)Deterministic
D)Chaotic
A)Random
B)Predictable
C)Deterministic
D)Chaotic

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
11
Event A has probability 0.4. Event B has probability 0.5. If A and B are disjoint, what is the probability that both events occur?
A)0.0
B)0.1
C)0.2
D)0.9
A)0.0
B)0.1
C)0.2
D)0.9

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
12
Event A has probability 0.4. Event B has probability 0.5. If A and B are disjoint, what is the probability of A or B?
A)0.0
B)0.1
C)0.2
D)0.9
A)0.0
B)0.1
C)0.2
D)0.9

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
13
Event A has probability 0.4. Event B has probability 0.5. Event C has probability 0.6. Which of the following statements about these events must be TRUE?
A)Events A, B, and C are disjoint.
B)One event must have some outcomes in common with at least one other event.
C)The probability that event C does not occur is 0.9.
D)The sample space for these events is larger than typical.
A)Events A, B, and C are disjoint.
B)One event must have some outcomes in common with at least one other event.
C)The probability that event C does not occur is 0.9.
D)The sample space for these events is larger than typical.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
14
Event A occurs with probability 0.2. Event B occurs with probability 0.3. Event C occurs with probability 0.4. If A, B, and C are disjoint, then which of the following probabilities is (are) correct?
A)P(A or B) = 0.5
B)P(A or C) = 0.6
C)P(A or B or C) = 0.9
D)All of these choices are correct.
A)P(A or B) = 0.5
B)P(A or C) = 0.6
C)P(A or B or C) = 0.9
D)All of these choices are correct.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
15
Based on a recent Gallup survey, we define the following probability model for the number X of daily cups of coffee consumed by Americans.
?
?
What is the probability that an American consumes 4 or more cups of coffee daily?
A)0.10
B)1/5
C)1/4
D)Impossible to determine from the information given
?
?
What is the probability that an American consumes 4 or more cups of coffee daily?
A)0.10
B)1/5
C)1/4
D)Impossible to determine from the information given

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
16
Based on a recent Gallup survey, we define the following probability model for the number X of daily cups of coffee consumed by Americans.
What is the probability that an American does NOT consume 2 cups of coffee daily?
What is the probability that an American does NOT consume 2 cups of coffee daily?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
17
Based on a recent Gallup survey, we define the following probability model for the number X of daily cups of coffee consumed by Americans.
What is the probability that an American consumes at most 1 cup of coffee daily?
What is the probability that an American consumes at most 1 cup of coffee daily?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
18
What is the term for a variable whose value is a numerical outcome of a random phenomenon?
A)Random variable
B)Parameter
C)Biased
D)Random sample
A)Random variable
B)Parameter
C)Biased
D)Random sample

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
19
A physician observes the number of lesions on subjects who regularly used tanning salons. Let X be the number of lesions observed. The physician found that X had the following probability distribution.
?
?
What is the probability that a randomly chosen subject has at least three lesions?
A)0.3
B)0.4
C)0.6
D)0.7
?
?
What is the probability that a randomly chosen subject has at least three lesions?
A)0.3
B)0.4
C)0.6
D)0.7

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
20
A physician observes the number of lesions on subjects who regularly used tanning salons. Let X be the number of lesions observed. The physician found that X had the following probability distribution.
?
?
What is the value of P(X > 3)?
A)0.3
B)0.4
C)0.6
D)0.7
?
?
What is the value of P(X > 3)?
A)0.3
B)0.4
C)0.6
D)0.7

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
21
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
This is a legitimate probability model. Therefore, what is the value of P(X = 7)?
A)1/7
B)1/8
C)0.43
D)0.57
?
?
This is a legitimate probability model. Therefore, what is the value of P(X = 7)?
A)1/7
B)1/8
C)0.43
D)0.57

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
22
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
What does the event X < 5 mean?
A)The student watched TV no more than 5 days in the past week.
B)The student watched TV at least 5 days in the past week.
C)The probability that the student watched TV in the past week is smaller than 5.
D)The student watched TV fewer than 5 days in the past week.
?
?
What does the event X < 5 mean?
A)The student watched TV no more than 5 days in the past week.
B)The student watched TV at least 5 days in the past week.
C)The probability that the student watched TV in the past week is smaller than 5.
D)The student watched TV fewer than 5 days in the past week.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
23
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
What is the probability that X < 5?
A)0.08
B)1/8
C)0.30
D)0.38
?
?
What is the probability that X < 5?
A)0.08
B)1/8
C)0.30
D)0.38

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
24
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
What is the correct notation for "watched TV at least two days in the past week" in terms of X?
A)X > 1
B)X > 2
C)X = 2
D)X < 1
?
?
What is the correct notation for "watched TV at least two days in the past week" in terms of X?
A)X > 1
B)X > 2
C)X = 2
D)X < 1

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
25
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
What is the probability that a randomly selected student watched TV at least two days in the past week?
A)2/7
B)5/8
C)0.87
D)0.93
?
?
What is the probability that a randomly selected student watched TV at least two days in the past week?
A)2/7
B)5/8
C)0.87
D)0.93

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
26
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
What is the probability that a randomly selected student did not watch TV 7 days in the past week?
A)0.43
B)0.57
C)6/7
D)7/8
?
?
What is the probability that a randomly selected student did not watch TV 7 days in the past week?
A)0.43
B)0.57
C)6/7
D)7/8

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
27
Some argue that millions of Americans are so hooked on television that their viewing habits fit the criteria for substance abuse, as defined in the official psychiatric manual. Choose a young person (age 19 to 25) at random and ask, "In the past seven days, how many days did you watch television?" Call the response X for short. Here is a probability model for the response:
?
?
For a randomly selected student, which of the following terms describes the events X = 3 and X = 4?
A)Disjoint
B)Not disjoint
C)Independent
D)Complementary
?
?
For a randomly selected student, which of the following terms describes the events X = 3 and X = 4?
A)Disjoint
B)Not disjoint
C)Independent
D)Complementary

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
28
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
What is the probability of getting exactly 3 color-blind individuals in the sample?
A)0.000
B)0.019
C)0.111
D)0.125
?
?
What is the probability of getting exactly 3 color-blind individuals in the sample?
A)0.000
B)0.019
C)0.111
D)0.125

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
29
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
What is the probability of getting at least 6 color-blind individuals in the sample?
A)0.000
B)0.333
C)0.375
D)1.000
?
?
What is the probability of getting at least 6 color-blind individuals in the sample?
A)0.000
B)0.333
C)0.375
D)1.000

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
30
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
What is the probability of getting 2 or 3 color-blind individuals in the sample?
A)0.039
B)0.128
C)0.466
D)0.870
?
?
What is the probability of getting 2 or 3 color-blind individuals in the sample?
A)0.039
B)0.128
C)0.466
D)0.870

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
31
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
Which is the correct notation for representing the probability of getting at least 4 color-blind individuals in the sample?
A)P(X < 4)
B)P(X > 4)
C)P(X ?4)
D)P(X ? 4)
?
?
Which is the correct notation for representing the probability of getting at least 4 color-blind individuals in the sample?
A)P(X < 4)
B)P(X > 4)
C)P(X ?4)
D)P(X ? 4)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
32
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
What is the mean of this distribution?
A)0.640
B)0.766
C)0.096
D)None of these choices is correct.
?
?
What is the mean of this distribution?
A)0.640
B)0.766
C)0.096
D)None of these choices is correct.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
33
The frequency of color blindness (dyschromatopsia) in the Caucasian American male population is estimated to be about 8%. Let's call X the number of color-blind individuals in a random sample of 8 Caucasian American males. The table gives the probability distribution for X.
?
?
What is the standard deviation of this distribution?
A)0.64
B)0.766
C)0.096
D)None of these choices is correct.
?
?
What is the standard deviation of this distribution?
A)0.64
B)0.766
C)0.096
D)None of these choices is correct.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
34
Based on data from the U.S. Department of Agriculture, we define the following probability model for the number X of different pesticides detected in fresh produce.
What is the numerical value for the probability P(X < 2)?
What is the numerical value for the probability P(X < 2)?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
35
Based on data from the U.S. Department of Agriculture, we define the following probability model for the number X of different pesticides detected in fresh produce.
?
In this context, the probability P(X < 2) is also equal to which of these probabilities?
A)P(X ? 2)
B)P(X ? 3)
C)P(X ? 1)
D)P(X = 1)
?
In this context, the probability P(X < 2) is also equal to which of these probabilities?
A)P(X ? 2)
B)P(X ? 3)
C)P(X ? 1)
D)P(X = 1)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
36
If X is a continuous uniform random variable taking values between 0 and 100, what is the numerical value of the probability P(X = 10.333)?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
37
The expected value of a probability distribution is equal to
A)The standard deviation.
B)The mean.
C)The variance.
D)The value cannot be found because all the probabilities are different.
A)The standard deviation.
B)The mean.
C)The variance.
D)The value cannot be found because all the probabilities are different.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
38
The probability density of a random variable X is given in the figure.
From this density, what is the probability that X is between 0.5 and 1.5?
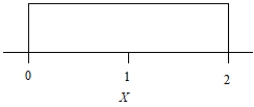
A)1/3
B)1/2
C)3/4
D)1
From this density, what is the probability that X is between 0.5 and 1.5?
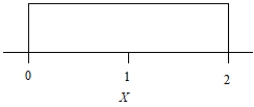
A)1/3
B)1/2
C)3/4
D)1

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
39
The probability density of a random variable X is given in the figure.
What is the probability that X is at least 1.5?
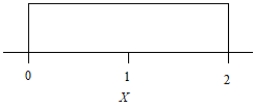
A)0
B)1/4
C)1/3
D)1/2
What is the probability that X is at least 1.5?
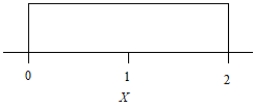
A)0
B)1/4
C)1/3
D)1/2

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
40
The probability density of a random variable X is given in the figure.
What is the probability that X = 1.5?
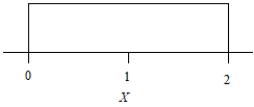
A)0
B)1/4
C)1/3
D)1/2
What is the probability that X = 1.5?
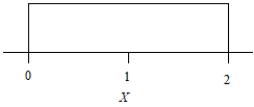
A)0
B)1/4
C)1/3
D)1/2

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
41
The probability density of a random variable X is given in the figure.
What is the median of the distribution of X?
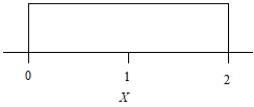
A)0
B)1
C)2
D)Impossible to calculate from the graph
What is the median of the distribution of X?
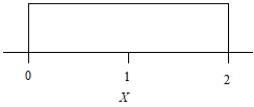
A)0
B)1
C)2
D)Impossible to calculate from the graph

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
42
The probability density of a random variable X is given in the figure.
What is the value of P(0 < X ≤ 2)?
A)0.0
B)0.5
C)1.0
D)2.0
What is the value of P(0 < X ≤ 2)?
A)0.0
B)0.5
C)1.0
D)2.0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following statements is NOT true about continuous probability distributions?
A)The probability of any event is the area under the density curve over the range of values that make up the event.
B)The total area under the density curve must be exactly 1.
C)If X is a continuous random variable taking values between 0 and 500, then P(X > 200) = P(X ≥ 200).
D)There are no disjoint events in continuous probability models.
A)The probability of any event is the area under the density curve over the range of values that make up the event.
B)The total area under the density curve must be exactly 1.
C)If X is a continuous random variable taking values between 0 and 500, then P(X > 200) = P(X ≥ 200).
D)There are no disjoint events in continuous probability models.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
44
If X is a continuous uniform random variable taking values between 0 and 10, then the value of the probability P(X ≤ 4.3) is
A)Slightly smaller than the value of P(X < 4.3).
B)Exactly the same as the value of P(X < 4.3).
C)Slightly larger than the value of P(X < 4.3).
D)Possibly smaller or larger than the value of P(X < 4.3).
A)Slightly smaller than the value of P(X < 4.3).
B)Exactly the same as the value of P(X < 4.3).
C)Slightly larger than the value of P(X < 4.3).
D)Possibly smaller or larger than the value of P(X < 4.3).

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
45
A probability can be called a risk when it applies to an undesirable outcome.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
46
An odds is the ratio of the probability of an outcome over the probability of that outcome not
occurring.
occurring.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
47
All human blood can be typed as either O, A, B, or AB. The distribution of the types varies a bit with race. Choose an African American person at random. Here are the approximate probabilities that the person you choose will have blood type O, B, or AB:
?
?
What is the probability that the person chosen has blood type A?
A)0.04
B)0.25
C)0.27
D)Impossible to determine from the information given
?
?
What is the probability that the person chosen has blood type A?
A)0.04
B)0.25
C)0.27
D)Impossible to determine from the information given

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
48
All human blood can be typed as either O, A, B, or AB. The distribution of the types varies a bit with race. Choose an African American person at random. Here are the approximate probabilities that the person you choose will have blood type O, B, or AB:
?
What is the probability that the person chosen has a blood type other than O?
A)0.25
B)0.50
C)0.75
D)1.00
?
What is the probability that the person chosen has a blood type other than O?
A)0.25
B)0.50
C)0.75
D)1.00

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
49
All human blood can be typed as either O, A, B, or AB. The distribution of the types varies a bit with race. Choose an African American person at random. Here are the approximate probabilities that the person you choose will have blood type O, B, or AB:
?
?
Some people consider having type AB blood to be an undesirable outcome because it may be difficult to find matching donors. What is the risk of having type AB?
A)0.05
B)0.95
C)1.05
D)20.0
?
?
Some people consider having type AB blood to be an undesirable outcome because it may be difficult to find matching donors. What is the risk of having type AB?
A)0.05
B)0.95
C)1.05
D)20.0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
50
All human blood can be typed as either O, A, B, or AB. The distribution of the types varies a bit with race. Choose an African American person at random. Here are the approximate probabilities that the person you choose will have blood type O, B, or AB:
?
?
Considering having type AB blood to be an undesirable outcome, what are the odds of having type AB blood?
A)0.050
B)0.053
C)0.950
D)19.0
?
?
Considering having type AB blood to be an undesirable outcome, what are the odds of having type AB blood?
A)0.050
B)0.053
C)0.950
D)19.0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
51
According to the Centers for Disease Control and Prevention, as much as 20% of the U.S. population gets the flu each year. In light of this probability, what are the odds of catching the influenza virus?
A)0.20
B)0.25
C)0.80
D)4.00
A)0.20
B)0.25
C)0.80
D)4.00

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
52
Many health professionals believe that attention disorders such as ADD and ADHD are being over-diagnosed. It is predicted that 60% of the diagnoses are incorrect. What are the odds of a diagnosis being incorrect?
A)0.40
B)0.60
C)0.67
D)1.50
A)0.40
B)0.60
C)0.67
D)1.50

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
53
A recent nationwide study of myopia (nearsightedness) found that 38.1% of Americans age 18 to 24 suffer from myopia. What is the probability that a randomly chosen American between the ages of 18 and 24 does NOT have myopia?
A)-0.381
B)0.381
C)0.616
D)0.619
A)-0.381
B)0.381
C)0.616
D)0.619

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
54
A recent nationwide study of myopia (nearsightedness) found that 38.1% of Americans age 18 to 24 suffer from myopia. What are the odds of myopia in the 18- to 24-year-old American population?
A)0.381
B)0.616
C)1.616
D)2.625
A)0.381
B)0.616
C)1.616
D)2.625

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
55
A recent nationwide study of myopia (nearsightedness) found that 38.1% of Americans age 18 to 24 suffer from myopia. What is the risk of myopia in the 18- to 24-year-old American population?
A)0.381
B)0.616
C)1.616
D)2.625
A)0.381
B)0.616
C)1.616
D)2.625

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
56
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among American women age 20 to 24 is 2791.5 per 100,000. What is the probability that a randomly chosen American woman between the ages of 20 and 24 does NOT have a Chlamydia infection?
A)0.0279
B)0.2792
C)0.7208
D)0.9721
A)0.0279
B)0.2792
C)0.7208
D)0.9721

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
57
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among American women age 20 to 24 is 2791.5 per 100,000. What is the approximate risk of a Chlamydia infection in a 20- to 24-year-old U.S. female?
A)0.0279
B)0.0287
C)0.2792
D)0.2872
A)0.0279
B)0.0287
C)0.2792
D)0.2872

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
58
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among American women age 20 to 24 is 2791.5 per 100,000. What are the approximate odds of a Chlamydia infection in the 20- to 24-year-old U.S. female population?
A)0.0279
B)0.0287
C)0.2792
D)0.2872
A)0.0279
B)0.0287
C)0.2792
D)0.2872

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck


