Deck 9: Independence and Conditional Probabilities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 9: Independence and Conditional Probabilities
1
Disjoint events are independent.
False
2
Gallup reports that 30% of American adults have high blood pressure. A medical office selects at random two unrelated medical records from the practice's adult patients.
What is the probability that both patients have high blood pressure?
A)0.09
B)0.21
C)0.60
D)0.30
What is the probability that both patients have high blood pressure?
A)0.09
B)0.21
C)0.60
D)0.30
A
3
Gallup reports that 30% of American adults have high blood pressure. A medical office selects at random two unrelated medical records from the practice's adult patients.
What is the probability that at least 1 patient has high blood pressure?
A)0.30
B)0.39
C)0.49
D)0.51
What is the probability that at least 1 patient has high blood pressure?
A)0.30
B)0.39
C)0.49
D)0.51
D
4
For a particular species of wolf, 55% are female, 20% hunt in medium-sized packs, and 15% are both female and hunt in medium-sized packs.
What is the percent of wolves that are female but do not hunt in medium-sized packs?
A)5%
B)35%
C)40%
D)55%
What is the percent of wolves that are female but do not hunt in medium-sized packs?
A)5%
B)35%
C)40%
D)55%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
For a particular species of wolf, 55% are female, 20% hunt in medium-sized packs, and 15% are both female and hunt in medium-sized packs.
What is the percent of wolves that are neither female nor hunt in medium-sized packs?
A)20%
B)40%
C)45%
D)80%
What is the percent of wolves that are neither female nor hunt in medium-sized packs?
A)20%
B)40%
C)45%
D)80%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
For a particular species of wolf, 55% are female, 20% hunt in medium-sized packs, and 15% are both female and hunt in medium-sized packs.
What is the percent of wolves that are female but do not hunt in medium-sized packs or that are not female but hunt in medium-sized packs?
A)0%
B)15%
C)30%
D)45%
What is the percent of wolves that are female but do not hunt in medium-sized packs or that are not female but hunt in medium-sized packs?
A)0%
B)15%
C)30%
D)45%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
For a particular species of wolf, 55% are female, 20% hunt in medium-sized packs, and 15% are both female and hunt in medium-sized packs.
What is the probability of selecting a wolf that is female, given that it hunts in a medium-sized pack?
A)0.15
B)0.25
C)0.55
D)0.75
What is the probability of selecting a wolf that is female, given that it hunts in a medium-sized pack?
A)0.15
B)0.25
C)0.55
D)0.75

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
A recent nationwide study of myopia (nearsightedness) found that 38.1% of U.S. adults ages 18 to 24 suffer from myopia. Consider two young adults between the ages of 18 and 24, chosen randomly and independently.
What is the probability that both individuals have myopia?
A)0.145
B)0.381
C)0.617
D)0.762
What is the probability that both individuals have myopia?
A)0.145
B)0.381
C)0.617
D)0.762

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
A recent nationwide study of myopia (nearsightedness) found that 38.1% of U.S. adults ages 18 to 24 suffer from myopia. Consider two young adults between the ages of 18 and 24, chosen randomly and independently.
What is the probability that neither of them has myopia?
A)0.238
B)0.383
C)0.619
D)0.855
What is the probability that neither of them has myopia?
A)0.238
B)0.383
C)0.619
D)0.855

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
Event A occurs with probability 0.1. Event B occurs with probability 0.6. If A and B are independent, then which of the following probabilities is correct?
A) P(A and B) = 0.06
B. P(A or B) = 0.70
C. P(A and B) = 0.70
D)P(A or B) = 0.06
A) P(A and B) = 0.06
B. P(A or B) = 0.70
C. P(A and B) = 0.70
D)P(A or B) = 0.06

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among U.S. women ages 20 to 24 is 2791.5 per 100,000. Take a random sample of three U.S. women in this age group.
What is the probability that all three women have a Chlamydia infection?
A)Nearly 0
B)0.028
C)0.084
D)0.837
What is the probability that all three women have a Chlamydia infection?
A)Nearly 0
B)0.028
C)0.084
D)0.837

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among U.S. women ages 20 to 24 is 2791.5 per 100,000. Take a random sample of three U.S. women in this age group.
What is the probability that none of the women has a Chlamydia infection?
A)0.084
B)0.919
C)0.972
D)Nearly 1
What is the probability that none of the women has a Chlamydia infection?
A)0.084
B)0.919
C)0.972
D)Nearly 1

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
The Centers for Disease Control and Prevention reports that the rate of Chlamydia infections among U.S. women ages 20 to 24 is 2791.5 per 100,000. Take a random sample of three U.S. women in this age group.
What is the probability that at least one of the women has a Chlamydia infection?
A)0.028
B)0.081
C)0.837
D)Nearly 1
What is the probability that at least one of the women has a Chlamydia infection?
A)0.028
B)0.081
C)0.837
D)Nearly 1

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
A researcher cross-classified 386 trout into groups based on their species (all were in genus Salmo) and gender:
?
?
A trout is to be selected at random. What is the probability that the selected trout is a flathead trout?
A)0.1451
B)0.1762
C)0.3212
D)0.3394
?
?
A trout is to be selected at random. What is the probability that the selected trout is a flathead trout?
A)0.1451
B)0.1762
C)0.3212
D)0.3394

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
A researcher cross-classified 386 trout into groups based on their species (all were in genus Salmo) and gender:
?
?
A trout is to be selected at random. What is the probability that the selected trout is a male flathead trout?
A)0.1451
B)0.1762
C)0.1036
D)0.6788
?
?
A trout is to be selected at random. What is the probability that the selected trout is a male flathead trout?
A)0.1451
B)0.1762
C)0.1036
D)0.6788

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
A researcher cross-classified 386 trout into groups based on their species (all were in genus Salmo) and gender:
?
?
A trout is to be selected at random. Given that the selected trout is male, what is the conditional probability that it is a Sevan trout?
A)0.0776
B)0.1717
C)0.3665
D)0.4516
?
?
A trout is to be selected at random. Given that the selected trout is male, what is the conditional probability that it is a Sevan trout?
A)0.0776
B)0.1717
C)0.3665
D)0.4516

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
Event A occurs with probability 0.3, and event B occurs with probability 0.4. If A and B are independent, what may we conclude about the relationship between events A and B?
A) P(A and B) = 0.12
B. P(A|B) = 0.3
C. P(B|A) = 0.4
D)All of these options are correct.
A) P(A and B) = 0.12
B. P(A|B) = 0.3
C. P(B|A) = 0.4
D)All of these options are correct.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Two-thirds of patients in a drug trial suffered from severe migraines as a side effect. Another side effect was impaired vision, with 25% of all patients having no impairment, 50% having some impairment, and 25% having severe impairment. Based on these probabilities, which of the following would be the correct tree diagram?
A)
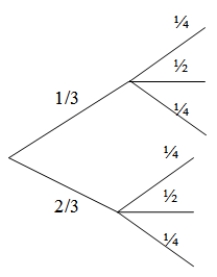
B)
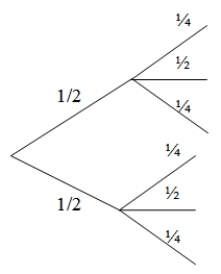
C)Both A and B are correct.
D)Neither A nor B is correct.
A)

B)

C)Both A and B are correct.
D)Neither A nor B is correct.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
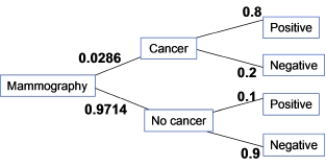
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
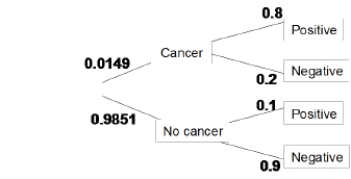 A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 40s taking a screening mammography receive a true positive?
A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 40s taking a screening mammography receive a true positive?
A)80%
B)11%
C)10%
D)1%
 A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 40s taking a screening mammography receive a true positive?
A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 40s taking a screening mammography receive a true positive?A)80%
B)11%
C)10%
D)1%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
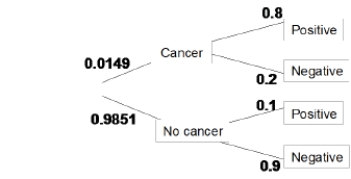 A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 40s taking a screening mammography receive a false positive?
A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 40s taking a screening mammography receive a false positive?
A)80%
B)11%
C)10%
D)1%
 A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 40s taking a screening mammography receive a false positive?
A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 40s taking a screening mammography receive a false positive?A)80%
B)11%
C)10%
D)1%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
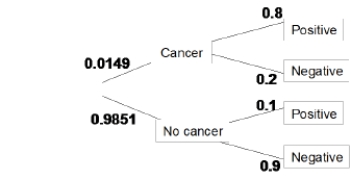 What percent of women in their 40s taking a screening mammography receive a positive test result?
What percent of women in their 40s taking a screening mammography receive a positive test result?
A)80%
B)11%
C)10%
D)1%
 What percent of women in their 40s taking a screening mammography receive a positive test result?
What percent of women in their 40s taking a screening mammography receive a positive test result?A)80%
B)11%
C)10%
D)1%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
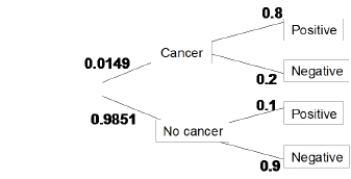 A false negative happens when someone getting a mammography does have cancer and receives a negative test. What percent of women in their 40s taking a screening mammography receive a false negative?
A false negative happens when someone getting a mammography does have cancer and receives a negative test. What percent of women in their 40s taking a screening mammography receive a false negative?
A)80%
B)11%
C)1.1%
D)0.3%
 A false negative happens when someone getting a mammography does have cancer and receives a negative test. What percent of women in their 40s taking a screening mammography receive a false negative?
A false negative happens when someone getting a mammography does have cancer and receives a negative test. What percent of women in their 40s taking a screening mammography receive a false negative?A)80%
B)11%
C)1.1%
D)0.3%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
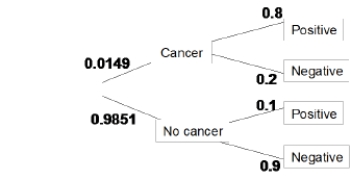 If a randomly chosen woman in her 40s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
If a randomly chosen woman in her 40s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
A)0.012
B)0.108
C)0.500
D)0.800
 If a randomly chosen woman in her 40s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
If a randomly chosen woman in her 40s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?A)0.012
B)0.108
C)0.500
D)0.800

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
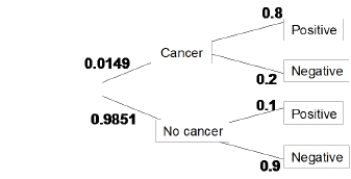 The specificity of a diagnosis test is its ability to appropriately give a negative result when a person tested doesn't have the disease, P(Negative test | No cancer). What is the specificity of mammography?
The specificity of a diagnosis test is its ability to appropriately give a negative result when a person tested doesn't have the disease, P(Negative test | No cancer). What is the specificity of mammography?
A)0.90
B)0.89
C)0.80
D)0.20
 The specificity of a diagnosis test is its ability to appropriately give a negative result when a person tested doesn't have the disease, P(Negative test | No cancer). What is the specificity of mammography?
The specificity of a diagnosis test is its ability to appropriately give a negative result when a person tested doesn't have the disease, P(Negative test | No cancer). What is the specificity of mammography?A)0.90
B)0.89
C)0.80
D)0.20

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 40s who takes a mammography to screen for breast cancer:
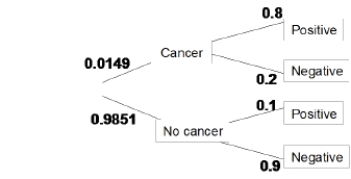 The sensitivity of a diagnosis test is its ability to appropriately give a positive result when a person tested has the disease, P(Positive test | Cancer). What is the sensitivity of mammography?
The sensitivity of a diagnosis test is its ability to appropriately give a positive result when a person tested has the disease, P(Positive test | Cancer). What is the sensitivity of mammography?
A)0.90
B)0.81
C)0.80
D)0.10
 The sensitivity of a diagnosis test is its ability to appropriately give a positive result when a person tested has the disease, P(Positive test | Cancer). What is the sensitivity of mammography?
The sensitivity of a diagnosis test is its ability to appropriately give a positive result when a person tested has the disease, P(Positive test | Cancer). What is the sensitivity of mammography?A)0.90
B)0.81
C)0.80
D)0.10

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 50s who takes a mammography to screen for breast cancer:
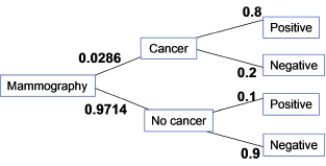 A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 50s taking a screening mammography receive a true positive?
A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 50s taking a screening mammography receive a true positive?
A)80%
B)50%
C)3%
D)2%
 A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 50s taking a screening mammography receive a true positive?
A true positive happens when someone getting a mammography has cancer and receives a positive test result. What percent of women in their 50s taking a screening mammography receive a true positive?A)80%
B)50%
C)3%
D)2%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 50s who takes a mammography to screen for breast cancer:
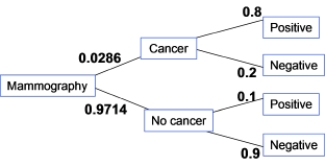 A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 50s taking a screening mammography receive a false positive?
A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 50s taking a screening mammography receive a false positive?
A)50%
B)16%
C)10%
D)2%
 A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 50s taking a screening mammography receive a false positive?
A false positive happens when someone getting a mammography does not have cancer and receives a positive test. What percent of women in their 50s taking a screening mammography receive a false positive?A)50%
B)16%
C)10%
D)2%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 50s who takes a mammography to screen for breast cancer:
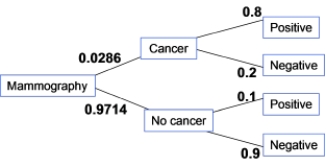 What percent of women in their 50s taking a screening mammography receive a positive test result?
What percent of women in their 50s taking a screening mammography receive a positive test result?
A)80%
B)12%
C)2%
D)3%
 What percent of women in their 50s taking a screening mammography receive a positive test result?
What percent of women in their 50s taking a screening mammography receive a positive test result?A)80%
B)12%
C)2%
D)3%

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 50s who takes a mammography to screen for breast cancer:
 If a randomly chosen woman in her 50s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
If a randomly chosen woman in her 50s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
A)0.03
B)0.19
C)0.50
D)0.80
 If a randomly chosen woman in her 50s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?
If a randomly chosen woman in her 50s taking the mammography screening test gets a positive test result, the probability that she indeed has breast cancer is the positive predicted value, PPV = P(Cancer | Positive test). What is the PPV for this age group?A)0.03
B)0.19
C)0.50
D)0.80

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
The incidence of breast cancer varies depending on a woman's age. The National Cancer Institute gives the following probabilities for a randomly chosen woman in her 50s who takes a mammography to screen for breast cancer:
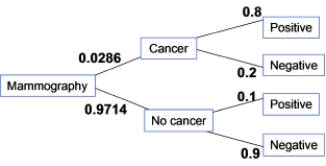 The sensitivity of a screening test is the ability of the test to appropriately give a positive result when the person tested has a given disease. Which of the following is the correct notation for the sensitivity of a screening test?
The sensitivity of a screening test is the ability of the test to appropriately give a positive result when the person tested has a given disease. Which of the following is the correct notation for the sensitivity of a screening test?
A)P(Positive test | Disease)
B)P(Disease | Positive test)
C)P(Disease and Positive test)
D)P(Positive test or Disease)
 The sensitivity of a screening test is the ability of the test to appropriately give a positive result when the person tested has a given disease. Which of the following is the correct notation for the sensitivity of a screening test?
The sensitivity of a screening test is the ability of the test to appropriately give a positive result when the person tested has a given disease. Which of the following is the correct notation for the sensitivity of a screening test?A)P(Positive test | Disease)
B)P(Disease | Positive test)
C)P(Disease and Positive test)
D)P(Positive test or Disease)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
What is the probability that an adult has a high BMI?
A)0.570
B)0.343
C)0.363
D)0.657
?
?
What is the probability that an adult has a high BMI?
A)0.570
B)0.343
C)0.363
D)0.657

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
What is the probability that an adult lives in a high-income country and has a high BMI?
A)0.125
B)0.570
C)0.218
D)0.363
?
?
What is the probability that an adult lives in a high-income country and has a high BMI?
A)0.125
B)0.570
C)0.218
D)0.363

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
What is the probability that an adult lives in a high-income country, given that the adult has a high BMI?
A)0.125
B)0.570
C)0.218
D)0.363
?
?
What is the probability that an adult lives in a high-income country, given that the adult has a high BMI?
A)0.125
B)0.570
C)0.218
D)0.363

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
What is the probability that an adult has a high BMI, given that the adult lives in a high-income country?
A)0.570
B)0.343
C)0.363
D)0.657
?
?
What is the probability that an adult has a high BMI, given that the adult lives in a high-income country?
A)0.570
B)0.343
C)0.363
D)0.657

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
What is the probability, P(high BMI | low-income country)?
A)0.014
B)0.042
C)0.150
D)0.176
?
?
What is the probability, P(high BMI | low-income country)?
A)0.014
B)0.042
C)0.150
D)0.176

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
Obesity is a growing public health concern worldwide. Adults with a body mass index (BMI) of 25 or greater are considered overweight or obese. The following table shows the number of adults (in millions) who are overweight or obese in countries with different income levels, based on data from the World Health Organization and the United Nations:
?
?
Which of the following options correctly describes country income level and BMI type?
A)Disjoint and independent
B)Disjoint but not independent
C)Independent but not disjoint
D)Not disjoint and not independent
?
?
Which of the following options correctly describes country income level and BMI type?
A)Disjoint and independent
B)Disjoint but not independent
C)Independent but not disjoint
D)Not disjoint and not independent

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
During winter, red foxes hunt small rodents by jumping into thick snow cover, without any visual clue. Researchers examined the compass direction of hundreds of such jumps. They found that 73% of jumps in the northeast direction were successful, compared with 60% of jumps in the southwest direction and only 18% of jumps in all other directions.
The value 73%, or 0.73, corresponds to which of the following probabilities?
A)P(successful jump | northeast direction)
B)P(northeast direction | successful jump)
C)P(successful jump and northeast direction)
D)P(successful jump or northeast direction)
The value 73%, or 0.73, corresponds to which of the following probabilities?
A)P(successful jump | northeast direction)
B)P(northeast direction | successful jump)
C)P(successful jump and northeast direction)
D)P(successful jump or northeast direction)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
During winter, red foxes hunt small rodents by jumping into thick snow cover, without any visual clue. Researchers examined the compass direction of hundreds of such jumps. They found that 73% of jumps in the northeast direction were successful, compared with 60% of jumps in the southwest direction and only 18% of jumps in all other directions.
Jumping direction and jump outcome are independent.
Jumping direction and jump outcome are independent.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


