Deck 27: Quantifying Uncertainty
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/39
Play
Full screen (f)
Deck 27: Quantifying Uncertainty
1
Why isn't the following statement a correct use of the word "probably"?
Last year, a good player probably scored four touchdowns in some game.
Last year, a good player probably scored four touchdowns in some game.
The statement refers to something that occurred (or did not occur) in the past.
2
Why isn't the following statement a correct use of the word "probably"?
Since the new arena opened, some event has probably been sold out.
Since the new arena opened, some event has probably been sold out.
The statement refers to something that occurred (or did not occur) in the past.
3
A bag has only red balls and green balls. The experiment is to draw one ball from the bag without looking. What does it mean to say, "The probability of getting a green ball is 40%"?
After many, many trials of the experiment, about 40% of the draws will give a green ball.
4
A bag has only blue balls and green balls. The experiment is to draw one ball from the bag without looking. What does it mean to say, "The probability of getting a green ball is 70%"?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose you have a brand new quarter. What does it mean to say, "The probability of getting heads when I toss the quarter is 50%"?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
6
What does it mean to say, "The probability of X is 0.8"?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
7
"In situation X, the probability of Y happening is 
." What does that mean?

." What does that mean?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
8
Fix the following statement so that it clearly describes a probabilistic situation.
Jane Smith probably had unusually bad luck last Friday.
Jane Smith probably had unusually bad luck last Friday.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
9
"You wonder what the chances were that the team's record would be five wins and one loss at this time last year" is a probabilistic situation.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
10
An event that CANNOT happen has a negative probability.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
11
If Y is impossible, the probability of not Y is one.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
12
The sum of the probabilities of all the outcomes of an experiment must be one.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
13
If a fair die is rolled once, the probability that you get a four, given that the die comes up an even number, is one-third.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
14
If you flip a fair coin 20 times, you will always get 10 tails.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
15
If you flip a fair coin 2000 times, you will always get 1000 heads.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
16
A) The theoretical probability of getting red for the spinner below is ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ. (The spinner is a regular pentagon.) 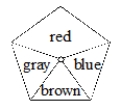
B) What does your answer in part A mean?
C) Tell how you would find the experimental probability for getting red for the spinner above if you wished to check your theoretical probability.

B) What does your answer in part A mean?
C) Tell how you would find the experimental probability for getting red for the spinner above if you wished to check your theoretical probability.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
17
A) The theoretical probability of getting red for the spinner below isـــــــــــــــــــــــــــــــــــــــــــــــ. (The spinner is a regular hexagon.) 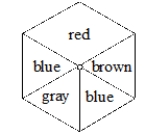
B) What does your answer in part A mean?
C) Tell how you would find the experimental probability for getting red for the spinner above if you wished to check your theoretical probability.

B) What does your answer in part A mean?
C) Tell how you would find the experimental probability for getting red for the spinner above if you wished to check your theoretical probability.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
18
In a particular experiment with only three outcomes, X, Y, and Z, the probability of X is and the probability of Y is . What is the probability of Z?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
19
"With our spinner, our group got probability of red = , probability of green = , and probability of yellow = ." What do you know without seeing the spinner?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
20
Experiment: Spin the spinner below twice, recording the color each time. 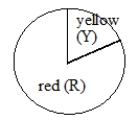
A) What outcome(s) is/are in the event "get different colors"? (Not the whole sample space, just the event.)
B) How would you determine the experimental probability of the event in part A? (Give a complete explanation, not just part of one.)

A) What outcome(s) is/are in the event "get different colors"? (Not the whole sample space, just the event.)
B) How would you determine the experimental probability of the event in part A? (Give a complete explanation, not just part of one.)

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
21
Experiment: Spin each of the two spinners below and record the color on each. 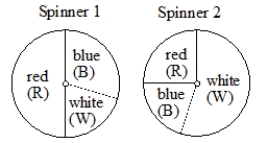
A) Give the sample space for the experiment.
B) Describe an event for the experiment above, and tell how one would determine the experimental probability for the event.

A) Give the sample space for the experiment.
B) Describe an event for the experiment above, and tell how one would determine the experimental probability for the event.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
22
In an experiment with two outcomes, each outcome must have probability 50%.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
23
For a three-color spinner with P(red) = and P(white) = , P(blue) could be .

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
24
The theoretical probability and the experimental probability of an event will be the same.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
25
In an experiment with four outcomes, P, Q, R, and S, the probability of P is , the probability of Q is , and the probabilities of R and S are equal to each other. What is the probability of S?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
26
Design a simulation for a spinner that would allow a simulation of a birth happening during any of the 12 months of the year with equal probabilities. Describe how you would carry out the simulation.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
27
Design an experiment based on drawing balls from a bag that would allow for the simulation of a success (getting well) for a sick person undergoing a treatment, with probability of success 0.6.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
28
You give a child the choice of drawing from two bags of balls. The child wins if he/she draws a red ball. Bag 1 has four red balls and seven green balls; bag 2 has two red balls and three green balls. Which bag gives the child a better chance of winning (or are the chances the same)? Please explain.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
29
Simulating an experiment with randomly generated numbers gives experimental probabilities.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
30
You may wish to use a table of randomly generated numbers efficiently to simulate this experiment.
Experiment: Draw a ball from a bag that has 13 black balls (B), 5 red balls (R), and 2 green balls (G), and note its color.
A) Tell what your code would be if you use two-digit random numbers. Use an efficient code, omitting as few numbers as you can.
00 01 02 03 …………………………………………………… 97 98 99
B) Use the following randomly selected digits to simulate the experiment above 15 times.
10394 8854 96029 711517 87601 71480 49210 81314 84069 64343 65909 23870
C) What is the theoretical probability of getting a red ball?
D) What is the probability of getting a red ball from your simulation in part B?
E) Explain the difference between the answer in part C and the answer in part D.
Experiment: Draw a ball from a bag that has 13 black balls (B), 5 red balls (R), and 2 green balls (G), and note its color.
A) Tell what your code would be if you use two-digit random numbers. Use an efficient code, omitting as few numbers as you can.
00 01 02 03 …………………………………………………… 97 98 99
B) Use the following randomly selected digits to simulate the experiment above 15 times.
10394 8854 96029 711517 87601 71480 49210 81314 84069 64343 65909 23870
C) What is the theoretical probability of getting a red ball?
D) What is the probability of getting a red ball from your simulation in part B?
E) Explain the difference between the answer in part C and the answer in part D.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
31
You may wish to use randomly selected digits efficiently to simulate this experiment.
Experiment: Draw a ball from a bag that has 11 black balls (B), 5 red balls (R), and 4 green balls (G), and note its color.
A) Tell what your code would be if you use two-digit numbers. Use an efficient code, omitting as few numbers as you can.
00 01 02 03 …………………………………………………… 97 98 99
B) Use the following from our table of randomly selected digits to simulate the experiment above 15 times efficiently.
11517 87601 71480 49210 81314 84069 64343 65909 23870 10394 8854 96029
C) What is the theoretical probability of getting a green ball?
D) What is the probability of getting a green ball from your simulation in part B?
E) Explain the difference between the answer in part C and the answer in part D.
Experiment: Draw a ball from a bag that has 11 black balls (B), 5 red balls (R), and 4 green balls (G), and note its color.
A) Tell what your code would be if you use two-digit numbers. Use an efficient code, omitting as few numbers as you can.
00 01 02 03 …………………………………………………… 97 98 99
B) Use the following from our table of randomly selected digits to simulate the experiment above 15 times efficiently.
11517 87601 71480 49210 81314 84069 64343 65909 23870 10394 8854 96029
C) What is the theoretical probability of getting a green ball?
D) What is the probability of getting a green ball from your simulation in part B?
E) Explain the difference between the answer in part C and the answer in part D.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
32
One basketball player hits 46% of her shots.
A) Give a code for hits and a code for misses so that one could use the table of randomly selected digits to simulate shots by the player.
B) If you use your code two times to simulate 300 shots each time, will you get the same results both times? Explain why/why not.
A) Give a code for hits and a code for misses so that one could use the table of randomly selected digits to simulate shots by the player.
B) If you use your code two times to simulate 300 shots each time, will you get the same results both times? Explain why/why not.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
33
Ten percent of the time a student comes to my office, he or she leaves something behind. Estimate the probability, using a simulation model and the two-line random number table given, that exactly one out of the next four students will leave something behind. (Use 20 samples.) Show how you came to your answer.
13366527640249714202741725877065348241154427796735
96734100241534687634091232686745732531809874574312
13366527640249714202741725877065348241154427796735
96734100241534687634091232686745732531809874574312

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
34
A) Design a table of randomly selected digits simulation for the following experiment.
Spin a spinner that is red,
red,  green, and the rest white, and notice the color.
green, and the rest white, and notice the color.
B) Do your simulation 20 times. Record enough so that your work can be checked.
C) According to your simulation, what is the probability of green?
Spin a spinner that is
 red,
red,  green, and the rest white, and notice the color.
green, and the rest white, and notice the color. B) Do your simulation 20 times. Record enough so that your work can be checked.
C) According to your simulation, what is the probability of green?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
35
An experimental rocket will be launched. The launch has an 89% probability of success. With a table of randomly selected digits, what would be an efficient code for success and an efficient code for failure for simulating the launch?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
36
Simulating an experiment with software gives theoretical probabilities.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
37
Experiment: Toss four dishonest coins-penny, nickel, dime, quarter-with P(H) = 0.6 for each coin. A computer produced the table below for a simulation of the whole experiment 8000 times. 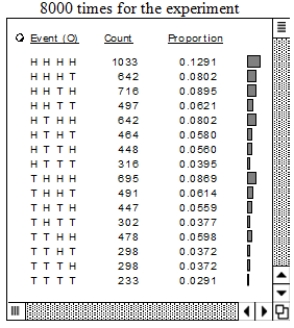
A) In the HHHH line (the first line in the body of the table), how did the computer calculate to get 0.1291?
B) What is the probability of at least one tail (T), according to this simulation?

A) In the HHHH line (the first line in the body of the table), how did the computer calculate to get 0.1291?
B) What is the probability of at least one tail (T), according to this simulation?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
38
Experiment: Toss four dishonest coins-penny, nickel, dime, quarter-with P(H) = 0.6 for each coin. A computer produced the table below for a simulation of the whole experiment 8000 times. 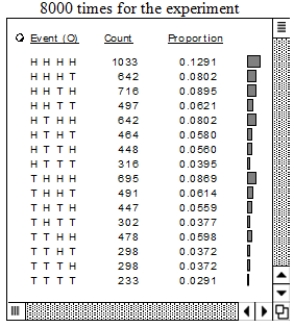
A) In the HHTT line (the fourth line in the body of the table), how did the computer calculate to get 0.0621?
B) What is the probability of at least one head (H), according to this simulation?

A) In the HHTT line (the fourth line in the body of the table), how did the computer calculate to get 0.0621?
B) What is the probability of at least one head (H), according to this simulation?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
39
The computer outputs below are for 3000 trials of spinning the spinners. Explain the differences in the outputs between the two spinners. (Event (O) means the outcomes are ordered.) 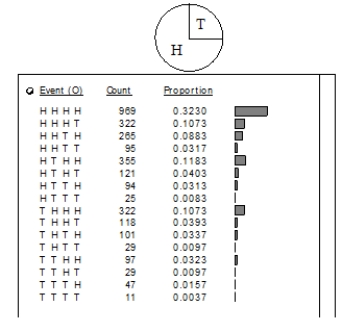
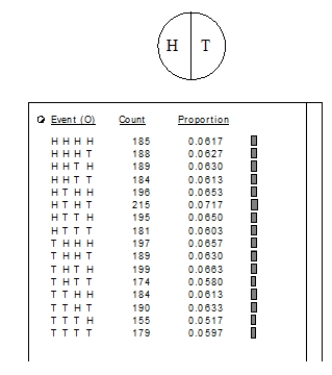



Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck


