Deck 16: Polygons
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Match between columns
Premises:
Every rectangle is a square.
Every rectangle is a square.
Every square is a quadrilateral.
Every square is a quadrilateral.
Responses:
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/74
Play
Full screen (f)
Deck 16: Polygons
1
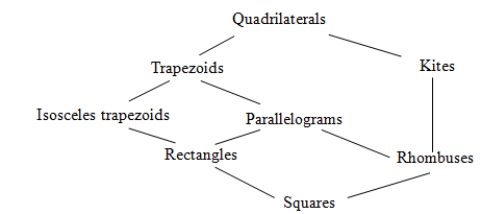
Draw a tree diagram showing the hierarchy of the following quadrilaterals: kites, trapezoids, parallelograms, squares, rhombuses, isosceles trapezoids, and rectangles. (Note: Use "quadrilaterals" at the top of your diagram.)
2
Sketch an example, if it is possible, of each shape described. If any are not possible tosketch, explain why.
A) an isosceles triangle that is not an acute triangle
B) a quadrilateral with two 90° angles that is not a rectangle (Be sure to mark the 90° angles.)
C) a kite that is also a rectangle
D) a triangular right prism (Show every hidden edge as a dashed segment.)
A) an isosceles triangle that is not an acute triangle
B) a quadrilateral with two 90° angles that is not a rectangle (Be sure to mark the 90° angles.)
C) a kite that is also a rectangle
D) a triangular right prism (Show every hidden edge as a dashed segment.)
A) a sketch of a right isosceles triangle or an obtuse isosceles triangle
B) a sketch of a trapezoid that is not isosceles (two right angles)
C) a sketch of a square
D) a sketch of a right prism with triangular bases or a right prism with right triangular bases (The latter is probably acceptable, unless you have emphasized the former.)
B) a sketch of a trapezoid that is not isosceles (two right angles)
C) a sketch of a square
D) a sketch of a right prism with triangular bases or a right prism with right triangular bases (The latter is probably acceptable, unless you have emphasized the former.)
3
For each shape, sketch an example if it is possible. If it is not possible, say so and explain why.
A) a trapezoid with exactly one right angle
B) a parallelogram that is an isosceles trapezoid
C) a pentagon with exactly one right angle
D) an isosceles obtuse triangle
E) a rhombus that is not a kite
A) a trapezoid with exactly one right angle
B) a parallelogram that is an isosceles trapezoid
C) a pentagon with exactly one right angle
D) an isosceles obtuse triangle
E) a rhombus that is not a kite
A) This is not possible because the parallel sides will force at least two right angles if there is one.
B) a sketch of any rectangle/square
C) a sketch with exactly one right angle and five sides
D) One example is a triangle with angles of 120°, 30°, and 30°.
E) This is not possible because every rhombus is a special kite.
B) a sketch of any rectangle/square
C) a sketch with exactly one right angle and five sides
D) One example is a triangle with angles of 120°, 30°, and 30°.
E) This is not possible because every rhombus is a special kite.
4
What is the sum of the measures of the exterior angles, one at each vertex, of every convex polygon? Explain your reasoning.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
5
Tell whether each statement is always true, sometimes true, or never true. Justify your choice.
A) The diagonals of a parallelogram bisect each other.
B) The diagonals of a kite bisect each other.
A) The diagonals of a parallelogram bisect each other.
B) The diagonals of a kite bisect each other.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
6
Indicate whether each statement is always true, sometimes true, or never true. Justify your choice.
A) A parallelogram is an isosceles trapezoid.
B) A square is a rhombus.
C) A scalene triangle is an acute triangle.
A) A parallelogram is an isosceles trapezoid.
B) A square is a rhombus.
C) A scalene triangle is an acute triangle.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the following definitions of a trapezoid.
Definition A: A quadrilateral with at least one pair of opposite sides parallel.
Definition B: A quadrilateral with exactly one pair of opposite sides parallel.
Is it possible to draw a figure that is a trapezoid according to definition A but not a trapezoid according to definition B? If yes, draw a figure that satisfies the conditions and explain why your figure satisfies those conditions. If no, explain why not.
Definition A: A quadrilateral with at least one pair of opposite sides parallel.
Definition B: A quadrilateral with exactly one pair of opposite sides parallel.
Is it possible to draw a figure that is a trapezoid according to definition A but not a trapezoid according to definition B? If yes, draw a figure that satisfies the conditions and explain why your figure satisfies those conditions. If no, explain why not.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
8
Every square is a special quadrilateral.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
9
Every rectangle is a parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
10
Every rhombus is a parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
11
Every rectangle is a special square.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
12
Every trapezoid is a special parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
13
Any fact that is true for every parallelogram is also true for every square.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
14
Any fact that is true for every rectangle is also true for every quadrilateral.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
15
Draw (if possible) an isosceles trapezoid with exactly one right angle. If it is not possible, explain why.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
16
Draw (if possible) a kite that does not have four congruent sides. If it is not possible, explain why.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
17
Give the best name (if the shape is possible) for the descriptions listed below. If the shape is not possible, explain why.
A) a kite that is also an isosceles trapezoid
B) a rhombus that is not equilateral
C) an equilateral (but not regular) isosceles trapezoid
A) a kite that is also an isosceles trapezoid
B) a rhombus that is not equilateral
C) an equilateral (but not regular) isosceles trapezoid

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
18
Every kite is also a parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
19
There are a total of 1175 diagonals in a 50-gon.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
20
It is possible to make a regular pyramid using an isosceles trapezoid as a base.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
21
A pentagonal pyramid has a total of five vertices.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
22
The lateral faces of a prism are always parallelogram regions.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
23
A rhombus is a kite.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
24
The interior angles of a trapezoid add up to 360°, but only 270° if it is an isosceles trapezoid.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
25
Give the best name for the following shapes.
A) a regular quadrilateral
B) an isosceles trapezoid with at least one right angle
A) a regular quadrilateral
B) an isosceles trapezoid with at least one right angle

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
26
If possible, sketch an example of each description. If it is not possible, explain why. Use tick marks and hidden edges and label equal angles to make your intent clear.
A) a trapezoid with exactly two right angles
B) a kite with equal diagonals
A) a trapezoid with exactly two right angles
B) a kite with equal diagonals

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
27
For the following conjecture, draw an example that supports the claim and also one that shows the claim is false.
"The diagonals of a parallelogram are equal."
"The diagonals of a parallelogram are equal."

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
28
Which shape will have ALL of the properties that every isosceles trapezoid has?
A) parallelogram
B) kite
C) rhombus
D) rectangle
A) parallelogram
B) kite
C) rhombus
D) rectangle

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
29
Why is it NOT safe to make a general conclusion based on a drawing?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
30
Why is a result from inductive reasoning NOT completely trustworthy?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
31
Put the following terms in the blanks below to show the relationship among them: isosceles trapezoid, parallelogram, quadrilateral, rectangle, and rhombus. 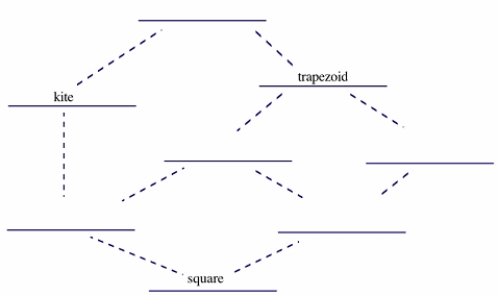


Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
32
Arrange (only) the following terms in a hierarchical diagram, with the most general at the top: kite, square, polygon, trapezoid, and rectangle.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
33
Complete the following statements.
A) The measure of EACH interior angle of a regular decagon is _____.
B) If an interior angle of a regular polygon is 175°, then the polygon has _____ sides.
C) The number of congruent sides on a scalene triangle is _____.
D) The number of diagonals in a 16-gon is _____.
A) The measure of EACH interior angle of a regular decagon is _____.
B) If an interior angle of a regular polygon is 175°, then the polygon has _____ sides.
C) The number of congruent sides on a scalene triangle is _____.
D) The number of diagonals in a 16-gon is _____.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
34
For each shape, sketch an example if it is possible. (Be sure to mark your picture to fit.) If it is impossible, say so and explain why or show a counterexample.
A) a parallelogram with exactly one right angle
B) an isosceles right triangle
C) a rectangle that is not a parallelogram
D) an equilateral quadrilateral that is not regular
E) a concave hexagon
A) a parallelogram with exactly one right angle
B) an isosceles right triangle
C) a rectangle that is not a parallelogram
D) an equilateral quadrilateral that is not regular
E) a concave hexagon

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
35
Match between columns
Premises:
Every rectangle is a square.
Every rectangle is a square.
Every square is a quadrilateral.
Every square is a quadrilateral.
Responses:
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False
True
False

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
36
A student states that a square cannot be a rhombus. What irrelevant characteristic(s) might she be assuming to be important? How would you help her to understand her error?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
37
How many diagonals does each of these shapes have?
A) a pentagon
B) a 103-gon
A) a pentagon
B) a 103-gon

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
38
The sizes of three interior angles of a quadrilateral are 65°, 35°, and 60°. What is the size of the fourth angle of the quadrilateral?
A) 20°
B) 100°
C) 160°
D) 200°
E) This quadrilateral is impossible.
A) 20°
B) 100°
C) 160°
D) 200°
E) This quadrilateral is impossible.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
39
An isosceles triangle has two angles that measure 100° and 40°. How large is the third angle?
A) 40°
B) 60°
C) 100°
D) 140°
E) More information is needed to answer the question.
A) 40°
B) 60°
C) 100°
D) 140°
E) More information is needed to answer the question.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
40
If a polygon is equiangular, then it must be:
A) equilateral.
B) regular.
C) a triangle.
D) equilateral and regular.
E) None of the answers is correct.
A) equilateral.
B) regular.
C) a triangle.
D) equilateral and regular.
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
41
An angle that is supplementary to an angle with size 70° has what size?
A) 20°
B) 70°
C) 90°
D) 110°
E) 180°
A) 20°
B) 70°
C) 90°
D) 110°
E) 180°

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
42
Find the number of degrees in each lettered angle. 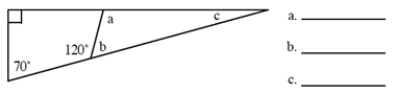


Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
43
The sum of the measures of all of the angles of a 17-gon is _____.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
44
Indicate whether each statement is always true, sometimes true, or never true. If the answer is sometimes true, then draw a picture of a shape that meets both requirements and a shape that meets only the first requirement.
A) A parallelogram is a rectangle.
B) A rectangle is a parallelogram.
C) A rhombus is a rectangle.
D) A prism is a pyramid.
A) A parallelogram is a rectangle.
B) A rectangle is a parallelogram.
C) A rhombus is a rectangle.
D) A prism is a pyramid.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
45
When asked to find the sum of the interior angles in a hexagon, a student writes the statement alongside the sketch below. Comment on whether the student's mathematical reasoning is correct or incorrect. If it is correct, explain how you know. If it is incorrect, explain what was incorrect about the student's thinking and what he/she would have to do to correct the error. 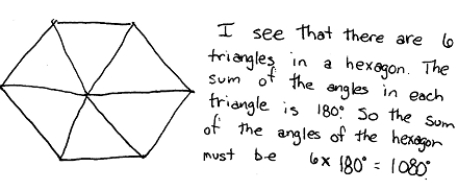


Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
46
Sketch an example of each description if it is possible. If any sketches are not possible, explain why.
A) an equilateral quadrilateral that is not equiangular (What is this shape usually called?)
B) an equilateral obtuse triangle
C) a pentagon with exactly three right angles
A) an equilateral quadrilateral that is not equiangular (What is this shape usually called?)
B) an equilateral obtuse triangle
C) a pentagon with exactly three right angles

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
47
Create a Venn diagram or a hierarchy diagram for only the following terms: quadrilateral, square, rectangle, polygon, and rhombi.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
48
A) How many different arrangements of three identical rhombi are possible in which each rhombus matches up edge to edge with at least one other rhombus? Two arrangements are considered the same if one of the arrangements can be flipped and/or rotated to obtain the other arrangement. Sketch all possible arrangements.
B) Explain a counting strategy you used to justify that you have found all the different arrangements.
B) Explain a counting strategy you used to justify that you have found all the different arrangements.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
49
Why is 10 called a triangular number?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
50
Sketch, if possible, an obtuse isosceles triangle that has an angle with 30°. If such a triangle exists, give the measures of the other angles. If such a triangle is impossible, explain why.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
51
State a fact that is true for all rhombi but not true for all kites.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
52
State a fact that is true for all rectangles but not true for all parallelograms.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
53
State two facts that are true for the diagonals of every rhombus.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
54
State two facts that are true for the diagonals of every rectangle.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
55
State two facts that are true for every parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
56
The diagonals of a parallelogram are equal.
A) always true
B) sometimes true
C) never true
A) always true
B) sometimes true
C) never true

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
57
A square is a rhombus.
A) always true
B) sometimes true
C) never true
A) always true
B) sometimes true
C) never true

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
58
The diagonals of every parallelogram:
A) bisect the angles of the parallelogram.
B) are parallel to each other.
C) are perpendicular to each other.
D) are equal in length.
E) None of the answers is correct.
A) bisect the angles of the parallelogram.
B) are parallel to each other.
C) are perpendicular to each other.
D) are equal in length.
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
59
Which statement is TRUE for every rhombus?
I. The diagonals of a rhombus must be equal.
II. The sides of a rhombus must be equal.
A) I only
B) II only
C) I and III
D) neither I nor II
I. The diagonals of a rhombus must be equal.
II. The sides of a rhombus must be equal.
A) I only
B) II only
C) I and III
D) neither I nor II

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
60
If IJKLMN is a regular polygon, then:
A) all the diagonals are equal in length.
B) IJKLMN has seven sides.
C) angle JKL has twice as many degrees as angle LMN.
D) drawing all the diagonals from K gives six triangles.
E) None of the answers is correct.
A) all the diagonals are equal in length.
B) IJKLMN has seven sides.
C) angle JKL has twice as many degrees as angle LMN.
D) drawing all the diagonals from K gives six triangles.
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
61
How are the diagonals of every rectangle related?
I. The diagonals are the same length.
II. The diagonals are perpendicular.
III. The diagonals bisect the angles of the rectangle.
A) I only
B) II only
C) III only
D) I and III only
E) None of the answers is correct.
I. The diagonals are the same length.
II. The diagonals are perpendicular.
III. The diagonals bisect the angles of the rectangle.
A) I only
B) II only
C) III only
D) I and III only
E) None of the answers is correct.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
62
Every square is a special quadrilateral.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
63
Every rectangle is a parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
64
Every rhombus is a parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
65
Every rectangle is a special square.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
66
Every trapezoid is a special parallelogram.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
67
Any fact that is true for every parallelogram is also true for every square.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
68
Any fact that is true for every rectangle is also true for every quadrilateral.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
69
What is the BEST name for every four-sided polygon with equal sides?
A) square
B) parallelogram
C) rectangle
D) rhombus
E) kite
A) square
B) parallelogram
C) rectangle
D) rhombus
E) kite

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
70
Fill in each blank with the BEST choice from the list of shapes A-E. You may re-use a choice.
_______has parallel lateral edges
_______a regular quadrilateral
_______has an equal number of faces and vertices
_______a polygon that is never a kite
_______possibility of all its faces being regular
is always a kite
_______has lateral faces that are triangular regions
has two bases
A) pyramid
B) non-square rectangle
C) parallelogram
D) square
E) oblique prism
_______has parallel lateral edges
_______a regular quadrilateral
_______has an equal number of faces and vertices
_______a polygon that is never a kite
_______possibility of all its faces being regular
is always a kite
_______has lateral faces that are triangular regions
has two bases
A) pyramid
B) non-square rectangle
C) parallelogram
D) square
E) oblique prism

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
71
Is it possible for the sum of the angles of a polygon to be 180,000°? Explain.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
72
What is the measure of one interior angle of a regular 18-gon?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
73
Find the measure of angle A of the triangle. 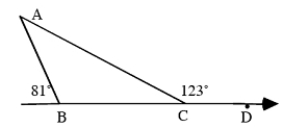
A) 156°
B) 24°
C) 57°
D) 20°
E) More information is needed to answer the question.

A) 156°
B) 24°
C) 57°
D) 20°
E) More information is needed to answer the question.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
74
Which, if either, of the following is IMPOSSIBLE for x, y, and z in the sketch below? (The drawing is not to scale.)
I. x = 100, y = 110, z = 150
II. x = 80, y = 130, z = 150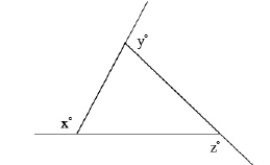
A) Only I is impossible.
B) Only II is impossible.
C) Both I and II are impossible.
D) Both I and II are possible.
I. x = 100, y = 110, z = 150
II. x = 80, y = 130, z = 150

A) Only I is impossible.
B) Only II is impossible.
C) Both I and II are impossible.
D) Both I and II are possible.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck


