Deck 15: Further Topics in Algebra and Change
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 15: Further Topics in Algebra and Change
1
Write an equation for the line that has slope 3 and passes through the point (2, 7). Simplify to the
form.
form.
2
Write an equation for the line that has slope 3 and passes through the point (9, 7). Simplify to the
form.
form.
(or )
3
Write an equation for the line that has slope
and passes through the point (2, 1). Simplify to the
form.
and passes through the point (2, 1). Simplify to the
form.
4
Write an equation for the line that has slope
and passes through the point (20, 10). Simplify to the
form.
and passes through the point (20, 10). Simplify to the
form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
Write an equation for the line that has slope
and passes through the point (12, 6). Simplify to the
form.
and passes through the point (12, 6). Simplify to the
form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
Write an equation for the line that has slope and passes through the point (4, ). Simplify to the
form.
form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
Write an equation for the line that passes through the points (1, 8) and (7, 44). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
Write an equation for the line that passes through the points (10, 5) and (3,
). Simplify to the form.
). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
Write an equation for the line that passes through the points (1, 9) and (4, 0). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
Write an equation for the line that passes through the points (2, 7) and (6, 13). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Write an equation for the line that passes through the points (6, ) and (1, ). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
Write an equation for the line that passes through the points (4, ) and ( , ). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
Write an equation for the line that is parallel to the line of and passes through the point (1, 16). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
Write an equation for the line that is parallel to the line of and passes through the point (4, 9). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
15
Write an equation for the line that is perpendicular to the line of and passes through the point (8, 4). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
Write an equation for the line that is perpendicular to the line of and passes through the point (15, 2). Simplify to the form.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
Wile E. was going back to his cave and spotted his cousin, waiting for him. So Wile E. started jogging toward his cave at a steady speed of 40 feet/second. After 3 seconds and while 120 feet from his cave, Wile E. sprained his ankle. How far was Wile E. from his cave when he spotted his cousin?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
Wile E. was at the top of a cliff when he spotted Road Runner at the bottom of the cliff. Wile E. jumped off the cliff, using an umbrella as a parachute to get a steady speed. After 2 minutes, Wile E. was 960 feet from the bottom of the cliff, and after 5 minutes, he was 480 feet from the bottom.
A) What was Wile E.'s speed going down?
B) What was the height of the cliff, top to bottom?
C) When did Wile E. reach the bottom of the cliff?
A) What was Wile E.'s speed going down?
B) What was the height of the cliff, top to bottom?
C) When did Wile E. reach the bottom of the cliff?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution 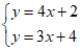
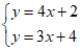

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. 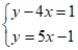
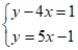

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. 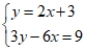
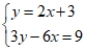

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
Use the substitution method to find a common solution to the given equations, if there is one, or state that there is no common solution. 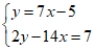
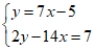

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution. 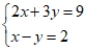
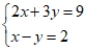

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution. 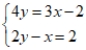
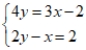

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution. 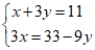
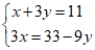

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
Use the addition/subtraction method to find a common solution to the given equations, if there is one, or state that there is no common solution. 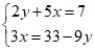
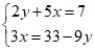

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
A) Give an equation that is dependent with 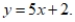
B) Give an equation that is inconsistent wit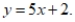
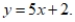
B) Give an equation that is inconsistent wit
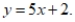

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
One building has parallel elevator shafts for a passenger elevator P and a freight elevator F. Assume that each elevator moves at (its) steady speed and can start and stop instantly. One time during a particular day, P and F start trips at the same time. After 2 minutes, P was 400 feet from the bottom of the shafts, heading down, and F was 120 feet from the bottom, heading up at a speed of 20 feet/minute. Four minutes after the start of the trip, P was 280 feet from the bottom of the shafts.
A) Write an equation describing the height h of elevator P (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
B) At what height did elevator P start the trip, and what was its speed?
C) Write an equation describing the height h of elevator F (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
D) When the trips started, where was elevator F?
E) When, if ever, were the two elevators at the same height above the bottom of the shafts? If they were at the same height, what was that height?
A) Write an equation describing the height h of elevator P (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
B) At what height did elevator P start the trip, and what was its speed?
C) Write an equation describing the height h of elevator F (in feet) above the bottom of the shafts, t minute(s) after the start of the trip.
D) When the trips started, where was elevator F?
E) When, if ever, were the two elevators at the same height above the bottom of the shafts? If they were at the same height, what was that height?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
You like to go to the neighborhood salad smorgasbord for a meal. The smorgasbord has a fixed charge for the salad makings but charges separately for drinks. When you had 2 sodas, you paid $11.45. When you had 4 sodas, you paid $13.95.
A) Write an equation that would enable you to tell the cost c (in dollars) for the salad makings and sodas d.
B) What does the slope of the equation tell you about this situation?
C) What is the cost for the salad alone?
A) Write an equation that would enable you to tell the cost c (in dollars) for the salad makings and sodas d.
B) What does the slope of the equation tell you about this situation?
C) What is the cost for the salad alone?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
Ordinarily, it takes Brother 20 minutes to go from home to school, and it takes Sister 16 minutes to go from home to school. Each child walks at a steady rate. Today, Brother left home at 8:00 AM and got a three-minute head start on Sister, who left at 8:03 AM.
A) Draw a graph to show the percent of the distance to school that Sister has covered versus the time. Label the graph S.
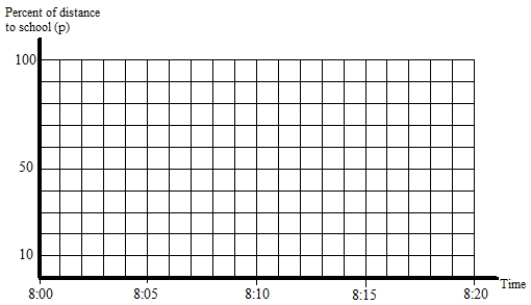
B) On the coordinate system above, draw a second graph to show the percent of the distance to school that Brother has covered. Label the graph B.
C) According to your graphs, will Sister catch up with Brother? If so, how do you know, and when does she catch up? If not, how do you know?
D) What is the slope of Brother's graph, and what does that slope mean in this situation?
A) Draw a graph to show the percent of the distance to school that Sister has covered versus the time. Label the graph S.

B) On the coordinate system above, draw a second graph to show the percent of the distance to school that Brother has covered. Label the graph B.
C) According to your graphs, will Sister catch up with Brother? If so, how do you know, and when does she catch up? If not, how do you know?
D) What is the slope of Brother's graph, and what does that slope mean in this situation?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
Ordinarily, it takes Brother 20 minutes to go from home to school, and it takes Sister 16 minutes to go from home to school. Today, Brother got a two-minute head start on Sister. 
A) Draw a graph to show the percent of the distance to school that Sister has covered versus the time that Sister travels. Label the graph S.
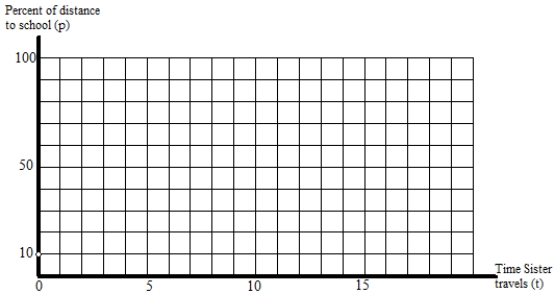
B) On the coordinate system above, draw a second graph B to show the percent of the distance to school that Brother has covered, using Sister's travel-time scale as the clock. One point, taking into account Brother's head start, is shown. (Be sure to notice that the horizontal axis scale is for Sister's travel time.)
C) According to your graphs, will Sister catch up with Brother? If so, how do you know, and when does she catch up? If not, how do you know?

A) Draw a graph to show the percent of the distance to school that Sister has covered versus the time that Sister travels. Label the graph S.

B) On the coordinate system above, draw a second graph B to show the percent of the distance to school that Brother has covered, using Sister's travel-time scale as the clock. One point, taking into account Brother's head start, is shown. (Be sure to notice that the horizontal axis scale is for Sister's travel time.)
C) According to your graphs, will Sister catch up with Brother? If so, how do you know, and when does she catch up? If not, how do you know?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the following problem with two different approaches. Label them A and B. Write enough to make it clear that your approaches are different.
Dylan and Eddie like to race each other. But Dylan is faster than Eddie. Dylan can run 50 yards/second, and Eddie can run only 40 yards/second. So Dylan gives Eddie a head start of 2 seconds. How far will the boys have to run when Dylan catches Eddie?
Dylan and Eddie like to race each other. But Dylan is faster than Eddie. Dylan can run 50 yards/second, and Eddie can run only 40 yards/second. So Dylan gives Eddie a head start of 2 seconds. How far will the boys have to run when Dylan catches Eddie?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
You and your roommates want to subscribe to a movie rental service. You have two choices: Movies-R-Us charges $15/month, plus $3.50 per movie rented, and See-It-Now charges $7.95/month, plus $5 per movie rented.
A) For each choice, write an equation giving the cost c for renting n movies a month.
B) Which choice should you make, under different scenarios? (For example, you watch lots of movies, you watch only occasionally, etc.) Give your reasoning, perhaps supporting your idea with a graph.
A) For each choice, write an equation giving the cost c for renting n movies a month.
B) Which choice should you make, under different scenarios? (For example, you watch lots of movies, you watch only occasionally, etc.) Give your reasoning, perhaps supporting your idea with a graph.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
You are on the committee planning your school's annual food fair, where parents provide food samples that people buy with food tickets. You are considering three plans for charges:
Highest entry, lowest ticket price entry, plus 504 for each food ticket
Middle entry, middle ticket price (MM): entry, plus for each food ticket
Low entry, highest ticket price : entry, plus for each food ticket Which plan do you think is best? Be sure to support your idea wit
equations, a graph, a table, or quantitative analysis.
Highest entry, lowest ticket price entry, plus 504 for each food ticket
Middle entry, middle ticket price (MM): entry, plus for each food ticket
Low entry, highest ticket price : entry, plus for each food ticket Which plan do you think is best? Be sure to support your idea wit
equations, a graph, a table, or quantitative analysis.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
Mr. Cool joins Rabbit and Turtle in an over-and-back race, 200 meters each way.
Rabbit: speed over = 50 meters/second; time back = 10 seconds
Mr. Cool: time over = 8 seconds; speed back = 40 meters/second
Turtle: the same speed both ways but rested for 5 seconds after the first 200 meters
A) Who finished first, Rabbit or Mr. Cool, and what was each one's time in seconds?
B) What was Rabbit's average speed for the race?
C) What was Turtle's speed when he was moving if Turtle tied Rabbit (remember that Turtle rested for 5 seconds)?
Rabbit: speed over = 50 meters/second; time back = 10 seconds
Mr. Cool: time over = 8 seconds; speed back = 40 meters/second
Turtle: the same speed both ways but rested for 5 seconds after the first 200 meters
A) Who finished first, Rabbit or Mr. Cool, and what was each one's time in seconds?
B) What was Rabbit's average speed for the race?
C) What was Turtle's speed when he was moving if Turtle tied Rabbit (remember that Turtle rested for 5 seconds)?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
Chicken joins Turtle and Rabbit in an over-and-back race, with known data as in the drawing below. 
A) Going the same speed over and back, Rabbit won the race. What was Rabbit's speed? Explain your thinking.
B) What was Chicken's average speed for the whole over-and-back trip? Show your work.

A) Going the same speed over and back, Rabbit won the race. What was Rabbit's speed? Explain your thinking.
B) What was Chicken's average speed for the whole over-and-back trip? Show your work.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
Wile E. joined Rabbit and Turtle in an over-and-back race, 200 meters each way. Show your work.
Rabbit: speed over = 20 meters/second; time back = 4 seconds
Wile E.: time over = 8 seconds; speed back = 40 meters/second
Turtle: the same speed both ways
A) Who of Rabbit and Wile E. finished first?
B) What was Turtle's speed, if he tied Rabbit?
C) Use one coordinate system to show qualitative speed versus time graphs for Rabbit's (mark with ____), Wile E.'s (mark with ......), and Turtle's (mark with x x x x) speeds over and back.
Rabbit: speed over = 20 meters/second; time back = 4 seconds
Wile E.: time over = 8 seconds; speed back = 40 meters/second
Turtle: the same speed both ways
A) Who of Rabbit and Wile E. finished first?
B) What was Turtle's speed, if he tied Rabbit?
C) Use one coordinate system to show qualitative speed versus time graphs for Rabbit's (mark with ____), Wile E.'s (mark with ......), and Turtle's (mark with x x x x) speeds over and back.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
A racing chicken and a fast squirrel join Turtle and Rabbit in an over-and-back race, with known data as in the drawing below. 
A) Going the same speed over and back, Rabbit just barely won the race. What was Rabbit's approximate speed? Explain your thinking.
B) Who came in second, third, and fourth? (Indicate ties, if any. No explanation is required.)
C) At the halfway mark of the race (300 feet), what was the order of the animals? (Indicate ties, if any. No explanation is required.)
D) What was Chicken's average speed over?

A) Going the same speed over and back, Rabbit just barely won the race. What was Rabbit's approximate speed? Explain your thinking.
B) Who came in second, third, and fourth? (Indicate ties, if any. No explanation is required.)
C) At the halfway mark of the race (300 feet), what was the order of the animals? (Indicate ties, if any. No explanation is required.)
D) What was Chicken's average speed over?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
A new "over" distance is set at 100 feet. Rabbit takes 5
seconds to go over and comes back at 40 feet/second. What should Turtle's speed be so that the animals tie? Write enough so that your thinking is clear.
seconds to go over and comes back at 40 feet/second. What should Turtle's speed be so that the animals tie? Write enough so that your thinking is clear.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
A) Someone buys a few candy bars at 55¢ each and several others on sale at 35¢ each. Is the average price for the candy bars 45¢? Explain.
B) A store sells two sizes of soft drinks: a large for $1.10 and a small for $0.90. Friday, the store sold 236 soft drinks. The manager reasons, "The $1.10 and $0.90 give an average of $1. So, we must have taken in $236 from soft drinks on Friday." Is the manager correct/incorrect? Explain in some detail.
B) A store sells two sizes of soft drinks: a large for $1.10 and a small for $0.90. Friday, the store sold 236 soft drinks. The manager reasons, "The $1.10 and $0.90 give an average of $1. So, we must have taken in $236 from soft drinks on Friday." Is the manager correct/incorrect? Explain in some detail.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
Tell whether each is correct and explain why or why not.
A) Fund-raiser: "We got two donations of $5000 and two of $1000 each! That's an average of $3000 per donation!"
B) Quality-control trainee: "One shipment had 1% of the items defective, and another shipment had 5% defective. That's an average of 3% defective."
A) Fund-raiser: "We got two donations of $5000 and two of $1000 each! That's an average of $3000 per donation!"
B) Quality-control trainee: "One shipment had 1% of the items defective, and another shipment had 5% defective. That's an average of 3% defective."

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
There is a (common) error, or some confusion, in each of the following situations. Find the error/confusion, and explain why some thinking was off, even though the person thought the thinking was all right.
A) Before summer school, a student had completed 96 units, with a GPA of 2.9. The student takes two three-unit courses in summer school and gets an A and a B for a 3.5 GPA. The student is pleased on calculating and finding the new GPA to be 3.2.
B) A teenager says she never has anything nice to wear. Her parents tell her she can buy four new blouses for her birthday but to keep the average price at $25 (or less). The girl finds some $40 blouses she really likes and calculates from = 25 that x = 10. So a $40 blouse and a $10 blouse would give an average of $25. She is happy to find an acceptable $10 blouse on a sale table. She buys that one and three of the $40 blouses in different colors.
C) A person bought a used car and wants to check its gas mileage. For the first few fill-ups, she covered 823 miles and got 24.4 miles/gallon. The next fill-up, after 240 more miles, took 6 gallons, so she got 40 miles/gallon. She calculates = 32.2 miles/gallon.
A) Before summer school, a student had completed 96 units, with a GPA of 2.9. The student takes two three-unit courses in summer school and gets an A and a B for a 3.5 GPA. The student is pleased on calculating and finding the new GPA to be 3.2.
B) A teenager says she never has anything nice to wear. Her parents tell her she can buy four new blouses for her birthday but to keep the average price at $25 (or less). The girl finds some $40 blouses she really likes and calculates from = 25 that x = 10. So a $40 blouse and a $10 blouse would give an average of $25. She is happy to find an acceptable $10 blouse on a sale table. She buys that one and three of the $40 blouses in different colors.
C) A person bought a used car and wants to check its gas mileage. For the first few fill-ups, she covered 823 miles and got 24.4 miles/gallon. The next fill-up, after 240 more miles, took 6 gallons, so she got 40 miles/gallon. She calculates = 32.2 miles/gallon.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
Abe got 94 out of 100 on one test but only 26 out of 50 on a second. He figures he has 94 + 26, or 120, out of 150 and finds that to be 80%. Hence, he cannot understand why his teacher's grade book shows a different result: 94% and 52%, which give an average of = 73%. What accounts for the difference?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
Give an example of a function that does NOT involve numbers exclusively.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
A) Find a function rule 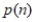 that gives the perimeter (distance around the outside) of the n-module in the pattern below. (Use the shortest segment as the measuring unit.) Show your work. Simplify by collecting any like terms.
that gives the perimeter (distance around the outside) of the n-module in the pattern below. (Use the shortest segment as the measuring unit.) Show your work. Simplify by collecting any like terms.
B) Justify that your rule in part A will always work.
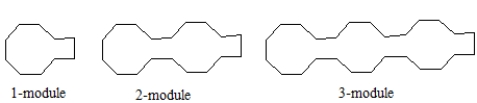
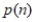 that gives the perimeter (distance around the outside) of the n-module in the pattern below. (Use the shortest segment as the measuring unit.) Show your work. Simplify by collecting any like terms.
that gives the perimeter (distance around the outside) of the n-module in the pattern below. (Use the shortest segment as the measuring unit.) Show your work. Simplify by collecting any like terms. B) Justify that your rule in part A will always work.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose that 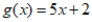
and h(x) is defined by machine X below. Give the output if 3 is the input to each of the following combinations.
A) first h(x) then g(x)
B) first g(x) then h(x)
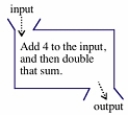
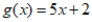
and h(x) is defined by machine X below. Give the output if 3 is the input to each of the following combinations.
A) first h(x) then g(x)
B) first g(x) then h(x)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
What does it mean to say, "the combination of functions is not commutative"?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
Consider these three function rules: ![<strong>Consider these three function rules: Give the final output if 2 is the input to each of the following combinations.</strong> A) The combination is [first f(x) then g(input)] and then h(output from that combination). In other words, the output of f is the input for g, and the input of that combination is the input for h. B) The output from f(x) is the input to the combination of g and h [first g(input) then h(input)]. In other words, combine g and h and use this new function to combine with f. C) What do your results from parts A and B suggest about associativity of combinations of functions? (Note to the instructor: Use this item cautiously, unless you have treated associativity.)](https://storage.examlex.com/TBMC1056/11eddf53_a361_3693_b94d_5f05bbe5e9df_TBMC1056_00.jpg)
Give the final output if 2 is the input to each of the following combinations.
A) The combination is [first f(x) then g(input)] and then h(output from that combination). In other words, the output of f is the input for g, and the input of that combination is the input for h.
B) The output from f(x) is the input to the combination of g and h [first g(input) then h(input)]. In other words, combine g and h and use this new function to combine with f.
C) What do your results from parts A and B suggest about associativity of combinations of functions? (Note to the instructor: Use this item cautiously, unless you have treated associativity.)
![<strong>Consider these three function rules: Give the final output if 2 is the input to each of the following combinations.</strong> A) The combination is [first f(x) then g(input)] and then h(output from that combination). In other words, the output of f is the input for g, and the input of that combination is the input for h. B) The output from f(x) is the input to the combination of g and h [first g(input) then h(input)]. In other words, combine g and h and use this new function to combine with f. C) What do your results from parts A and B suggest about associativity of combinations of functions? (Note to the instructor: Use this item cautiously, unless you have treated associativity.)](https://storage.examlex.com/TBMC1056/11eddf53_a361_3693_b94d_5f05bbe5e9df_TBMC1056_00.jpg)
Give the final output if 2 is the input to each of the following combinations.
A) The combination is [first f(x) then g(input)] and then h(output from that combination). In other words, the output of f is the input for g, and the input of that combination is the input for h.
B) The output from f(x) is the input to the combination of g and h [first g(input) then h(input)]. In other words, combine g and h and use this new function to combine with f.
C) What do your results from parts A and B suggest about associativity of combinations of functions? (Note to the instructor: Use this item cautiously, unless you have treated associativity.)

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
Find a function rule for the following data.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
Find a function rule for the following data.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
Find a function rule for the following data.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Find a function rule for the following data.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
What is the HIGHEST power of x that could be involved in the polynomial function rule for these data? Tell how you know.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck


