Deck 10: Integers and Other Number Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/24
Play
Full screen (f)
Deck 10: Integers and Other Number Systems
1
Complete the following. For each subtraction problem, first rewrite it as an addition problem.
A) -7 + -8 =
B) 3 + -5 =
C) 16 + -14 =
D) -21 + -2 =
E) 17 - -3 =
F) -2 - -5 =
G) -13 - 9 =
H) 14 - -16 =
I)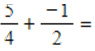
J)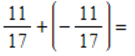
K) -2.6 - 4.5 =
L) -3.17 - 2.4 =
A) -7 + -8 =
B) 3 + -5 =
C) 16 + -14 =
D) -21 + -2 =
E) 17 - -3 =
F) -2 - -5 =
G) -13 - 9 =
H) 14 - -16 =
I)
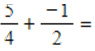
J)
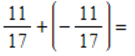
K) -2.6 - 4.5 =
L) -3.17 - 2.4 =
A) -15
B) -2
C) 2
D) -23
E) 17 - -3 = 17 + 3 = 20
F) -2 - -5 = -2 + 5 = 3
G) -13 - 9 = -13 + -9 = -22
H) 14 - -16 = 14 + 16 = 30
I)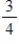
J) 0
K) -2.6 + -4.5 = -7.1
L) -3.17 + -2.4 = -5.57
B) -2
C) 2
D) -23
E) 17 - -3 = 17 + 3 = 20
F) -2 - -5 = -2 + 5 = 3
G) -13 - 9 = -13 + -9 = -22
H) 14 - -16 = 14 + 16 = 30
I)
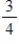
J) 0
K) -2.6 + -4.5 = -7.1
L) -3.17 + -2.4 = -5.57
2
Reorder these numbers from smallest to largest: 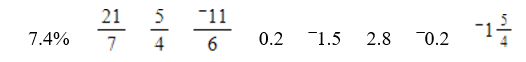
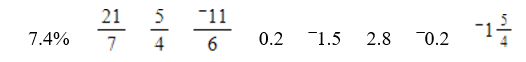
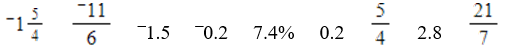
3
Complete this "fact family" table: 


4
Is the statement a + b = |a| - |b| always true, sometimes true, or never true? Explain your answer.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
5
Use diagrams to explain how one could use white (positive) and dark (negative) chips to model the following:
A) 4 + (-6)
B) 5 - (-2)
A) 4 + (-6)
B) 5 - (-2)

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
6
Which property does each of the following involve?
A) (-2 + 3) + -5 = (3 + -2) + -5
B) (-2 + 3) + -5 = -5 + (3 + -2)
C) (-2 + 3) + -5 = -2 +(3 + -5)
A) (-2 + 3) + -5 = (3 + -2) + -5
B) (-2 + 3) + -5 = -5 + (3 + -2)
C) (-2 + 3) + -5 = -2 +(3 + -5)

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
7
Does zero have a multiplicative inverse? Explain.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
8
Complete the following.
A) -7 × -8 =
B) 3 × -5 =
C) 16 × -2 =
D) -21 × -2 =
E) 18 ÷ -3 =
F) -2 ÷ -5 =
G) -18 ÷ 9 =
H) 4 ÷ -16 =
I)
J)
K) -8.6 ÷ 4.3 =
L) -1.2 ÷ -2.4 =
A) -7 × -8 =
B) 3 × -5 =
C) 16 × -2 =
D) -21 × -2 =
E) 18 ÷ -3 =
F) -2 ÷ -5 =
G) -18 ÷ 9 =
H) 4 ÷ -16 =
I)
J)
K) -8.6 ÷ 4.3 =
L) -1.2 ÷ -2.4 =

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
9
A) Continue the following pattern of multiplication of integers with six more products in the pattern.
4 × 4 = 16
3 × -4 = -12
2 × -4 = -8 . . .
B) The multipliers decrease by _____ each time. The multiplicand is always -4. The product _____ by _____ each time. For this pattern to continue working, the product of two negative integers must be _____.


4 × 4 = 16
3 × -4 = -12
2 × -4 = -8 . . .
B) The multipliers decrease by _____ each time. The multiplicand is always -4. The product _____ by _____ each time. For this pattern to continue working, the product of two negative integers must be _____.



Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
10
Give the exact answer to each of the following, taking advantage of properties. Then tell which property or properties enabled you to answer them so easily.
A) If 213 × 142 = 41,401, then 142 × 213 = _____.
B)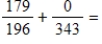 _____
_____
C) 84.96 × 100% = _____
D) (548 + -967) + -548 = _____
A) If 213 × 142 = 41,401, then 142 × 213 = _____.
B)
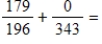 _____
_____ C) 84.96 × 100% = _____
D) (548 + -967) + -548 = _____

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
11
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Associative property of multiplication
_____ A) -3 × (2 + 5) = -3 × (5 + 2)
_____ B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
_____ C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
_____ D) 5 + (8 + 0) = 5 + 8
_____ E) -4 × 1 = -4
_____ F) 6 + (4 + -4) = 6 + 0
_____ G)
_____H)
_____ I) 3 + (2 + -5) = (3 + 2) + -5
A:Commutative property of multiplication
B : Distributive property
C : Associative property of addition
D : Identity property of addition
E : Identity property of multiplication
F : Inverse property of addition
G : Inverse property of multiplication
H : Associative property of multiplication
I : Associative property of addition
-Associative property of multiplication
_____ A) -3 × (2 + 5) = -3 × (5 + 2)
_____ B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
_____ C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
_____ D) 5 + (8 + 0) = 5 + 8
_____ E) -4 × 1 = -4
_____ F) 6 + (4 + -4) = 6 + 0
_____ G)
_____H)
_____ I) 3 + (2 + -5) = (3 + 2) + -5
A:Commutative property of multiplication
B : Distributive property
C : Associative property of addition
D : Identity property of addition
E : Identity property of multiplication
F : Inverse property of addition
G : Inverse property of multiplication
H : Associative property of multiplication
I : Associative property of addition

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
12
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Additive identity property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Additive identity property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
13
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Multiplicative inverse property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Multiplicative inverse property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
14
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Additive inverse property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Additive inverse property
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
15
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Commutative property of addition
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Commutative property of addition
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
16
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Associative property of addition
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Associative property of addition
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
17
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Distributive property of × over +
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Distributive property of × over +
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
18
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Multiplicative identity property
?
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Multiplicative identity property
?
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
19
Match the operations and the names of the properties by placing the correct number to the left of the letters A-I. (Not all properties on the right will necessarily be used; some may be used more than once.)
-Commutative property of multiplication
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5
-Commutative property of multiplication
A) -3 × (2 + 5) = -3 × (5 + 2)
B) 3 × (2 + 5) = (3 × 2) + (3 × 5)
C) 4 + (-3 + -1) + 2 = (4 + -3) + (-1 + 2)
D) 5 + (8 + 0) = 5 + 9
E) -4 × 1 = -4
F) 6 + (4 + -4) = 6 + 0
G)
H)
I) 3 + (2 + -5) = (3 + 2) + -5

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
20
Consider clock arithmetic using a clock with four numbers: 0, 1, 2, and 3.
A) Complete these tables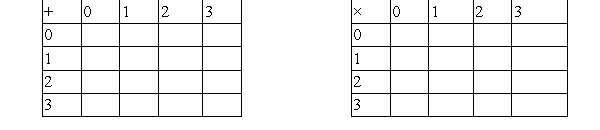 B) Do you think the set of numbers-0, 1, 2, and 3-is closed under addition? If not, provide an example that shows it is not.
B) Do you think the set of numbers-0, 1, 2, and 3-is closed under addition? If not, provide an example that shows it is not.
C) Do you think the set of numbers-0, 1, 2, and 3-is closed under multiplication? If not, provide an example that shows it is not.
D) Is there an additive identity? If so, what is it?
E) Is there a multiplicative identity? If so, what is it?
F) Does 3 have an additive inverse? If so, what is it?
G) Does 2 have a multiplicative inverse? If so, what is it?
H) Do you think addition is commutative? If so, how do we know that as we look at the table?
I) Do you think multiplication is commutative? If so, how do we know that as we look at the table?
J) Do you think addition is associative? If so, provide at least three examples.
K) Do you think multiplication is associative? If so, provide at least three examples.
L) Do you think multiplication is distributive over addition? If so, provide at least three examples.
A) Complete these tables
 B) Do you think the set of numbers-0, 1, 2, and 3-is closed under addition? If not, provide an example that shows it is not.
B) Do you think the set of numbers-0, 1, 2, and 3-is closed under addition? If not, provide an example that shows it is not.C) Do you think the set of numbers-0, 1, 2, and 3-is closed under multiplication? If not, provide an example that shows it is not.
D) Is there an additive identity? If so, what is it?
E) Is there a multiplicative identity? If so, what is it?
F) Does 3 have an additive inverse? If so, what is it?
G) Does 2 have a multiplicative inverse? If so, what is it?
H) Do you think addition is commutative? If so, how do we know that as we look at the table?
I) Do you think multiplication is commutative? If so, how do we know that as we look at the table?
J) Do you think addition is associative? If so, provide at least three examples.
K) Do you think multiplication is associative? If so, provide at least three examples.
L) Do you think multiplication is distributive over addition? If so, provide at least three examples.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
21
Reorder these numbers from largest to smallest without using decimals:

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
22
Place the following on a number line:
- -
- -

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
23
Illustrate how to use motion on the number line to find the difference.
A) -5 - _____ = -10
B) 3 - 8 = _____
A) -5 - _____ = -10
B) 3 - 8 = _____

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
24
Illustrate how to use the missing-addend view of subtraction on the number line to find the difference.
A) 3 - -4 = _____
B) -2 - -5 = _____
A) 3 - -4 = _____
B) -2 - -5 = _____

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck


