Deck 4: Some Conventional Ways of Computing
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/17
Play
Full screen (f)
Deck 4: Some Conventional Ways of Computing
1
Show 3335 ÷ 23 with a scaffolding algorithm and then by the standard algorithm. Show how each number in the standard algorithm is associated with each number in the scaffolding algorithm.

In the second algorithm, the 23 actually is 2300, yielding 100 in the quotient. The 103 is actually 1030, from which 920 (i.e., 23 × 40, which is 460 twice, making the first division easier) is subtracted, leaving 115 in both algorithms. In the first algorithm, 115 ÷ 23 is done in two steps, and in one step in the second algorithm, both times yielding 5. The first scaffolding algorithm could be done in multiple ways yielding the same result.
2
Use the scaffolding method to compute 5883 ÷ 17.
Something along the lines of the following, which unnecessarily gives the best guesses for each place value (one of the talking points for the scaffolding algorithm): 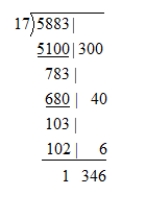
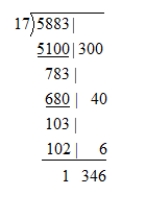
3
Show, using 324 ÷ 28, how to work from the scaffolding algorithm to the standard algorithm.
Similar to question 1. Students' work should show an awareness of the scaffolding algorithm format to an abbreviated form to the usual US form.
4
Do 32 × 467 using the method of writing all partial products.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
5
Use a nonstandard algorithm to find 240five + 314five, but showing all partial sums.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
6
Name two positive and two negative aspects of learning nonstandard algorithms.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
7
Make a drawing of base-ten materials that shows the initial setup for 3 × 130.2. Make clear what = 1. Do not take time to draw all the later steps of the calculation with the base ten materials.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
8
Draw how one would act out 200 - 62 (take-away view) to support the usual right-left algorithm, with base-ten materials. (Make clear what represents 1.) Make a separate drawing for each step (add steps if you need them).

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
9
Draw how one would act out 200 - 62 (comparison view) to support the usual right-left algorithm, with base-ten materials. (Make clear what represents 1.) Make a separate drawing for each step (add steps if you need them).

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
10
You decide to introduce your fourth-graders to the long-division algorithm with one-digit divisors, using base-ten materials and 96 ÷ 3. You also want to use a story problem that they would find interesting as the basis for their work.
A) From the practical standpoint of acting out the calculation, which way of thinking about division-repeated subtraction or sharing equally-should you use in your story problem for 96 ÷ 3?
B) Write such a story problem (involving 96 ÷ 3).
C) Show how you would act out your story problem, with drawings of the base-ten materials.
D) Write a second story problem for 96 ÷ 3, involving a different way of thinking about division from the way of thinking in your story problem in part
E) Answer parts A-D if you were to use 960 ÷ 320 instead of 96 ÷ 3.
A) From the practical standpoint of acting out the calculation, which way of thinking about division-repeated subtraction or sharing equally-should you use in your story problem for 96 ÷ 3?
B) Write such a story problem (involving 96 ÷ 3).
C) Show how you would act out your story problem, with drawings of the base-ten materials.
D) Write a second story problem for 96 ÷ 3, involving a different way of thinking about division from the way of thinking in your story problem in part
E) Answer parts A-D if you were to use 960 ÷ 320 instead of 96 ÷ 3.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
11
A student places multi-base blocks on the table as follows: 
Write which calculation the student might be doing.

Write which calculation the student might be doing.


Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
12
What would the NEXT line be in a Russian peasant calculation of 23 × 621?
You do not have to do the complete algorithm.
23 × 621
A) 11 × 1242
B) 46 × 310
C) 23 × 21
D) 11 × 1242 or possibly 46 × 310
E) 46 × 310 or possibly 23 × 21
You do not have to do the complete algorithm.
23 × 621
A) 11 × 1242
B) 46 × 310
C) 23 × 21
D) 11 × 1242 or possibly 46 × 310
E) 46 × 310 or possibly 23 × 21

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
13
The Russian peasant method for multiplying uses two basic processes: doubling and _____.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
14
Below is a worked-out calculation of 313 × 42, using the lattice method for multiplication. Explain why the method does give the correct number in the tens place (the circled 4). (Note: Some current textbooks use this algorithm to teach multiplication of whole numbers.) 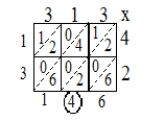


Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
15
Write a word problem that would require solving 540 ÷ 4.

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
16
Consider this arithmetic problem: 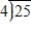
A) Write a story problem where the answer would be 6.
B) Write a story problem where the answer would be 7.
C) Write a story problem where the answer would be 1.
D) Write a story problem where the answer would be 6
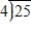
A) Write a story problem where the answer would be 6.
B) Write a story problem where the answer would be 7.
C) Write a story problem where the answer would be 1.
D) Write a story problem where the answer would be 6

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
17
A student's work on a base-ten subtraction problem is shown below. How much does the little 1 above the 5 represent? 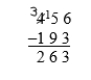
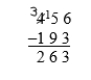

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck


