Deck 4: The Sampling Distribution and Estimation Procedures
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 4: The Sampling Distribution and Estimation Procedures
1
In 2013, 50 incidents of DUI-Liquor were reported (source: Seattle Police Department Police Report Incident database). Assume you have a list of the individuals behind the numbers, meaning the individual DUI offenders. From this list, you create a random sample of 15 DUI offenders using a random numbers table or a statistics program.
a. What are the three essential requirements for a simple random sample? Indicate and explain why these are fulfilled in the example above (DUI).
i. _______________
ii. _______________
iii. _______________
b. What is the probability of an individual DUI offender to be selected into the sample?
a. What are the three essential requirements for a simple random sample? Indicate and explain why these are fulfilled in the example above (DUI).
i. _______________
ii. _______________
iii. _______________
b. What is the probability of an individual DUI offender to be selected into the sample?
a. The requirements for a simple random sample are:
i.A defined population (all DUI offenders in the year 2013 in Seattle).
ii.An exhaustive list of all members of the population (we assume to have this list).
iii.A selection process that assures that every case or group of cases in the population has an equal chance of being selected.
b. 15/50 = 0.3
The probability of being selected is 0.3, or 30%.
i.A defined population (all DUI offenders in the year 2013 in Seattle).
ii.An exhaustive list of all members of the population (we assume to have this list).
iii.A selection process that assures that every case or group of cases in the population has an equal chance of being selected.
b. 15/50 = 0.3
The probability of being selected is 0.3, or 30%.
2
Find out how many unique samples of 15 DUI offenders can be drawn from the population of all (50) DUI offenders in Seattle in the year 2013.
To calculate the number of possible unique samples, we use formula 5-1:
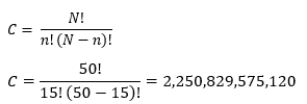
The total number of unique samples of 15 that can be drawn from a population of 50 is 2,250,829,575,120. 2.
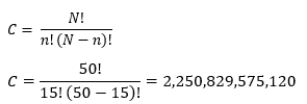
The total number of unique samples of 15 that can be drawn from a population of 50 is 2,250,829,575,120. 2.
3
Assume that you are especially interested in DUI offenders (2013) with extensive prior traffic violations (5+) other than parking infractions. Assume that records indicate that 6 of the 50 DUI offenders have 5+ prior traffic violations. These 6 individuals represent your new population. The numbers of traffic offenses (prior to the DUI in 2013) for each individual are 5, 11, 7, 9, 6, and 10. Assume that we want to draw a sample of 3 individuals.
a. How many unique samples can be drawn with n = 6 and n = 3?
b. What is the mean of each individual sample? What is the standard deviation of each individual sample?
c. Find the mean of means and the standard error of the sampling distribution.
d. What are the mean and the standard deviation of the entire population?
e. Calculate the standard error.
a. How many unique samples can be drawn with n = 6 and n = 3?
b. What is the mean of each individual sample? What is the standard deviation of each individual sample?
c. Find the mean of means and the standard error of the sampling distribution.
d. What are the mean and the standard deviation of the entire population?
e. Calculate the standard error.
a. Use formula 5-1:
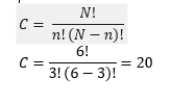
b.
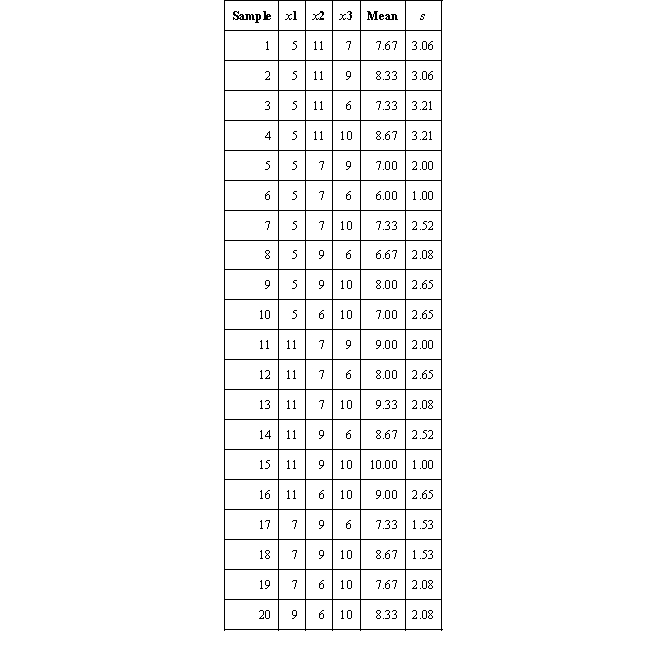
c. Mean of means = 8.00; standard error of sampling distribution = 2.28.
d. Population mean = 8.00; standard deviation (population) = 2.37.
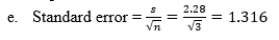
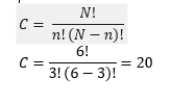
b.

c. Mean of means = 8.00; standard error of sampling distribution = 2.28.
d. Population mean = 8.00; standard deviation (population) = 2.37.
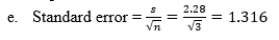
4
What is the difference between a point estimate and an interval estimate? Apply your knowledge to the following and indicate whether it is a point or an interval estimate.
a. The average grade point average of all students in the Criminal Justice Program is 3.3.
b. The average student within the Criminal Justice Program takes on a credit load between 9 and 12 credits.
c. Between 1990 and 2012 an average of 12% of students dropped out the Criminal Justice Program.
a. The average grade point average of all students in the Criminal Justice Program is 3.3.
b. The average student within the Criminal Justice Program takes on a credit load between 9 and 12 credits.
c. Between 1990 and 2012 an average of 12% of students dropped out the Criminal Justice Program.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
Recall our problem from chapter 4 (No. 7) where we were interested in the number of citizen complaints an individual officer received in 2013. We know that the sample mean "citizen complaint" is 8.4 and that n = 15 and the standard deviation is 6.75.
a. Calculate the standard error.
b. If an infinite number of sample means would be drawn, what percentage of police officers/citizen complaints will fall between ±1 standard deviation of the mean?
c. What range of citizen complaints would that be (with a standard error of 1.7)?
d. What is the range of citizen complaints/officer within 3 standard deviations from the mean (±)?
e. What is the technical term for these ranges?
a. Calculate the standard error.
b. If an infinite number of sample means would be drawn, what percentage of police officers/citizen complaints will fall between ±1 standard deviation of the mean?
c. What range of citizen complaints would that be (with a standard error of 1.7)?
d. What is the range of citizen complaints/officer within 3 standard deviations from the mean (±)?
e. What is the technical term for these ranges?

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
Answer the following questions:
a. What does the α level indicate?
b. How is α selected?
c. How many times of 100 is a researcher willing to be wrong (true population parameter not within the confidence range) if he or she selects an α level of
i. 0.05?
ii. 0.01?
iii. 0.001?
a. What does the α level indicate?
b. How is α selected?
c. How many times of 100 is a researcher willing to be wrong (true population parameter not within the confidence range) if he or she selects an α level of
i. 0.05?
ii. 0.01?
iii. 0.001?

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
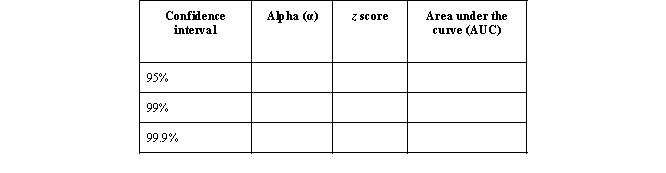
The most commonly used confidence intervals are 95%, 99%, and 99.90%. Thus, it is helpful to remember the corresponding α levels (which is easy), z values, and corresponding areas under the curve. Fill in the corresponding values in the table below.


Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
Your school randomly selects a sample of 150 students (of 2,567) and asks them about their experiences with crime. The results of victimization within the past 12 months show that the average student experienced 5.8 victimizations within the past 12 months (s = 3.1). Find the 95% confidence interval and interpret your results.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
The same students (n = 150) were also asked how often in their life they have stolen something of a value of $5+. The average number was found to be 7.2 (s = 4.3). Find the 99% confidence interval and interpret your results.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
Inspired by the survey conducted by your school, you plan your own study examining victimization rates of students enrolled in colleges or universities in your city and you are aiming for a confidence interval of 95%. Also assume that you want to be wrong by only one victimization on either side of the population mean. You are wondering what sample size you should select. You know the mean ( 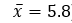 ) and standard deviation (s = 3.1) of the study conducted by your school (you are treating it as a pilot study). Calculate the adequate sample size.
) and standard deviation (s = 3.1) of the study conducted by your school (you are treating it as a pilot study). Calculate the adequate sample size.
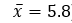 ) and standard deviation (s = 3.1) of the study conducted by your school (you are treating it as a pilot study). Calculate the adequate sample size.
) and standard deviation (s = 3.1) of the study conducted by your school (you are treating it as a pilot study). Calculate the adequate sample size.
Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck


