Deck 12: Bargaining

Question 1

Nash bargaining refers to:

A) A noncooperative, finitely-repeated game in which the players bid against each other to acquire the right to purchase or sell something of value.
B) A noncooperative, one-time game in which the players compete over the distribution of a divisible amount or object of value.
C) A written or oral agreement in which two more individuals promises to reform, or refrain from performing a some specified act in exchange for some valuable
benefit or consideration.
D) An infinitely-repeated game in which both players have an incentive to collude.
E) None of the above are correct.

Answer 1

A noncooperative, one-time game in which the players compete over the distribution of a divisible amount or object of value.

Question 2

Nash bargaining is an example of a:

A) Coordination game.
B) Bertrand price-setting game.
C) Cooperative, repeated, static game.
D) Prisoner's dilemma.
E) All of the above.

Answer 2

Coordination game.

Question 3

A buyer's reservation price in bargaining is:

A) The minimum price that a buyer is willing to pay.
B) The maximum price that a seller is willing to pay.
C) The minimum price that a seller is willing to accept.
D) The maximum price that a buyer is willing to accept.

Answer 3

The maximum price that a seller is willing to pay.

Question 4

A seller's reservation price in bargaining is:

A) The minimum price that a buyer is willing to pay.
B) The maximum price that a seller is willing to pay.
C) The minimum price that a seller is willing to accept.
D) The maximum price that a buyer is willing to accept.

Question 5

Suppose that management and labor are bargaining over how much of a surplus to give to workers. The $100 can be divided into $25 increments. The sides simultaneously write the amount that they want on a piece of paper. If the sum of the amounts does not exceed $100 then the both sides get the amount that they asked for. If the sum of the amounts exceeds $100 then the bargaining ends in a stalemate. Assume that failure to come to an agreement costs both union and management $1. How many Nash equilibria does this game have?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 6

The bargaining situation described in question 12.1 is an example of a coordination game. The most likely outcome is the strategy profile:

A) {!1, !1}
B) {0, 0}
C) {50, 50}
D) {100, 0}
E) {0, 100}

Question 7

The ability of a bargaining player to dictate the final terms of a negotiated agreement is called a:

A) First-mover's advantage.
B) Strictly dominant strategy.
C) Last-mover advantage.
D) Bertrand paradox.
E) None of the above.

Question 8

Two individuals with diverse interests are bargaining over the distribution of $500 in which payoffs must be in increments of $10. Each player submits a one time bid. If the sum of the bids is less than or equal to $500, each player gets the amount of their bid and the game ends. If the sum of the bids exceed $500, the bargaining ends and the players go home empty handed. This bargaining game:

A) Has a unique Nash equilibrium.
B) Does not have a Nash equilibrium.
C) Has multiple Nash equilibria.
D) All of the above are possible.
E) There is not enough information to answer this question.

Question 9

Two individuals with diverse interests are bargaining over the distribution of $500 in which payoffs must be in increments of $10. Each player submits a one time bid. If the sum of the bids is less than or equal to $500, each player gets the amount of their bid and the game ends. If the sum of the bids exceed $500, the bargaining ends and the players go home empty handed. The most likely strategy profile for this game is:
I. {$0, $0}
II. {$10, $10}
II. {$500, $0}
III. {$0, $500}
IV {$250, $250)
Which of the following is correct?

A) I only.
B) II only.
C) III only.
D) IV only.
E) All of the above are equally likely.

Question 10

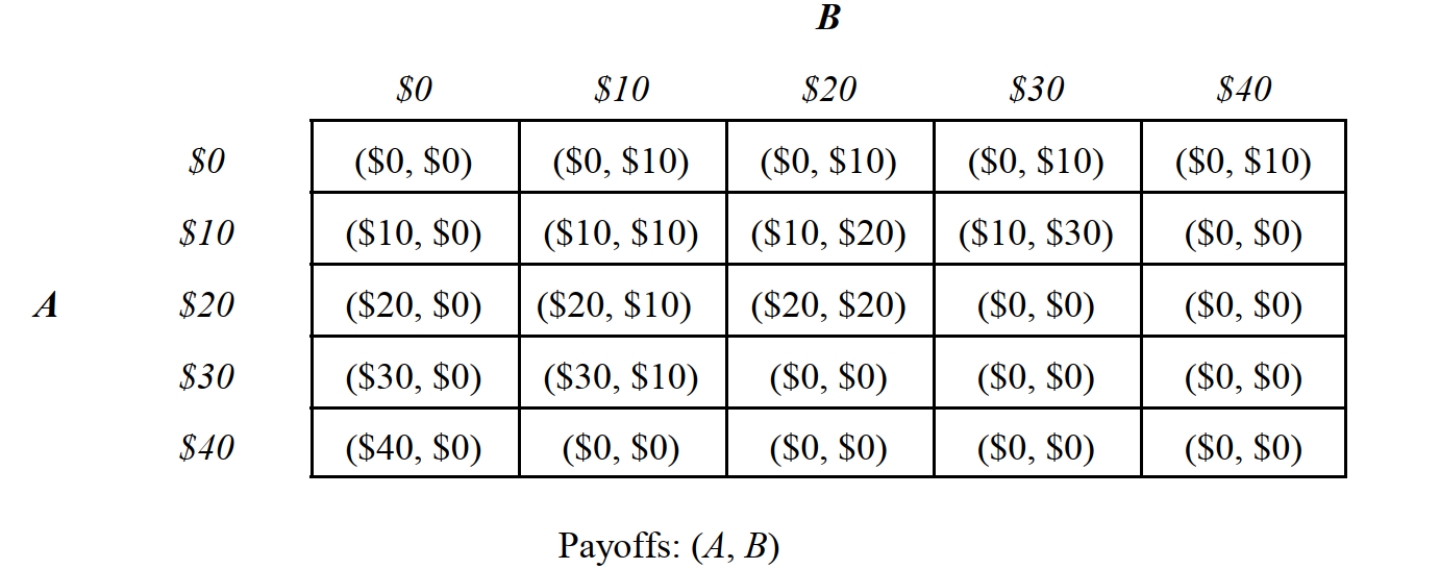
-Consider the one-time Nash bargaining game depicted in Figure 12.1 in which individuals A and B individuals are bargaining over the distribution of $40. Bids must be in increments of $10. In this game, the sum of the players' bids cannot exceed $40. If the sum of the bids are less than $40, each bidder receives his or her bid, and the rest goes to charity. If the sum of the bids exceeds $40, the bidders receive nothing, and $40 is given to charity. How many possible Nash equilibria are there for this game?

A) 1
B) 2
C) 3
D) 4
E) 5

Question 11

-Consider the one-time Nash bargaining game depicted in Figure 12.1 in which A and B individuals are bargaining over the distribution of $40. Bids must be in increments of $10. In this game, the sum of the players' bids cannot exceed $40. If the sum of the bids are less than $40, each bidder receives his or her bid, and the rest goes to charity. If the sum of the bids exceeds $40, the bidders receive nothing, and $40 is given to charity. The most likely Nash equilibrium strategy profile for this game is:

A) {$0, $0}.
B) {$10, $10}.
C) {$20, $20}.
D) {$40, $0}.
E) {$0, $40}.

Question 12

-Consider the one-time Nash bargaining game depicted in Figure 12.1 in which A and B individuals are bargaining over the distribution of $40. Bids must be in increments of $10. In this game, the sum of the players' bids cannot exceed $40. If the sum of the bids are less than $40, each bidder receives his or her bid, and the rest goes to charity. If the sum of the bids exceeds $40, the bidders receive nothing, and $40 is given to charity. The most likely explanation for the outcome of this bargaining game is:

A) Backward induction.
B) Minimax theorem.
C) Cournot model.
D) Maximin decision rule.
E) Bertrand paradox.

Question 13

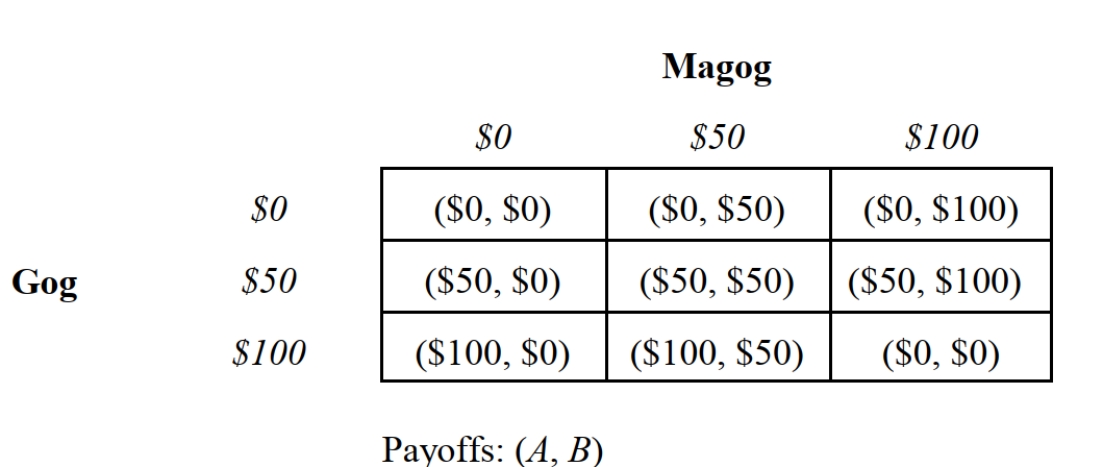
-Consider the one-time Nash bargaining game depicted in Figure 12.2 in which Gog and Magog are bargaining over the distribution of $100. Bids must be in increments of $50. In this game, the sum of the players' bids cannot exceed $100. If the sum of the bids are less than $100, each bidder receives his bid, and the rest is forfeited to the Exchequer. If the sum of the bids exceeds $100, the bidders receive nothing, and $100 is forfeited to the Exchequer. How many possible Nash equilibria are there for this game?

A) 0
B) 1
C) 2
D) 3
E) 4

Question 14

-Symmetric impatience refers to:

A) The equal reduction in patience by two players that fail to come to a bargaining agreement.
B) The equal reduction in payoffs by two players that fail to come to a bargaining agreement.
C) The equal reduction in each player's share of the bargaining surplus by failing to come to an agreement.
D) The equal reduction in each player's patience with a rival's refusal to bargain in good faith.
E) Answers b and c are correct.

Question 15

-Consider the one-time Nash bargaining game depicted in Figure 12.2 in which Gog andMagog are bargaining over the distribution of $100. Bids must be in increments of $50. In this game, the sum of the players' bids cannot exceed $100. If the sum of the bids are less than $100, each bidder receives his bid, and the rest is forfeited to the Exchequer. If the sum of the bids exceeds $100, the bidders receive nothing, and $100 is forfeited to the Exchequer. The most likely Nash equilibrium strategy profile for this game is:

A) {$0, $0}.
B) {$50, $50}.
C) {$0, $100}.
D) {$100, $0}.
E) Answers c and d are equally likely.

Question 16

-Consider the one-time Nash bargaining game depicted in Figure 12.2 in which Gog andMagog are bargaining over the distribution of $100. Bids must be in increments of $50. In this game, the sum of the players' bids cannot exceed $100. If the sum of the bids are less than $100, each bidder receives his bid, and the rest is forfeited to the Exchequer. If the sum of the bids exceeds $100, the bidders receive nothing, and $100 is forfeited to the Exchequer. The most likely explanation for the outcome of this bargaining game is the:

A) Savage theorem.
B) Bertrand paradox.
C) Cournot model.
D) Minimax theorem.
E) Stackelberg theorem.

Question 17

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose Andrew makes the first offer and there is an even number offers and counteroffers. If Andrew and Adam are equally patient, Adam will sell his car for:

A) $1,000.
B) $1,500.
C) $2,000.
D) Somewhere between $1,000 and $2,000, but the exact amount cannot be determined without knowing Andrew's and Adam's opportunity cost per negotiating round.
E) Cannot be determined without first knowing the number of negotiating rounds.

Question 18

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose Andrew makes the first offer and there is an odd number offers and counteroffers. If Andrew and Adam are equally patient, Adam will sell his car for:

A) $1,000.
B) $1,500.
C) $2,000.
D) Somewhere between $1,000 and $2,000, but the exact amount cannot be determined without knowing Andrew's and Adam's opportunity cost per negotiating round.
E) Cannot be determined without first knowing the number of negotiating rounds.

Question 19

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose Andrew makes the first offer and there is an even number offers and counteroffers. If Andrew and Adam are equally patient:

A) Andrew enjoys a negotiating advantage because he moves first.
B) Adam enjoys a negotiating advantage because he is the seller.
C) Andrew enjoys a negotiating advantage because he makes the last counteroffer.
D) Adam enjoys a negotiating advantage because he makes the last counteroffer.
E) Andrew's advantage increases with the number of negotiating rounds.

Question 20

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose Andrew makes the first offer and there is an odd number offers and counteroffers. If Andrew and Adam are equally patient:

A) Andrew enjoys a negotiating advantage because he moves first.
B) Adam enjoys a negotiating advantage because he is the seller.
C) Andrew enjoys a negotiating advantage because he makes the last counteroffer.
D) Adam enjoys a negotiating advantage because he makes the last counteroffer.
E) Andrew's advantage increases with the number of negotiating rounds.

Question 21

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from bargaining by 10 percent. If there is no limit to the number of negotiating rounds, how much should Andrew offer for Adam's car?

A) $1,000.
B) An amount that is somewhat greater than $1,500.
C) An amount that is somewhat less than $1,500.
D) $2,000.
E) None of the above since Andrew and Adam will be unable to negotiate a selling price.

Question 22

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent. If there is no limit to the number of negotiating rounds, how much should Adam accept for his car?

A) $1,000
B) An amount that is somewhat greater than $1,500
C) An amount that is somewhat less than $1,500
D) $2,000
E) None of the above since Andrew and Adam will be unable to negotiate a selling price.

Question 23

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent. If there is no limit to the number of negotiating rounds, what percentage of the bargaining surplus should Adam receive?

A) Around 51 percent.
B) Around 53 percent.
C) Around 57 percent.
D) Around 62 percent.
E) None of the above.

Question 24

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent. If there is no limit to the number of negotiating rounds, what percentage of the bargaining surplus should Andrew receive?

A) Around 49 percent.
B) Around 47 percent.
C) Around 43 percent.
D) Around 38 percent.
E) None of the above.

Question 25

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent and 5 percent, respectively. If there is no limit to the number of negotiating rounds, what price should Andrew offer Adam in the first round?

A) An amount around $1,110.
B) An amount around $1,330.
C) An amount around $1,530.
D) An amount around $1,690.
E) An amount around $1,770.

Question 26

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent and 5 percent, respectively. If there is no limit to the number of negotiating rounds, what percentage of the bargaining surplus will Andrew receive?

A) Around 28 percent.
B) Around 30 percent.
C) Around 31 percent.
D) Around 41 percent.
E) Around 49 percent.

Question 27

Andrew wants to purchase Adam's car. Andrew is prepared to pay a maximum of $2,000. Adam is not willing to accept anything lower than $1,000. Suppose that any failure to reach an agreement reduces Andrew's and Adam's gain from reaching an agreement by 10 percent and 5 percent, respectively. If there is no limit to the number of negotiating rounds, what percentage of the bargaining surplus will Adam receive?

A) Around 51 percent.
B) Around 59 percent.
C) Around 69 percent.
D) Around 70 percent.
E) Around 72 percent.

Question 28

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to$2,500. Polly will not sell the doll house for less than $2,000. Polly has discovered,however, that Molly has $2,500 to spend. Molly and Polly are prepared to bargain over the doll house until "hell freezes over." If Molly makes the first offer and there are an even number of offers and counteroffers, Polly will end up selling the doll house for:

A) $2,000.
B) $2,500.
C) $2,250.
D) Cannot be determined without knowing the precise number of negotiating rounds.
E) None of the above.

Question 29

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Polly has discovered, however, that Molly has $2,500 to spend. Molly and Polly are prepared to bargain over the doll house until "hell freezes over." If Molly makes the first offer and there are an odd number of offers and counteroffers, Polly will end up selling the doll house for:

A) $2,000.
B) $2,500.
C) $2,250.
D) Cannot be determined without knowing the precise number of negotiating rounds.
E) None of the above.

Question 30

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Molly and Polly are prepared to bargain over the doll house until "hell freezes over." Suppose Molly makes the first offer, there is an even number bargaining rounds.

A) Polly has a bargaining advantage because she makes the last counteroffer.
B) Andrew's advantage increases with the number of negotiating rounds.
C) Molly has a bargaining advantage because she moves first.
D) Polly has a bargaining advantage because she is the seller.
E) Molly has a bargaining advantage because she makes the last counteroffer.

Question 31

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Molly and Polly are prepared to bargain over the doll house until "hell freezes over." Suppose Molly makes the first offer, there is an odd number bargaining rounds.

A) Polly has a bargaining advantage because she makes the last counteroffer.
B) Andrew's advantage increases with the number of negotiating rounds.
C) Molly has a bargaining advantage because she moves first.
D) Polly has a bargaining advantage because she is the seller.
E) Molly has a bargaining advantage because she makes the last counteroffer.

Question 32

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Polly has discovered, however, that Molly has $2,500 to spend. Suppose that any failure to reach an agreement reduces Molly's and Polly's gain by 20 percent. If there is no limit to the number of bargaining rounds, how much should Molly offer for the antique doll house? :

A) $2,000.
B) An amount between $2,000 and $2,250.
C) An amount between$2,250 and $2,500.
D) $2,500.
E) None of the above since Andrew and Adam will be unable to negotiate a selling price.

Question 33

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Suppose that any failure to reach an agreement reduces Molly's and Polly's gain by 20 percent. If there is no limit to the number of bargaining rounds, how much should Polly accept for the antique doll house?

A) $2,000.
B) An amount somewhat less than $2,250.
C) An amount somewhat greater than $2,750.
D) $2,500.
E) None of the above since Andrew and Adam will be unable to negotiate a selling price.

Question 34

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to$2,500. Polly will not sell the doll house for less than $2,000. Suppose that any failure to reach an agreement reduces Molly's gain by 15 percent and will reduce Polly's gain by 25 percent. If there is no limit to the number of bargaining rounds, how much should Molly offer for the antique doll house?

A) An amount between $2,110 and $2,120.
B) An amount between $2,150 and $2,160.
C) An amount between $2,200 and $2,210.
D) An amount between $2,230 and $2,240.
E) None of the above.

Question 35

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Suppose that any failure to reach an agreement reduces Molly's gain by 15 percent and reduces Polly's gain by 25 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus will Molly receive?

A) Around 53 percent.
B) Around 59 percent.
C) Around 63 percent.
D) Around 65 percent.
E) Around 69 percent.

Question 36

Molly is interested buying Polly's antique doll house. Molly is prepared to spend up to $2,500. Polly will not sell the doll house for less than $2,000. Suppose that any failure to reach an agreement reduces Molly's gain by 15 percent and will reduce Polly's gain by 25 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus will Polly receive?

A) Around 31 percent.
B) Around 35 percent.
C) Around 37 percent.
D) Around 41 percent.
E) Around 47 percent.

Question 37

Beanie wants to purchase Cecil's house. The most that Beanie is willing to pay is$300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's and Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, how much should Beanie offer for the house?

A) An amount between $282,700 and $282,750
B) An amount between $279,950 and $280,000
C) An amount between $276,000 and $276,050
D) An amount between $274,050 and $274,100
E) An amount between $275,500 and $275,550

Question 38

Beanie wants to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's and Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Beanie receive?

A) Around 44 percent.
B) Around 46 percent.
C) Around 48 percent.
D) Around 50 percent.
E) Around 52 percent.

Question 39

Beanie wants to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's and Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Cecil receive?

A) Around 44 percent.
B) Around 46 percent.
C) Around 48 percent.
D) Around 50 percent.
E) Around 52 percent.

Question 40

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's gain by 3 percent and reduces Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, how much should Beanie offer for the house?

A) An amount between $292,300 and $292,400.
B) An amount between $284,600 and $284,700
C) An amount between $271,300 and $271,400
D) An amount between $265,300 and $265,400
E) An amount between $256,700 and $256,800

Question 41

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's gain by 3 percent and reduces Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Beanie receive?

A) Around 31 percent.
B) Around 35 percent.
C) Around 48 percent.
D) Around 56 percent.
E) Around 69 percent.

Question 42

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanie's gain by 3 percent and reduces Cecil's gain by 7 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Cecil receive?

A) Around 31 percent.
B) Around 35 percent.
C) Around 48 percent.
D) Around 56 percent.
E) Around 69 percent.

Question 43

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanies gain by 7 percent and reduces Cecil's gain by 3 percent. If there is no limit to the number of bargaining rounds, how much should Beanie offer for the house?

A) An amount between $264,200 and $264,300
B) An amount between $279,300 and $279,400
C) An amount between $285,700 and $285,800
D) An amount between $290,100 and $290,200
E) An amount between $291,700 and $291,800

Question 44

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanies gain by 7 percent and reduces Cecil's gain by 3 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Beanie receive?

A) Around 53 percent.
B) Around 44 percent.
C) Around 31 percent.
D) Around 29 percent.
E) Around 23 percent.

Question 45

Beanie wishes to purchase Cecil's house. The most that Beanie is willing to pay is $300,000. The least that Cecil is willing to accept is $250,000. Suppose that any failure to reach an agreement reduces Beanies gain by 7 percent and reduces Cecil's gain by 3 percent. If there is no limit to the number of bargaining rounds, what percentage of the bargaining surplus should Cecil receive?

A) Around 47 percent.
B) Around 56 percent.
C) Around 69 percent.
D) Around 72 percent.
E) Around 77 percent.

Question 46

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is willing to pay up to $4,000 for the tickets. Harriet will accept no less than $3,000. Suppose that any failure to reach an agreement reduces Ozzie's and Harriet's gain by 20 percent. If there is no limit to the number of bargaining rounds, how much should Ozzie offer Harriet?

A) An amount between $3,510 and $3,520
B) An amount between $3,440 and $3,450
C) An amount between $3,470 and $3,480
D) An amount between $3,550 and $3,560
E) An amount between $3,570 and $3,580

Question 47

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is willing to pay up to $4,000 for the tickets. Harriet will accept no less than $3,000. Suppose that any failure to reach an agreement reduces Ozzie's and Harriet's gain by 20 percent. If there is no limit to the number of negotiating rounds, what percentage of the surplus should Ozzie receive?

A) Around 72 percent.
B) Around 64 percent.
C) Around 56 percent.
D) Around 44 percent.
E) Around 32 percent.

Question 48

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is willing to pay up to $4,000 for the tickets. Harriet will accept no less than $3,000. Suppose that any failure to reach an agreement reduces Ozzie's and Harriet's gain by 20 percent. If there is no limit to the number of negotiating rounds, what percentage of the surplus should Harriet receive?

A) Around 72 percent.
B) Around 64 percent.
C) Around 56 percent.
D) Around 44 percent.
E) Around 32 percent.

Question 49

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is a member of "Red Sox Nation" and can hardly wait to get his hands on Harriet's season tickets. Ozzie is willing to pay up to $4,000. Failure to come to an agreement will reduce Ozzie's gain by 80 percent. Although Harriet likes baseball, she would rather go to the movies. The season tickets were a gift from here good-for-nothing son-in law. Be that as it may, the minimum amount that Harriet will accept for the tickets is $3,000. Failure to come to an agreement will reduce Harriet's gain by 5 percent. If there is no limit on the number of bargaining rounds, how much should Ozzie offer Harriet?

A) An amount between $3,950 and $4,000
B) An amount between $3,600 and $3,650
C) An amount between $3,575 and $3,625
D) An amount between $3,525 and $3,575
E) An amount between $3,400 and $3,450

Question 50

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is a member of "Red Sox Nation" and can hardly wait to get his hands on Harriet's season tickets. Ozzie is willing to pay up to $4,000. Failure to come to an agreement will reduce Ozzie's gain by 80 percent. Although Harriet likes baseball, she would rather go to the movies. The season tickets were a gift from here good-for-nothing son-in-law. Be that as it may, the minimum amount that Harriet will accept for the tickets is $3,000. Failure to come to an agreement will reduce Harriet's gain by 5 percent. If there is no limit on the number of bargaining rounds, what percentage of the bargaining surplus should Ozzie receive?

A) Around 1 percent.
B) Around 6 percent.
C) Around 8 percent.
D) Around 10 percent.
E) Around 12 percent.

Question 51

It is March and Ozzie wants to purchase Harriet's season tickets to Boston Red Sox games. Ozzie is a member of "Red Sox Nation" and can hardly wait to get his hands on Harriet's season tickets. Ozzie is willing to pay up to $4,000. Failure to come to an agreement will reduce Ozzie's gain by 80 percent. Although Harriet likes baseball, she would rather go to the movies. The season tickets were a gift from here good-for-nothing son-in-law. Be that as it may, the minimum amount that Harriet will accept for the tickets is $3,000. Failure to come to an agreement will reduce Harriet's gain by 5 percent. If there is no limit on the number of bargaining rounds, what percentage of the bargaining surplus should Harriet receive?

A) Around 88 percent.
B) Around 90 percent.
C) Around 92 percent.
D) Around 94 percent.
E) Around 99 percent.

Question 52

Suppose that management and labor are bargaining over the distribution of excess profits amounting to $200 per worker. Suppose that failure to reach an agreement an agreement reduces management's share of the surplus by 5 percent per round and reduces labor's share of the surplus by 7 percent per round. If there is an unlimited number of negotiating rounds, what percentage of the excess profits should management offer labor in the first round?

A) Around 38 percent.
B) Around 43 percent.
C) Around 57 percent.
D) Around 62 percent.
E) Around 74 percent.

Question 53

Suppose that management and labor are bargaining over the distribution of excess profits amounting to $200 per worker. Suppose that failure to reach an agreement an agreement reduces management's share of the surplus by 5 percent per round and reduces labor's share of the surplus by 7 percent per round. If there is an unlimited number of negotiating rounds, how much of the excess profits will go to the shareholders?

A) Around $76 per worker.
B) Around $86 per worker.
C) Around $114 per worker.
D) Around $124 per worker.
E) Around $148 per worker.

Question 54

Suppose that management and labor are bargaining over the distribution of excess profits amounting to $200 per worker. Suppose that failure to reach an agreement an agreement reduces management's share of the surplus by 5 percent per round and reduces labor's share of the surplus by 7 percent per round. If there is an unlimited number of negotiating rounds, how much of the excess profits will go to labor?

A) Around $76 per worker.
B) Around $86 per worker.
C) Around $114 per worker.
D) Around $124 per worker.
E) Around $148 per worker.