Deck 8: Appendix: Algebra Review
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/123
Play
Full screen (f)
Deck 8: Appendix: Algebra Review
1
To study the rate at which animals learn, a psychology student performed an experiment in which a rat was sent repeatedly through a laboratory maze. Suppose the time required for the rat to traverse the maze on the nth trial was approximately minutes. How many minutes does it take the rat to traverse the maze on the 2nd trial?
T(2) = 5 min
2
Find the points of intersection (if any) of the given pair of curves.y = x + 7 and y = 2x + 4
(3, 10)
3
Find the slope (if possible) of the line that passes through the given pair of points. (1, 0) and (18, 12)
4
Write an equation for the line with the given properties.Through (3, -1) with slope 2

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
5
An appliance manufacturer can sell refrigerators for $600 apiece. The manufacturer's total cost consists of a fixed overhead of $12,000 plus production cost of $400 per refrigerator. How many refrigerators must be sold for the manufacturer to break even?

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
6
Find the indicated limit if it exists.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
7
Decide if the given function is continuous at the specified value of x.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
8
Differentiate:

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
9
The equation of the line tangent to the graph of that passes through (1, 5) is y = 2x + 4.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
10
What is the rate of change of with respect to t when t = 42?

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
11
An equation for the tangent line to the curve at the point where x = 1 is

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
12
If , then

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
13
Find an equation for the tangent line to the curve at the point (1, -1).

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
14
Find all intervals where the derivative of the function shown below is negative. 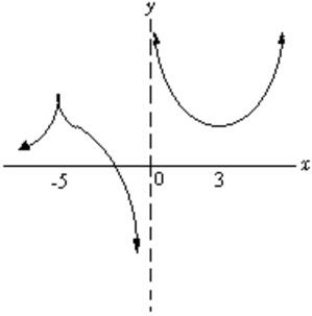


Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
15
Find the intervals of increase and decrease for Round numbers to two decimal places, if necessary.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
16
Determine where the graph of is concave up and concave down.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
17
Find all critical points of , and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
18
Find the absolute maximum and minimum of on the interval -1 x 2.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
19
Find two non-negative numbers whose sum is 12 for which the product of their squares is as large as possible.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
20
The owner of an appliance store expects to sell 600 toasters this year. Each toaster costs her $7 dollars to purchase, and each time she orders a shipment of toasters, it costs $24. In addition, it costs $4 a year to store each toaster. Assuming the toasters sell out at a uniform rate and that the owner never allows herself to run out of toasters, how many toasters should be ordered in each shipment to minimize the annual cost? (Round any fractional amounts.)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
21
Find the indicated composite function.f (5x - 4) where

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
22
Find the points of intersection (if any) of the given pair of curves.y = 7x - 8 and y = 2x - 6

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
23
Find the slope and y-intercept of the line whose equation is given.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
24
Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is + or - . where

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
25
Find the relative rate of change of f (x) with respect to x for the prescribed value x = 1.f (x) =3x3 + 2x2 - 8

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
26
The equation of the tangent line to the curve at the point (0, -2) is y = 2x - 2.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
27
Find an equation for the tangent line to the curve at the point where x = -1. Round numbers to two decimal places.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
28
Find an equation for the tangent line to the curve at the point (1, -1).

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
29
Find the intervals of increase and decrease for the function .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
30
Let . Find all critical points of f and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
31
To raise money, a service club has been collecting used bottles that it plans to deliver to a local glass company for recycling. Since the project began 90 days ago, the club has collected 45,000 pounds of glass for which the glass company currently offers 1 cent per pound. However, because bottles are accumulating faster than they can be recycled, the company plans to reduce by 1 cent each day the price it will pay for 100 pounds of used glass. Assume that the club can continue to collect bottles at the same rate and that transportation costs make more than one trip to the glass company unfeasible. What is the most advantageous time for the club to conclude its project and deliver the bottles?

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
32
Simplify:

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
33
The fraction of television sets manufactured by a certain company that are still in working condition after t years of use is approximately . What fraction can be expected to fail before 4 years of use? Round your answer to two decimal places, if necessary.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the given equation for x.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
35
An archaeologist has found a fossil in which the ratio of to is the ratio in the atmosphere. Approximately how old is the fossil? The half-life of is 5,730 years. Round to the nearest whole year.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
36
If , then

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
37
The equation of the tangent line to f (x) = ln x + 5 at x = 1 is

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
38
The equation of the tangent line to at x = e is

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
39
The function y = ln 2x is concave downward everywhere.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
40

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the following integral:

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
44
Sketch the region R and then use calculus to find the area of R. R is the region between the curve and the line y = 20x for x 0.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
45
Records indicate that t hours past midnight, the temperature at the local airport was degrees Fahrenheit. What was the average temperature at the airport between 3:00 A.M. and noon? Round your answer to one decimal place, if necessary.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
46
An investment will generate income continuously at the constant rate of $2,300 per year for 5 years. If the prevailing annual interest rate remains fixed at 11% compounded continuously, what is the present value of the investment?

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
47
Money is transferred continuously into an account at the constant rate of $1,600 per year. Assume the account earns interest at the annual rate of 5% compounded continuously. Compute the future value of the income stream over a 16 year period.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
50
After t weeks, a charity is raising money at the rate of 5,000 t ln(t + 1) dollars per week. How much money is raised during the first 10 weeks? Round to the nearest ten dollars.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the improper integral: Round to two decimal places, if necessary.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
53
A certain nuclear power plant produces radioactive waste at the rate of 500 pounds per year. The waste decays exponentially at the rate of 1.5% per year. How many pounds of radioactive waste from the plant will be present in the long run? Round to two decimal places, if necessary.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
54
is a probability density function for a particular random variable X Use integration to find

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
55
The clothes dryers at a laundromat run for 45 minutes. You arrive at the laundromat and find that all of the dryers are being used. Use an appropriate uniform density function to find the probability that a dryer chosen at random will finish its cycle within 5 minutes.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
56
Compute f (1, 5) if .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
57
Compute fx for f (x, y) = 3x5y - 8x +exy.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
58
Compute for .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
59
Let f (x, y) = x ln(1 + 2x - 5y). Find .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
60
A manufacturer with exclusive rights to a sophisticated new industrial machine is planning to sell a limited number of the machines to both foreign and domestic firms. The price the manufacturer can expect to receive for the machines will depend on the number of machines made available. (For example, if only a few of the machines are placed on the market, competitive bidding among prospective purchasers will tend to drive the price up.) It is estimated that if the manufacturer supplies x machines to the domestic market and y machines to the foreign market, the machines will sell for thousand dollars apiece at home and for thousand dollars apiece abroad. If the manufacturer can produce the machines at a cost of $45,000 apiece, how many should be supplied to each market to generate the largest possible profit?

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
61
The accompanying table lists the high-school GPA and college GPA for a number of students:
Using the best fit straight line, predict the college GPA (to one decimal place) for a student whose high school GPA was 3.5.
Using the best fit straight line, predict the college GPA (to one decimal place) for a student whose high school GPA was 3.5.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
62
Find the maximum value of f (x, y) = xy on the ellipse .

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
63
Use Lagrange multipliers to find the maximum value of f (x, y, z) = 3xyz subject to 5x + 5y + 2z = 150.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
64
Use a double integral to find the area of R.R is the region bounded by y = 5x, y = ln x, y = 0, and y = 1.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
65
Find the points of intersection (if any) of the given pair of curves.y = x + 9 and y = 2x + 4
A) (1, -4)
B) (0, 6)
C) (14, 23)
D) (5, 14)
A) (1, -4)
B) (0, 6)
C) (14, 23)
D) (5, 14)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
66
Find the slope (if possible) of the line that passes through the given pair of points. (17, 0) and (20, 5)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
67
Write an equation for the line through (3, 0) with slope 2.
A) y = 2x + 6
B) y = 2x - 6
C) y = 2x + 3
D) y = 2x - 3
A) y = 2x + 6
B) y = 2x - 6
C) y = 2x + 3
D) y = 2x - 3

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
68
Find the indicated limit if it exists.
A)
B) Does not exist
C) 4
D)
A)
B) Does not exist
C) 4
D)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
69
Decide if the given function is continuous at the specified value of x.
A) Yes, the function is continuous at x = 1.
B) No, the function is not continuous at x = 1.
A) Yes, the function is continuous at x = 1.
B) No, the function is not continuous at x = 1.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
70
Differentiate:
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
71
The equation of the line tangent to the graph of that passes through (9, 4) is y = 2x + 1.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
72
What is the rate of change of with respect to t when t = 17?
A) 21
B) -21
C)
D)
A) 21
B) -21
C)
D)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
73
An equation for the tangent line to the curve at the point where x = 1 is
A) y = 18x
B) y = 18x - 1
C) y = 18x - 17
D) y = 2x + 1
A) y = 18x
B) y = 18x - 1
C) y = 18x - 17
D) y = 2x + 1

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
74
If , then

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
75
Find the intervals of increase and decrease for the function
A) Increasing for all x
B) Decreasing for ; increasing for
C) Decreasing for ; increasing for
D) Decreasing for all x
A) Increasing for all x
B) Decreasing for ; increasing for
C) Decreasing for ; increasing for
D) Decreasing for all x

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
76
Find the intervals of increase and decrease for Round numbers to two decimal places, if necessary.
A) Increasing on x 0.50 and on x > 5, decreasing on 0.50 < x 5
B) Increasing on x < 5, decreasing on x > 5
C) Increasing on 0.50 < x 5, decreasing on x 0.50 and on x > 5
D) Increasing on x < 5 and x > 5
A) Increasing on x 0.50 and on x > 5, decreasing on 0.50 < x 5
B) Increasing on x < 5, decreasing on x > 5
C) Increasing on 0.50 < x 5, decreasing on x 0.50 and on x > 5
D) Increasing on x < 5 and x > 5

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
77
Determine where the graph of is concave down.
A) x < 1
B) x < -1
C) x > 1
D) x > -1
A) x < 1
B) x < -1
C) x > 1
D) x > -1

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
78
The second derivative test reveals that has
A) a relative minimum only.
B) a relative maximum and two relative minima.
C) neither a relative maximum nor a relative minimum.
D) a relative maximum only.
A) a relative minimum only.
B) a relative maximum and two relative minima.
C) neither a relative maximum nor a relative minimum.
D) a relative maximum only.

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
79
Find the absolute maximum of the function on the interval
A) 1
B) -1
C) 0
D)
A) 1
B) -1
C) 0
D)

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck
80
Find two non-negative numbers whose sum is 14 for which the product of their squares is as large as possible.
A) 0 and 14
B) 5 and 9
C) 7 and 7
D) 1 and 13
A) 0 and 14
B) 5 and 9
C) 7 and 7
D) 1 and 13

Unlock Deck
Unlock for access to all 123 flashcards in this deck.
Unlock Deck
k this deck


