Deck 1: Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 1: Linear Equations
1
Use back-substitution to solve the system of linear equations. 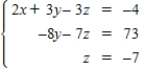
A)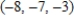
B)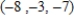
C)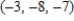
D)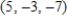
E)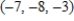
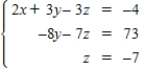
A)
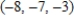
B)
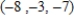
C)
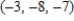
D)
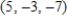
E)
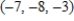
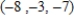
2
Solve the system of equations by using graphical methods.
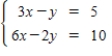
A)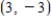
B)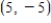
C)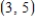
D)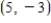
E) There are infinitely many solutions.
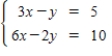
A)
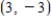
B)
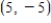
C)
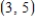
D)
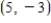
E) There are infinitely many solutions.
There are infinitely many solutions.
3
Solve the system of equations by using graphical methods.
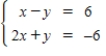
A)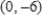
B)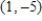
C)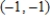
D)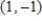
E) There is no solution to the equations.
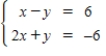
A)
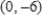
B)
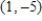
C)
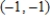
D)
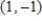
E) There is no solution to the equations.
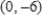
4
Solve using any method.
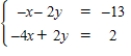
A)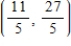
B)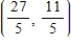
C)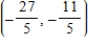
D)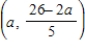 , where a is any real number
, where a is any real number
E) inconsistent
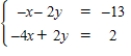
A)
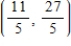
B)
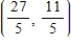
C)
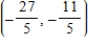
D)
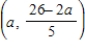 , where a is any real number
, where a is any real numberE) inconsistent

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system. 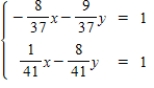
A)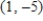
B)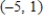
C)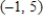
D)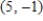
E)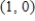
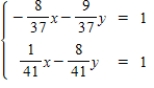
A)
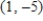
B)
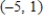
C)
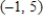
D)
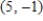
E)
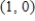

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the system of linear equations. 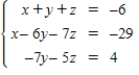
A)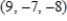
B)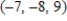
C)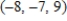
D)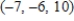
E)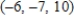
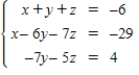
A)
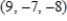
B)
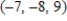
C)
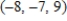
D)
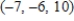
E)
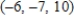

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system of linear equations. 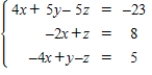
A)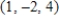
B)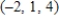
C)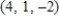
D)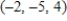
E)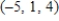
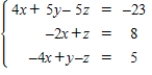
A)
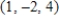
B)
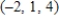
C)
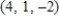
D)
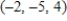
E)
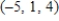

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system of linear equations. 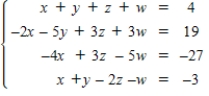
A)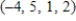
B)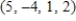
C)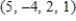
D)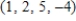
E)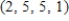
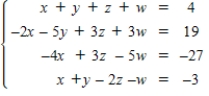
A)
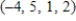
B)
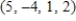
C)
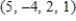
D)
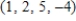
E)
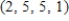

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether the matrix is in row-echelon form. If it is, determine if it is also in reduced row-echelon form. 
A) row-echelon form
B) row-echelon form and reduced row-echelon form
C) neither

A) row-echelon form
B) row-echelon form and reduced row-echelon form
C) neither

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
Find the solution set of the system of linear equations in the variables x and y (in that order) that has the following augmented matrix. 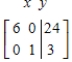
A)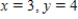
B)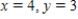
C)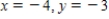
D)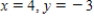
E)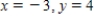
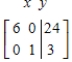
A)
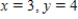
B)
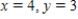
C)
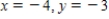
D)
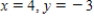
E)
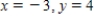

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
Write the system of linear equations represented by the augmented matrix. Then use back-substitution to solve. (Use variables x, y, and z.) 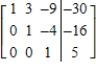
A)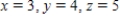
B)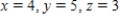
C)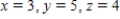
D)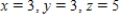
E)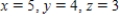
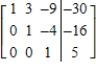
A)
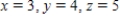
B)
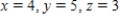
C)
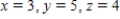
D)
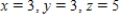
E)
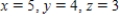

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
The given matrix is an augmented matrix representing a system of linear equations. Find the solution of the system. 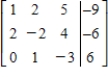
A)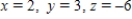
B)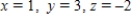
C)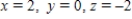
D)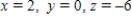
E)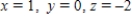
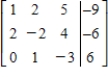
A)
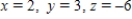
B)
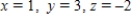
C)
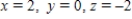
D)
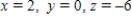
E)
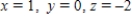

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
Use matrices to solve the system of equations (if possible). Use Gaussian elimination with back-substitution or Gauss-Jordan elimination. 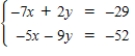
A)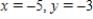
B)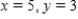
C)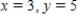
D)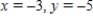
E) no solution
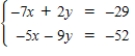
A)
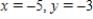
B)
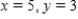
C)
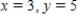
D)
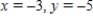
E) no solution

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Use Gaussian elimination method to solve the system of linear equations. 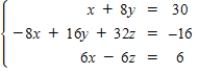
A)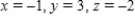
B)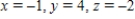
C)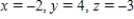
D)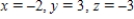
E) inconsistent system
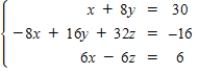
A)
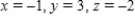
B)
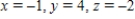
C)
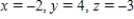
D)
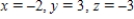
E) inconsistent system

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the following system using either Gaussian elimination with back-substitution or Gauss-Jordan elimination. If there is no solution, state that the system is inconsistent. 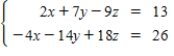
A)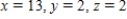
B)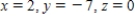
C)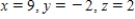
D) inconsistent system
E)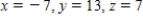
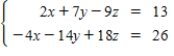
A)
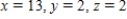
B)
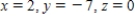
C)
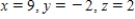
D) inconsistent system
E)
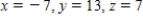

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Find the equation of the parabola 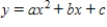 that passes through the points
that passes through the points 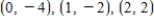 .
.
A)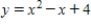
B)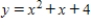
C)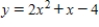
D)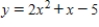
E)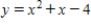
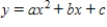 that passes through the points
that passes through the points 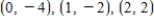 .
.A)
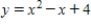
B)
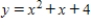
C)
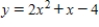
D)
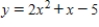
E)
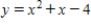

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Find the equation of the circle 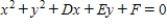 that passes through the points
that passes through the points 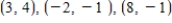 .
.
A)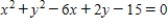
B)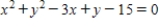
C)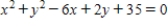
D)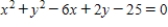
E)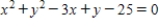
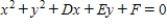 that passes through the points
that passes through the points 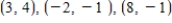 .
.A)
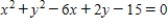
B)
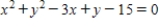
C)
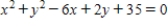
D)
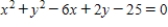
E)
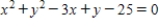

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose that the U. S. population for the years 1920, 1930, 1940, and 1950 is shown in the table below. Let x represent the number of decades since 1920. Find a cubic polynomial 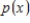 that fits these data
that fits these data 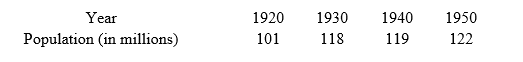
A)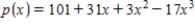
B)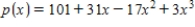
C)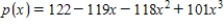
D)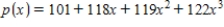
E)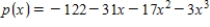
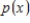 that fits these data
that fits these data 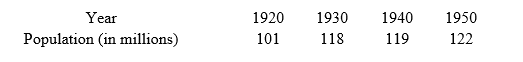
A)
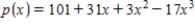
B)
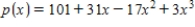
C)
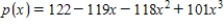
D)
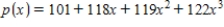
E)
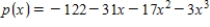

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that the U. S. population for the years 1920, 1930, 1940, and 1950 is shown in the table below. Let x represent the number of decades since 1920. Estimate the population in 1970 by using a cubic polynomial that fits these data. 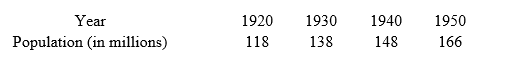
A) 448 million
B) 278 million
C) 236 million
D) 298 million
E) 210 million
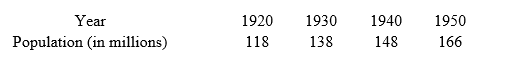
A) 448 million
B) 278 million
C) 236 million
D) 298 million
E) 210 million

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Suppose that the net profit (in millions of dollars) for Microsoft from 2000 to 2007 is shown in the table below. 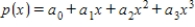
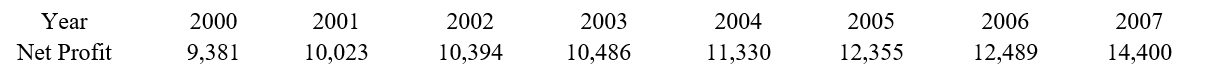
A cubic model that matches the data for the years 2001, 2003, 2005, and 2007 is to be determined where x represents the number of years since 2000. Set up a system of equations to solve for the coefficients a0, a1, a2 and a3.
A)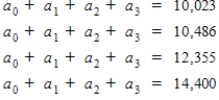
B)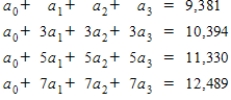
C)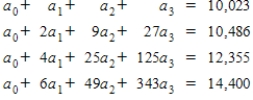
D)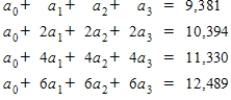
E)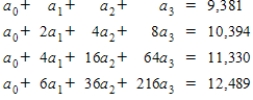
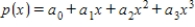
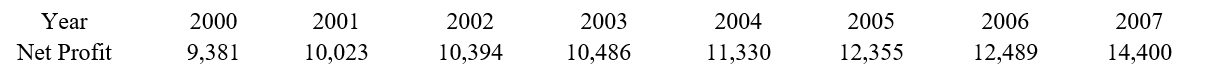
A cubic model that matches the data for the years 2001, 2003, 2005, and 2007 is to be determined where x represents the number of years since 2000. Set up a system of equations to solve for the coefficients a0, a1, a2 and a3.
A)
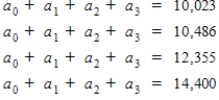
B)
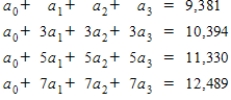
C)
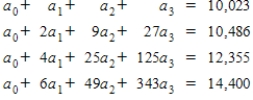
D)
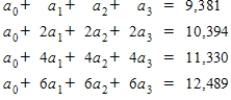
E)
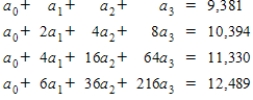

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Irrigation. An irrigation system allows water to flow in the pattern shown in the figure below. Water flows into the system at A and exits at B, C, D, and E with the amounts shown. Using the fact that at each point the water entering equals the water leaving, formulate an equation for water flow at each of the five points and solve the system.
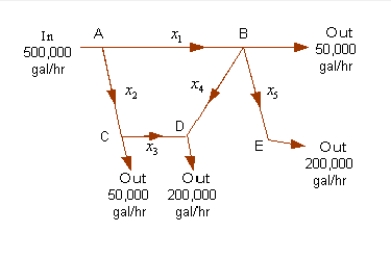
A)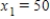 ,
, 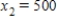 ,
, 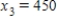 ,
, 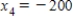 ,
, 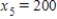 (in thousands of gallons)
(in thousands of gallons)
B)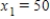 ,
, 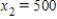 ,
, 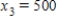 ,
, 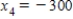 ,
, 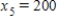 (in thousands of gallons)
(in thousands of gallons)
C)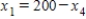 ,
, 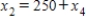 ,
, 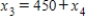 ,
, 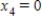 ,
, 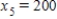 (in thousands of gallons)
(in thousands of gallons)
D)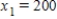 ,
, 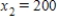 ,
, 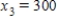 ,
, 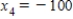 ,
, 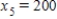 (in thousands of gallons)
(in thousands of gallons)
E)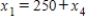 ,
, 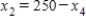 ,
, 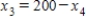 ,
, 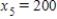 ,
, 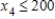 (in thousands of gallons)
(in thousands of gallons)

A)
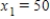 ,
, 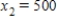 ,
, 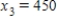 ,
, 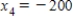 ,
, 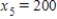 (in thousands of gallons)
(in thousands of gallons)B)
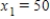 ,
, 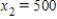 ,
, 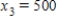 ,
, 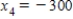 ,
, 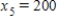 (in thousands of gallons)
(in thousands of gallons)C)
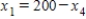 ,
, 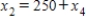 ,
, 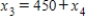 ,
, 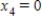 ,
, 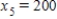 (in thousands of gallons)
(in thousands of gallons)D)
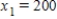 ,
, 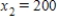 ,
, 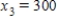 ,
, 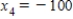 ,
, 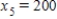 (in thousands of gallons)
(in thousands of gallons)E)
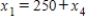 ,
, 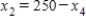 ,
, 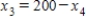 ,
, 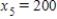 ,
, 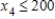 (in thousands of gallons)
(in thousands of gallons)
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
Traffic flow. In the analysis of traffic flow, a certain city estimates the following situation for the "square" of its downtown district. In the following figure, the arrows indicate the flow of traffic. If x1 represents the number of cars traveling between intersections A and B, x2 represents the number of cars traveling between B and C, x3 the number between C and D, and x4 the number between D and A, we can formulate equations based on the principle that the number of vehicles entering an intersection equals the number leaving it. That is, for intersection A we obtain
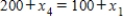
Formulate equations for the traffic at B, C, and D. Solve the system of these four equations.
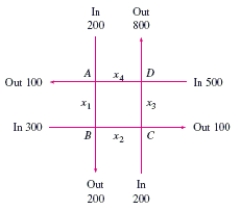
A)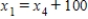 ,
, 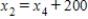 ,
, 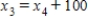 ,
, 
B)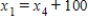 ,
, 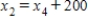 ,
, 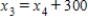 ,
, 
C)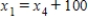 ,
, 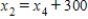 ,
, 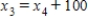 ,
, 
D)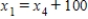 ,
, 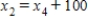 ,
,  ,
, 
E)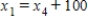 ,
, 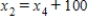 ,
, 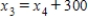 ,
, 
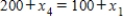
Formulate equations for the traffic at B, C, and D. Solve the system of these four equations.

A)
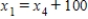 ,
, 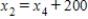 ,
, 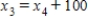 ,
, 
B)
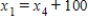 ,
, 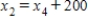 ,
, 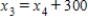 ,
, 
C)
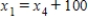 ,
, 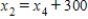 ,
, 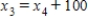 ,
, 
D)
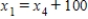 ,
, 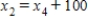 ,
,  ,
, 
E)
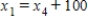 ,
, 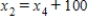 ,
, 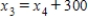 ,
, 

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
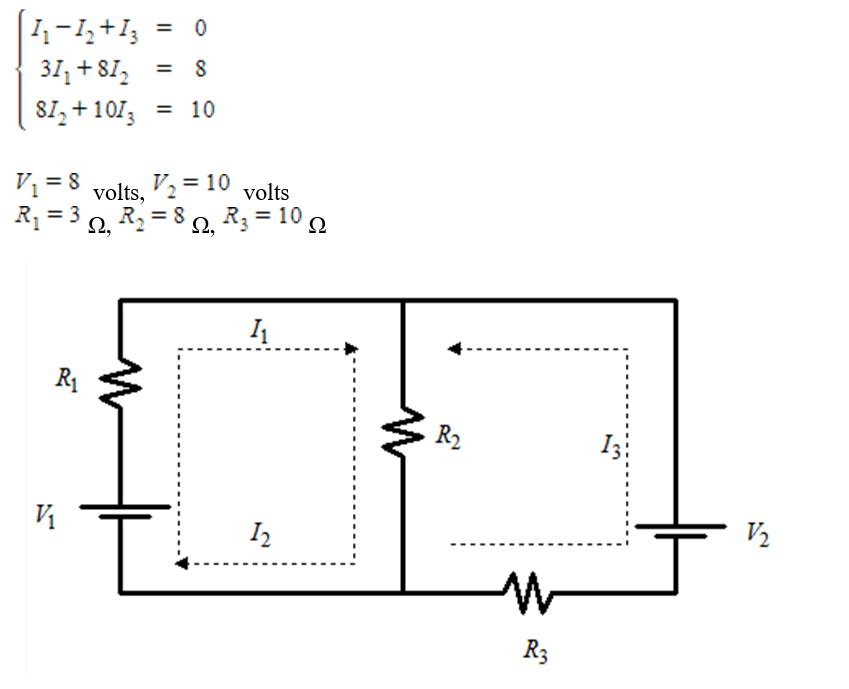
Applying Kirchhoff's Laws to the electrical network in the figure, the currents I1, I2, and I3 are the solution of the system
A)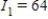 amperes;
amperes; 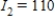 amperes;
amperes; 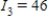 amperes
amperes
B)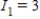 amperes;
amperes; 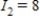 amperes;
amperes; 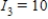 amperes
amperes
C)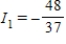 amperes;
amperes; 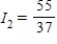 amperes;
amperes; 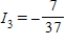 amperes
amperes
D)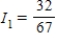 amperes;
amperes; 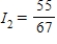 amperes;
amperes; 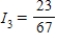 amperes
amperes
E)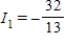 amperes;
amperes; 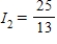 amperes;
amperes; 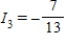 amperes
amperes

A)
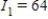 amperes;
amperes; 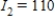 amperes;
amperes; 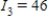 amperes
amperesB)
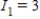 amperes;
amperes; 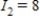 amperes;
amperes; 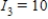 amperes
amperesC)
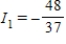 amperes;
amperes; 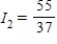 amperes;
amperes; 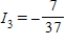 amperes
amperesD)
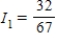 amperes;
amperes; 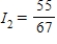 amperes;
amperes; 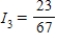 amperes
amperesE)
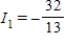 amperes;
amperes; 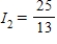 amperes;
amperes; 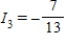 amperes
amperes
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Write the partial fraction decomposition of the rational expression.
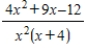
A)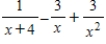
B)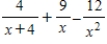
C)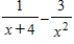
D)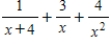
E)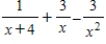
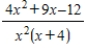
A)
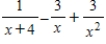
B)
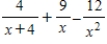
C)
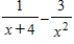
D)
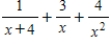
E)
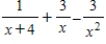

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Use a system of equations to write the partial fraction decomposition of the rational expression 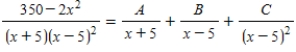 .
.
Then solve the system using matrices.
A)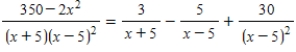
B)
C)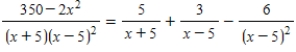
D)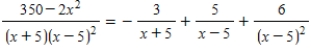
E)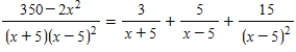
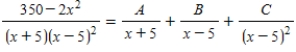 .
. Then solve the system using matrices.
A)
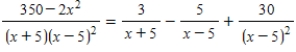
B)

C)
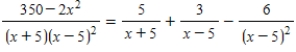
D)
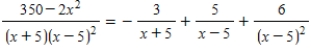
E)
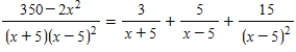

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck


