Deck 5: Linear Inequalities and Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/26
Play
Full screen (f)
Deck 5: Linear Inequalities and Linear Programming
1
Graph the inequality:
-y < - 2
A)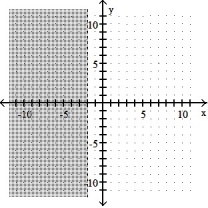
B)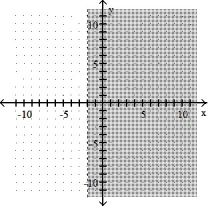
C)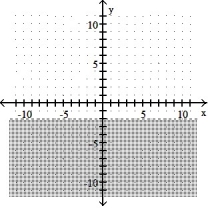
D)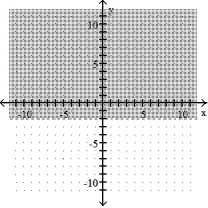
-y < - 2

A)

B)

C)

D)


2
Graph the inequality:
-2x + y 1
A)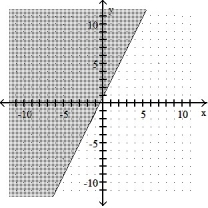
B)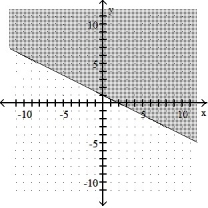
C)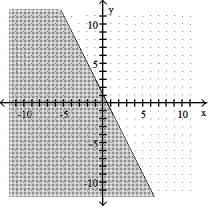
D)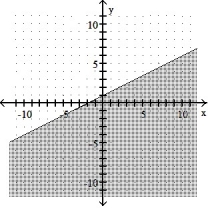
-2x + y 1

A)

B)

C)

D)


3
Graph the inequality:
-x + 5y 2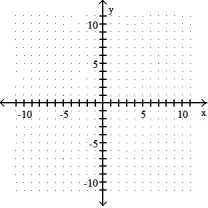
A)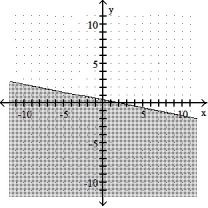
B)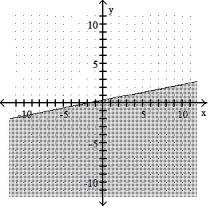
C)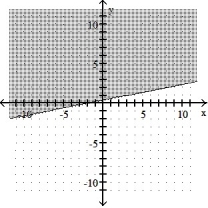
D)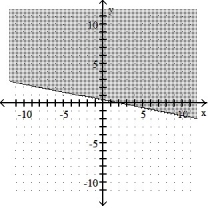
-x + 5y 2

A)

B)

C)

D)


4
Graph the inequality:
-4x - 2y 8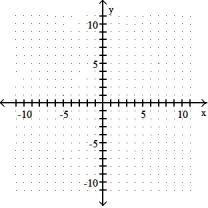
A)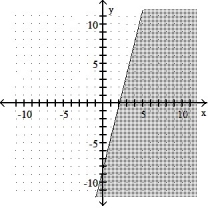
B)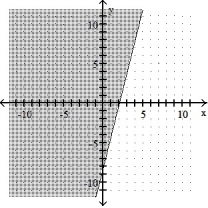
C)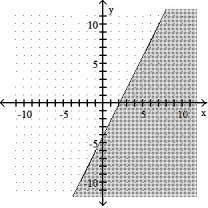
D)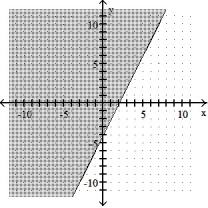
-4x - 2y 8

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-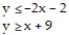
A) Unbounded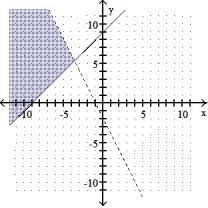
B) Unbounded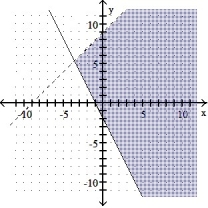
C) Unbounded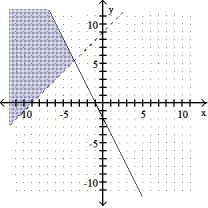
D) Unbounded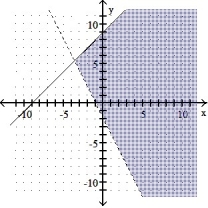
-
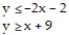

A) Unbounded

B) Unbounded

C) Unbounded

D) Unbounded


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-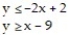
A) Bounded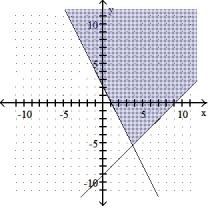
B) Unbounded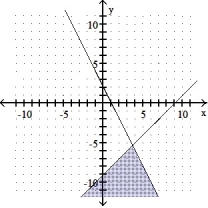
C) Bounded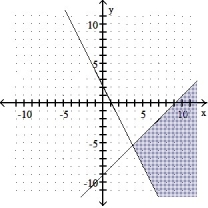
D) Unbounded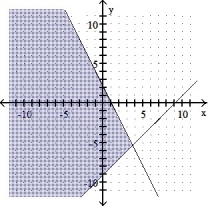
-
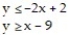

A) Bounded

B) Unbounded

C) Bounded

D) Unbounded


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
7
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-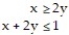
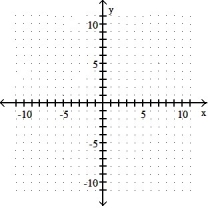
A) Unbounded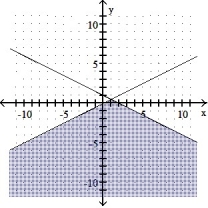
B) Unbounded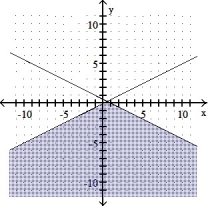
C) Bounded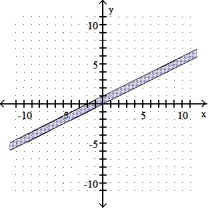
D) Unbounded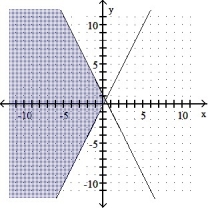
-
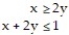

A) Unbounded

B) Unbounded

C) Bounded

D) Unbounded


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
8
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-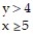
A) Unbounded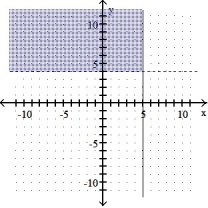
B) Bounded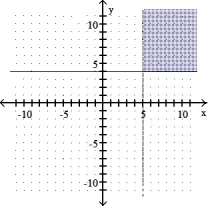
C) Unbounded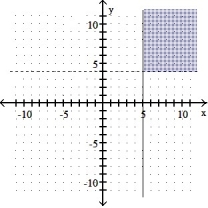
D) Bounded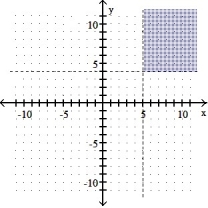
-
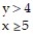

A) Unbounded

B) Bounded

C) Unbounded

D) Bounded


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-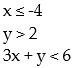
A) Bounded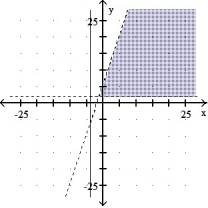
B) Unbounded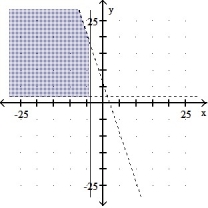
C) Bounded
D) Unbounded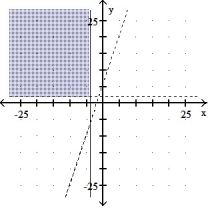
-
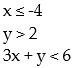
A) Bounded

B) Unbounded

C) Bounded

D) Unbounded


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
10
Find the coordinates of the corner points of the solution region for: 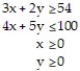
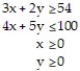

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
11
Formulate the following problem as a linear programming problem (DO NOT SOLVE).A company which produces three kinds of spaghetti sauce has two plants. The East plant produces 3,500 jars of plain sauce, 6,500 jars of sauce with mushrooms, and 3,000 jars of hot spicy sauce per day. The West plant produces 2,500 jars of plain sauce, 2,000 jars of sauce with mushrooms, and 1,500 jars of hot spicy sauce per day. The cost to operate the East plant is $8,500 per day and the cost to operate the West plant is $9,500 per day. How many days should each plant operate to minimize cost and to fill an order for at least 8,000 jars of plain sauce, 9,000 jars of sauce with mushrooms, and 6,000 jars of hot spicy sauce? (Let 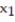 equal the number of days East plant should operate and
equal the number of days East plant should operate and 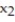 the number of days West plant should operate.)
the number of days West plant should operate.)
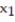 equal the number of days East plant should operate and
equal the number of days East plant should operate and 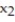 the number of days West plant should operate.)
the number of days West plant should operate.)
Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
12
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A small accounting firm prepares tax returns for two types of customers: individuals and small businesses. Data is collected during an interview. A computer system is used to produce the tax return. It takes 2.5 hours to enter data into the computer for an individual tax return and 3 hours to enter data for a small business tax return. There is a maximum of 40 hours per week for data entry. It takes 20 minutes for the computer to process an individual tax return and 30 minutes to process a small business tax return. The computer is available for a maximum of 900 minutes per week. The accounting firm makes a profit of $125 on each individual tax return processed and a profit of $210 on each small business tax return processed. How many of each type of tax return should the firm schedule each week in order to maximize its profit? (Let 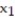 equal the number of individual tax returns and
equal the number of individual tax returns and 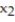 the number of small business tax returns.)
the number of small business tax returns.)
Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the maximum profit occurs for the given objective function.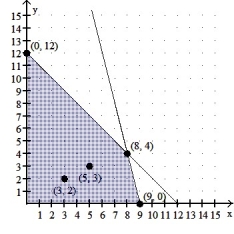
 equal the number of individual tax returns and
equal the number of individual tax returns and 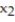 the number of small business tax returns.)
the number of small business tax returns.)Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the maximum profit occurs for the given objective function.


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
13
Use graphical methods to solve the linear programming problem:
-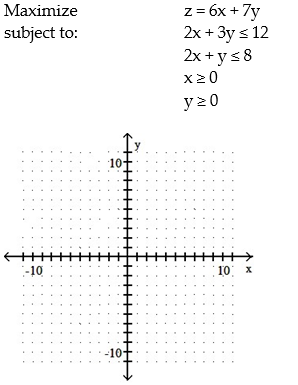
A) Maximum of 24 when x = 4 and y = 0
B) Maximum of 32 when x = 3 and y = 2
C) Maximum of 52 when x = 4 and y = 4
D) Maximum of 32 when x = 2 and y = 3
-

A) Maximum of 24 when x = 4 and y = 0
B) Maximum of 32 when x = 3 and y = 2
C) Maximum of 52 when x = 4 and y = 4
D) Maximum of 32 when x = 2 and y = 3

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
14
Use graphical methods to solve the linear programming problem:
-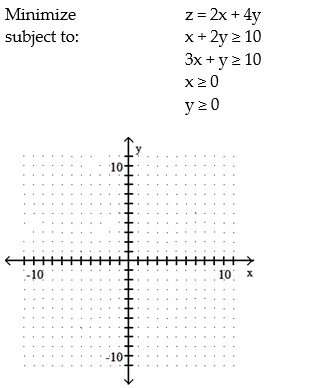
A) Minimum of 0 when x = 0 and y = 0
B) Minimum of 20 when x = 10 and y = 0
C) Minimum of 20 when x = 2 and y = 4
D) Minimum of 20 when x = 2 and y = 4, as well as when x = 10 and y = 0, and all points in between
-

A) Minimum of 0 when x = 0 and y = 0
B) Minimum of 20 when x = 10 and y = 0
C) Minimum of 20 when x = 2 and y = 4
D) Minimum of 20 when x = 2 and y = 4, as well as when x = 10 and y = 0, and all points in between

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
15
Use graphical methods to solve the linear programming problem:
-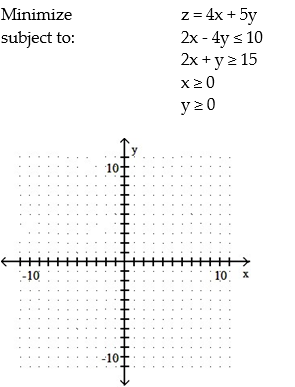
A) Minimum of 75 when x = 0 and y = 15
B) Minimum of 33 when x = 7 and y = 1
C) Minimum of 39 when x = 1 and y = 7
D) Minimum of 20 when x = 5 and y = 0
-

A) Minimum of 75 when x = 0 and y = 15
B) Minimum of 33 when x = 7 and y = 1
C) Minimum of 39 when x = 1 and y = 7
D) Minimum of 20 when x = 5 and y = 0

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
16
Use graphical methods to solve the linear programming problem:
-
A) Maximum of 96 when x = 9 and y = 2
B) Maximum of 92 when x = 4 and y = 5
C) Maximum of 100 when x = 8 and y = 3
D) Maximum of 120 when x = 3 and y = 8P
-

A) Maximum of 96 when x = 9 and y = 2
B) Maximum of 92 when x = 4 and y = 5
C) Maximum of 100 when x = 8 and y = 3
D) Maximum of 120 when x = 3 and y = 8P

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
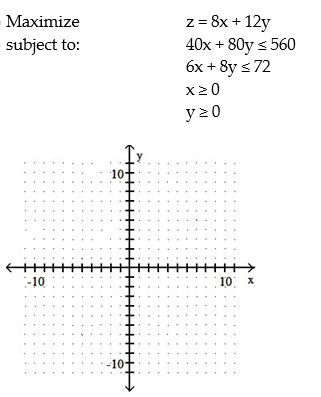
17
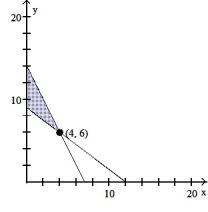
Solve the following linear programming problem by determining the feasible region on the graph below and testing the corner points:
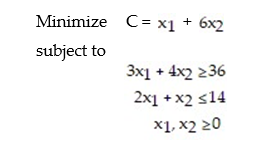
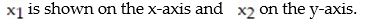
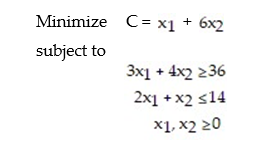

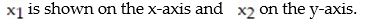

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
18
The corner points for the bounded feasible region determined by the system of inequalities: 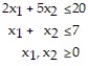 are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function: 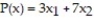
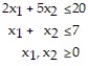 are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 4), B = (5, 2) and C = (7, 0). Find the optimal solution for the objective profit function: 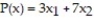

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
19
The corner points for the bounded feasible region determined by the system of inequalities: 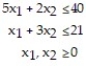 are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function: 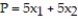
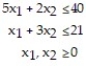 are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function:
are O = (0, 0), A = (0, 7), B = (6, 5) and C = (8, 0). Find the optimal solution for the objective profit function: 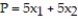

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
20
Using a graphing calculator as needed, 
Give the answer to two decimal places.

Give the answer to two decimal places.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
21
Using a graphing calculator as needed, 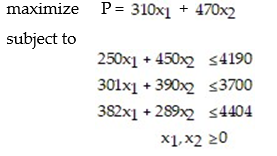
Give the answer to two decimal places.
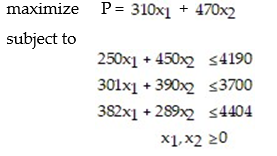
Give the answer to two decimal places.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
22
Refer to the following system of linear inequalities associated with a linear programming problem:
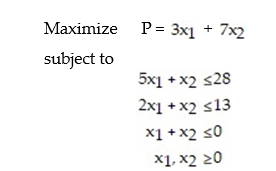 (A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(B) Determine the number of basic variables associated with this system.
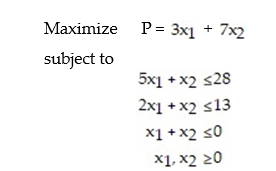 (A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations.
(A) Determine the number of slack variable that must be introduced to form a system of problem constraint equations. (B) Determine the number of basic variables associated with this system.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
23
Use graphical methods to solve the linear programming problem:
-A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100. The camp can accommodate up to 45 staff members and needs at least 30 to run properly. They must have at least 10 aides, and may have up to 3 aides for every 2 counselors. How many counselors and how many aides should the camp hire to minimize cost?
A) 35 counselors and 10 aides
B) 18 counselors and 12 aides
C) 12 counselors and 18 aides
D) 27 counselors and 18 aides
-A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100. The camp can accommodate up to 45 staff members and needs at least 30 to run properly. They must have at least 10 aides, and may have up to 3 aides for every 2 counselors. How many counselors and how many aides should the camp hire to minimize cost?
A) 35 counselors and 10 aides
B) 18 counselors and 12 aides
C) 12 counselors and 18 aides
D) 27 counselors and 18 aides

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
24
The Old-World Class Ring Company designs and sells two types of rings: the BRASS and the GOLD. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one BRASS ring and 2 man-hours to make one GOLD ring. How many of each type of ring should be made daily to maximize the company's profit, if the profit on a BRASS ring is $40 and on an GOLD ring is $30?
A) 14 BRASS and 14 GOLD
B) 12 BRASS and 12 GOLD
C) 14 BRASS and 10 GOLD
D) 10 BRASS and 14 GOLD
A) 14 BRASS and 14 GOLD
B) 12 BRASS and 12 GOLD
C) 14 BRASS and 10 GOLD
D) 10 BRASS and 14 GOLD

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
25
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company produces two types of machine dies, part A and part B. Part A requires 6 hours of casting time and 4 hours of firing time. Part B requires 8 hours of casting time and 3 hours of firing time. The maximum number of hours per week available for casting and firing are 85 and 70, respectively. The company makes a $2.00 profit on each part A that it produces, and a $6.00 profit on each part B that it produces. How many of each type should the company produce each week in order to maximize its profit? (Let 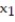 equal the number of A parts and
equal the number of A parts and 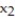 equal the number of B parts produced each week.)
equal the number of B parts produced each week.)
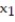 equal the number of A parts and
equal the number of A parts and 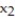 equal the number of B parts produced each week.)
equal the number of B parts produced each week.)
Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
26
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A dietitian can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. Each ounce of chicken contains 13 units of protein and 24 units of carbohydrates. Each ounce of potatoes contains 5 units of protein and 35 units of carbohydrates. The minimum daily requirements for the patients under the dietitian's care are 45 units of protein and 58 units of carbohydrates. How many ounces of each type of food should the dietitian purchase for each patient so as to minimize costs and at the same time insure the minimum daily requirements of protein and carbohydrates? (Let 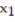 equal the number of ounces of chicken and
equal the number of ounces of chicken and 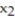 the number of ounces of potatoes purchased per patient.)
the number of ounces of potatoes purchased per patient.)
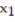 equal the number of ounces of chicken and
equal the number of ounces of chicken and 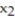 the number of ounces of potatoes purchased per patient.)
the number of ounces of potatoes purchased per patient.)
Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck


