Deck 14: Applications of Partial Derivatives
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/67
Play
Full screen (f)
Deck 14: Applications of Partial Derivatives
1
Find the critical points of f(x, y) = 3x2 - 2xy + 2y2 - 10x + 1.
A) (2, 1)
B) (1, 1)
C) (0, 0)
D) (1, -1) and (-1, 1)
E) (2, 1) and (1, 2)
A) (2, 1)
B) (1, 1)
C) (0, 0)
D) (1, -1) and (-1, 1)
E) (2, 1) and (1, 2)
(2, 1)
2
Find the critical points of f(x, y) = ln (x2 + y2 + 4x - 4y + 8).
A) (-2, 2)
B) (2, -2)
C) (-2, 2) and (2, -2)
D) (-2, 2), (2, -2), and (0, 0)
E) There are no critical points.
A) (-2, 2)
B) (2, -2)
C) (-2, 2) and (2, -2)
D) (-2, 2), (2, -2), and (0, 0)
E) There are no critical points.
There are no critical points.
3
Find all critical points of f(x) = 2x3y -4x3 + 6y3 -18y + 19.
A) (0, 1), (0, - 1), and (-9, 2)
B) only (-3, 2)
C) only (3, 2)
D) (0, 1), (0, -1), and (-3, 2)
E) only (0, 1) and (-3, 2)
A) (0, 1), (0, - 1), and (-9, 2)
B) only (-3, 2)
C) only (3, 2)
D) (0, 1), (0, -1), and (-3, 2)
E) only (0, 1) and (-3, 2)
(0, 1), (0, -1), and (-3, 2)
4
Find and classify the critical points of the function f(x, y) = x sin y.
A) local maxima at (0, n ) for even integers n, local minimum at (0, n ) for odd integers n
B) local minima at (0, n ) for even integers n, local maximum at (0, n ) for odd integers n
C) saddle points at all points (0, n ) for integers n
D) only critical point is (0, 0), a saddle point
E) local minima at (0, n ) for nonzero integers n, saddle point at (0, 0)
A) local maxima at (0, n ) for even integers n, local minimum at (0, n ) for odd integers n
B) local minima at (0, n ) for even integers n, local maximum at (0, n ) for odd integers n
C) saddle points at all points (0, n ) for integers n
D) only critical point is (0, 0), a saddle point
E) local minima at (0, n ) for nonzero integers n, saddle point at (0, 0)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
5
Find and classify the critical points of the function f(x, y) = 2y3 - 3x2 - 3xy + 9x.
A) local minimum at (2, -1), saddle point at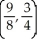
B) local maximum at (2, -1), saddle point at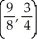
C) saddle point at (2, -1), local maximum at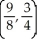
D) saddle point at (2, -1), local minimum at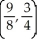
E) saddle point at (2, -1) and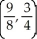
A) local minimum at (2, -1), saddle point at

B) local maximum at (2, -1), saddle point at

C) saddle point at (2, -1), local maximum at

D) saddle point at (2, -1), local minimum at

E) saddle point at (2, -1) and


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
6
Find and classify all critical points for the function f(x, y) = 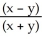 .
.
A) (1, 0); minimum
B) (-1, 0); maximum
C) (0, 0); minimum
D) (0, 0); saddle
E) There are no critical points.
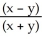 .
.A) (1, 0); minimum
B) (-1, 0); maximum
C) (0, 0); minimum
D) (0, 0); saddle
E) There are no critical points.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
7
Find and classify all critical points for the function f(x, y) = x3 - 12xy2 + y3 + 45y.
A) (2, 1) and (-2, -1) are saddle points
B) (2, 1), (2, -1), (-2, 1), and (-2, -1) are saddle points
C) (2, 1) is a local maximum and (-2, -1) is a local minimum
D) (2, -1) and (-2, 1) are saddle points
E) There are no critical points.
A) (2, 1) and (-2, -1) are saddle points
B) (2, 1), (2, -1), (-2, 1), and (-2, -1) are saddle points
C) (2, 1) is a local maximum and (-2, -1) is a local minimum
D) (2, -1) and (-2, 1) are saddle points
E) There are no critical points.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
8
Find the maximum and minimum values of f(x, y) = (x - y) 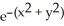 .
.
A) maximum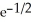 , minimum 0
, minimum 0
B) maximum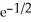 , minimum
, minimum 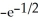
C) maximum
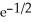 , minimum -
, minimum - 
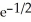
D) maximum 2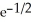 , minimum 0
, minimum 0
E) maximum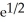 , minimum -
, minimum - 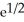
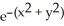 .
.A) maximum
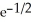 , minimum 0
, minimum 0B) maximum
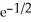 , minimum
, minimum 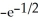
C) maximum

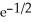 , minimum -
, minimum - 
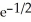
D) maximum 2
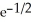 , minimum 0
, minimum 0E) maximum
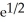 , minimum -
, minimum - 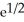

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
9
Find and classify all critical points for the function f(x, y) = 2y3 + 3y2 - 12y -x2 + 2x.
A) (1, -2) local maximum; (1, 1) local minimum
B) (1, -2) local maximum; (1, 1) saddle point
C) (1, -2) local maximum; (1, 1) local maximum
D) (1, -2) local minimum; (1, 1) local minimum
E) (-1, 2) saddle point; (1, 1) saddle point
A) (1, -2) local maximum; (1, 1) local minimum
B) (1, -2) local maximum; (1, 1) saddle point
C) (1, -2) local maximum; (1, 1) local maximum
D) (1, -2) local minimum; (1, 1) local minimum
E) (-1, 2) saddle point; (1, 1) saddle point

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
10
A rectangular box with no top has given surface area S. Find the length, width, and height of the box if the volume is as large as possible.
A) length = width =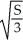 , height =
, height = 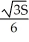
B) length = width =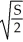 , height =
, height = 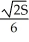
C) length = width = , height =
, height = 
D) length = width =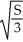 , height =
, height = 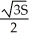
E) length = width =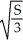 , height =
, height = 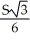
A) length = width =
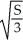 , height =
, height = 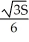
B) length = width =
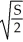 , height =
, height = 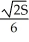
C) length = width =
 , height =
, height = 
D) length = width =
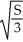 , height =
, height = 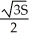
E) length = width =
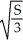 , height =
, height = 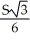

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
11
Find and classify the critical points of the following function: f(x, y) = 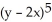 + 30x3 - 15y3.
+ 30x3 - 15y3.
A) saddle points are ( , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, 3) and minimum at (-3, -3)
), maximum at (3, 3) and minimum at (-3, -3)
B) saddle points are (0, 0), ( , -
, -  ) and (-
) and (-  ,
,  ), minimum at (3, 3) and maximum at (-3, -3)
), minimum at (3, 3) and maximum at (-3, -3)
C) saddle points are (0, 0), ( , -
, -  ), (-
), (-  ,
,  ), (3, 3), and (-3, -3)
), (3, 3), and (-3, -3)
D) saddle points are (0, 0), ( , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, 3) and minimum at (-3, -3)
), maximum at (3, 3) and minimum at (-3, -3)
E) saddle points are (0, 0), ( , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, -3) and minimum at (-3, 3)
), maximum at (3, -3) and minimum at (-3, 3)
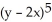 + 30x3 - 15y3.
+ 30x3 - 15y3.A) saddle points are (
 , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, 3) and minimum at (-3, -3)
), maximum at (3, 3) and minimum at (-3, -3)B) saddle points are (0, 0), (
 , -
, -  ) and (-
) and (-  ,
,  ), minimum at (3, 3) and maximum at (-3, -3)
), minimum at (3, 3) and maximum at (-3, -3)C) saddle points are (0, 0), (
 , -
, -  ), (-
), (-  ,
,  ), (3, 3), and (-3, -3)
), (3, 3), and (-3, -3)D) saddle points are (0, 0), (
 , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, 3) and minimum at (-3, -3)
), maximum at (3, 3) and minimum at (-3, -3)E) saddle points are (0, 0), (
 , -
, -  ) and (-
) and (-  ,
,  ), maximum at (3, -3) and minimum at (-3, 3)
), maximum at (3, -3) and minimum at (-3, 3)
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
12
Find and classify all critical points of f(x,y,z) = x3 + xz2 + 3x2 + y2 + 2z2 - 9x - 2y -10.
A) local minimum at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0) and saddle point at (1, 1, 0)
B) local minimum at (-2, 1, 3), (-2, 1, -3) and local maximum at (-3, 1, 0), (1, 1, 0)
C) local minimum at (1, 1, 0 ) and saddle point at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0)
D) local maximum at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0) and saddle point at (1, 1, 0)
E) local minimum at (-2, 1, 3) , (-3, 1, 0), local maximum at (1, 1, 0), and saddle point at (-2, 1, -3)
A) local minimum at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0) and saddle point at (1, 1, 0)
B) local minimum at (-2, 1, 3), (-2, 1, -3) and local maximum at (-3, 1, 0), (1, 1, 0)
C) local minimum at (1, 1, 0 ) and saddle point at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0)
D) local maximum at (-2, 1, 3), (-2, 1, -3), (-3, 1, 0) and saddle point at (1, 1, 0)
E) local minimum at (-2, 1, 3) , (-3, 1, 0), local maximum at (1, 1, 0), and saddle point at (-2, 1, -3)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
13
If a function f(x,y) has a local or absolute extreme value at the point (x0, y0) in its domain, then (x0, y0) must be either a critical point of f, a singular point of f, or a boundary point of the domain of f.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose the critical points of f(x,y) = 2x3 - 15x2 + 24x - y2 - 6y + 1 occur at the points(1, -3) and (4, -3).Then the function f has:
A) saddle points at (1, -3) and (4, -3)
B) a local minimum at (4, - 3) and a saddle point at (1, -3)
C) a local maximum at (1, - 3) and a saddle point at (4, - 3)
D) a local maximum at (4, -3) and a saddle point at (1, -3)
E) a local maximum at (4, -3) and a local minimum at (1, -3)
A) saddle points at (1, -3) and (4, -3)
B) a local minimum at (4, - 3) and a saddle point at (1, -3)
C) a local maximum at (1, - 3) and a saddle point at (4, - 3)
D) a local maximum at (4, -3) and a saddle point at (1, -3)
E) a local maximum at (4, -3) and a local minimum at (1, -3)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that a function f(x,y) has a critical point (a, b) at an interior point in its domain and that f has continuous second order partials in a neighbourhood of (a, b).
If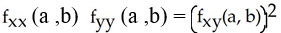 , then f has no local extremum at (a, b).
, then f has no local extremum at (a, b).
If
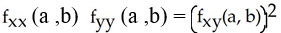 , then f has no local extremum at (a, b).
, then f has no local extremum at (a, b). 
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
16
A closed rectangular container of volume 96 cubic metres is to be made from three different materials.The top and the bottom of the container are to be made from a material that costs $4 per square metre, two parallel sides (say left and right) are to be made from a material that costs $3 per square metre, and the other two parallel sides (front and back) are to be made from a material that costs $1 per square metre.Let x and y be the dimensions of the base of the container and z be its height in metres.(i) Express the total cost of the container (in dollars) as a function of x and y.(ii) Find dimensions of the most economical container and how much it costs.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
17
Find the absolute maximum and minimum values of f(x, y) = y2 - y - x - 5 on the square0 x 1, 0 y 1.
A) maximum 0, minimum -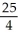
B) maximum -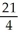 , minimum -
, minimum - 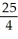
C) maximum -5, minimum -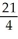
D) maximum -5, minimum -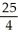
E) maximum -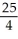 , minimum -5
, minimum -5
A) maximum 0, minimum -
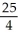
B) maximum -
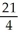 , minimum -
, minimum - 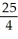
C) maximum -5, minimum -
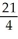
D) maximum -5, minimum -
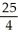
E) maximum -
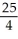 , minimum -5
, minimum -5
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
18
Find the absolute maximum and minimum of f(x, y) = 4x2 + 2xy - 3y2 on the unit square0 x 1, 0 y 1.
A) maximum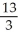 , minimum -3
, minimum -3
B) maximum 4, minimum -3
C) maximum 4, minimum 0
D) maximum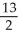 , minimum -4
, minimum -4
E) maximum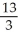 , minimum 0
, minimum 0
A) maximum
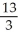 , minimum -3
, minimum -3B) maximum 4, minimum -3
C) maximum 4, minimum 0
D) maximum
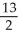 , minimum -4
, minimum -4E) maximum
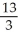 , minimum 0
, minimum 0
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
19
Find the absolute maximum and minimum values of f(x, y) = 4(x - x2) sin( y) on the rectangle 0 x 1, 0 y 2 and the points where they are assumed.
A) maximum 1 at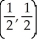 , minimum 0 at
, minimum 0 at 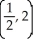
B) maximum 2 at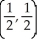 , minimum -2 at
, minimum -2 at 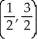
C) maximum 1 at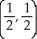 , minimum -1 at
, minimum -1 at 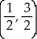
D) maximum 1 at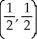 , minimum 0 at (0, 0), (1, 0), (0, 2), and (1, 2)
, minimum 0 at (0, 0), (1, 0), (0, 2), and (1, 2)
E) maximum 1 at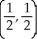 , minimum 0 at
, minimum 0 at 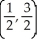
A) maximum 1 at
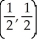 , minimum 0 at
, minimum 0 at 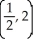
B) maximum 2 at
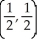 , minimum -2 at
, minimum -2 at 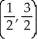
C) maximum 1 at
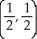 , minimum -1 at
, minimum -1 at 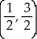
D) maximum 1 at
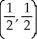 , minimum 0 at (0, 0), (1, 0), (0, 2), and (1, 2)
, minimum 0 at (0, 0), (1, 0), (0, 2), and (1, 2)E) maximum 1 at
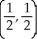 , minimum 0 at
, minimum 0 at 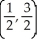

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
20
Find the absolute maximum and minimum values of the linear function f(x, y) = -2x + y - 10 on the polygon 0 x 2, 0 y 2, y - x 1.
A) maximum -9, minimum -14
B) maximum -9, minimum -12
C) maximum -8, minimum -12
D) maximum -8, minimum -15
E) maximum -9, minimum -10
A) maximum -9, minimum -14
B) maximum -9, minimum -12
C) maximum -8, minimum -12
D) maximum -8, minimum -15
E) maximum -9, minimum -10

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
21
Find the absolute maximum and minimum values of f(x, y) = x2 - 3x + y2 - 3y + 5 on the triangle bounded by x = 0, y = 0, and x + y = 2.
A) maximum 5, minimum 1
B) maximum 5, minimum 0
C) maximum 6, minimum -1
D) maximum 6, minimum 0
E) maximum 5, minimum
A) maximum 5, minimum 1
B) maximum 5, minimum 0
C) maximum 6, minimum -1
D) maximum 6, minimum 0
E) maximum 5, minimum


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
22
Find the absolute maximum and minimum values of f(x, y, z) = xyz(1 - x2 - y2 - z2) on the tetrahedron bounded by x = 0, y = 0, z = 0, and x + y + z = 2.
A) maximum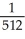 , minimum 0
, minimum 0
B) maximum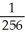 , minimum 0
, minimum 0
C) maximum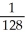 , minimum 0
, minimum 0
D) maximum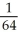 , minimum 0
, minimum 0
E) none of the above
A) maximum
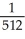 , minimum 0
, minimum 0B) maximum
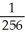 , minimum 0
, minimum 0C) maximum
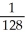 , minimum 0
, minimum 0D) maximum
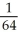 , minimum 0
, minimum 0E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
23
Find the absolute maximum and minimum values of f(x, y) = xy on the disk x2 + y2 1.
A) maximum 1, minimum -1
B) maximum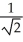 , minimum -
, minimum - 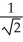
C) maximum , minimum -
, minimum - 
D) maximum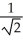 , minimum 0
, minimum 0
E) none of the above
A) maximum 1, minimum -1
B) maximum
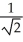 , minimum -
, minimum - 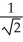
C) maximum
 , minimum -
, minimum - 
D) maximum
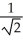 , minimum 0
, minimum 0E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
24
Find the absolute maximum and minimum values of f(x, y) = 2 - x2 - 4y on the diskx2 + y2 9.
A) maximum 16, minimum -14
B) maximum 10, minimum -13
C) maximum 14, minimum -11
D) maximum 12, minimum -10
E) none of the above
A) maximum 16, minimum -14
B) maximum 10, minimum -13
C) maximum 14, minimum -11
D) maximum 12, minimum -10
E) none of the above

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
25
Find the absolute maximum and minimum values of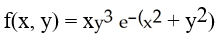 on the semi-infinite strip 0 ≤ x < ∞, -1 ≤ y ≤ 2, if these extreme values exist.
on the semi-infinite strip 0 ≤ x < ∞, -1 ≤ y ≤ 2, if these extreme values exist.
A) maximum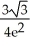 , minimum -
, minimum - 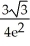
B) maximum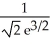 , minimum -
, minimum - 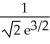
C) maximum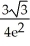 , minimum -
, minimum - 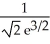
D) maximum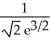 , minimum 0
, minimum 0
E) no extreme values exist
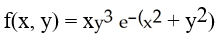 on the semi-infinite strip 0 ≤ x < ∞, -1 ≤ y ≤ 2, if these extreme values exist.
on the semi-infinite strip 0 ≤ x < ∞, -1 ≤ y ≤ 2, if these extreme values exist. A) maximum
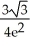 , minimum -
, minimum - 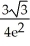
B) maximum
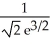 , minimum -
, minimum - 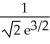
C) maximum
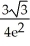 , minimum -
, minimum - 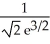
D) maximum
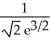 , minimum 0
, minimum 0E) no extreme values exist

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
26
Find the absolute maximum and absolute minimum values of f(x , y) = cos(x) + cos(y) - cos(x + y) - 1 on the closed square region bounded by the straight lines x = 0, y = 0, x = , and y = .
A) absolute minimum 0, absolute maximum
B) absolute minimum -4, absolute maximum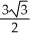 - 1
- 1
C) absolute minimum -4, absolute maximum
D) absolute minimum -2, absolute maximum 0
E) absolute minimum -4, no absolute maximum
A) absolute minimum 0, absolute maximum

B) absolute minimum -4, absolute maximum
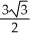 - 1
- 1C) absolute minimum -4, absolute maximum

D) absolute minimum -2, absolute maximum 0
E) absolute minimum -4, no absolute maximum

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
27
Use Lagrange multipliers to find the extreme values of f(x, y) = x2 + 3y2 + 2y on the unit circle x2 + y2 = 1.
A) maximum 6, minimum -
B) maximum 5, minimum -
C) maximum 6, minimum 0
D) maximum 5, minimum
E) maximum 5, minimum 1
A) maximum 6, minimum -

B) maximum 5, minimum -

C) maximum 6, minimum 0
D) maximum 5, minimum

E) maximum 5, minimum 1

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
28
Find the maximum and minimum values of f(x, y) = x2 + 3y2 + 2y on the disk x2 + y2 1. Use Lagrange multipliers to handle the boundary analysis.
A) maximum 6, minimum -
B) maximum 5, minimum -
C) maximum 6, minimum 0
D) maximum 5, minimum
E) maximum 5, minimum
A) maximum 6, minimum -

B) maximum 5, minimum -

C) maximum 6, minimum 0
D) maximum 5, minimum

E) maximum 5, minimum


Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
29
Find the maximum and minimum distances from the origin to the ellipse 5x2 + 6xy + 5y2 - 8 = 0.
A) maximum 2, minimum 1
B) maximum 4, minimum 1
C) maximum 2, minimum
D) maximum 4, minimum
E) maximum 4, minimum 2
A) maximum 2, minimum 1
B) maximum 4, minimum 1
C) maximum 2, minimum

D) maximum 4, minimum

E) maximum 4, minimum 2

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
30
Find the point on the sphere x2 + y2 + z2 = 10 that is closest to the point (1, -8, 5).
A)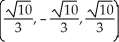
B)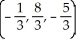
C) (0,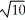 , 0)
, 0)
D)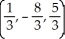
E) (2, -16, 10)
A)
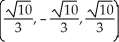
B)
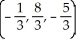
C) (0,
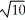 , 0)
, 0)D)
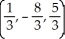
E) (2, -16, 10)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
31
Use Lagrange multipliers to find the maximum and minimum values of the functionf(x, y, z) = xy2z3 on the sphere x2 + y2 + z2 = 6.
A) maximum 6, minimum -6
B) maximum 6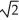 , minimum -6
, minimum -6 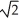
C) maximum 6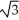 , minimum -6
, minimum -6 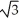
D) maximum 12, minimum -12
E) maximum 12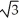 , minimum -12
, minimum -12 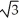
A) maximum 6, minimum -6
B) maximum 6
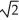 , minimum -6
, minimum -6 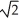
C) maximum 6
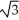 , minimum -6
, minimum -6 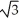
D) maximum 12, minimum -12
E) maximum 12
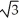 , minimum -12
, minimum -12 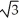

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
32
Find the point on the surface z = x2 + y2 closest to the point (1, 1, 0).
A) (1, 1, 1)
B)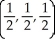
C)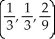
D)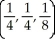
E)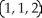
A) (1, 1, 1)
B)
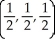
C)
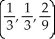
D)
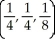
E)
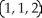

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
33
Find the maximum and minimum values of f(x , y) = x2 + xy + 2y2 subject to the constraint x2 + 3y2 = 3.
A) minimum 0 , maximum 3
B) minimum 2 , maximum 3
C) minimum , maximum
, maximum 
D) minimum 3 , maximum
E) minimum , maximum 2
, maximum 2
A) minimum 0 , maximum 3
B) minimum 2 , maximum 3
C) minimum
 , maximum
, maximum 
D) minimum 3 , maximum

E) minimum
 , maximum 2
, maximum 2
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
34
Use Lagrange multipliers to find the maximum and minimum values of the functionf(x, y) = x2y + z subject to the constraints x2 + y2 = 1 and z = y.
A) ±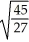
B) ±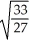
C) ±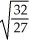
D) ±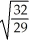
E) ±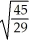
A) ±
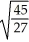
B) ±
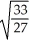
C) ±
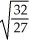
D) ±
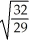
E) ±
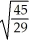

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
35
Let f(x, y, z) = x2 + 2y2 + 4z2. Find the point on the plane x + y + z = 14 at which f has its smallest value.
A) (8, 4, 2)
B) (0, 0, 14)
C) (1, 2, 11)
D)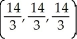
E) (2, 4, 8)
A) (8, 4, 2)
B) (0, 0, 14)
C) (1, 2, 11)
D)
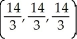
E) (2, 4, 8)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
36
Find the points closest to the origin on the hyperbola in which the cone x2 + y2 = z2 intersects the plane x + y = 2.
A) (1, 1, ±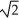 )
)
B) (-1, -1, ±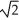 )
)
C) (-1, -1, ±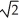 ) and (1, 1, ±
) and (1, 1, ± 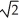 )
)
D) (2, 0, 2) and (0, 2, 2)
E) (1, 1,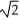 ) and (-1, -1, -
) and (-1, -1, - 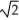 )
)
A) (1, 1, ±
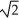 )
)B) (-1, -1, ±
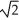 )
)C) (-1, -1, ±
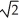 ) and (1, 1, ±
) and (1, 1, ± 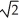 )
)D) (2, 0, 2) and (0, 2, 2)
E) (1, 1,
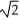 ) and (-1, -1, -
) and (-1, -1, - 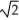 )
)
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
37
Find the maximum and minimum values of the function f(x, y, z) = 3x2 + 3y2 + 5 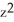 + 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.
+ 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.
A) maximum value 18, minimum value 12
B) maximum value 36, minimum value 12
C) maximum value 20, minimum value 18
D) maximum value 36, minimum value 18
E) maximum value 24, minimum value 16
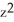 + 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.
+ 2xy - 2xz - 2yz over the sphere x2 + y2 + z2 = 6.A) maximum value 18, minimum value 12
B) maximum value 36, minimum value 12
C) maximum value 20, minimum value 18
D) maximum value 36, minimum value 18
E) maximum value 24, minimum value 16

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
38
If the Lagrange function L corresponding to the problem of extremizing f(x, y, z) subject to the constraint g(x, y, z) = 0 has exactly two critical points, then f must attain its maximum value at one of the points and attain its minimum value at the other point.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
39
The extreme values of the function f(x , y, z) = 23 x + y2z subject to the constraintsx - z = 0 and y2 + z2 = 36 are given by:
A) 115, 128
B) - 115, 115
C) -128, 115
D) -128, 128
E) -128, -115
A) 115, 128
B) - 115, 115
C) -128, 115
D) -128, 128
E) -128, -115

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
40
Find the maximum and minimum values of the function f(x, y, z, u, v) = x2 + y2 + z2 + u2 + v2 subject to the constraints x + y + 3z = 7 and 3z - u -v = 13.
A) maximum 19, occurs at the point (x, y, z, u, v) = (- 1, -1, 3, -2, -2) and no minimum value
B) minimum 19, occurs at the point (x, y, z, u, v) = (- 1,- 1, 3, -2, -2) and no maximum value
C) maximum 89, occurs at the point (x, y, z, u, v) = (1, 1, -9, 2, 2) and no minimum value
D) minimum 0, occurs at the point (x, y, z, u, v) = (0, 0, 0, 0, 0) and no maximum value
E) There are no finite extreme values.
A) maximum 19, occurs at the point (x, y, z, u, v) = (- 1, -1, 3, -2, -2) and no minimum value
B) minimum 19, occurs at the point (x, y, z, u, v) = (- 1,- 1, 3, -2, -2) and no maximum value
C) maximum 89, occurs at the point (x, y, z, u, v) = (1, 1, -9, 2, 2) and no minimum value
D) minimum 0, occurs at the point (x, y, z, u, v) = (0, 0, 0, 0, 0) and no maximum value
E) There are no finite extreme values.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
41
Let pi > 0, i = 1, 2, 3,..., n be real numbers such that 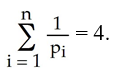
Find the maximum value of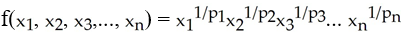 subject to the constraint
subject to the constraint 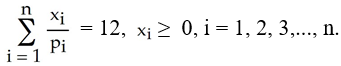
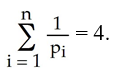
Find the maximum value of
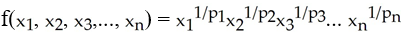 subject to the constraint
subject to the constraint 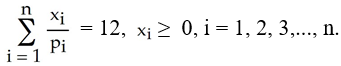

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
42
Use Lagrange multipliers to find the point P( 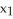 ,
, 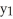 ,
, 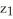 ) on the sphere
) on the sphere 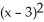 +
+ 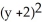 +
+ 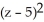 = 9 and the point Q (
= 9 and the point Q ( 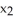 ,
, 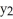 ,
, 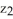 ) on the plane x + 2y - 2z = 7 where the distance between P and Q is minimum and determine this minimum distance.
) on the plane x + 2y - 2z = 7 where the distance between P and Q is minimum and determine this minimum distance.
A) P (2, -4, 7), Q (5, 2, 1); minimum distance 9 units
B) P (4, 0, 3), Q (3, -2, 5); minimum distance 3 units
C) P (4, 0, 3), Q (5, 2, 1); minimum distance 3 units
D) P (2, -4, 7), Q (-1, -10, 13); minimum distance 9 units
E) P (2, -4, 7), Q (1, -6, 9); minimum distance 3 units
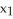 ,
, 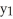 ,
, 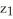 ) on the sphere
) on the sphere 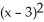 +
+ 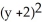 +
+ 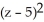 = 9 and the point Q (
= 9 and the point Q ( 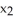 ,
, 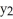 ,
, 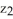 ) on the plane x + 2y - 2z = 7 where the distance between P and Q is minimum and determine this minimum distance.
) on the plane x + 2y - 2z = 7 where the distance between P and Q is minimum and determine this minimum distance.A) P (2, -4, 7), Q (5, 2, 1); minimum distance 9 units
B) P (4, 0, 3), Q (3, -2, 5); minimum distance 3 units
C) P (4, 0, 3), Q (5, 2, 1); minimum distance 3 units
D) P (2, -4, 7), Q (-1, -10, 13); minimum distance 9 units
E) P (2, -4, 7), Q (1, -6, 9); minimum distance 3 units

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
43
Find and classify the critical points of the Lagrange function L( 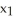 ,
, 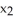 ,...,
,..., 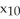 , λ) corresponding to the problem:extremize
, λ) corresponding to the problem:extremize 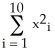 subject to =
subject to = 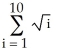 .
. 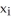
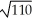
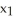 ,
, 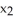 ,...,
,..., 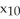 , λ) corresponding to the problem:extremize
, λ) corresponding to the problem:extremize 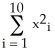 subject to =
subject to = 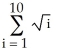 .
. 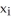
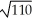

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
44
(i) Maximize 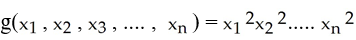 subject to the constraint x12 +x22 + ..... xn2 = 1.
subject to the constraint x12 +x22 + ..... xn2 = 1.
(ii) Use part (i) to prove the well-known Arithmetic-Geometric Inequality :
For any positive real numbers y1 , y2 , ....... yn ,
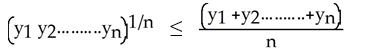
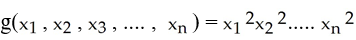 subject to the constraint x12 +x22 + ..... xn2 = 1.
subject to the constraint x12 +x22 + ..... xn2 = 1. (ii) Use part (i) to prove the well-known Arithmetic-Geometric Inequality :
For any positive real numbers y1 , y2 , ....... yn ,
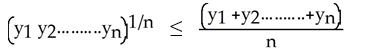

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
45
Starfleet Command has given Captain Kirk a subspace amplifier to channel communications among n star systems having galactic Cartesian coordinates ( 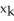 ,
, 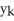 ,
, 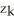 ) for k = 1, 2,..., n. To what point in space should Captain Kirk take the Enterprise to place the amplifier so as to minimize the sum of the squares of its distances from the n star systems?
) for k = 1, 2,..., n. To what point in space should Captain Kirk take the Enterprise to place the amplifier so as to minimize the sum of the squares of its distances from the n star systems?
A) the point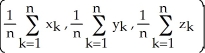
B) the point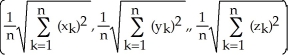
C) the point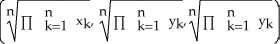
D) the point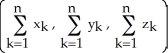
E) the point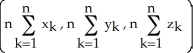
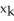 ,
, 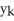 ,
, 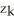 ) for k = 1, 2,..., n. To what point in space should Captain Kirk take the Enterprise to place the amplifier so as to minimize the sum of the squares of its distances from the n star systems?
) for k = 1, 2,..., n. To what point in space should Captain Kirk take the Enterprise to place the amplifier so as to minimize the sum of the squares of its distances from the n star systems?A) the point
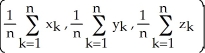
B) the point
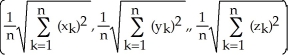
C) the point
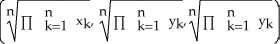
D) the point
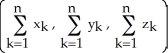
E) the point
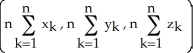

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
46
Find an equation of the line of best fit given the following points: (1, -1), (2, 1), (3, 2), (4, 1), and (5, 0).
A) y =
B) y = 5x
C) y = 2x -1
D) y = + 1
+ 1
E) y = - 1
- 1
A) y =

B) y = 5x
C) y = 2x -1
D) y =
 + 1
+ 1E) y =
 - 1
- 1
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
47
Find the value of the constant m so that the line y = mx best fits the experimental data (1, 2.3), (2, 4.2), (3, 7.1), (4, 8.8) in the sense of minimizing the sum of the squares of the vertical distances of the data points from the line.
A) m = 2.36
B) m = 2.24
C) m = 2.18
D) m = 2.11
E) m = 2.34
A) m = 2.36
B) m = 2.24
C) m = 2.18
D) m = 2.11
E) m = 2.34

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
48
Find the value of the constant a so that the graph of the function f(x) = ax2 best fits the curve y = ![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917d_a0f8_133208b18574_TB9661_11.jpg) on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.
on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.
A) a =![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917e_a0f8_074d4ee24ca4_TB9661_11.jpg)
B) a =![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917f_a0f8_d5105779fde5_TB9661_11.jpg)
C) a =![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9180_a0f8_9bad26bbb13e_TB9661_11.jpg)
D) a =![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9181_a0f8_358b147d4560_TB9661_11.jpg)
E) a =![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9182_a0f8_a51bd4ab3c61_TB9661_11.jpg)
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917d_a0f8_133208b18574_TB9661_11.jpg) on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.
on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.A) a =
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917e_a0f8_074d4ee24ca4_TB9661_11.jpg)
B) a =
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_917f_a0f8_d5105779fde5_TB9661_11.jpg)
C) a =
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9180_a0f8_9bad26bbb13e_TB9661_11.jpg)
D) a =
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9181_a0f8_358b147d4560_TB9661_11.jpg)
E) a =
![<strong>Find the value of the constant a so that the graph of the function f(x) = ax<sup>2</sup> best fits the curve y = on the interval [0, 1] in the sense of minimizing the integral of the square of the vertical distance between the two curves on that interval.</strong> A) a = B) a = C) a = D) a = E) a =](https://storage.examlex.com/TB9661/11ee77e1_77ae_9182_a0f8_a51bd4ab3c61_TB9661_11.jpg)

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
49
Find the empirical regression line y = a + bx for the data (x , y) = (1, -2), 4, 1), and (1, 10). What is the predicted value of y when x = -3?

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
50
Find the values of constant real numbers a and b to minimize 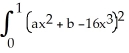 dx.
dx.
A) a = 15 , b = -1
B) a = 19 , b = -
C) a = - 24 , b = 4
D) a = - , b =
, b = 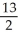
E) a = 24 , b = - 4
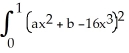 dx.
dx.A) a = 15 , b = -1
B) a = 19 , b = -

C) a = - 24 , b = 4
D) a = -
 , b =
, b = 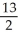
E) a = 24 , b = - 4

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
51
Find the derivative of the function f(x) = 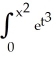 dt.
dt.
A) 6x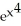
B) 4x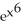
C) 2x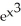
D) 2x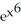
E) 2x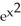
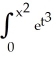 dt.
dt.A) 6x
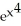
B) 4x
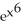
C) 2x
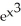
D) 2x
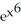
E) 2x
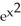

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
52
Use the fact that 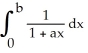 =
=  ln (1 + ab) to evaluate
ln (1 + ab) to evaluate 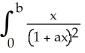 dx.
dx.
A)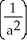 ln (1 + ab) +
ln (1 + ab) + 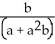
B)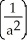 ln (1 + ab) +
ln (1 + ab) + 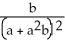
C)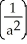 ln (1 + ab) -
ln (1 + ab) - 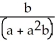
D)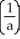 ln (1 + ab) -
ln (1 + ab) - 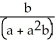
E)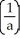 ln (1 + ab) +
ln (1 + ab) + 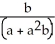
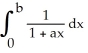 =
=  ln (1 + ab) to evaluate
ln (1 + ab) to evaluate 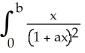 dx.
dx.A)
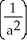 ln (1 + ab) +
ln (1 + ab) + 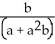
B)
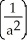 ln (1 + ab) +
ln (1 + ab) + 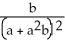
C)
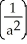 ln (1 + ab) -
ln (1 + ab) - 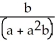
D)
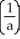 ln (1 + ab) -
ln (1 + ab) - 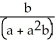
E)
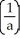 ln (1 + ab) +
ln (1 + ab) + 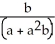

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
53
By first differentiating the integral, evaluate 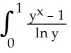 dy for x > -1.
dy for x > -1.
A) ln (2x + 1)
B) ln (|x|) + 1
C) ln (x - 1)
D) ln (x + 1)
E) ln (x) + 1
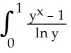 dy for x > -1.
dy for x > -1.A) ln (2x + 1)
B) ln (|x|) + 1
C) ln (x - 1)
D) ln (x + 1)
E) ln (x) + 1

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the integral equation f(x) = 3 + 2 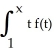 dt.
dt.
A) f(x) = 2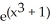
B) f(x) = 3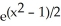
C) f(x) = 2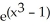
D) f(x) = 3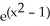
E) f(x) = 3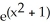
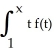 dt.
dt.A) f(x) = 2
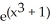
B) f(x) = 3
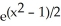
C) f(x) = 2
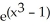
D) f(x) = 3
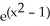
E) f(x) = 3
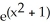

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
55
Find the envelope of the family of straight lines y - 3 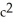 x + 2
x + 2 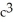 = 0.
= 0.
A) y = x3
B) y = 2x3
C) y2 = x3
D) y2 = 3x3
E) y = 3x3
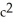 x + 2
x + 2 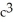 = 0.
= 0.A) y = x3
B) y = 2x3
C) y2 = x3
D) y2 = 3x3
E) y = 3x3

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
56
Given F(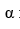 ) =
) = 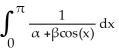 =
= 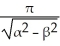 , for
, for 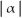 >
> 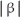 .
.
By first differentiating F with respect to 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11, evaluate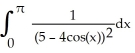 .
.
A)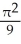
B)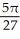
C) -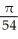
D)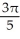
E)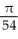
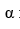 ) =
) = 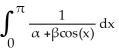 =
= 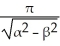 , for
, for 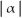 >
> 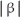 .
.By first differentiating F with respect to 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11, evaluate
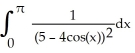 .
.A)
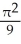
B)
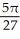
C) -
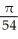
D)
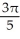
E)
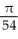

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate F(x,y) = 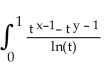 dt for x > 0, y > 0.
dt for x > 0, y > 0.
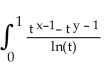 dt for x > 0, y > 0.
dt for x > 0, y > 0.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
58
Find the envelope of the family of straight lines xcosh(c) + ysinh(c) = 3.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
59
Every one-parameter family of curves in the plane has an envelope.

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
60
Use Newton's method to solve the system ( 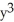 + y)
+ y) 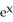 = 2,
= 2, 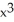 -
- 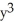 = 1.
= 1.
A) x = 1.0502656, y = 0.54118591
B) x = 1.0503479, y = 0.54110211
C) x = 1.0510302, y = 0.54116463
D) x = 1.0514452, y = 0.54230058
E) x = 1.0523415, y = 0.54435746
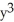 + y)
+ y) 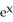 = 2,
= 2, 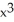 -
- 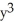 = 1.
= 1.A) x = 1.0502656, y = 0.54118591
B) x = 1.0503479, y = 0.54110211
C) x = 1.0510302, y = 0.54116463
D) x = 1.0514452, y = 0.54230058
E) x = 1.0523415, y = 0.54435746

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
61
Use Newton's method to find a first quadrant solution of the system x2 + y4 = 1, y3 = 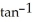 (
( 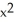 ).
).
A) x = 0.40784120, y = 0.96737370
B) x = 0.88321233, y = 0.76223749
C) x = 0.72413552, y = 0.74316200
D) x = 0.76006565, y = 0.80613044
E) x = 0.64874536, y = 0.64385647
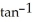 (
( 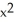 ).
).A) x = 0.40784120, y = 0.96737370
B) x = 0.88321233, y = 0.76223749
C) x = 0.72413552, y = 0.74316200
D) x = 0.76006565, y = 0.80613044
E) x = 0.64874536, y = 0.64385647

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
62
Use Maple's fsolve with Digits : = 6 to find a solution to the system 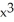 +
+ 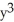 = 3, x sin(x) - y cos(y) = 0 near (1, 2).
= 3, x sin(x) - y cos(y) = 0 near (1, 2).
A) x = 0.461289, y = 1.42635
B) x = 0.462289, y = 1.53635
C) x = 0.465489, y = 1.48635
D) x = 0.460089, y = 1.42335
E) x = 0.463445, y = 1.41657
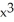 +
+ 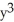 = 3, x sin(x) - y cos(y) = 0 near (1, 2).
= 3, x sin(x) - y cos(y) = 0 near (1, 2).A) x = 0.461289, y = 1.42635
B) x = 0.462289, y = 1.53635
C) x = 0.465489, y = 1.48635
D) x = 0.460089, y = 1.42335
E) x = 0.463445, y = 1.41657

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
63
Find and classify the critical points of f(x, y) = (2 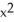 - xy + 5
- xy + 5 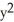 - x + 2y)
- x + 2y) 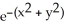 .
.
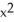 - xy + 5
- xy + 5 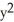 - x + 2y)
- x + 2y) 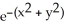 .
.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
64
Find the maximum and minimum values of the function f(x, y) = 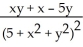 .
.
A) maximum 0.145490, minimum - 0.158939
B) maximum 0.146110, minimum - 0.160236
C) maximum 0.141191, minimum - 0.152573
D) maximum 0.129903, minimum - 0.173412
E) maximum 0.145276, minimum - 0.168873
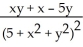 .
.A) maximum 0.145490, minimum - 0.158939
B) maximum 0.146110, minimum - 0.160236
C) maximum 0.141191, minimum - 0.152573
D) maximum 0.129903, minimum - 0.173412
E) maximum 0.145276, minimum - 0.168873

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
65
Find the minimum value of the function f(x, y) = x4 + y4 - xy + xy2
A) -0.382006
B) -0.362705
C) -0.077091
D) -0.051392
E) -0.243454
A) -0.382006
B) -0.362705
C) -0.077091
D) -0.051392
E) -0.243454

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
66
Use Maple's fsolve routine to solve the non-linear system of equations 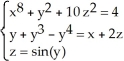 Quote the solution to 5 significant figures.
Quote the solution to 5 significant figures.
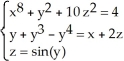 Quote the solution to 5 significant figures.
Quote the solution to 5 significant figures.
Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck
67
Find an optimal binary compression for a 16-character alphabet with probabilities given in the table below. Use four figures of accuracy. 
A) 3.0139
B) 0.8398
C) 0.5821
D) 0.2528
E) 0.3607

A) 3.0139
B) 0.8398
C) 0.5821
D) 0.2528
E) 0.3607

Unlock Deck
Unlock for access to all 67 flashcards in this deck.
Unlock Deck
k this deck


