Deck 9: Conics, Parametric Curves, and Polar Curves
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/114
Play
Full screen (f)
Deck 9: Conics, Parametric Curves, and Polar Curves
1
Find the equation of the parabola passing through the point (2, 5), having vertex at the origin and axis of symmetry along the y-axis.
A) 5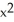 = y
= y
B) 5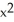 = 4y
= 4y
C) 4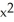 = 5y
= 5y
D) 3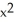 = 4y
= 4y
E)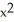 = 3y
= 3y
A) 5
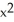 = y
= yB) 5
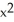 = 4y
= 4yC) 4
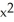 = 5y
= 5yD) 3
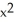 = 4y
= 4yE)
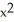 = 3y
= 3y5 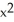 = 4y
= 4y
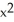 = 4y
= 4y 2
For the parabola 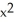 + 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.
+ 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.
A) Vertex (3, 1), Focus (3, 2), Directrix y = 0
B) Vertex (3, 1), Focus (3, 0), Directrix y = 2
C) Vertex (-3, 1), Focus (-3, 2), Directrix y = 0
D) Vertex (-3, 1), Focus (-3, 0), Directrix y = 2
E) Vertex (-3, -1), Focus (-3, 0), Directrix y = 2
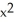 + 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.
+ 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.A) Vertex (3, 1), Focus (3, 2), Directrix y = 0
B) Vertex (3, 1), Focus (3, 0), Directrix y = 2
C) Vertex (-3, 1), Focus (-3, 2), Directrix y = 0
D) Vertex (-3, 1), Focus (-3, 0), Directrix y = 2
E) Vertex (-3, -1), Focus (-3, 0), Directrix y = 2
Vertex (-3, 1), Focus (-3, 0), Directrix y = 2
3
Find an equation of an ellipse satisfying the given conditions: Foci (-3, 0) and (3, 0) and length of major axis 6.
A)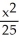 +
+ 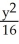 = 1
= 1
B)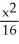 +
+ 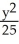 = 1
= 1
C)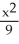 +
+ 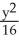 = 1
= 1
D)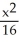 +
+ 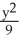 = 1
= 1
E)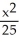 +
+ 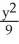 = 1
= 1
A)
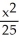 +
+ 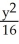 = 1
= 1B)
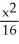 +
+ 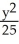 = 1
= 1C)
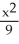 +
+ 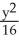 = 1
= 1D)
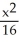 +
+ 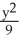 = 1
= 1E)
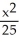 +
+ 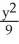 = 1
= 1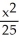 +
+ 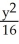 = 1
= 1 4
Find an equation of a parabola satisfying the given conditions Focus (4, 1) and directrixx = -2.
A)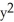 = 12x
= 12x
B)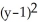 = 12(x - 1)
= 12(x - 1)
C)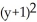 = 12(x + 1)
= 12(x + 1)
D)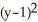 = -12(x - 1)
= -12(x - 1)
E)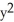 = 12x + 1
= 12x + 1
A)
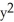 = 12x
= 12xB)
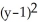 = 12(x - 1)
= 12(x - 1)C)
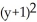 = 12(x + 1)
= 12(x + 1)D)
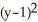 = -12(x - 1)
= -12(x - 1)E)
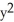 = 12x + 1
= 12x + 1
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
5
Find an equation of a parabola satisfying the given conditions: Focus (2, 0) and directrix y = 2?.
A)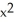 = 4 (1 - y)
= 4 (1 - y)
B)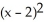 = 4( - y)
= 4( - y)
C)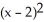 = 4 ( - y)
= 4 ( - y)
D)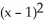 = 4 ( - y)
= 4 ( - y)
E)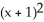 = 4 ( - y)
= 4 ( - y)
A)
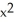 = 4 (1 - y)
= 4 (1 - y)B)
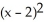 = 4( - y)
= 4( - y)C)
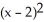 = 4 ( - y)
= 4 ( - y)D)
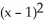 = 4 ( - y)
= 4 ( - y)E)
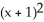 = 4 ( - y)
= 4 ( - y)
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
6
Find the centre, eccentricity, and foci of the ellipse 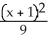 +
+ 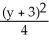 = 1.
= 1.
A) Centre (1, -3);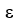 =
= 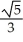 ; foci (1 ±
; foci (1 ± 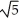 , -3)
, -3)
B) Centre (-1, 3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =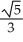 ; foci (-1 ±
; foci (-1 ± 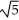 , 3)
, 3)
C) Centre (1, 3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =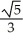 ; foci (1 ±
; foci (1 ± 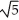 , 3)
, 3)
D) Centre (-1, -3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =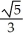 ; foci (-1 ±
; foci (-1 ± 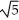 , -3)
, -3)
E) Centre (1, -3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =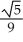 ; foci (1 ±
; foci (1 ± 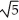 , -3)
, -3)
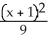 +
+ 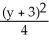 = 1.
= 1.A) Centre (1, -3);
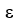 =
= 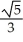 ; foci (1 ±
; foci (1 ± 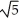 , -3)
, -3)B) Centre (-1, 3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =
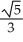 ; foci (-1 ±
; foci (-1 ± 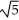 , 3)
, 3)C) Centre (1, 3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =
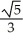 ; foci (1 ±
; foci (1 ± 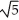 , 3)
, 3)D) Centre (-1, -3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =
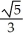 ; foci (-1 ±
; foci (-1 ± 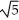 , -3)
, -3)E) Centre (1, -3); 11ee7b11_3aa8_6932_ae82_3b68ee6209d9_TB9661_11 =
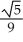 ; foci (1 ±
; foci (1 ± 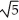 , -3)
, -3)
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
7
Find all values of the constant real number k so that the second degree equation 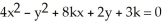 represents a pair of lines.
represents a pair of lines.
A) k = -1, k =
B) k = 1, -
C) k = - ,
, 
D) - < k <
E) k 0
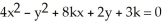 represents a pair of lines.
represents a pair of lines.A) k = -1, k =

B) k = 1, -

C) k = -
 ,
, 
D) - < k <
E) k 0

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
8
Find an equation of an ellipse containing the point (-  ,
, 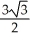 ) and with vertices (0, -3) and (0, 3).
) and with vertices (0, -3) and (0, 3).
A)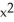 +
+ 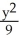 = 1
= 1
B)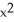 -
- 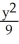 = 1
= 1
C)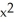 +
+ 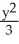 = 1
= 1
D)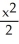 +
+ 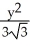 = 1
= 1
E)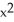 +
+ 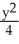 = 1
= 1
 ,
, 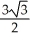 ) and with vertices (0, -3) and (0, 3).
) and with vertices (0, -3) and (0, 3).A)
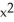 +
+ 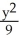 = 1
= 1B)
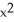 -
- 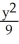 = 1
= 1C)
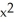 +
+ 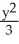 = 1
= 1D)
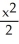 +
+ 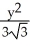 = 1
= 1E)
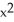 +
+ 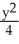 = 1
= 1
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
9
For the hyperbola 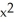 -
- 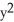 = 8x - 2y - 13, find the centre, the vertices, the foci, and the asymptotes.
= 8x - 2y - 13, find the centre, the vertices, the foci, and the asymptotes.
A) Centre (4, 1), Vertices (4 ±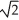 , 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
, 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
B) Centre (-4, -1), Vertices (-4 ±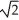 , -1), Foci (-4 ± 2, -1), Asymptotes x - y = -3 and x + y = -5
, -1), Foci (-4 ± 2, -1), Asymptotes x - y = -3 and x + y = -5
C) Centre (4, 1), Vertices (4 ±2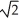 , 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
, 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
D) Centre (-4, 1), Vertices (-4 ±2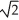 , 1), Foci (-4 ± 2, 1), Asymptotes x - y = -3 and x + y = 5
, 1), Foci (-4 ± 2, 1), Asymptotes x - y = -3 and x + y = 5
E) Centre (4, -1), Vertices (4 ±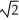 , -1), Foci (4 ± 2, -1), Asymptotes x + y = 3 and x - y = 5
, -1), Foci (4 ± 2, -1), Asymptotes x + y = 3 and x - y = 5
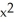 -
- 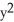 = 8x - 2y - 13, find the centre, the vertices, the foci, and the asymptotes.
= 8x - 2y - 13, find the centre, the vertices, the foci, and the asymptotes.A) Centre (4, 1), Vertices (4 ±
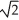 , 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
, 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5B) Centre (-4, -1), Vertices (-4 ±
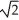 , -1), Foci (-4 ± 2, -1), Asymptotes x - y = -3 and x + y = -5
, -1), Foci (-4 ± 2, -1), Asymptotes x - y = -3 and x + y = -5C) Centre (4, 1), Vertices (4 ±2
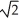 , 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5
, 1), Foci (4 ± 2, 1), Asymptotes x - y = 3 and x + y = 5D) Centre (-4, 1), Vertices (-4 ±2
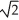 , 1), Foci (-4 ± 2, 1), Asymptotes x - y = -3 and x + y = 5
, 1), Foci (-4 ± 2, 1), Asymptotes x - y = -3 and x + y = 5E) Centre (4, -1), Vertices (4 ±
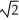 , -1), Foci (4 ± 2, -1), Asymptotes x + y = 3 and x - y = 5
, -1), Foci (4 ± 2, -1), Asymptotes x + y = 3 and x - y = 5
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
10
The maximum distance of the Earth from the sun is 9.3 × 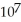 kilometres. The minimum distance is
kilometres. The minimum distance is 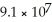 kilometres. The sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.
kilometres. The sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.
A) 3.2 × 106 kilometres
B) 4.8 × 106 kilometres
C) 6.4 × 106 kilometres
D) 1.6 × 106 kilometres
E) 8.0 × 106 kilometres
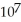 kilometres. The minimum distance is
kilometres. The minimum distance is 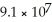 kilometres. The sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.
kilometres. The sun is at one focus of the elliptical orbit. Find the distance from the sun to the other focus.A) 3.2 × 106 kilometres
B) 4.8 × 106 kilometres
C) 6.4 × 106 kilometres
D) 1.6 × 106 kilometres
E) 8.0 × 106 kilometres

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
11
To eliminate the xy-term from the general equation of a conic section, 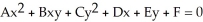 ,
, 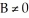 , we rotate the coordinate axes about the origin through an
, we rotate the coordinate axes about the origin through an 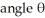 , where cot(2 ) =
, where cot(2 ) = 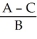 .
.
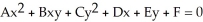 ,
, 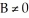 , we rotate the coordinate axes about the origin through an
, we rotate the coordinate axes about the origin through an 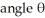 , where cot(2 ) =
, where cot(2 ) = 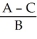 .
. 
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
12
Find the centre, the foci, and the asymptotes of the hyperbola 4 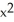 - 9
- 9 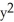 -16x - 54y = 101.
-16x - 54y = 101.
A) Centre (2, -3), Foci (2 ±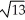 , -3), Asymptotes
, -3), Asymptotes 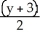 = ±
= ± 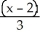
B) Centre (-2, 3), Foci (-2 ±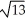 , 3), Asymptotes
, 3), Asymptotes 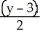 = ±
= ± 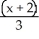
C) Centre (2, -3), Foci (2 ±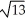 , -3), Asymptotes
, -3), Asymptotes 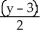 = ±
= ± 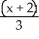
D) Centre (2, 3), Foci (2 ±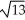 , 3), Asymptotes
, 3), Asymptotes 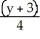 = ±
= ± 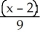
E) Centre (-2, 3), Foci (-2 ±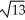 , 3), Asymptotes
, 3), Asymptotes 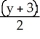 = ±
= ± 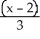
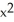 - 9
- 9 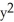 -16x - 54y = 101.
-16x - 54y = 101.A) Centre (2, -3), Foci (2 ±
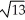 , -3), Asymptotes
, -3), Asymptotes 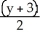 = ±
= ± 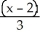
B) Centre (-2, 3), Foci (-2 ±
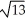 , 3), Asymptotes
, 3), Asymptotes 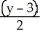 = ±
= ± 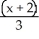
C) Centre (2, -3), Foci (2 ±
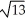 , -3), Asymptotes
, -3), Asymptotes 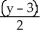 = ±
= ± 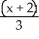
D) Centre (2, 3), Foci (2 ±
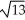 , 3), Asymptotes
, 3), Asymptotes 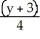 = ±
= ± 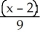
E) Centre (-2, 3), Foci (-2 ±
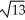 , 3), Asymptotes
, 3), Asymptotes 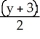 = ±
= ± 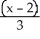

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
13
Find an equation of a hyperbola with vertices (3, 7) and (-3, 7) and 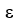 =
=  .
.
A)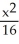 -
- 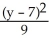 = 1
= 1
B)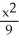 -
- 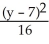 = 1
= 1
C)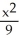 -
- 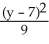 = 1
= 1
D)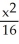 -
- 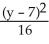 = 1
= 1
E)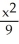 -
- 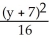 = 1
= 1
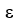 =
=  .
.A)
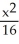 -
- 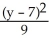 = 1
= 1B)
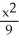 -
- 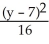 = 1
= 1C)
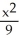 -
- 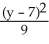 = 1
= 1D)
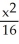 -
- 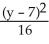 = 1
= 1E)
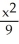 -
- 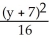 = 1
= 1
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
14
Find an equation of a hyperbola with vertices (-1, 3) and (-1, 7) and  = 4.
= 4.
A)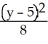 -
- 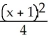 = 1
= 1
B)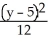 -
- 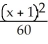 = 1
= 1
C)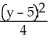 -
- 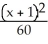 = 1
= 1
D)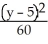 -
- 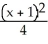 = 1
= 1
E)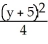 -
- 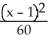 = 1
= 1
 = 4.
= 4.A)
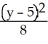 -
- 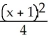 = 1
= 1B)
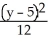 -
- 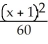 = 1
= 1C)
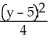 -
- 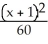 = 1
= 1D)
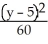 -
- 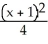 = 1
= 1E)
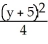 -
- 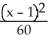 = 1
= 1
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
15
Find the angle at which the parabolas y2 = 4x + 4 and y2 = -6x + 9 intersect at each of their intersection points.
A) 90º at each intersection point
B) 120º at each intersection point
C) 60º at each intersection point
D) 75º at each intersection point
E) 50º at each intersection point
A) 90º at each intersection point
B) 120º at each intersection point
C) 60º at each intersection point
D) 75º at each intersection point
E) 50º at each intersection point

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
16
Find the points on the hyperbola x2 - y2 = 1 nearest to the point (0, 1).
A)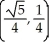 ,
, 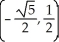
B)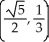 ,
, 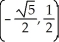
C)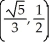 ,
, 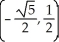
D)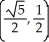 ,
, 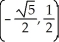
E)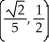 ,
, 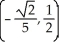
A)
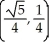 ,
, 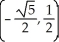
B)
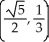 ,
, 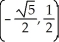
C)
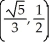 ,
, 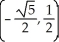
D)
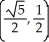 ,
, 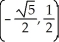
E)
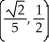 ,
, 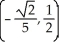

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
17
A circle passes through both foci of an ellipse and is tangent to the ellipse at two points. Find the eccentricity of the ellipse.
A)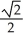
B)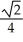
C)
D)
E)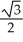
A)
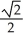
B)
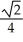
C)

D)

E)
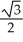

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
18
A conic section is given by the equation 4x2 + 10xy + 4y2 = 36.Use rotation of coordinate axes through an appropriate acute angle to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( ) - v sin( ) , y = u sin( ) + v cos( ). Then identify the conic section.
A)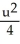 +
+ 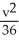 = 1, an ellipse
= 1, an ellipse
B)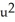 +
+ 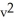 = 4, a circle
= 4, a circle
C)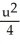 -
- 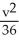 = 1, a hyperbola
= 1, a hyperbola
D)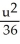 +
+ 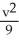 = 1, an ellipse
= 1, an ellipse
E)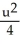 -
- 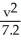 = 1, a hyperbola
= 1, a hyperbola
A)
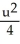 +
+ 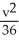 = 1, an ellipse
= 1, an ellipseB)
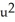 +
+ 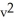 = 4, a circle
= 4, a circleC)
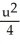 -
- 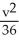 = 1, a hyperbola
= 1, a hyperbolaD)
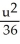 +
+ 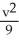 = 1, an ellipse
= 1, an ellipseE)
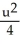 -
- 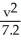 = 1, a hyperbola
= 1, a hyperbola
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
19
Find the equation to the ellipse for which (1, -1) is a focus, x - y = 3 is the corresponding directrix, and the eccentricity is 1/2.
A) 3x2 - 2xy + 3y2 - 2x + 2y - 1 = 0
B) 3x2 + 2xy + 3y2 - 2x + 2y - 1 = 0
C) 7x2 - 2xy + 7y2 - 10x + 10y + 7 = 0
D) 7x2 + 2xy + 7y2 - 10x + 10y + 7 = 0
E) 7x2 + 2xy + 7y2 - 5x + 5y - 2 = 0
A) 3x2 - 2xy + 3y2 - 2x + 2y - 1 = 0
B) 3x2 + 2xy + 3y2 - 2x + 2y - 1 = 0
C) 7x2 - 2xy + 7y2 - 10x + 10y + 7 = 0
D) 7x2 + 2xy + 7y2 - 10x + 10y + 7 = 0
E) 7x2 + 2xy + 7y2 - 5x + 5y - 2 = 0

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
20
Find the equation of the parabola whose focus is (2, -1) and directrix is x + 2y -1 = 0.
A) 4x2 - 4xy + y2 -18x + 14y + 24 = 0
B) 5x2 - 4xy + y2 -18x + 14y + 24 = 0
C) x2 - 4xy + 4y2 -18x + 14y + 24 = 0
D) x2 - 4xy + 5y2 -18x + 14y + 24 = 0
E) 4x2 - 4xy + 4y2 -18x + 14y + 24 = 0
A) 4x2 - 4xy + y2 -18x + 14y + 24 = 0
B) 5x2 - 4xy + y2 -18x + 14y + 24 = 0
C) x2 - 4xy + 4y2 -18x + 14y + 24 = 0
D) x2 - 4xy + 5y2 -18x + 14y + 24 = 0
E) 4x2 - 4xy + 4y2 -18x + 14y + 24 = 0

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following sets of parametric equations constitute a parametrization of the whole parabola y = x2?
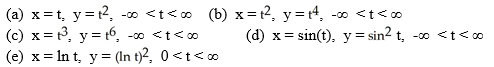
A) (a), (c), and (e) only
B) (a) and (e) only
C) (a), (b), and (c) only
D) all of them
E) none of them
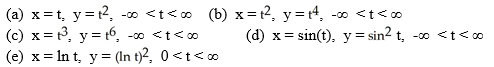
A) (a), (c), and (e) only
B) (a) and (e) only
C) (a), (b), and (c) only
D) all of them
E) none of them

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
22
What do the parametric equations x = 7 cos(t) and y = 3 sin(t) describe?
A) ellipse
B) hyperbola
C) circle
D) parabola
E) line
A) ellipse
B) hyperbola
C) circle
D) parabola
E) line

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
23
What do the parametric equations x = t2 + 3t and y = t + 4 describe?
A) parabola that opens to the right
B) parabola that opens to the left
C) ellipse
D) hyperbola
E) line
A) parabola that opens to the right
B) parabola that opens to the left
C) ellipse
D) hyperbola
E) line

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
24
A plane curve C is given parametrically by the functions x (t) = cosh(t) - 2, y(t) = sinh(t), t  R.
R.
A Cartesian equation of the curve C is given by:
A)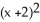 -
- 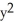 = 1
= 1
B)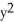 +
+ 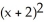 = 1
= 1
C)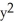 -
- 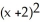 =1
=1
D)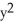 +
+ 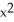 = 5
= 5
E)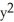 -
- 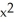 = 5
= 5
 R.
R.A Cartesian equation of the curve C is given by:
A)
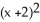 -
- 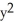 = 1
= 1B)
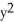 +
+ 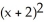 = 1
= 1C)
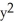 -
- 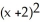 =1
=1D)
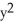 +
+ 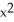 = 5
= 5E)
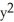 -
- 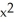 = 5
= 5
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
25
Find parametric equations of the plane curve C given by 4x2 + 9y2 - 8x -32 = 0.
A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t![<strong>Find parametric equations of the plane curve C given by 4x<sup>2</sup> + 9y<sup>2</sup> - 8x -32 = 0.</strong> A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] E)](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0 , 2 ]
[0 , 2 ]
B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
E)![<strong>Find parametric equations of the plane curve C given by 4x<sup>2</sup> + 9y<sup>2</sup> - 8x -32 = 0.</strong> A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] E)](https://storage.examlex.com/TB9661/11ee77e1_77d3_08d2_a0f8_2307eec9bd68_TB9661_11.jpg)
A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t
![<strong>Find parametric equations of the plane curve C given by 4x<sup>2</sup> + 9y<sup>2</sup> - 8x -32 = 0.</strong> A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] E)](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0 , 2 ]
[0 , 2 ]B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [0 , 2 ]
E)
![<strong>Find parametric equations of the plane curve C given by 4x<sup>2</sup> + 9y<sup>2</sup> - 8x -32 = 0.</strong> A) x(t) = 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] B) x(t) = - 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] C) x(t) = - 1 + 2cos(t), y(t) = 3sin(t), t [0 , 2 \pi ] D) x(t) = 1 + 3cos(t), y(t) = 2sin(t), t [0 , 2 \pi ] E)](https://storage.examlex.com/TB9661/11ee77e1_77d3_08d2_a0f8_2307eec9bd68_TB9661_11.jpg)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
26
Find the Cartesian coordinates of points of intersection of the plane parametric curves 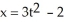 ,
, 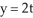 and x =
and x = 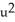 , y = -u - 1.
, y = -u - 1.
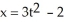 ,
, 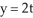 and x =
and x = 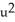 , y = -u - 1.
, y = -u - 1.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
27
A plane curve C is given parametrically by x = tan(t) - 2, y = sec(t), t  (-
(- 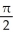 ,
, 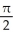 ).Find the Cartesian equation of the curve C.
).Find the Cartesian equation of the curve C.
A)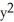 -
- 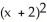 = 1, y 1
= 1, y 1
B)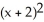 -
- 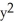 = 1, y 1
= 1, y 1
C)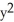 +
+ 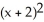 = 1, - < y <
= 1, - < y <
D)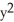 -
- 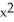 = 5, -1 y 1
= 5, -1 y 1
E)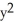 -
- 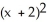 = 1, y - 1
= 1, y - 1
 (-
(- 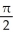 ,
, 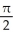 ).Find the Cartesian equation of the curve C.
).Find the Cartesian equation of the curve C.A)
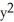 -
- 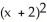 = 1, y 1
= 1, y 1B)
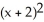 -
- 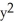 = 1, y 1
= 1, y 1C)
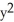 +
+ 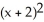 = 1, - < y <
= 1, - < y < D)
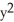 -
- 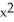 = 5, -1 y 1
= 5, -1 y 1E)
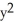 -
- 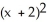 = 1, y - 1
= 1, y - 1
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
28
The equations x(t) = 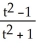 , y(t) =
, y(t) = 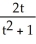 , -1 t 1 are the parametric equations of
, -1 t 1 are the parametric equations of
A) the whole circle centred at (0 , 0) and is of radius 1 unit
B) the left half of the circle centred at (0 , 0) and is of radius 1 unit
C) the bottom half of the circle centred at (0 , 0) and is of radius 1 unit
D) the top half of the circle centred at (0 , 0) and is of radius 1 unit
E) the right half of the circle centred at (0 , 0) and is of radius 1 unit
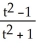 , y(t) =
, y(t) = 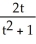 , -1 t 1 are the parametric equations of
, -1 t 1 are the parametric equations ofA) the whole circle centred at (0 , 0) and is of radius 1 unit
B) the left half of the circle centred at (0 , 0) and is of radius 1 unit
C) the bottom half of the circle centred at (0 , 0) and is of radius 1 unit
D) the top half of the circle centred at (0 , 0) and is of radius 1 unit
E) the right half of the circle centred at (0 , 0) and is of radius 1 unit

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
29
Describe the curve x = 3 - cos(t), y = -2 + 2 sin(t).
A) ellipse, centre (3, -2) with major axis along the line x = 3
B) ellipse, centre (3, -2) with major axis along the line y = -2
C) hyperbola, centre (3, -2) with transverse axis along the line x = -3
D) hyperbola, centre (3, -2) with transverse axis along the line x = 3
E) ellipse, centre (-3, 2) with major axis along the line x = -3
A) ellipse, centre (3, -2) with major axis along the line x = 3
B) ellipse, centre (3, -2) with major axis along the line y = -2
C) hyperbola, centre (3, -2) with transverse axis along the line x = -3
D) hyperbola, centre (3, -2) with transverse axis along the line x = 3
E) ellipse, centre (-3, 2) with major axis along the line x = -3

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
30
Parametrize the curve y = 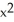 + 3x using its slope m as the parameter.
+ 3x using its slope m as the parameter.
A) x =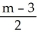 , y =
, y = 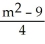
B) x =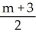 , y =
, y = 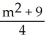
C) x =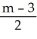 , y =
, y = 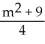
D) x =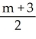 , y =
, y = 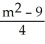
E) x =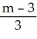 , y =
, y = 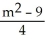
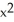 + 3x using its slope m as the parameter.
+ 3x using its slope m as the parameter.A) x =
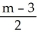 , y =
, y = 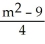
B) x =
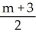 , y =
, y = 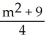
C) x =
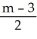 , y =
, y = 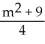
D) x =
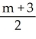 , y =
, y = 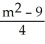
E) x =
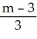 , y =
, y = 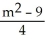

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following plane parametric curves is a parametrization of an ellipse centred at (4, -2)?
A) x = 3 - 4cos(t), y = 5 + 2sin(t), 0 t 2
B) x = 3 + 4cos(t), y = 5 - 2sin(t), 0 t 2
C) x = 4 + 3cos(t), y = -2 + 5sin(t), 0 t 2
D) x = - 4 + 3cos(t), y = 2 + 5sin(t), 0 t 2
E) x = 4 - 2cos(t), y = 4 - 2sin(t), 0 t 2
A) x = 3 - 4cos(t), y = 5 + 2sin(t), 0 t 2
B) x = 3 + 4cos(t), y = 5 - 2sin(t), 0 t 2
C) x = 4 + 3cos(t), y = -2 + 5sin(t), 0 t 2
D) x = - 4 + 3cos(t), y = 2 + 5sin(t), 0 t 2
E) x = 4 - 2cos(t), y = 4 - 2sin(t), 0 t 2

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
32
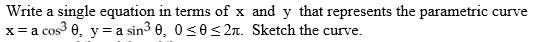

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
33
Find g(t) so that x = -1 + 3 cos(t), y = g(t), 0 t 2 provides a counterclockwise parametrization of the circle 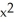 +
+ 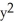 + 2x - 4y = 4.
+ 2x - 4y = 4.
A) -2 + sin(t)
B) 2 - 3 sin(t)
C) 2 + 3 sin(t)
D) 3 - 2 sin(t)
E) 3 + 2 sin(t)
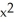 +
+ 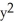 + 2x - 4y = 4.
+ 2x - 4y = 4.A) -2 + sin(t)
B) 2 - 3 sin(t)
C) 2 + 3 sin(t)
D) 3 - 2 sin(t)
E) 3 + 2 sin(t)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following best describes the parametric curve x = sec(t), y = 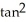 (t),-
(t),- 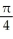 t
t 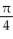 ?
?
A) part of the parabola y = x2 - 1 lying under the line y = 1
B) the parabola y = x2 - 1
C) part of the parabola y = x2 - 1 lying above the line y = 1
D) part of the parabola y = x2 - 1 lying above the line y = -1
E) part of the parabola y = x2 - 1 lying under the line y = 1 in the first quadrant
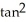 (t),-
(t),- 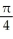 t
t 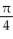 ?
?A) part of the parabola y = x2 - 1 lying under the line y = 1
B) the parabola y = x2 - 1
C) part of the parabola y = x2 - 1 lying above the line y = 1
D) part of the parabola y = x2 - 1 lying above the line y = -1
E) part of the parabola y = x2 - 1 lying under the line y = 1 in the first quadrant

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
35
Find the slope of the curve x = 6t + 3, y = 2 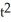 - 7t when t = 5.
- 7t when t = 5.
A) 6
B) 3
C)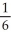
D)
E) 0
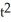 - 7t when t = 5.
- 7t when t = 5.A) 6
B) 3
C)
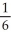
D)

E) 0

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
36
Find the equation of the tangent line to the curve at the given t.
X = cos 3t, y = 3 sin 5t at t =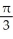 .
.
A) x + y = 2
B) y = -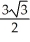
C) x = -1
D) x + y + 1 +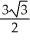 = 0
= 0
E) x = 1
X = cos 3t, y = 3 sin 5t at t =
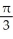 .
.A) x + y = 2
B) y = -
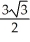
C) x = -1
D) x + y + 1 +
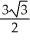 = 0
= 0E) x = 1

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
37
Find the equation of the tangent line to the curve at the given t. x = 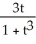 , y =
, y = 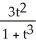 at t = 1.
at t = 1.
A) x + y = 3
B) 2x + y = 5
C) 2x - y = 3
D) x - y = 1
E) x + 2y = 3
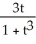 , y =
, y = 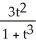 at t = 1.
at t = 1.A) x + y = 3
B) 2x + y = 5
C) 2x - y = 3
D) x - y = 1
E) x + 2y = 3

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
38
Find the slope of the curve x = 5 cos t, y = 3 sin t at t = 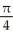 .
.
A)
B) -
C) -
D)
E) 1
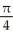 .
.A)

B) -

C) -

D)

E) 1

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
39
Find the equation of the tangent line to the curve at the given t. x = 2 cot t, y = 2 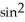 t at t =
t at t = 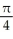
A) x - 2y = 0
B) x + 2y = 4
C) 2x + y = 5
D) 2x - y = 3
E) x - 2y = 4
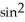 t at t =
t at t = 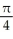
A) x - 2y = 0
B) x + 2y = 4
C) 2x + y = 5
D) 2x - y = 3
E) x - 2y = 4

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
40
Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by 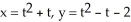 at the point on the curve where t = -1.
at the point on the curve where t = -1.
A) x + y = 0
B) 3x - y =0
C) y = 0
D) y = x
x
E) y = -3x
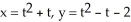 at the point on the curve where t = -1.
at the point on the curve where t = -1.A) x + y = 0
B) 3x - y =0
C) y = 0
D) y =
 x
xE) y = -3x

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
41
Express 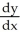 and
and 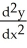 in terms of x and y for the circle x = a cos
in terms of x and y for the circle x = a cos
, y = a sin
.
A)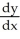 = -
= -  ,
, 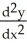 = -
= - 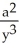
B)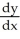 =
=  ,
, 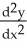 =
= 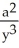
C) = -
= -  ,
, 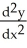 = -
= - 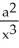
D)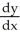 =
=  ,
, 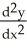 = -
= - 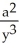
E)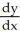 =
=  ,
, 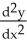 = -
= - 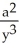
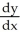 and
and 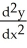 in terms of x and y for the circle x = a cos
in terms of x and y for the circle x = a cos , y = a sin
.
A)
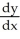 = -
= -  ,
, 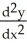 = -
= - 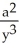
B)
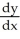 =
=  ,
, 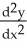 =
= 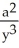
C)
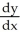 = -
= -  ,
, 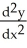 = -
= - 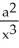
D)
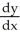 =
=  ,
, 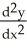 = -
= - 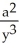
E)
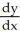 =
=  ,
, 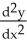 = -
= - 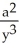

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
42
Determine the points where the parametric curve x = 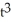 - 3t, y =
- 3t, y = 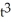 - 12t have horizontal and vertical tangents.
- 12t have horizontal and vertical tangents.
A) horizontal tangents at (2, 11), (-2, -11) and vertical tangents at (2, -16), (-2, 16)
B) horizontal tangent at (0, 0)
C) vertical tangent at (0, 0)
D) horizontal tangents at (2, -16), (-2, 16) and vertical tangents at (2, 11), (-2, -11)
E) no horizontal or vertical tangents
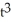 - 3t, y =
- 3t, y = 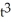 - 12t have horizontal and vertical tangents.
- 12t have horizontal and vertical tangents.A) horizontal tangents at (2, 11), (-2, -11) and vertical tangents at (2, -16), (-2, 16)
B) horizontal tangent at (0, 0)
C) vertical tangent at (0, 0)
D) horizontal tangents at (2, -16), (-2, 16) and vertical tangents at (2, 11), (-2, -11)
E) no horizontal or vertical tangents

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
43
Find equations of the three normal lines to the parabola given parametrically by the equations
x(t) =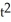 , y(t) = 2t, which pass through the point P (3, 0).
, y(t) = 2t, which pass through the point P (3, 0).
x(t) =
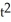 , y(t) = 2t, which pass through the point P (3, 0).
, y(t) = 2t, which pass through the point P (3, 0).
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
44
Find 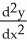 at the highest point on the cycloid x = a
at the highest point on the cycloid x = a
- a sin
, y = a - a cos
.
A) -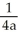
B) -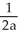
C)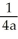
D)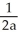
E)
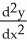 at the highest point on the cycloid x = a
at the highest point on the cycloid x = a - a sin
, y = a - a cos
.
A) -
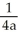
B) -
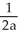
C)
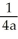
D)
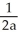
E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
45
Find the slope of the curve x = 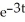 sin 2t, y =
sin 2t, y = 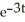 cos 3t at t = 0.
cos 3t at t = 0.
A) -
B) -
C) 0
D)
E)
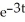 sin 2t, y =
sin 2t, y = 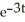 cos 3t at t = 0.
cos 3t at t = 0.A) -

B) -

C) 0
D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
46
Find the coordinates of the highest point of the curve x = 6t, y = 6t - 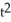 .
.
A) (18, 9)
B) (0, 0)
C) (12, 6)
D) (6, 5)
E) (24, 8)
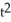 .
.A) (18, 9)
B) (0, 0)
C) (12, 6)
D) (6, 5)
E) (24, 8)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
47
Find the slopes of two lines tangent to the parametric curve x = 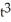 +
+ 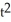 - 6t + 1,y =
- 6t + 1,y = 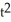 + t - 4 at the point
+ t - 4 at the point 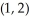 on the curve.
on the curve.
A) 2, -3
B) - ,
, 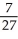
C) -6, -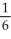
D) , -
, - 
E) - ,
, 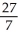
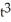 +
+ 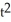 - 6t + 1,y =
- 6t + 1,y = 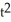 + t - 4 at the point
+ t - 4 at the point 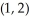 on the curve.
on the curve.A) 2, -3
B) -
 ,
, 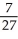
C) -6, -
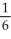
D)
 , -
, - 
E) -
 ,
, 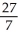

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
48
Where does the curve x = 2 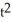 - 5, y =
- 5, y = 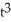 + t have a tangent line that is perpendicular to the line
+ t have a tangent line that is perpendicular to the line 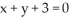 ?
?
A)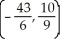 and (-3, 2)
and (-3, 2)
B)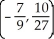 and (3, -2)
and (3, -2)
C)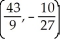 and (3, -2)
and (3, -2)
D)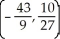 and (-3, 2)
and (-3, 2)
E)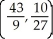 and (-3, -2)
and (-3, -2)
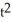 - 5, y =
- 5, y = 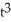 + t have a tangent line that is perpendicular to the line
+ t have a tangent line that is perpendicular to the line 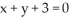 ?
?A)
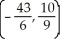 and (-3, 2)
and (-3, 2)B)
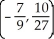 and (3, -2)
and (3, -2)C)
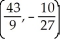 and (3, -2)
and (3, -2)D)
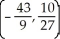 and (-3, 2)
and (-3, 2)E)
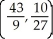 and (-3, -2)
and (-3, -2)
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
49
Where is the curve x = ln t, y = et concave upward?
A) at all points on the curve
B) at all points corresponding to values of t satisfying t > 1
C) at all points corresponding to values of t satisfying 0 < t < 1
D) at all points corresponding to values of t satisfying 0 < t 1
E) nowhere
A) at all points on the curve
B) at all points corresponding to values of t satisfying t > 1
C) at all points corresponding to values of t satisfying 0 < t < 1
D) at all points corresponding to values of t satisfying 0 < t 1
E) nowhere

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
50
Find the slope of the curve x = 3 csc(t), y = 2 cot(t) at the point t = 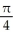 .
.
A)
B) -
C) -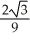
D)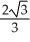
E)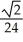
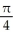 .
.A)

B) -

C) -
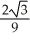
D)
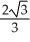
E)
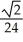

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
51
Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by the equations x(t) = 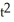 + 2t + 2, y(t) = 1 - 3
+ 2t + 2, y(t) = 1 - 3 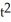 - 2
- 2 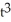 at the point on the curve where t = -1.
at the point on the curve where t = -1.
A) x -3y -1 = 0
B) y =1
C) y = x + 1
D) 3x -y -3 = 0
E) y = 3x -7
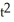 + 2t + 2, y(t) = 1 - 3
+ 2t + 2, y(t) = 1 - 3 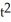 - 2
- 2 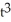 at the point on the curve where t = -1.
at the point on the curve where t = -1.A) x -3y -1 = 0
B) y =1
C) y = x + 1
D) 3x -y -3 = 0
E) y = 3x -7

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
52
At what values of t does the curve x = t - sin t, y = 1 - cos t have (a) a horizontal tangent, (b) a vertical tangent, and (c) no tangent?
A) (a) t = 2k , k is an integer; (b) t = (2k + 1) ; (c) nowhere
B) (a) t = k , k is an integer; (b) nowhere; (c) nowhere
C) (a) t = (2k + 1) , k is an integer; (b) t = 2k , k is an integer; (c) nowhere
D) (a) t = (2k + 1) , k is an integer; (b) nowhere; (c) t = 2k , k is an integer
E) (a) t = k , k is an integer; (b) t = 2k , k is an integer; (c) nowhere
A) (a) t = 2k , k is an integer; (b) t = (2k + 1) ; (c) nowhere
B) (a) t = k , k is an integer; (b) nowhere; (c) nowhere
C) (a) t = (2k + 1) , k is an integer; (b) t = 2k , k is an integer; (c) nowhere
D) (a) t = (2k + 1) , k is an integer; (b) nowhere; (c) t = 2k , k is an integer
E) (a) t = k , k is an integer; (b) t = 2k , k is an integer; (c) nowhere

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
53
Find the tangent line(s) to the parametric curve given by x = 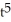 - 4
- 4 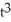 , y=
, y= 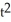 at (0, 4).
at (0, 4).
A) y = 4 ± x
x
B) y = 4 ±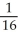 x
x
C) y = 8 ± x
x
D) y = 8 ±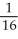 x
x
E) y = 2 ± x
x
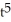 - 4
- 4 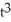 , y=
, y= 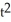 at (0, 4).
at (0, 4).A) y = 4 ±
 x
xB) y = 4 ±
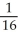 x
xC) y = 8 ±
 x
xD) y = 8 ±
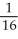 x
xE) y = 2 ±
 x
x
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
54
Determine the coordinates of the points where the curve x = 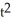 + 2t, y = 2
+ 2t, y = 2 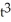 + 7 has (a) a horizontal tangent and (b) a vertical tangent.
+ 7 has (a) a horizontal tangent and (b) a vertical tangent.
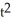 + 2t, y = 2
+ 2t, y = 2 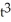 + 7 has (a) a horizontal tangent and (b) a vertical tangent.
+ 7 has (a) a horizontal tangent and (b) a vertical tangent.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
55
Determine the coordinates of the points where the curve x = 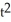 + 2t, y = 2
+ 2t, y = 2 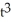 + 7 has (a) a horizontal tangent and (b) a vertical tangent.
+ 7 has (a) a horizontal tangent and (b) a vertical tangent.
A) (a) (0, -9) (b) (±2, -6)
B) (a) (-2, -9) (b) (-2, -6)
C) (a) (2, -9) (b) (2, -6)
D) (a) (0, -9) (b) (2, 6)
E) (a) (2, 9) (b) (2, 6)
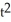 + 2t, y = 2
+ 2t, y = 2 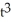 + 7 has (a) a horizontal tangent and (b) a vertical tangent.
+ 7 has (a) a horizontal tangent and (b) a vertical tangent.A) (a) (0, -9) (b) (±2, -6)
B) (a) (-2, -9) (b) (-2, -6)
C) (a) (2, -9) (b) (2, -6)
D) (a) (0, -9) (b) (2, 6)
E) (a) (2, 9) (b) (2, 6)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
56
Find the arc length of x = u, y = 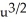 , 0 u
, 0 u  .
.
A)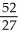 units
units
B) 2 units
C)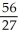 units
units
D)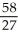 units
units
E)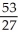 units
units
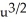 , 0 u
, 0 u  .
.A)
 units
unitsB) 2 units
C)
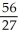 units
unitsD)
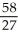 units
unitsE)
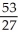 units
units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
57
Find the length of the curve x = cos t + sin t, y = sin t - cos t, from t = 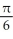 to t =
to t = 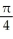 .
.
A)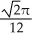 units
units
B)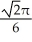 units
units
C)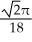 units
units
D)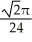 units
units
E)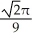 units
units
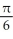 to t =
to t = 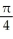 .
.A)
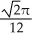 units
unitsB)
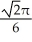 units
unitsC)
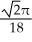 units
unitsD)
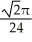 units
unitsE)
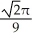 units
units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
58
Find the length of x = ln sin , y = , 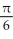
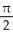 .
.
A) ln (4 -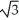 ) units
) units
B) ln (3 +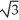 ) units
) units
C) ln (2 +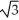 ) units
) units
D) ln (1 + 2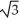 ) units
) units
E) ln (1 - 3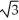 ) units
) units
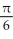
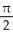 .
.A) ln (4 -
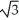 ) units
) unitsB) ln (3 +
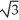 ) units
) unitsC) ln (2 +
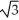 ) units
) unitsD) ln (1 + 2
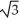 ) units
) unitsE) ln (1 - 3
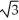 ) units
) units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
59
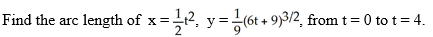
A) 10 units
B) 15 units
C) 20 units
D) 25 units
E) 16 units

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
60
Find the arc length of the curve x = et sin t, y = et cos t, from t = - 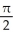 to t =
to t = 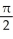 .
.
A)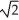
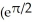 - 1) units
- 1) units
B) 2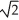
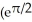 + 1) units
+ 1) units
C) 2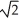
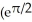 - 1) units
- 1) units
D) 2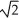 sinh
sinh 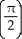 units
units
E) 2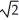 cosh
cosh 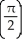 units
units
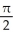 to t =
to t = 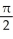 .
.A)
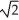
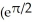 - 1) units
- 1) unitsB) 2
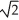
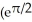 + 1) units
+ 1) unitsC) 2
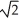
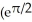 - 1) units
- 1) unitsD) 2
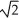 sinh
sinh 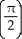 units
unitsE) 2
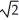 cosh
cosh 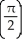 units
units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
61
Find the arc length of the curve x =  ln (1 +
ln (1 + 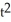 ), y =
), y = 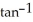 t, from t = 0 to t = 1.
t, from t = 0 to t = 1.
A) ln (2 -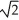 ) units
) units
B) ln (3 -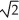 ) units
) units
C) ln (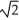 + 1) units
+ 1) units
D) ln (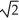 - 1) units
- 1) units
E) ln (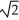 ) units
) units
 ln (1 +
ln (1 + 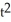 ), y =
), y = 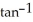 t, from t = 0 to t = 1.
t, from t = 0 to t = 1.A) ln (2 -
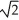 ) units
) unitsB) ln (3 -
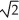 ) units
) unitsC) ln (
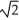 + 1) units
+ 1) unitsD) ln (
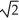 - 1) units
- 1) unitsE) ln (
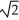 ) units
) units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
62
Find the length of one arch of the cycloid x = a( - sin ), y = a(1 - cos ).
A) 8a units
B) 10a units
C) 12a units
D) 6a units
E) 4a units
A) 8a units
B) 10a units
C) 12a units
D) 6a units
E) 4a units

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
63
Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t ![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 2 ] about the x-axis.
[0, 2 ] about the x-axis.
A)![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a2_a0f8_1106276dab3c_TB9661_11.jpg) square units
square units
B)![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a3_a0f8_7ff8dc7328c8_TB9661_11.jpg) square units
square units
C)![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a4_a0f8_df56c035bc9d_TB9661_11.jpg) square units
square units
D)![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a5_a0f8_996ae5294fa5_TB9661_11.jpg) square units
square units
E) 64 square units
![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 2 ] about the x-axis.
[0, 2 ] about the x-axis.A)
![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a2_a0f8_1106276dab3c_TB9661_11.jpg) square units
square unitsB)
![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a3_a0f8_7ff8dc7328c8_TB9661_11.jpg) square units
square unitsC)
![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a4_a0f8_df56c035bc9d_TB9661_11.jpg) square units
square unitsD)
![<strong>Find the area of the surface generated by rotating x = t - sin t, y = 1 - cos t where t [0, 2 \pi ] about the x-axis.</strong> A) square units B) square units C) square units D) square units E) 64 \pi square units](https://storage.examlex.com/TB9661/11ee77e1_77d5_c8a5_a0f8_996ae5294fa5_TB9661_11.jpg) square units
square unitsE) 64 square units

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
64
Find the area of the surface generated by rotating the astroid x = a 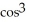 t, y = a
t, y = a 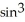 t about
t about 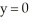 .
.
A)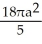 square units
square units
B)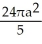 square units
square units
C)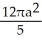 square units
square units
D)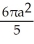 square units
square units
E)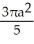 square units
square units
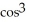 t, y = a
t, y = a 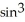 t about
t about 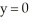 .
.A)
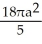 square units
square unitsB)
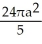 square units
square unitsC)
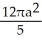 square units
square unitsD)
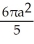 square units
square unitsE)
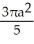 square units
square units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
65
Find the area of the surface generated by rotating x = 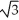
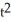 , y =
, y = 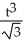 , 0 t 1 about the y-axis.
, 0 t 1 about the y-axis.
A) 4 (5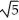 - 8) square units
- 8) square units
B) 4 (5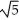 + 8) square units
+ 8) square units
C) 2 (5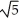 - 8) square units
- 8) square units
D) 2 (5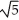 + 8) square units
+ 8) square units
E) (5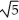 - 8) square units
- 8) square units
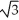
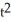 , y =
, y = 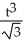 , 0 t 1 about the y-axis.
, 0 t 1 about the y-axis.A) 4 (5
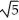 - 8) square units
- 8) square unitsB) 4 (5
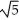 + 8) square units
+ 8) square unitsC) 2 (5
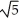 - 8) square units
- 8) square unitsD) 2 (5
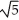 + 8) square units
+ 8) square unitsE) (5
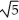 - 8) square units
- 8) square units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
66
Find the length of the curve x = 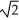 t, y =
t, y = 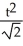 , 0 t 1.
, 0 t 1.
A) 1 +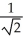 ln(
ln( 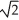 + 1) units
+ 1) units
B)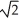 +
+ 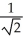 ln(
ln( 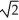 + 1) units
+ 1) units
C)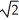 -
- 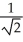 ln(
ln( 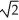 + 1) units
+ 1) units
D) 1 -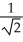 ln(
ln( 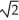 + 1) units
+ 1) units
E) 1 +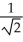 ln(
ln( 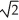 ) units
) units
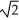 t, y =
t, y = 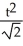 , 0 t 1.
, 0 t 1.A) 1 +
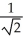 ln(
ln( 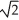 + 1) units
+ 1) unitsB)
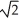 +
+ 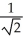 ln(
ln( 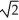 + 1) units
+ 1) unitsC)
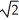 -
- 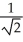 ln(
ln( 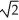 + 1) units
+ 1) unitsD) 1 -
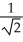 ln(
ln( 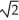 + 1) units
+ 1) unitsE) 1 +
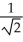 ln(
ln( 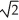 ) units
) units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
67
Find the area of the surface generated by rotating x = 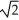 t, y =
t, y = 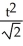 , 0 t 1, about the x-axis.
, 0 t 1, about the x-axis.
A)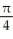
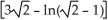 square units
square units
B)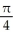
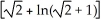 square units
square units
C)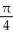
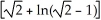 square units
square units
D)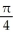
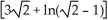 square units
square units
E)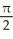
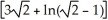 square units
square units
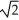 t, y =
t, y = 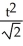 , 0 t 1, about the x-axis.
, 0 t 1, about the x-axis.A)
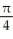
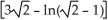 square units
square unitsB)
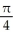
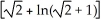 square units
square unitsC)
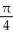
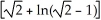 square units
square unitsD)
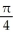
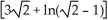 square units
square unitsE)
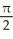
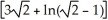 square units
square units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
68
Find the arc length of the curve x = 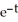 , y =
, y = 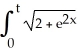 dx, 0 ≤ t ≤ ln(2).
dx, 0 ≤ t ≤ ln(2).
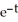 , y =
, y = 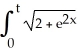 dx, 0 ≤ t ≤ ln(2).
dx, 0 ≤ t ≤ ln(2).
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
69
Find the arc length x = 2 cos + cos 2 + 1, y = 2 sin + sin 2 , for 0 2 .
A) 12 units
B) 14 units
C) 16 units
D) 18 units
E) 10 units
A) 12 units
B) 14 units
C) 16 units
D) 18 units
E) 10 units

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
70
Find the area of the region bounded by the ellipse x = 7 cos
, y = 9 sin .
A) 63 square units
B) 16 square units
C) 2 square units
D) 25 square units
E) 72 square units
, y = 9 sin .
A) 63 square units
B) 16 square units
C) 2 square units
D) 25 square units
E) 72 square units

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
71
Find the area of the region bounded by the hypocycloid x = a 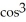
, y = a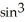
.
A)
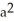 square units
square units
B)
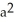 square units
square units
C)
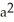 square units
square units
D)
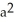 square units
square units
E)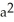 square units
square units
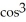
, y = a
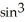
.
A)

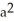 square units
square unitsB)

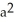 square units
square unitsC)

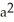 square units
square unitsD)

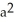 square units
square unitsE)
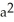 square units
square units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the area above the x-axis and under one arch of the cycloid x = a(t - sin t), y = a(1 - cos t).
A) 2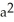 square units
square units
B) 3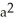 square units
square units
C) 4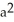 square units
square units
D) 6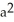 square units
square units
E) 5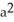 square units
square units
A) 2
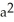 square units
square unitsB) 3
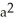 square units
square unitsC) 4
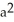 square units
square unitsD) 6
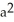 square units
square unitsE) 5
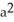 square units
square units
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
73
Find the rectangular coordinates of the point with polar coordinates 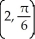 .
.
A) (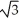 , 1)
, 1)
B) (1,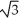 )
)
C) (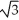 , 2)
, 2)
D) (2,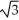 )
)
E) (3, 1)
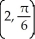 .
.A) (
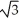 , 1)
, 1)B) (1,
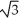 )
)C) (
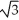 , 2)
, 2)D) (2,
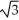 )
)E) (3, 1)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
74
Convert the point with Cartesian coordinates (-1, -1) to polar coordinates.
A)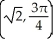
B)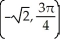
C)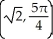
D)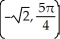
E)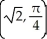
A)
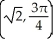
B)
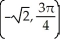
C)
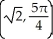
D)
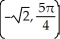
E)
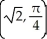

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
75
Find a rectangular equation equivalent to the polar equation
=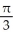 .
.
A) y = x
B) y =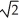 x
x
C) y =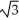 x
x
D) y = 2x
E) y = 3x
=
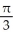 .
.A) y = x
B) y =
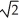 x
xC) y =
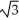 x
xD) y = 2x
E) y = 3x

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
76
Find a rectangular equation equivalent to the polar equation r = tan
.
A)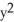 =
= 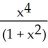
B)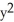 =
= 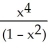
C)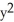 =
= 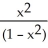
D)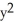 =
= 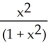
E)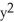 =
= 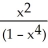
.
A)
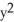 =
= 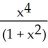
B)
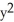 =
= 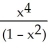
C)
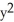 =
= 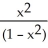
D)
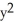 =
= 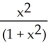
E)
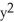 =
= 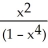

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
77
The equation of a conic section in polar coordinates is given by r = 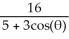 .(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
.(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
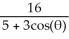 .(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
.(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
78
Convert x2 + y2 = xy to polar coordinates.
A) r2 =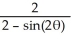
B) r =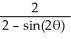
C) r =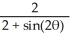
D) r2 =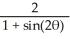
E) r2 =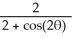
A) r2 =
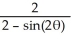
B) r =
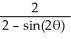
C) r =
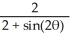
D) r2 =
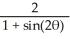
E) r2 =
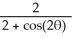

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
79
Describe the plane curve represented in polar coordinates (r , ) by the equation r = 4 sin( ) , ![<strong>Describe the plane curve represented in polar coordinates (r , \theta ) by the equation r = 4 sin( \theta ) , \theta [0 , \theta ].</strong> A) a straight line through the origin of slope 4 B) a circle centred at (x , y) = (2 , 0) and is of radius 2 C) a circle centred at (x , y) = (0 , 2) and is of radius 2 D) a circle centred at (x , y) = (0 , 2) and is of radius 4 E) a circle centred at (x , y) = (2 , 0) and is of radius 4](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0 , ].
[0 , ].
A) a straight line through the origin of slope 4
B) a circle centred at (x , y) = (2 , 0) and is of radius 2
C) a circle centred at (x , y) = (0 , 2) and is of radius 2
D) a circle centred at (x , y) = (0 , 2) and is of radius 4
E) a circle centred at (x , y) = (2 , 0) and is of radius 4
![<strong>Describe the plane curve represented in polar coordinates (r , \theta ) by the equation r = 4 sin( \theta ) , \theta [0 , \theta ].</strong> A) a straight line through the origin of slope 4 B) a circle centred at (x , y) = (2 , 0) and is of radius 2 C) a circle centred at (x , y) = (0 , 2) and is of radius 2 D) a circle centred at (x , y) = (0 , 2) and is of radius 4 E) a circle centred at (x , y) = (2 , 0) and is of radius 4](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0 , ].
[0 , ].A) a straight line through the origin of slope 4
B) a circle centred at (x , y) = (2 , 0) and is of radius 2
C) a circle centred at (x , y) = (0 , 2) and is of radius 2
D) a circle centred at (x , y) = (0 , 2) and is of radius 4
E) a circle centred at (x , y) = (2 , 0) and is of radius 4

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
80
Describe the graph of the polar equation r = 6(sin + cos ).
A) Straight line with intercepts (6, 0) and (0, 6)
B) Circle with centre at (3, 3) and radius 6
C) Circle with centre at (3, 3) and radius 3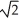
D) Straight line with intercepts (3, 0) and (0, 3)
E) Circle with centre at (3, 3) and radius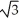
A) Straight line with intercepts (6, 0) and (0, 6)
B) Circle with centre at (3, 3) and radius 6
C) Circle with centre at (3, 3) and radius 3
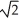
D) Straight line with intercepts (3, 0) and (0, 3)
E) Circle with centre at (3, 3) and radius
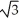

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck


