Deck 4: Transcendental Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 4: Transcendental Functions
1
Which of the following functions is/are one-to-one?
(a)![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07c8_a0f8_710f06ff1fdd_TB9661_11.jpg) , (b) 1 -
, (b) 1 - ![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07c9_a0f8_eb17941b460d_TB9661_11.jpg) , (c)
, (c) ![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07ca_a0f8_895213fbf3ac_TB9661_11.jpg) sgn(x), (d) cos(x) on [0, ], (e) sin(x) on [0, ].
sgn(x), (d) cos(x) on [0, ], (e) sin(x) on [0, ].
A) only (c) and (d)
B) only (d)
C) only (c) and (e)
D) only (a) and (b)
E) none of the above
(a)
![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07c8_a0f8_710f06ff1fdd_TB9661_11.jpg) , (b) 1 -
, (b) 1 - ![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07c9_a0f8_eb17941b460d_TB9661_11.jpg) , (c)
, (c) ![<strong>Which of the following functions is/are one-to-one? (a) , (b) 1 - , (c) sgn(x), (d) cos(x) on [0, \pi ], (e) sin(x) on [0, \pi ].</strong> A) only (c) and (d) B) only (d) C) only (c) and (e) D) only (a) and (b) E) none of the above](https://storage.examlex.com/TB9661/11ee77e1_7831_07ca_a0f8_895213fbf3ac_TB9661_11.jpg) sgn(x), (d) cos(x) on [0, ], (e) sin(x) on [0, ].
sgn(x), (d) cos(x) on [0, ], (e) sin(x) on [0, ].A) only (c) and (d)
B) only (d)
C) only (c) and (e)
D) only (a) and (b)
E) none of the above
only (c) and (d)
2
Find the inverse of the function f(x) = 3 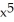 + 7.
+ 7.
A)
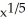 - 7
- 7
B)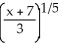
C)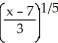
D) 3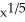 - 7
- 7
E)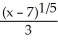
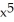 + 7.
+ 7.A)

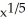 - 7
- 7B)
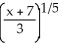
C)
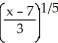
D) 3
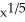 - 7
- 7E)
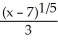
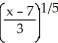
3
Assume that the function F(x) = 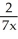 -
-  , x
, x  (0 , ) has an inverse. Find a formula for
(0 , ) has an inverse. Find a formula for 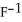 (x).
(x).
A)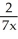 -
- 
B)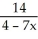
C) x - 2
x - 2
D)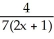
E) 7x - 2
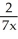 -
-  , x
, x  (0 , ) has an inverse. Find a formula for
(0 , ) has an inverse. Find a formula for  (x).
(x).A)
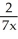 -
- 
B)
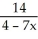
C)
 x - 2
x - 2D)
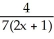
E) 7x - 2
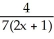
4
Which of the following functions has an inverse?
(a)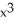 + x - 1, (b)
+ x - 1, (b) 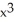 - x + 1, (c)
- x + 1, (c) 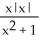 , (d) 4
, (d) 4 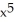 +
+ 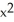 - 15, (e)
- 15, (e) 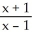
A) only (a)
B) only (c) and (e)
C) only (a), (c), and (e)
D) only (a) and (b)
E) none of the above
(a)
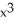 + x - 1, (b)
+ x - 1, (b) 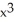 - x + 1, (c)
- x + 1, (c) 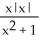 , (d) 4
, (d) 4 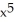 +
+ 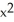 - 15, (e)
- 15, (e) 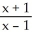
A) only (a)
B) only (c) and (e)
C) only (a), (c), and (e)
D) only (a) and (b)
E) none of the above

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
If f is one-to-one, and if f(1) = 3, f(2) = 4, f(3) = 5, f(4) = 8, and f(5) = 20, find 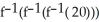 .
.
A) 2
B) 1
C) 3
D) 8
E) 4
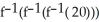 .
.A) 2
B) 1
C) 3
D) 8
E) 4

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
Find the inverse of the function f(x) =  where -5 x 0.
where -5 x 0.
A)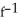 (x) = -
(x) = -  , where 0 x 5
, where 0 x 5
B)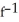 (x) =
(x) =  , where 0 x 5
, where 0 x 5
C)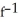 (x) = -
(x) = -  , where -5 x 0
, where -5 x 0
D)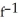 (x) =
(x) =  , where -5 x 0
, where -5 x 0
E)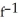 (x) =
(x) = 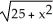 , where 0 x 5
, where 0 x 5
 where -5 x 0.
where -5 x 0.A)
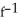 (x) = -
(x) = -  , where 0 x 5
, where 0 x 5B)
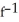 (x) =
(x) =  , where 0 x 5
, where 0 x 5C)
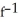 (x) = -
(x) = -  , where -5 x 0
, where -5 x 0D)
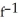 (x) =
(x) =  , where -5 x 0
, where -5 x 0E)
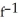 (x) =
(x) = 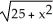 , where 0 x 5
, where 0 x 5
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
7
Find the inverse of the following function: f(x) = 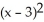 , if x 3.
, if x 3.
A)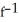 (x) = 3 +
(x) = 3 + 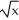
B)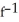 (x) = 3 -
(x) = 3 - 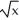
C)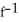 (x) = 2 +
(x) = 2 + 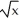
D)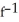 (x) = 1 +
(x) = 1 + 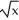
E)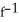 (x) =
(x) = 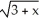
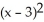 , if x 3.
, if x 3.A)
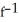 (x) = 3 +
(x) = 3 + 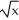
B)
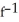 (x) = 3 -
(x) = 3 - 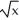
C)
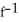 (x) = 2 +
(x) = 2 + 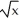
D)
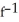 (x) = 1 +
(x) = 1 + 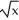
E)
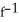 (x) =
(x) = 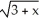

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
Find the inverse of the function f(x) = 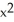 - 8x + 4, where x 4. State its domain.
- 8x + 4, where x 4. State its domain.
A)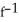 (x) = 4 -
(x) = 4 - 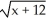 . Domain is x -12.
. Domain is x -12.
B)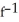 (x) = 4 +
(x) = 4 + 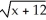 . Domain is x -12.
. Domain is x -12.
C)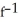 (x) = 4 +
(x) = 4 + 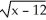 . Domain is x 12.
. Domain is x 12.
D)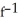 (x) = 4 -
(x) = 4 - 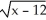 . Domain is x 12.
. Domain is x 12.
E) f(x) has no inverse.
 - 8x + 4, where x 4. State its domain.
- 8x + 4, where x 4. State its domain.A)
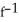 (x) = 4 -
(x) = 4 - 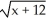 . Domain is x -12.
. Domain is x -12.B)
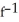 (x) = 4 +
(x) = 4 + 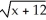 . Domain is x -12.
. Domain is x -12.C)
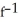 (x) = 4 +
(x) = 4 + 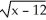 . Domain is x 12.
. Domain is x 12.D)
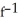 (x) = 4 -
(x) = 4 - 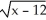 . Domain is x 12.
. Domain is x 12.E) f(x) has no inverse.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
Find the inverse of the following function: f(x) = 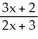 .
.
A)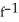 (x) =
(x) = 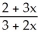
B) (x) =
(x) = 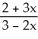
C) (x) =
(x) = 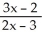
D) (x) =
(x) = 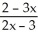
E) f(x) has no inverse.
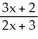 .
.A)
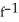 (x) =
(x) = 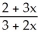
B)
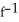 (x) =
(x) = 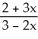
C)
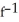 (x) =
(x) = 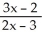
D)
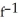 (x) =
(x) = 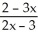
E) f(x) has no inverse.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
Let g be the inverse function of f and let y = 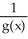 . Calculate
. Calculate 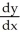 at x =
at x =  given that f(6) =
given that f(6) =  ,
, 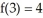 ,
, 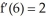 , and
, and 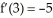 .
.
A) -
B) -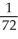
C) -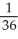
D)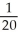
E)
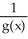 . Calculate
. Calculate 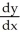 at x =
at x =  given that f(6) =
given that f(6) =  ,
, 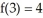 ,
, 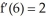 , and
, and 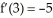 .
.A) -

B) -
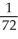
C) -
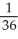
D)
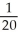
E)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
Let f(x) = 2 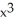 + 3
+ 3 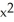 +5, x 0, and let y = g(x) be the equation of its inverse function.Find the x and y coordinates of all points on the graph of y = g(x) where the tangent line has slope
+5, x 0, and let y = g(x) be the equation of its inverse function.Find the x and y coordinates of all points on the graph of y = g(x) where the tangent line has slope
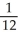 .
.
A) (1, 10)
B) (1, -2)
C) (-2, 1)
D) (10, 1)
E) (1, -2) and (10, 1)
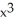 + 3
+ 3 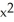 +5, x 0, and let y = g(x) be the equation of its inverse function.Find the x and y coordinates of all points on the graph of y = g(x) where the tangent line has slope
+5, x 0, and let y = g(x) be the equation of its inverse function.Find the x and y coordinates of all points on the graph of y = g(x) where the tangent line has slope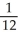 .
.A) (1, 10)
B) (1, -2)
C) (-2, 1)
D) (10, 1)
E) (1, -2) and (10, 1)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
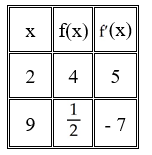
12
Let g be the inverse function of f . Use the table of values below to compute 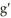 (
(  ).
). 
A) 2
B)
C) -
D)
E)
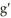 (
(  ).
). 

A) 2
B)

C) -

D)

E)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
The function f(x) = 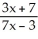 is
is
A function f is self-inverse if -1 (x) = f(x) for all x in domain f.
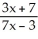 is
is A function f is self-inverse if -1 (x) = f(x) for all x in domain f.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
An even function defined on (- , ) may have an inverse.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
Prove that if an odd function f(x) is one-to-one, the inverse function g(y) is also odd.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
Let f(x) = 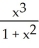 for all x. Is f invertible? Why? Find
for all x. Is f invertible? Why? Find 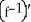
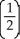 .
.
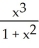 for all x. Is f invertible? Why? Find
for all x. Is f invertible? Why? Find 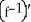
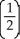 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
Simplify the expression 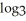 (
( 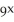 ) -
) - 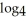 (
( 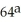 ).
).
A) 3x - 3a
B) 9x - 64a
C)
D) 3x - 4a
E)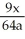
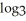 (
( 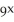 ) -
) - 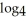 (
( 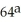 ).
).A) 3x - 3a
B) 9x - 64a
C)

D) 3x - 4a
E)
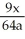

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
Given that 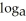 (5) = 0.02, evaluate
(5) = 0.02, evaluate 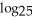 (a).
(a).
A) 25
B) 5
C) 5a
D) 50
E) 25a
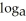 (5) = 0.02, evaluate
(5) = 0.02, evaluate 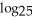 (a).
(a).A) 25
B) 5
C) 5a
D) 50
E) 25a

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
Simplify the expression 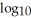 (20) +
(20) + 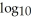 (5).
(5).
A) 2
B)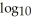 (25)
(25)
C) 2.5
D) 4
E)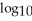 (15)
(15)
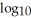 (20) +
(20) + 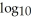 (5).
(5).A) 2
B)
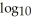 (25)
(25)C) 2.5
D) 4
E)
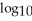 (15)
(15)
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
Simplify the expression - 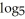
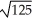 -
- 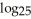 (5)
(5)
A) 1
B) 2
C) 5
D) 25
E)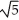
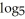
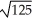 -
- 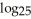 (5)
(5)A) 1
B) 2
C) 5
D) 25
E)
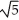

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
If 4 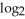 x -
x - 
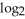 (
( 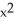 + 1) +
+ 1) + 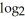 (x - 1) =
(x - 1) = 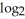 (y), find y.
(y), find y.
A)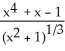
B)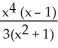
C)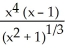
D)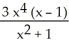
E)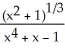
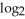 x -
x - 
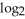 (
( 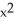 + 1) +
+ 1) + 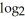 (x - 1) =
(x - 1) = 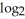 (y), find y.
(y), find y.A)
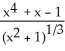
B)
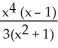
C)
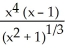
D)
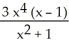
E)
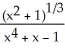

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the exponential equation 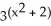 = 81.
= 81.
A) x = ±1
B) x = ±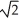
C) x = 0
D) x = ±2
E) x = ±4
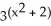 = 81.
= 81.A) x = ±1
B) x = ±
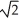
C) x = 0
D) x = ±2
E) x = ±4

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the exponential equation = 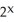
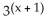 108.
108.
A) x = 2
B) x = 1
C) x = -1
D) x = -2
E) x = 3
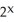
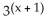 108.
108.A) x = 2
B) x = 1
C) x = -1
D) x = -2
E) x = 3

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
Let f(x) = ![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_9b2a_a0f8_2d50e1049195_TB9661_11.jpg) .
.
The domain of f is the set of all real numbers x such that:
A) x![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) (- , 1]
(- , 1] ![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_c23b_a0f8_7f1bb618c043_TB9661_11.jpg)
B) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (1 , 3)
C) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [3 , )
D) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 1)![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_c23c_a0f8_f1aac966613d_TB9661_11.jpg)
E) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [1 , 3]
![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_9b2a_a0f8_2d50e1049195_TB9661_11.jpg) .
.The domain of f is the set of all real numbers x such that:
A) x
![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) (- , 1]
(- , 1] ![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_c23b_a0f8_7f1bb618c043_TB9661_11.jpg)
B) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (1 , 3)
C) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [3 , )
D) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 1)
![<strong>Let f(x) = . The domain of f is the set of all real numbers x such that:</strong> A) x (- \infty , 1] B) x (1 , 3) C) x [3 , \infty ) D) x (- \infty , 1) E) x [1 , 3]](https://storage.examlex.com/TB9661/11ee77e1_7835_c23c_a0f8_f1aac966613d_TB9661_11.jpg)
E) x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [1 , 3]

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the exponential equation 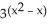 = 9.
= 9.
A) -2, -1
B) 2, 1
C) 2, -1
D) 2, -2
E) none of the above
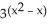 = 9.
= 9.A) -2, -1
B) 2, 1
C) 2, -1
D) 2, -2
E) none of the above

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
If 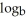 1296 = 4, what is
1296 = 4, what is 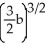 ?
?
A) 29
B) 33
C) 28
D) 27
E) 25
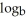 1296 = 4, what is
1296 = 4, what is 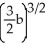 ?
?A) 29
B) 33
C) 28
D) 27
E) 25

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the equation 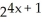 -
- 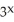 = 0 correct to 3 decimal places.
= 0 correct to 3 decimal places.
A) -1.414
B) -0.414
C) 0.414
D) 1.414
E) none of the above
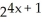 -
- 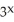 = 0 correct to 3 decimal places.
= 0 correct to 3 decimal places.A) -1.414
B) -0.414
C) 0.414
D) 1.414
E) none of the above

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the logarithmic equation 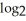 (
( 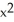 - 6x) = 3 +
- 6x) = 3 + 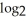 (1 - x).
(1 - x).
A) only -4
B) only 2
C) -4 and 2
D) only 1
E) 1 and 2
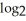 (
( 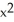 - 6x) = 3 +
- 6x) = 3 + 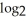 (1 - x).
(1 - x).A) only -4
B) only 2
C) -4 and 2
D) only 1
E) 1 and 2

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the logarithmic equation 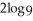 (
( 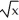 ) -
) - 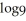 (6x - 1) = 0.
(6x - 1) = 0.
A)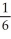
B)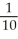
C)
D)
E)
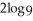 (
( 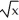 ) -
) - 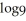 (6x - 1) = 0.
(6x - 1) = 0.A)
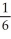
B)
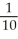
C)

D)

E)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the logarithmic equation log x = 1 - log (x -3).
A) only -5
B) only 5
C) only -2
D) 5 and -2
E) -5 and -2
A) only -5
B) only 5
C) only -2
D) 5 and -2
E) -5 and -2

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the logarithmic equation 2 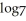 (
( 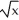 ) -
) - 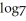 (2 -
(2 - 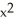 ) = 0.
) = 0.
A) x = 1
B) x = 1 and x = -2
C) x = -2
D) x = 0
E) x = -1
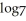 (
( 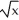 ) -
) - 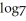 (2 -
(2 - 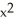 ) = 0.
) = 0.A) x = 1
B) x = 1 and x = -2
C) x = -2
D) x = 0
E) x = -1

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate ln 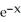 .
.
A) -x
B) x
C) 1
D) -1
E) 0
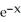 .
.A) -x
B) x
C) 1
D) -1
E) 0

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
33
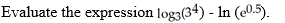
A) 4.5
B) 6.6
C) 3.5
D) 2.2
E) 5.5

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the expression exp(ln3 - ln10).
A)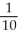
B)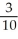
C) -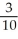
D) 30
E)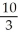
A)
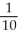
B)
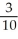
C) -
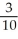
D) 30
E)
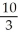

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
Find ln ( 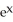 /x).
/x).
A) x + ln x
B) 1 - ln x
C) x - ln x
D)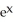 - x
- x
E)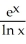
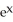 /x).
/x).A) x + ln x
B) 1 - ln x
C) x - ln x
D)
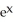 - x
- xE)
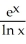

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the exponential equation 5 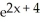 = 8 correct to 3 decimal places.
= 8 correct to 3 decimal places.
A) -1.765
B) 1.755
C) -1.725
D) 1.735
E) 1.693
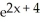 = 8 correct to 3 decimal places.
= 8 correct to 3 decimal places.A) -1.765
B) 1.755
C) -1.725
D) 1.735
E) 1.693

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
Find the roots of the equation 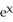 = 2
= 2 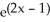 .
.
A) 1 - ln(2)
B)
C) 1
D) ln(2)
E) -ln(2)
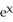 = 2
= 2 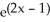 .
.A) 1 - ln(2)
B)

C) 1
D) ln(2)
E) -ln(2)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
Show that for x > 1, 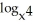 (
( 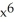 ) =
) =  .
.
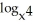 (
( 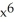 ) =
) =  .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the derivative tan( 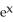 ).
).
A)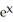
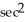 (
( 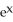 )
)
B) 2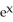
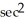 (
( 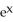 )
)
C)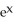 sec (
sec ( 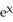 ) tan (
) tan ( 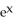 )
)
D)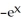 sec (
sec ( 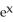 ) tan (
) tan ( 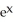 )
)
E)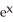
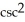 (
( 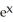 )
)
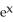 ).
).A)
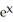
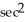 (
( 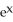 )
)B) 2
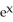
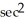 (
( 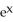 )
)C)
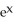 sec (
sec ( 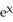 ) tan (
) tan ( 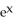 )
)D)
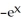 sec (
sec ( 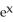 ) tan (
) tan ( 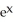 )
)E)
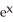
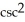 (
( 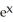 )
)
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
For what value(s) of the constant m is the line y = mx tangent to the curve y = 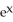 ?
?
A) e
B) 1
C)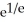
D) ln 2
E)
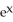 ?
?A) e
B) 1
C)
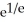
D) ln 2
E)


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
Find a positive number 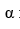 for which the graph of the function f(x) =
for which the graph of the function f(x) = 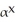 is tangent to the line y = x.
is tangent to the line y = x.
A) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 = e
B) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =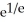
C) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11= 1
D) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =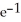
E) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =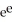
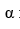 for which the graph of the function f(x) =
for which the graph of the function f(x) = 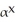 is tangent to the line y = x.
is tangent to the line y = x.A) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 = e
B) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =
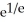
C) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11= 1
D) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =
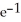
E) 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 =
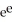

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
Find the slope of the curve 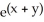 = 2x + y at the point (1, -1).
= 2x + y at the point (1, -1).
A) -2
B) 2
C)
D)
E) undefined
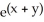 = 2x + y at the point (1, -1).
= 2x + y at the point (1, -1).A) -2
B) 2
C)

D)

E) undefined

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
Find the slope of the curve 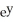 -
- 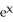 + xy - 1 = 0 at the point (1, 1).
+ xy - 1 = 0 at the point (1, 1).
A)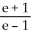
B)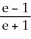
C)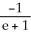
D)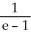
E)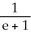
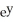 -
- 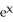 + xy - 1 = 0 at the point (1, 1).
+ xy - 1 = 0 at the point (1, 1).A)
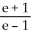
B)
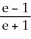
C)
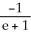
D)
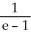
E)
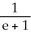

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
Use logarithmic differentiation to find the slope of the line tangent to the curve given by 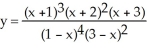 at the point (0,
at the point (0,  ) on the curve.
) on the curve.
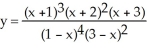 at the point (0,
at the point (0,  ) on the curve.
) on the curve.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the derivative of 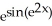 .
.
A) 2cos(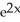 )
) 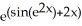
B) 2cos(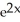 )
) 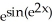
C) cos(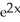 )
) 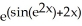
D) cos(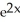 )
) 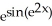
E) -2cos(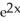 )
) 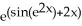
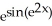 .
.A) 2cos(
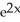 )
) 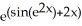
B) 2cos(
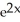 )
) 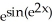
C) cos(
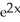 )
) 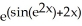
D) cos(
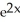 )
) 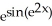
E) -2cos(
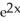 )
) 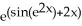

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
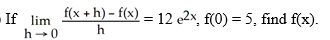
A) 24
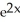 - 19
- 19B) 6
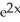 - 1
- 1C)
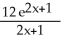 + C, x -
+ C, x - 
D) 10
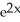 - 5
- 5E) 6
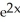 + C
+ C
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate . 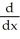
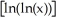
A)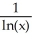
B)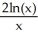
C)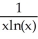
D)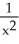
E) 2ln(x)
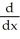
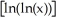
A)
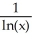
B)
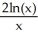
C)
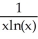
D)
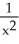
E) 2ln(x)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the antiderivative 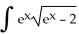 dx.
dx.
A)
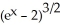 + C
+ C
B)
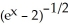 + C
+ C
C)
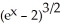 + C
+ C
D)
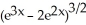 + C
+ C
E)
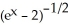 + C
+ C
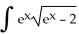 dx.
dx.A)

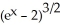 + C
+ CB)

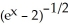 + C
+ CC)

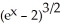 + C
+ CD)

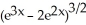 + C
+ CE)

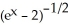 + C
+ C
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
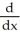
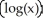 =
= 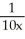 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
The acceleration of an object moving on the x-axis is 9 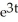 . Find the velocity v if the velocity at time
. Find the velocity v if the velocity at time 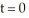 is 4 units per second.
is 4 units per second.
A) v =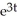 + 3
+ 3
B) v = 27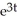 - 23
- 23
C) v = 3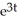 + 1
+ 1
D) v = 9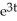 - 5
- 5
E) v =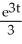 + 1
+ 1
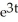 . Find the velocity v if the velocity at time
. Find the velocity v if the velocity at time 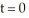 is 4 units per second.
is 4 units per second.A) v =
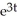 + 3
+ 3B) v = 27
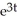 - 23
- 23C) v = 3
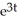 + 1
+ 1D) v = 9
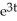 - 5
- 5E) v =
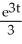 + 1
+ 1
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
Find an equation of the line tangent to the curve 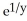 -
- 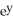 = 2x at the point (0,1).
= 2x at the point (0,1).
A) y = 1 -
B) y = 1 +
C) y = -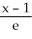
D) y = -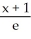
E) y = -1 +
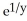 -
- 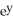 = 2x at the point (0,1).
= 2x at the point (0,1).A) y = 1 -

B) y = 1 +

C) y = -
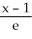
D) y = -
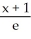
E) y = -1 +


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Find 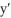 if y =
if y = 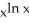 .
.
A) (ln x)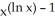
B) 2 (ln x)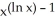
C) 2 (ln x)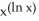
D) 2 (ln x)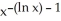
E) (ln x)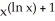
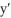 if y =
if y = 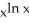 .
.A) (ln x)
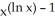
B) 2 (ln x)
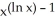
C) 2 (ln x)
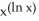
D) 2 (ln x)
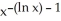
E) (ln x)
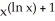

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Find y' if y = 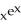 .
.
A)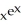 (
( 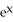 ln(x) +
ln(x) + 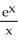 )
)
B)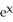 ln(x) +
ln(x) + 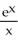
C)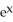
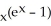
D) ln(x)
E) x(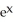 ln(x) +
ln(x) + 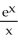 )
)
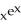 .
.A)
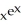 (
( 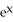 ln(x) +
ln(x) + 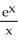 )
)B)
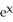 ln(x) +
ln(x) + 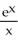
C)
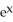
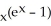
D) ln(x)
E) x(
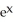 ln(x) +
ln(x) + 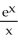 )
)
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
Let f(x) = (2x + 1)(3x + 1)(4x + 1)(5x + 1)(6x + 1). Use logarithmic differentiation to calculate  (0).
(0).
A) 20
B) 1
C) 10
D) 40
E) 5
 (0).
(0).A) 20
B) 1
C) 10
D) 40
E) 5

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the equation 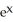 - 2
- 2 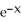 = 1 for x.
= 1 for x.
A) -ln 2
B) ln 4
C) ln 2
D) 1
E) 0
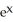 - 2
- 2 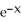 = 1 for x.
= 1 for x.A) -ln 2
B) ln 4
C) ln 2
D) 1
E) 0

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
Find  (173) if f(x) =
(173) if f(x) = 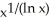 .
.
A) 0
B) e
C) 175
D) 174
E) 1
 (173) if f(x) =
(173) if f(x) = 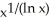 .
.A) 0
B) e
C) 175
D) 174
E) 1

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate . 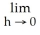
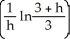
A)
B)
C) -
D) -
E) does not exist
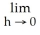
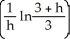
A)

B)

C) -

D) -

E) does not exist

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
The function F(x) = ln 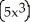 is an antiderivative of the function f(x) =
is an antiderivative of the function f(x) =  .
.
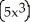 is an antiderivative of the function f(x) =
is an antiderivative of the function f(x) =  .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
Find the derivative of 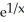 .
.
A) -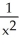
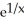
B)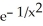
C)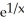
D)
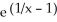
E)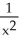
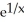
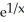 .
.A) -
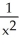
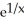
B)
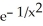
C)
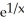
D)

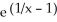
E)
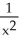
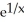

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
Find the derivative of y = ln(sin x).
A) ln (cot x)
B) -ln (cot x)
C) tan x
D) cot x
E) ln(cos x)
A) ln (cot x)
B) -ln (cot x)
C) tan x
D) cot x
E) ln(cos x)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
Differentiate the function y = 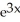 ln(3x).
ln(3x).
A) 3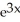 ln(3x) +
ln(3x) + 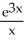
B) 3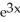 ln(3x) -
ln(3x) - 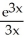
C) 3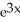 ln(3x) +
ln(3x) + 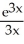
D)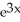 ln(3x) +
ln(3x) + 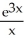
E) none of the above
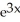 ln(3x).
ln(3x).A) 3
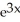 ln(3x) +
ln(3x) + 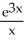
B) 3
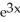 ln(3x) -
ln(3x) - 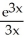
C) 3
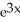 ln(3x) +
ln(3x) + 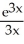
D)
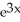 ln(3x) +
ln(3x) + 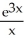
E) none of the above

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
Find an antiderivative of cos(2x) 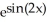 .
.
A) 2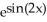 + C
+ C
B)
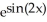 + C
+ C
C)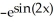 + C
+ C
D) -
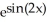 + C
+ C
E) -2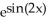 + C
+ C
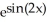 .
.A) 2
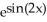 + C
+ CB)

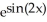 + C
+ CC)
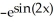 + C
+ CD) -

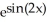 + C
+ CE) -2
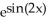 + C
+ C
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
Prove the following: 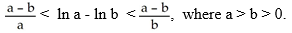
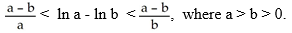

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
The population of a city is growing exponentially, increasing at the rate of 1.6% per year. A new bicycle route must be in place before the population doubles from its current value. How long (rounded up to the nearest year) does the city have before the new bicycle route must be completed?
A) 40 years
B) 55 years
C) 44 years
D) 60 years
E) 50 years
A) 40 years
B) 55 years
C) 44 years
D) 60 years
E) 50 years

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
A population of bacteria grows continuously at a rate of 15% of its current population. If there are 10,000 bacteria present initially, how many (to the nearest 100) will there be after four hours?
A) 17,500
B) 18,200
C) 16,500
D) 15,300
E) 19,100
A) 17,500
B) 18,200
C) 16,500
D) 15,300
E) 19,100

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
When a quantity of sugar is placed in a container of water, the sugar dissolves at a rate proportional to the amount of sugar remaining undissolved. Suppose that 30 g of sugar is placed in 1 L of water and that 5 minutes later the concentration of sugar dissolved in the water is 25 g/L.Find a formula for A(t), the amount of sugar that is dissolved t minutes after the sugar was placed in the water.
A) A(t) = 30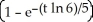 g
g
B) A(t) = 30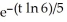 g
g
C) A(t) = 30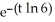 g
g
D) A(t) = 30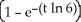 g
g
E) A(t) = 30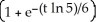 g
g
A) A(t) = 30
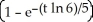 g
gB) A(t) = 30
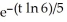 g
gC) A(t) = 30
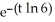 g
gD) A(t) = 30
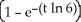 g
gE) A(t) = 30
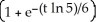 g
g
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
A thermometer reading -7°C is brought into a room kept at 23°C. Half a minute later the thermometer reads 8°C. What is the temperature reading of the thermometer after a further two and a half minutes?
A) 12.5°C
B) 32.5°C
C) 22.5°C
D) 15.5°C
E) 28.5°C
A) 12.5°C
B) 32.5°C
C) 22.5°C
D) 15.5°C
E) 28.5°C

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
The 2000 census recorded a population of 16.1 million in a certain country, while in 2010 the figure was 32.8 million. Assuming that the rate of population growth is proportional to the population, predict the population in the year 2015.
A) 39.8 million
B) 46.8 million
C) 36.8 million
D) 41.8 million
E) 52.8 million
A) 39.8 million
B) 46.8 million
C) 36.8 million
D) 41.8 million
E) 52.8 million

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
A dish with a temperature of 54°C is placed in a fridge, which has a constant temperature of 6°C.If the dish cools to 30°C in a half hour, what is its temperature after another half hour?Assume Newton's Law of Cooling.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
The rate at which a drug is absorbed into the bloodstream is given by 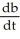 = a -
= a - 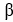 b, where b(t) is the concentration of the drug in the bloodstream at time t minutes after the drug is ingested, and a and b are positive constants. How long does it take for b(t) to rise to half its limiting value as t
b, where b(t) is the concentration of the drug in the bloodstream at time t minutes after the drug is ingested, and a and b are positive constants. How long does it take for b(t) to rise to half its limiting value as t
?
A)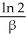 minutes
minutes
B) -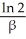 minutes
minutes
C)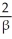 minutes
minutes
D)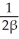 minutes
minutes
E)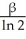 minutes
minutes
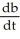 = a -
= a - 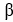 b, where b(t) is the concentration of the drug in the bloodstream at time t minutes after the drug is ingested, and a and b are positive constants. How long does it take for b(t) to rise to half its limiting value as t
b, where b(t) is the concentration of the drug in the bloodstream at time t minutes after the drug is ingested, and a and b are positive constants. How long does it take for b(t) to rise to half its limiting value as t ?
A)
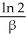 minutes
minutesB) -
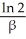 minutes
minutesC)
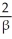 minutes
minutesD)
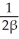 minutes
minutesE)
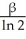 minutes
minutes
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
If a village has a population of 340 people and its population grows continuously at an annual rate of 2.3%, what will the population be in 6 years? (Round your answer to the nearest integer.)
A) 370
B) 381
C) 390
D) 400
E) 412
A) 370
B) 381
C) 390
D) 400
E) 412

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
A certain radioactive isotope has a half-life of 37 years. How many years will it take for 100 grams to decay to 64 grams?
A) 18.17 years
B) 33.54 years
C) 23.82 years
D) 28.71 years
E) 24.89 years
A) 18.17 years
B) 33.54 years
C) 23.82 years
D) 28.71 years
E) 24.89 years

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
A certain radioactive isotope decays from 70 grams to 45 grams in 27 years. What is the half-life of the isotope?
A) 40.16 years
B) 42.36 years
C) 48.31 years
D) 50.02 years
E) 36.25 years
A) 40.16 years
B) 42.36 years
C) 48.31 years
D) 50.02 years
E) 36.25 years

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
A certain radioactive isotope has a half-life of 14 years. If 19 grams of the isotope are left after 5 years, how much was present at the beginning?
A) 27.21 grams
B) 24.34 grams
C) 22.10 grams
D) 26.55 grams
E) 34.75 grams
A) 27.21 grams
B) 24.34 grams
C) 22.10 grams
D) 26.55 grams
E) 34.75 grams

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
An object of temperature 44°C is placed in a freezer which is maintained at a temperature of -16°C. At the end of 10 minutes, the object has cooled to a temperature of 14°C. Assuming Newton's law of cooling, what is the temperature of the object (in degree Celsius) after a long time (that is, as 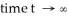 )?
)?
A) -16
B)
C) -
D) 0
E) -67
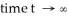 )?
)?A) -16
B)
C) -
D) 0
E) -67

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
The temperature x(t) (in degree Celsius) at time t ( in hours) of an object is given by x(t) = -5 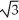 +45
+45 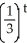 . When will the temperature of the object be 0°C?
. When will the temperature of the object be 0°C?
Express your answer without logarithms.
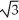 +45
+45  . When will the temperature of the object be 0°C?
. When will the temperature of the object be 0°C?Express your answer without logarithms.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
Find 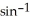 (1/
(1/ 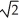 ).
).
A)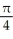
B)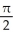
C)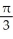
D) -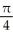
E)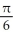
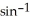 (1/
(1/ 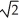 ).
).A)
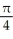
B)
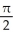
C)
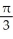
D) -
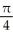
E)
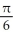

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate 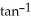
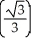 .
.
A)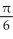
B)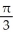
C) -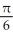
D) -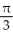
E)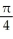
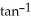
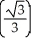 .
.A)
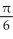
B)
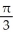
C) -
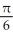
D) -
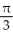
E)
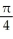

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
Simplify 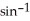 (sin ).
(sin ).
A) 0
B)
C)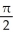
D) -
E) -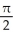
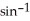 (sin ).
(sin ).A) 0
B)
C)
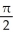
D) -
E) -

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
Simplify cos( 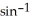 (x)).
(x)).
A)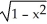
B) -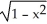
C)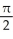
D) 0
E) -sin(x)
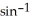 (x)).
(x)).A)
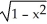
B) -
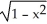
C)
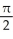
D) 0
E) -sin(x)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck


