Deck 3: Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/131
Play
Full screen (f)
Deck 3: Differentiation
1
Find the slope of the tangent line to the curve y = 4x - 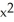 at the point (-1, 0).
at the point (-1, 0).
A) -1
B) 2
C) 6
D)
E) -2
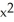 at the point (-1, 0).
at the point (-1, 0).A) -1
B) 2
C) 6
D)

E) -2
6
2
Find the equation of the tangent line to the curve y = 2x - 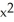 at the point (2, 0).
at the point (2, 0).
A) 2x + y - 4 = 0
B) 2x + y + 4 = 0
C) 2x - y - 4 = 0
D) 2x - y + 4 = 0
E) 2x + y = 0
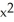 at the point (2, 0).
at the point (2, 0).A) 2x + y - 4 = 0
B) 2x + y + 4 = 0
C) 2x - y - 4 = 0
D) 2x - y + 4 = 0
E) 2x + y = 0
2x + y - 4 = 0
3
Find an equation of the line tangent to the curve y = 2x - 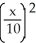 at the point where x = 2.
at the point where x = 2.
A) 25y = 49x - 1
B) 5y = 49x + 1
C) 25y = 49x + 1
D) 25y = 41x + 1
E) 25x = 49y + 1
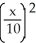 at the point where x = 2.
at the point where x = 2.A) 25y = 49x - 1
B) 5y = 49x + 1
C) 25y = 49x + 1
D) 25y = 41x + 1
E) 25x = 49y + 1
25y = 49x + 1
4
Find an equation of the line tangent to the curve y = 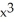 + 1 at the point where x = 2.
+ 1 at the point where x = 2.
A) y = 12x + 15
B) y = 12x -15
C) y = -12x -15
D) y = -12x + 15
E) y = 15x + 12
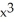 + 1 at the point where x = 2.
+ 1 at the point where x = 2.A) y = 12x + 15
B) y = 12x -15
C) y = -12x -15
D) y = -12x + 15
E) y = 15x + 12

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
5
Find an equation of the line tangent to the curve y = 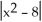 at the point where x = 2.
at the point where x = 2.
A) y = -4x + 12
B) y = 4x - 4
C) y = -4x + 4
D) y = 4x + 4
E) y = 4x - 12
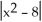 at the point where x = 2.
at the point where x = 2.A) y = -4x + 12
B) y = 4x - 4
C) y = -4x + 4
D) y = 4x + 4
E) y = 4x - 12

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
6
Find an equation of the line tangent to the curve y = 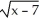 at the point where x = 11.
at the point where x = 11.
A) y = x +
x + 
B) y = x -
x - 
C) y = 4x -
D) y = 4x +
E) y = - x -
x - 
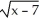 at the point where x = 11.
at the point where x = 11.A) y =
 x +
x + 
B) y =
 x -
x - 
C) y = 4x -

D) y = 4x +

E) y = -
 x -
x - 

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
7
Find an equation of the line tangent to the curve y = 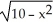 at the point (1, 3).
at the point (1, 3).
A) y = - x +
x + 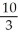
B) y = - x -
x - 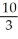
C) y = x +
x + 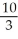
D) y = x -
x - 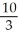
E) y = 3x - 10
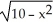 at the point (1, 3).
at the point (1, 3).A) y = -
 x +
x + 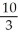
B) y = -
 x -
x - 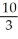
C) y =
 x +
x + 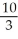
D) y =
 x -
x - 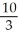
E) y = 3x - 10

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
8
Let f(x) be a function such that = 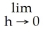
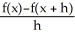
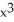 - 1. Find the slope of the line tangent to the graph of f at the point (a, f(a)).
- 1. Find the slope of the line tangent to the graph of f at the point (a, f(a)).
A) 3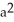
B) 1 -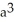
C) -3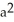
D)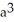 - 1
- 1
E)
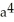 - a + C
- a + C
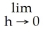
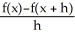
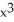 - 1. Find the slope of the line tangent to the graph of f at the point (a, f(a)).
- 1. Find the slope of the line tangent to the graph of f at the point (a, f(a)).A) 3
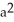
B) 1 -
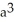
C) -3
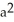
D)
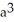 - 1
- 1E)

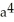 - a + C
- a + C
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
9
Find the point(s) on the curve y = 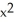 such that the tangent lines to the curve at those points pass through (2, -12).
such that the tangent lines to the curve at those points pass through (2, -12).
A) (6, 36) and (-2, 4)
B) (6, 36) and (2, 4)
C) (-6, 36) and (-2, 4)
D) (-6, 6) and (-2, 4)
E) (6, -36) and (-2, 4)
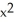 such that the tangent lines to the curve at those points pass through (2, -12).
such that the tangent lines to the curve at those points pass through (2, -12).A) (6, 36) and (-2, 4)
B) (6, 36) and (2, 4)
C) (-6, 36) and (-2, 4)
D) (-6, 6) and (-2, 4)
E) (6, -36) and (-2, 4)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
10
Find the standard equation of the circle with centre at (1, 3) which is tangent to the line 5x - 12y = 8.
A)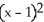 -
- 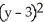 = 1
= 1
B)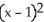 +
+ 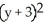 = 9
= 9
C)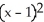 +
+ 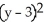 = 9
= 9
D)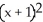 +
+ 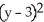 = 8
= 8
E)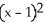 +
+ 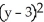 = 8
= 8
A)
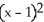 -
- 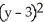 = 1
= 1B)
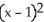 +
+ 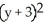 = 9
= 9C)
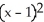 +
+ 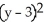 = 9
= 9D)
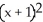 +
+ 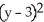 = 8
= 8E)
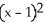 +
+ 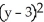 = 8
= 8
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
11
If the line 4x - 9y = 0 is tangent in the first quadrant to the graph of y = 
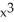 + c, what is the value of c?
+ c, what is the value of c?
A) -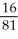
B)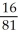
C)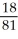
D)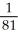
E)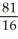

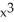 + c, what is the value of c?
+ c, what is the value of c?A) -
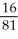
B)
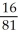
C)
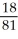
D)
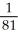
E)
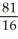

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
12
Using the definition of the derivative, find the derivative of f(x) = 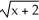 .
.
A)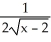
B)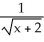
C)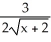
D)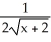
E)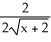
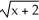 .
.A)
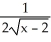
B)
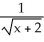
C)
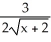
D)
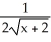
E)
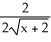

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
13
Find the derivative  (x) of the function f(x) =
(x) of the function f(x) = 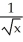 .
.
A) -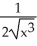
B)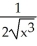
C) -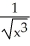
D) -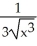
E)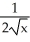
 (x) of the function f(x) =
(x) of the function f(x) = 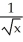 .
.A) -
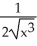
B)
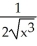
C) -
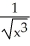
D) -
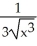
E)
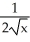

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
14
Find the tangent line to the curve y = 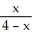 at the origin.
at the origin.
A) y = - x
x
B) y = x
C) y = x
x
D) y = - x
x
E) y = x
x
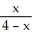 at the origin.
at the origin.A) y = -
 x
xB) y = x
C) y =
 x
xD) y = -
 x
xE) y =
 x
x
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
15
Where is the function f(x) = 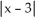 differentiable?
differentiable?
A) at every x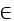 (- , )
(- , )
B) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 0) 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (0, )
C) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 3)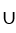 (3, )
(3, )
D) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 0) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (0, 3) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (3, )
E) none of the above
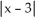 differentiable?
differentiable?A) at every x
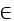 (- , )
(- , )B) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 0) 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (0, )
C) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 3)
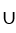 (3, )
(3, )D) at every x 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , 0) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (0, 3) 11ee7b09_453f_4329_ae82_2b7669cf7fd7_TB9661_11 (3, )
E) none of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
16
Find the equation of the straight line that passes through the point P(0,- 3) and is tangent to the curve 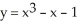 .
.
A) y = -3
B) y = 2x - 3
C) y = -3x
D) y = -x - 3
E) y = x - 3
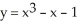 .
.A) y = -3
B) y = 2x - 3
C) y = -3x
D) y = -x - 3
E) y = x - 3

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
17
If f(x) =  (
( 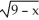 ), calculate f'(5) by using the definition of the derivative.
), calculate f'(5) by using the definition of the derivative.
A)
B) -
C) -
D) -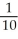
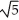
E)
 (
( 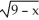 ), calculate f'(5) by using the definition of the derivative.
), calculate f'(5) by using the definition of the derivative.A)

B) -

C) -

D) -
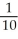
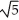
E)


Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
18
Find the slope of the line tangent to the curve 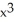 y = 1 at the point
y = 1 at the point 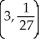 .
.
A)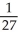
B) -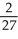
C) -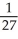
D)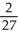
E)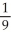
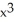 y = 1 at the point
y = 1 at the point 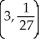 .
.A)
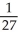
B) -
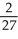
C) -
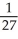
D)
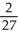
E)
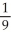

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
19
If f(x) = 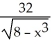 , calculate f'(-2) directly from the definition of the derivative.
, calculate f'(-2) directly from the definition of the derivative.
A) 3
B) 3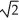
C) -3
D) 4
E) 2
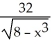 , calculate f'(-2) directly from the definition of the derivative.
, calculate f'(-2) directly from the definition of the derivative.A) 3
B) 3
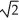
C) -3
D) 4
E) 2

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
20
Let g(x) be a function such that 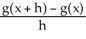 = -
= - 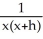 . Find
. Find 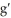 (x).
(x).
A)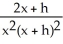
B) -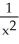
C) -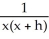
D)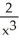
E)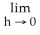
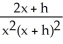
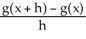 = -
= - 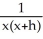 . Find
. Find 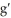 (x).
(x).A)
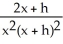
B) -
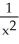
C) -
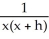
D)
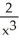
E)
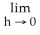
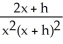

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
21
Calculate the derivative of g(t) = 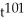 +
+ 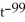 using the general power rule.
using the general power rule.
A) 101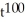 - 99
- 99 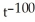
B) 101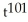 - 99
- 99 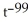
C) -101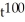 - 99
- 99 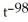
D) 100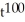 - 98
- 98 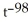
E) 101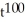 + 99
+ 99 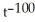
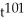 +
+ 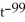 using the general power rule.
using the general power rule.A) 101
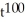 - 99
- 99 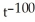
B) 101
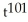 - 99
- 99 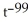
C) -101
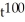 - 99
- 99 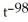
D) 100
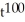 - 98
- 98 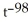
E) 101
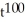 + 99
+ 99 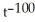

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
22
If f(x) is an even, differentiable function, then  (x)
(x)
A) is an odd function.
B) is an even function.
C) is neither odd nor even.
D) may be either even or odd or neither.
 (x)
(x)A) is an odd function.
B) is an even function.
C) is neither odd nor even.
D) may be either even or odd or neither.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
23
If the curve y = f(x) has a tangent line at (a, f(a)), then f is differentiable at x = a.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
24
If = 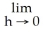
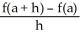 - , then the graph of f has a tangent line at x = a.
- , then the graph of f has a tangent line at x = a.
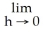
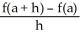 - , then the graph of f has a tangent line at x = a.
- , then the graph of f has a tangent line at x = a. 
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
25
If f is continuous at x = a, then f is differentiable at x = a.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
26
If 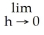
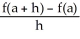 exists, then f is continuous at x = a.
exists, then f is continuous at x = a.
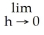
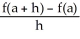 exists, then f is continuous at x = a.
exists, then f is continuous at x = a.
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
27
The domain of the derivative of a function is the same as the domain of the function.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
28
Differentiate f(x) = 10 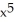 .
.
A) 10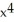
B) 50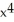
C) 55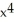
D) 50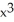
E) 50x
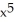 .
.A) 10
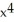
B) 50
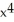
C) 55
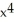
D) 50
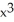
E) 50x

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
29
Find 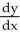 if y = 4
if y = 4 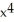 + 3
+ 3 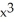 + x - 6.
+ x - 6.
A) 16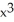 - 9
- 9 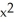 + 1
+ 1
B) 16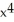 + 9
+ 9 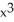 + 1
+ 1
C) 16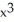 + 9
+ 9 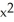 + 1
+ 1
D) 16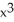 + 9
+ 9 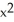 - 6
- 6
E) 16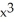 + 9
+ 9 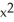 - 5
- 5
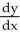 if y = 4
if y = 4 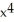 + 3
+ 3 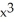 + x - 6.
+ x - 6.A) 16
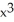 - 9
- 9 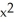 + 1
+ 1B) 16
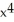 + 9
+ 9 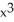 + 1
+ 1C) 16
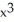 + 9
+ 9 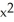 + 1
+ 1D) 16
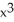 + 9
+ 9 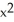 - 6
- 6E) 16
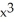 + 9
+ 9 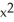 - 5
- 5
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
30
Differentiate the function f(x) = (2 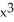 + 5)(3
+ 5)(3 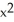 - x).
- x).
A) 30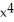 - 8
- 8 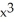 + 30x - 5
+ 30x - 5
B) 30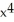 - 8
- 8 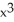 + 30x + 5
+ 30x + 5
C) 30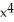 + 8
+ 8 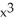 + 30x - 5
+ 30x - 5
D) 30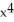 + 8
+ 8 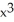 - 30x - 5
- 30x - 5
E) 36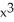 - 6
- 6 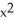
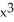 + 5)(3
+ 5)(3 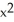 - x).
- x).A) 30
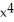 - 8
- 8 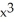 + 30x - 5
+ 30x - 5B) 30
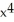 - 8
- 8 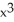 + 30x + 5
+ 30x + 5C) 30
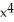 + 8
+ 8 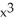 + 30x - 5
+ 30x - 5D) 30
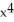 + 8
+ 8 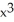 - 30x - 5
- 30x - 5E) 36
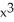 - 6
- 6 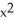

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
31
Find the equation of the tangent line to the curve y = (2 - 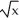 )(1 +
)(1 + 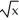 + 3x) at the point (1, 5).
+ 3x) at the point (1, 5).
A) x - y + 4 = 0
B) x + y - 6 = 0
C) x - y - 4 = 0
D) 6x - y - 1 = 0
E) x + y + 4 = 0
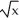 )(1 +
)(1 + 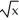 + 3x) at the point (1, 5).
+ 3x) at the point (1, 5).A) x - y + 4 = 0
B) x + y - 6 = 0
C) x - y - 4 = 0
D) 6x - y - 1 = 0
E) x + y + 4 = 0

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
32
Find the points on the curve y = 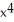 - 6
- 6 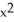 + 4 where the tangent line is horizontal.
+ 4 where the tangent line is horizontal.
A) (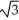 , -5) and (-
, -5) and (- 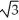 , -5)
, -5)
B) (0, 4), (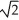 , -5), and (-
, -5), and (- 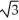 , -5)
, -5)
C) (0, 4), (-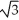 , 5), and (
, 5), and ( 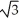 , -5)
, -5)
D) (0, 4), (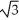 , -5), and (-
, -5), and (- 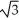 , -5)
, -5)
E) (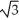 , 5) and (-
, 5) and (- 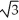 , 5)
, 5)
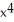 - 6
- 6 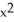 + 4 where the tangent line is horizontal.
+ 4 where the tangent line is horizontal.A) (
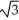 , -5) and (-
, -5) and (- 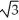 , -5)
, -5)B) (0, 4), (
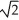 , -5), and (-
, -5), and (- 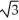 , -5)
, -5)C) (0, 4), (-
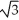 , 5), and (
, 5), and ( 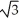 , -5)
, -5)D) (0, 4), (
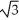 , -5), and (-
, -5), and (- 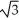 , -5)
, -5)E) (
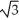 , 5) and (-
, 5) and (- 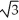 , 5)
, 5)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
33
Given g(x) = 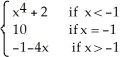 which of the following statements is true?
which of the following statements is true?
A) g is differentiable at x = -1
B) g is not differentiable at x = -1
C)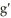 (-1) = -4
(-1) = -4
D) g is continuous at x = -1
E) g is continuous from the left at x = -1
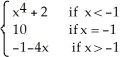 which of the following statements is true?
which of the following statements is true?A) g is differentiable at x = -1
B) g is not differentiable at x = -1
C)
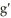 (-1) = -4
(-1) = -4D) g is continuous at x = -1
E) g is continuous from the left at x = -1

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
34
Lines passing through the point (0, 2) are tangent to the graph of y = - 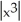 . Find the points of tangency.
. Find the points of tangency.
A) (1, -1) and (-1, 1)
B) (2, -8) and (-2, -8)
C) (1, -1) and (-2, -8)
D) (2, -8) and (-1, 1)
E) (1, 1) and (-1, -1)
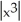 . Find the points of tangency.
. Find the points of tangency.A) (1, -1) and (-1, 1)
B) (2, -8) and (-2, -8)
C) (1, -1) and (-2, -8)
D) (2, -8) and (-1, 1)
E) (1, 1) and (-1, -1)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
35
Where does the normal line to the curve y = x - 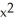 at the point (1, 0) intersect the curve a second time?
at the point (1, 0) intersect the curve a second time?
A) (-2, -6)
B) (- , -
, -  )
)
C) (-1, -2)
D) (0, 0)
E) It does not intersect the curve a second time.
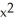 at the point (1, 0) intersect the curve a second time?
at the point (1, 0) intersect the curve a second time?A) (-2, -6)
B) (-
 , -
, -  )
)C) (-1, -2)
D) (0, 0)
E) It does not intersect the curve a second time.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following statements is always true?
A) If f is continuous at c, then it must be differentiable at c.
B) If f is differentiable at c, then it must be continuous at c.
C) If f is not differentiable at c, then it must be discontinuous at c.
D) If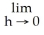 f(c + h) = f(c), then f must be differentiable at c.
f(c + h) = f(c), then f must be differentiable at c.
E) All of the above
A) If f is continuous at c, then it must be differentiable at c.
B) If f is differentiable at c, then it must be continuous at c.
C) If f is not differentiable at c, then it must be discontinuous at c.
D) If
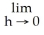 f(c + h) = f(c), then f must be differentiable at c.
f(c + h) = f(c), then f must be differentiable at c.E) All of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
37
How many tangent lines to the graph of y = 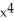 -15
-15 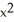 - 10 pass through the point (0, 2)?
- 10 pass through the point (0, 2)?
A) 0
B) 1
C) 2
D) 3
E) 4
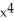 -15
-15 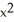 - 10 pass through the point (0, 2)?
- 10 pass through the point (0, 2)?A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
38
Let f(x) = 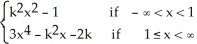 .Find all values of the real number k so that f is differentiable at x = 1.
.Find all values of the real number k so that f is differentiable at x = 1.
A) -2 and 1
B) 2 and -1
C) -2 and 2
D) only -2
E) only 2
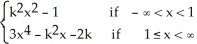 .Find all values of the real number k so that f is differentiable at x = 1.
.Find all values of the real number k so that f is differentiable at x = 1.A) -2 and 1
B) 2 and -1
C) -2 and 2
D) only -2
E) only 2

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
39
There are lines that pass through the point (-1, 3) and are tangent to the curve xy = 1. Find all their slopes.
A) -1 and -9
B) -1 and 9
C) 1 and 9
D) 1 and -9
E) none of the above
A) -1 and -9
B) -1 and 9
C) 1 and 9
D) 1 and -9
E) none of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
40
Find the derivative of 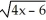 .
.
A)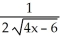
B)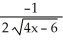
C)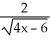
D)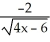
E)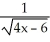
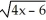 .
.A)
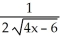
B)
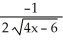
C)
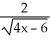
D)
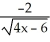
E)
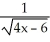

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
41
Find the derivative of f(x) = 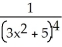 .
.
A) -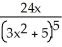
B)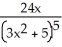
C)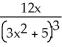
D) -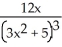
E) -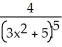
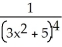 .
.A) -
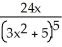
B)
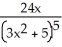
C)
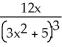
D) -
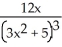
E) -
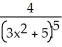

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
42
Differentiate the following function: f(x) = 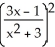 .
.
A)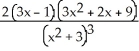
B)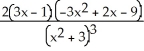
C)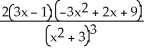
D)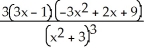
E) none of the above
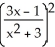 .
.A)
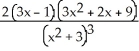
B)
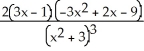
C)
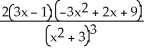
D)
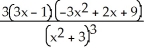
E) none of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
43
Differentiate the following function: f(x) = 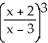 .
.
A) 14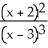
B) -15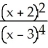
C) -16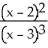
D) 17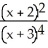
E) 3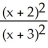
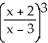 .
.A) 14
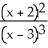
B) -15
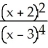
C) -16
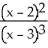
D) 17
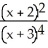
E) 3
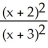

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
44
Find an equation of the line tangent to the curve y = 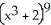 at the point (-1, 1).
at the point (-1, 1).
A) 27x - y + 28 = 0
B) 27x + y + 26 = 0
C) 27y - x - 28 = 0
D) 27y + x - 26 = 0
E) 9x - y + 10 = 0
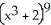 at the point (-1, 1).
at the point (-1, 1).A) 27x - y + 28 = 0
B) 27x + y + 26 = 0
C) 27y - x - 28 = 0
D) 27y + x - 26 = 0
E) 9x - y + 10 = 0

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
45
Use the values in the table below to evaluate  (-2)
(-2)
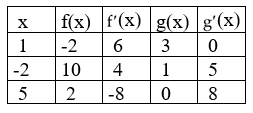
 (-2)
(-2)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
46
Assuming all indicated derivatives exist, ( 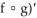 (c) is equal to
(c) is equal to
A) (g(c))
(g(c)) 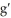 (c)
(c)
B) (c) g(c) + f(c)
(c) g(c) + f(c) 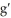 (c)
(c)
C) (c)
(c) 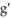 (c)
(c)
D) (c)
(c)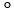
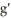 (c)
(c)
E) (
( 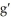 (c))
(c))
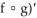 (c) is equal to
(c) is equal toA)
 (g(c))
(g(c)) 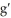 (c)
(c)B)
 (c) g(c) + f(c)
(c) g(c) + f(c) 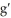 (c)
(c)C)
 (c)
(c) 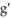 (c)
(c)D)
 (c)
(c)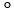
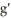 (c)
(c)E)
 (
( 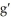 (c))
(c))
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
47
Let f(x) = (x - 2)( 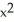 + 4x - 7). Find all the points on this curve where the tangent line is horizontal.
+ 4x - 7). Find all the points on this curve where the tangent line is horizontal.
A)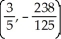 and
and 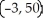
B)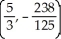 and
and 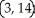
C)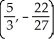 and
and 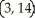
D)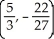 and
and 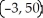
E)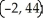
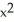 + 4x - 7). Find all the points on this curve where the tangent line is horizontal.
+ 4x - 7). Find all the points on this curve where the tangent line is horizontal.A)
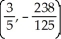 and
and 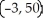
B)
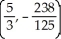 and
and 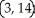
C)
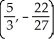 and
and 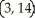
D)
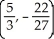 and
and 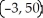
E)
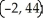

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
48
Find 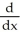
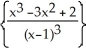 . Simplify your answer.
. Simplify your answer.
A)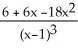
B)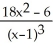
C)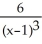
D) -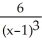
E)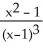
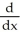
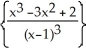 . Simplify your answer.
. Simplify your answer.A)
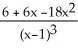
B)
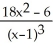
C)
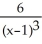
D) -
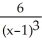
E)
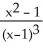

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
49
Where does the function f(x) = 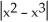 fail to be differentiable?
fail to be differentiable?
A) f(x) is differentiable everywhere.
B) at x = 0
C) at x = 1
D) at x = 0 and x = 1
E) none of the above
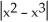 fail to be differentiable?
fail to be differentiable?A) f(x) is differentiable everywhere.
B) at x = 0
C) at x = 1
D) at x = 0 and x = 1
E) none of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
50
The function f(x) = 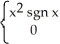
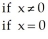 is differentiable at x = 0.
is differentiable at x = 0.
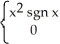
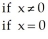 is differentiable at x = 0.
is differentiable at x = 0.
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
51
Differentiate y = sin 4x.
A) 2cos 4x
B) 4cos 2x
C) -4cos 4x
D) 4cos 4x
E) cos 4x
A) 2cos 4x
B) 4cos 2x
C) -4cos 4x
D) 4cos 4x
E) cos 4x

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
52
Find the derivative of y = tan(cos( 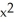 )).
)).
A)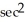 (-sin(2x))
(-sin(2x))
B) 2x cos(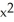 )
)
C)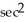 (-2x sin(
(-2x sin( 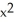 ))
))
D)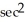 (
( 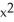 ) cos(
) cos( 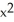 ) - tan(
) - tan( 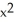 ) sin(
) sin( 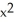 )
)
E) -2x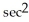 (cos(
(cos( 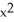 )) sin(
)) sin( 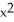 )
)
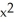 )).
)).A)
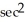 (-sin(2x))
(-sin(2x))B) 2x cos(
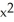 )
)C)
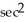 (-2x sin(
(-2x sin( 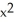 ))
))D)
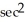 (
( 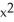 ) cos(
) cos( 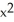 ) - tan(
) - tan( 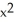 ) sin(
) sin( 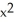 )
)E) -2x
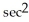 (cos(
(cos( 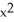 )) sin(
)) sin( 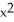 )
)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
53
Find the derivative of f(t) = 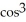 (5t).
(5t).
A) 15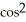 (5t) sin(5t)
(5t) sin(5t)
B) -3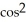 (5t) sin(5t)
(5t) sin(5t)
C) -15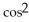 (5t) sin(5t)
(5t) sin(5t)
D) 15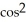 (5t)
(5t)
E) 3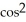 (5t)
(5t)
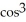 (5t).
(5t).A) 15
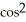 (5t) sin(5t)
(5t) sin(5t)B) -3
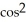 (5t) sin(5t)
(5t) sin(5t)C) -15
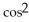 (5t) sin(5t)
(5t) sin(5t)D) 15
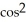 (5t)
(5t)E) 3
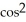 (5t)
(5t)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
54
Differentiate 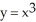 sin 2x.
sin 2x.
A)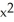 sin 2x +
sin 2x + 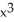 cos 2x
cos 2x
B)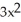 sin 2x +
sin 2x + 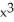 cos 2x
cos 2x
C) 3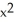 sin 2x - 2
sin 2x - 2 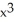 cos 2x
cos 2x
D)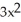 sin 2x + 2
sin 2x + 2 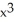 cos 2x
cos 2x
E) 3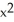 cos(2x)
cos(2x)
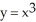 sin 2x.
sin 2x.A)
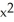 sin 2x +
sin 2x + 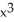 cos 2x
cos 2xB)
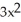 sin 2x +
sin 2x + 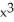 cos 2x
cos 2xC) 3
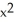 sin 2x - 2
sin 2x - 2 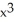 cos 2x
cos 2xD)
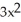 sin 2x + 2
sin 2x + 2 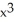 cos 2x
cos 2xE) 3
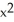 cos(2x)
cos(2x)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
55
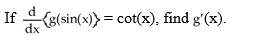

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
56
Find the derivative of y = tan( 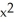 ).
).
A) x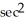 (
( 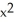 )
)
B) 4x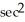
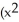 )
)
C) 2x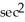
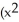 )
)
D) 2x sec(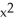 ) tan(
) tan( 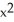 )
)
E)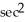 (
( 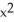 )
)
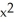 ).
).A) x
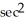 (
( 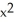 )
)B) 4x
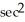
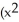 )
)C) 2x
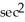
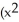 )
)D) 2x sec(
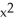 ) tan(
) tan( 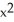 )
)E)
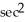 (
( 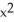 )
)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
57
Find the derivative of the following function: y = 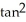 (cos x).
(cos x).
A) -2sin x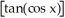
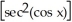
B) 2sin x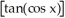
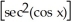
C) -2sin x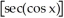
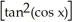
D) -2sin x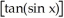
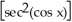
E) -2tan(x)cos(x)sin(x)
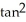 (cos x).
(cos x).A) -2sin x
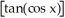
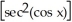
B) 2sin x
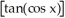
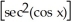
C) -2sin x
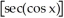
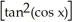
D) -2sin x
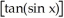
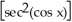
E) -2tan(x)cos(x)sin(x)

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
58
Let y = 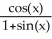 . A simplified expression for
. A simplified expression for 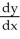 is given by
is given by
A)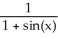
B)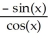
C) -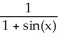
D) - sin(x) - (x)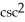
E)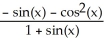
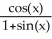 . A simplified expression for
. A simplified expression for 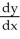 is given by
is given byA)
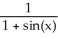
B)
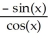
C) -
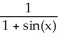
D) - sin(x) - (x)
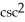
E)
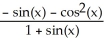

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
59
Find the slope of the curve y = cos 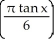 at the point where x =
at the point where x = 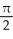 .
.
A) -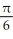
B) -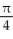
C) -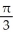
D) -
E) The slope is not defined at x = .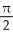
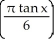 at the point where x =
at the point where x = 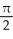 .
.A) -
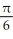
B) -
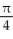
C) -
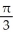
D) -

E) The slope is not defined at x = .
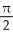

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
60
Find all points in the interval [0,
] where the curve y = 2![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e05_a0f8_cfbe5746361b_TB9661_11.jpg) x - sin(2x) has a horizontal tangent line.
x - sin(2x) has a horizontal tangent line.
A)![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e06_a0f8_5944047c66b9_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e07_a0f8_25dea05cf000_TB9661_11.jpg)
B)![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e08_a0f8_3ba6e7e1af69_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e09_a0f8_1f4f4c0ebbcc_TB9661_11.jpg)
C)![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351a_a0f8_15f81913c98d_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351b_a0f8_25fc087db982_TB9661_11.jpg)
D)![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351c_a0f8_9becefc6ace8_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351d_a0f8_8b110ae34217_TB9661_11.jpg)
E) The tangent line is never horizontal.
] where the curve y = 2
![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e05_a0f8_cfbe5746361b_TB9661_11.jpg) x - sin(2x) has a horizontal tangent line.
x - sin(2x) has a horizontal tangent line.A)
![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e06_a0f8_5944047c66b9_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e07_a0f8_25dea05cf000_TB9661_11.jpg)
B)
![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e08_a0f8_3ba6e7e1af69_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_0e09_a0f8_1f4f4c0ebbcc_TB9661_11.jpg)
C)
![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351a_a0f8_15f81913c98d_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351b_a0f8_25fc087db982_TB9661_11.jpg)
D)
![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351c_a0f8_9becefc6ace8_TB9661_11.jpg) and
and ![<strong>Find all points in the interval [0, \pi ] where the curve y = 2 x - sin(2x) has a horizontal tangent line.</strong> A) and B) and C) and D) and E) The tangent line is never horizontal.](https://storage.examlex.com/TB9661/11ee77e1_784a_351d_a0f8_8b110ae34217_TB9661_11.jpg)
E) The tangent line is never horizontal.

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
61
Find 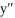 if y =
if y = 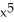 .
.
A) 12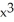
B) 5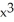
C) 15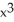
D) 20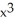
E) 10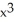
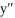 if y =
if y = 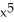 .
.A) 12
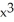
B) 5
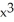
C) 15
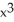
D) 20
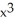
E) 10
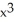

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
62
Find the second derivative of g(x) = 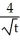 .
.
A)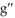 (t) = 2
(t) = 2 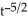
B)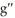 (t) = - 3
(t) = - 3 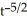
C)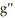 (t) = 3
(t) = 3 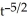
D)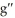 (t) = -2
(t) = -2 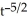
E)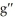 (t) = 4
(t) = 4 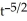
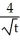 .
.A)
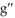 (t) = 2
(t) = 2 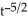
B)
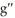 (t) = - 3
(t) = - 3 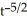
C)
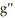 (t) = 3
(t) = 3 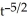
D)
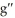 (t) = -2
(t) = -2 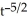
E)
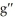 (t) = 4
(t) = 4 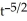

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
63

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
64
Find 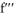 (2) given that =
(2) given that = 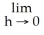 .
. 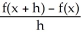
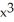 - 7
- 7
A) 12
B) 0
C) 6
D) 5
E) 10
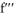 (2) given that =
(2) given that = 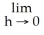 .
. 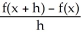
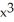 - 7
- 7A) 12
B) 0
C) 6
D) 5
E) 10

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
65
let y = 
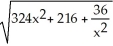 , x > 0. Show that
, x > 0. Show that 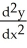 =
= 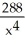 .
.

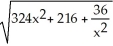 , x > 0. Show that
, x > 0. Show that 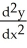 =
= 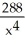 .
.
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
66
Calculate the third derivative of f(x) = 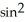 x.
x.
A) -2sin(2x)
B) -4sin(2x)
C) -2cos(2x)
D) -4sin x
E) -2(x)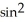
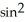 x.
x.A) -2sin(2x)
B) -4sin(2x)
C) -2cos(2x)
D) -4sin x
E) -2(x)
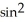

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
67
Find a formula for the nth derivative 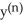 of the function y =
of the function y = 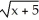 .
.
A)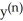 =
= 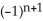
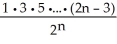
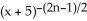
B)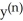 = -
= - 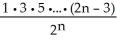
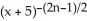
C)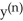 =
= 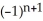
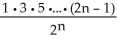
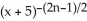
D)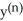 =
= 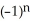
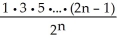
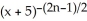
E)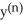 =
= 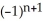
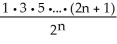
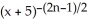
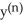 of the function y =
of the function y = 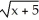 .
.A)
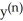 =
= 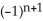
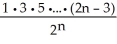
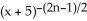
B)
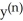 = -
= - 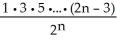
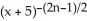
C)
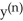 =
= 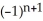
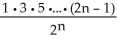
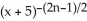
D)
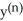 =
= 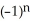
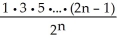
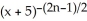
E)
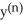 =
= 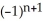
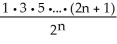
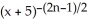

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
68
Find the second derivative of the function f(x) = 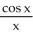 .
.
A) -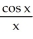 +
+ 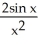 +
+ 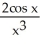
B) -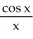 -
- 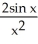 +
+ 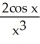
C) -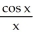 +
+ 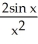 -
- 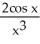
D)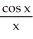 +
+ 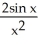 +
+ 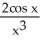
E)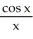 +
+ 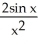 -
- 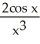
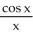 .
.A) -
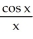 +
+ 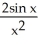 +
+ 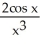
B) -
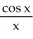 -
- 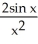 +
+ 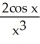
C) -
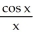 +
+ 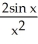 -
- 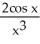
D)
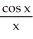 +
+ 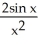 +
+ 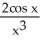
E)
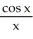 +
+ 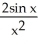 -
- 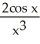

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
69
Find the second derivative of the function f(x) = 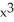 sin(2x).
sin(2x).
A) - 6x sin(2x) + 8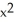 cos(2x) - 4
cos(2x) - 4 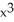 sin(2x)
sin(2x)
B) 6x sin(2x) + 8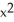 cos(2x) - 4
cos(2x) - 4 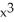 sin(2x)
sin(2x)
C) 6x sin(2x) + 12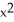 cos(2x) - 4
cos(2x) - 4 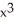 sin(2x)
sin(2x)
D) - 6x sin(2x) + 12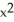 cos(2x) + 4
cos(2x) + 4 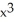 sin(2x)
sin(2x)
E) 6x sin(2x) + 12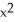 cos(2x) + 4
cos(2x) + 4 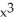 sin(2x)
sin(2x)
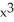 sin(2x).
sin(2x).A) - 6x sin(2x) + 8
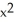 cos(2x) - 4
cos(2x) - 4 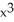 sin(2x)
sin(2x)B) 6x sin(2x) + 8
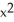 cos(2x) - 4
cos(2x) - 4 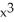 sin(2x)
sin(2x)C) 6x sin(2x) + 12
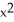 cos(2x) - 4
cos(2x) - 4 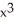 sin(2x)
sin(2x)D) - 6x sin(2x) + 12
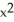 cos(2x) + 4
cos(2x) + 4 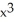 sin(2x)
sin(2x)E) 6x sin(2x) + 12
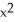 cos(2x) + 4
cos(2x) + 4 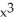 sin(2x)
sin(2x)
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
70
Find the second derivative of the function f(x) = 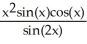 .
.
A) 1
B) x
C) -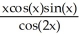
D) -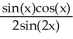
E) 0
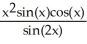 .
.A) 1
B) x
C) -
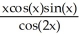
D) -
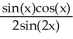
E) 0

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
71
A spherical balloon is being inflated. Find the rate of change of volume with respect to the radius when the radius is 5 cm.
A) 200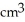 /cm
/cm
B) 100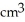 /cm
/cm
C) 300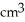 /cm
/cm
D) 400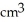 /cm
/cm
E) 500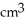 /cm
/cm
A) 200
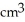 /cm
/cmB) 100
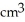 /cm
/cmC) 300
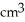 /cm
/cmD) 400
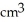 /cm
/cmE) 500
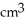 /cm
/cm
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
72
Find the rate of change of the volume of a cube with respect to its edge length x when x = 4 m.
A) 40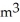 /m
/m
B) 42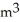 /m
/m
C) 48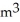 /m
/m
D) 50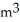 /m
/m
E) 8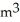 /m
/m
A) 40
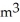 /m
/mB) 42
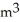 /m
/mC) 48
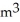 /m
/mD) 50
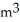 /m
/mE) 8
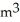 /m
/m
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
73
A spherical balloon is being inflated. Find the rate of increase of the surface area (S = 4 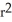 ) with respect to the radius when r = 2 m.
) with respect to the radius when r = 2 m.
A) 16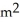 /m
/m
B) 8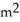 /m
/m
C) 12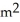 /m
/m
D) 24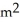 /m
/m
E) 4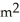 /m
/m
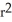 ) with respect to the radius when r = 2 m.
) with respect to the radius when r = 2 m.A) 16
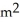 /m
/mB) 8
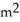 /m
/mC) 12
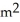 /m
/mD) 24
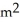 /m
/mE) 4
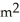 /m
/m
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
74
Find the rate of change of the area of a circle with respect to its circumference C.
A)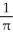 C
C
B)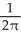 C
C
C)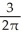 C
C
D)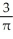 C
C
E)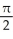 C
C
A)
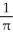 C
CB)
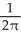 C
CC)
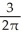 C
CD)
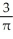 C
CE)
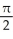 C
C
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
75
The electrical resistance R of a wire of unit length and cross-sectional radius x is given by R = 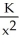 , where K is a non-zero constant real number. By approximately what percentage does the resistance R change if the diameter of the wire is decreased by 6%?
, where K is a non-zero constant real number. By approximately what percentage does the resistance R change if the diameter of the wire is decreased by 6%?
A) -6%
B) -9%
C) 12%
D) 6%
E) -12%
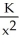 , where K is a non-zero constant real number. By approximately what percentage does the resistance R change if the diameter of the wire is decreased by 6%?
, where K is a non-zero constant real number. By approximately what percentage does the resistance R change if the diameter of the wire is decreased by 6%?A) -6%
B) -9%
C) 12%
D) 6%
E) -12%

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
76
The cost in dollars for a company to produce x pairs of shoes is 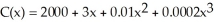 . Find the marginal cost function.
. Find the marginal cost function.
A)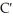 (x) = 1 + 0.02x + 0.0006
(x) = 1 + 0.02x + 0.0006 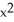
B)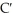 (x) = 1 + 0.01x + 0.0002
(x) = 1 + 0.01x + 0.0002 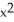
C)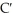 (x) = 3 + 0.02x + 0.0003
(x) = 3 + 0.02x + 0.0003 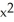
D)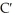 (x) = 3 + 0.02x + 0.0006
(x) = 3 + 0.02x + 0.0006 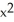
E)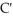 (x) = 3 + 0.01x + 0.0006
(x) = 3 + 0.01x + 0.0006 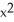
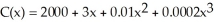 . Find the marginal cost function.
. Find the marginal cost function.A)
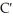 (x) = 1 + 0.02x + 0.0006
(x) = 1 + 0.02x + 0.0006 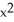
B)
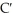 (x) = 1 + 0.01x + 0.0002
(x) = 1 + 0.01x + 0.0002 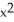
C)
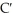 (x) = 3 + 0.02x + 0.0003
(x) = 3 + 0.02x + 0.0003 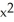
D)
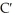 (x) = 3 + 0.02x + 0.0006
(x) = 3 + 0.02x + 0.0006 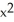
E)
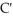 (x) = 3 + 0.01x + 0.0006
(x) = 3 + 0.01x + 0.0006 

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
77
The population (in thousands) of the city of Abbotsford is given by 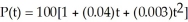 , with t in years and with
, with t in years and with 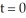 corresponding to 1980. What was the rate of change of P in 1986?
corresponding to 1980. What was the rate of change of P in 1986?
A) 9.6 thousand per year
B) 8.6 thousand per year
C) 7.6 thousand per year
D) 8.9 thousand per year
E) 4.4 thousand per year
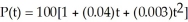 , with t in years and with
, with t in years and with 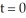 corresponding to 1980. What was the rate of change of P in 1986?
corresponding to 1980. What was the rate of change of P in 1986?A) 9.6 thousand per year
B) 8.6 thousand per year
C) 7.6 thousand per year
D) 8.9 thousand per year
E) 4.4 thousand per year

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
78
The daily cost of production of x widgets in a widget factory is C dollars, where 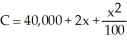 . What is the cost per widget, and what value of x will make the cost per widget as small as possible?
. What is the cost per widget, and what value of x will make the cost per widget as small as possible?
A)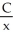 dollars, x = 2,000
dollars, x = 2,000
B)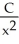 dollars, x = 4,000
dollars, x = 4,000
C)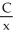 dollars, x = 8,000
dollars, x = 8,000
D)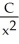 dollars, x = 400
dollars, x = 400
E)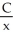 dollars, x = 4,000
dollars, x = 4,000
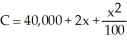 . What is the cost per widget, and what value of x will make the cost per widget as small as possible?
. What is the cost per widget, and what value of x will make the cost per widget as small as possible?A)
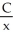 dollars, x = 2,000
dollars, x = 2,000B)
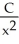 dollars, x = 4,000
dollars, x = 4,000C)
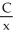 dollars, x = 8,000
dollars, x = 8,000D)
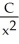 dollars, x = 400
dollars, x = 400E)
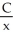 dollars, x = 4,000
dollars, x = 4,000
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
79
If the cost of mining x kg of gold is C(x) = A + Bx + C 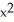 dollars where A, B, and C are positive constants, which of the following statements is true for a given positive value of x?
dollars where A, B, and C are positive constants, which of the following statements is true for a given positive value of x?
A) The marginal cost C'(x) is greater than the cost C(x + 1) - C(x) of mining 1 more kg.
B) The marginal cost C'(x) is less than the cost C(x + 1) - C(x) of mining 1 more kg.
C) The marginal cost C'(x) is equal to the cost C(x + 1) - C(x) of mining 1 more kg.
D) There is not enough information to make any conclusion.
E) None of the above
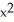 dollars where A, B, and C are positive constants, which of the following statements is true for a given positive value of x?
dollars where A, B, and C are positive constants, which of the following statements is true for a given positive value of x?A) The marginal cost C'(x) is greater than the cost C(x + 1) - C(x) of mining 1 more kg.
B) The marginal cost C'(x) is less than the cost C(x + 1) - C(x) of mining 1 more kg.
C) The marginal cost C'(x) is equal to the cost C(x + 1) - C(x) of mining 1 more kg.
D) There is not enough information to make any conclusion.
E) None of the above

Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck
80
By approximately what percentage does the volume of a cube change if the edge length changes by 1%?
A) 3%
B) 1%
C) 2%
D) 4%
E) %
%
A) 3%
B) 1%
C) 2%
D) 4%
E)
 %
%
Unlock Deck
Unlock for access to all 131 flashcards in this deck.
Unlock Deck
k this deck


