Deck 5: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/91
Play
Full screen (f)
Deck 5: Probability
1
Which of the following probabilities for the sample points A, B, and C could be true if A, B, and C are the only sample points in an experiment?
A) P(A) = 1/ 3, P(B) = 1/ 7, P(C) = 1/ 4
B) P(A) = -1/4, P(B) = 1/2, P(C) = 3/4
C) P(A) = 0, P(B) = 1/ 2, P(C) = 1/ 2
D) P(A) = 1/ 9, P(B) = 1/ 9, P(C) = 1/ 9
A) P(A) = 1/ 3, P(B) = 1/ 7, P(C) = 1/ 4
B) P(A) = -1/4, P(B) = 1/2, P(C) = 3/4
C) P(A) = 0, P(B) = 1/ 2, P(C) = 1/ 2
D) P(A) = 1/ 9, P(B) = 1/ 9, P(C) = 1/ 9
P(A) = 0, P(B) = 1/ 2, P(C) = 1/ 2
2
If A, B, C, and D, are the only possible outcomes of an experiment, find the probability of D using the table below. 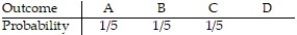 .
.
A) 2/ 5
B) 3/ 5
C) 1/ 5
D) 1/4
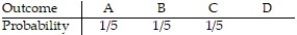 .
.A) 2/ 5
B) 3/ 5
C) 1/ 5
D) 1/4
2/ 5
3
In a 1-pond bag of skittles the possible colors were red, green, yellow, orange, and purple. The probability of drawing a particular color from that bag is given below. Is this a probability model? 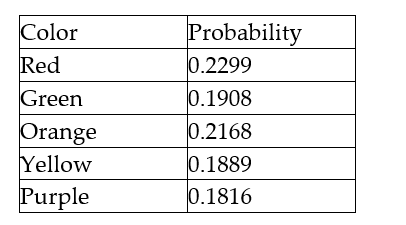

True
4
Which of the following cannot be the probability of an event?
A)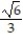
B) 0
C) -72
D) 0.001
A)
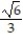
B) 0
C) -72
D) 0.001

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
5
The probability that event A will occur is P(A) = 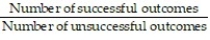
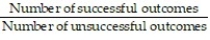

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
6
The probability that event A will occur is P(A) = 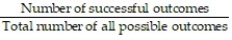
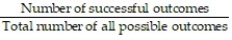

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
7
The table below represents a random sample of the number of deaths per 100 cases for a certain illness over time. If a person infected with this illness is randomly selected from all infected people, find the probability that the person lives 3-4 years after diagnosis. Express your answer as a simplified fraction and as a decimal. 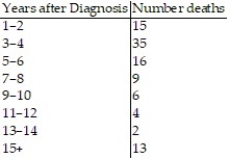
A)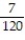 ; 0.058
; 0.058
B)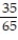 ; 0.538
; 0.538
C)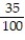 ; 0.35
; 0.35
D)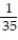 ; 0.029
; 0.029

A)
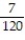 ; 0.058
; 0.058B)
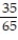 ; 0.538
; 0.538C)
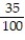 ; 0.35
; 0.35D)
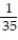 ; 0.029
; 0.029
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
8
You are dealt one card from a standard 52-card deck. Find the probability of being dealt an ace or a 8.
A)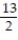
B) 9
C)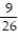
D)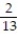
A)
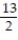
B) 9
C)
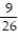
D)
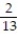

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
9
You are dealt one card from a standard 52-card deck. Find the probability of being dealt a picture card.
A)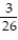
B)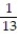
C)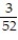
D)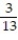
A)
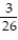
B)
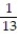
C)
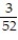
D)
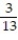

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
10
A fair coin is tossed two times in succession. The set of equally likely outcomes is 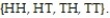 Find the probability of getting the same outcome on each toss.
Find the probability of getting the same outcome on each toss.
A)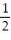
B)
C) 1
D)
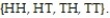 Find the probability of getting the same outcome on each toss.
Find the probability of getting the same outcome on each toss.A)
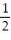
B)

C) 1
D)


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
11
A single die is rolled twice. The set of 36 equally likely outcomes is {(1, 1), (1, 2), (1, 3), (1, 4), 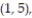
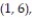
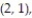
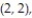 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 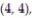
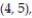
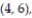
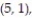
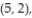 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
-Find the probability of getting two numbers whose sum is greater than 10.
A) 3
B)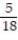
C)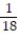
D)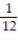
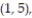
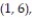
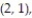
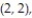 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 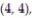
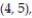
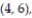
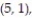
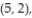 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}. -Find the probability of getting two numbers whose sum is greater than 10.
A) 3
B)
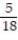
C)
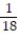
D)
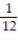

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
12
A single die is rolled twice. The set of 36 equally likely outcomes is {(1, 1), (1, 2), (1, 3), (1, 4), 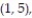
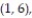
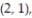
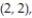 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 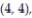
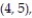
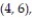
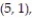
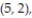 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
-Find the probability of getting two numbers whose sum is less than 13.
A) 0
B) 1
C)
D)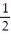
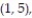
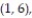
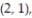
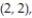 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 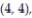
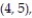
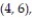
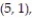
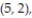 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}. -Find the probability of getting two numbers whose sum is less than 13.
A) 0
B) 1
C)

D)
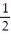

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
13
A single die is rolled twice. The set of 36 equally likely outcomes is {(1, 1), (1, 2), (1, 3), (1, 4), 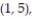
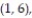
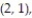
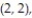 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 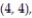
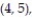
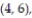
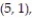
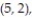 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
- Find the probability of getting two numbers whose sum is greater than 9 and less than 13.
A) 0
B)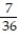
C)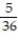
D)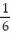
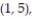
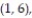
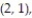
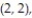 (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), 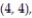
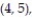
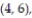
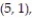
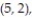 (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
(5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.- Find the probability of getting two numbers whose sum is greater than 9 and less than 13.
A) 0
B)
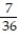
C)
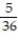
D)
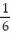

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
14
This problem deals with eye color, an inherited trait. For purposes of this problem, assume that only two eye colors are possible, brown and blue. We use b to represent a blue eye gene and B a brown eye gene. If any B genes are present, the person will have brown eyes. The table shows the four possibilities for the children of two Bb (brown-eyed) parents, where each parent has one of each eye color gene. 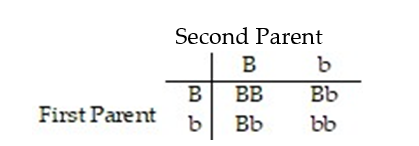 Find the probability that these parents give birth to a child who has blue eyes.
Find the probability that these parents give birth to a child who has blue eyes.
A)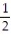
B) 0
C) 1
D)
 Find the probability that these parents give birth to a child who has blue eyes.
Find the probability that these parents give birth to a child who has blue eyes.A)
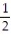
B) 0
C) 1
D)


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
15
The sample space for tossing three fair coins is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. What is the probability of exactly two heads?
A)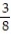
B)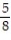
C) 3
D)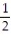
A)
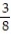
B)
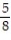
C) 3
D)
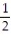

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
16
A probability experiment is conducted in which the sample space of the experiment is 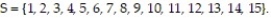 Let event
Let event 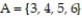 and event
and event 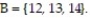 Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
A) { }; no
B) { 3, 4, 5, 6, 12, 13, 14}; yes
C) { 3, 4, 5, 6, 12, 13, 14}; no
D) { }; yes
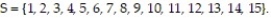 Let event
Let event 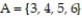 and event
and event 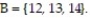 Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?A) { }; no
B) { 3, 4, 5, 6, 12, 13, 14}; yes
C) { 3, 4, 5, 6, 12, 13, 14}; no
D) { }; yes

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
17
The table lists the drinking habits of a group of college students. If a student is chosen at random, find the probability of getting someone who is a regular or heavy drinker. Round your answer to three decimal places. 
A) 0.159
B) 0.264
C) 0.717
D) 0.222

A) 0.159
B) 0.264
C) 0.717
D) 0.222

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
18
The table lists the drinking habits of a group of college students. If a student is chosen at random, find the probability of getting someone who is a man or a woman. Round your answer to three decimal places. 
A) 1
B) 0.916
C) 0.183
D) 0.817

A) 1
B) 0.916
C) 0.183
D) 0.817

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
19
The table lists the drinking habits of a group of college students. If a student is chosen at random, find the probability of getting someone who is a non-drinker. Round your answer to three decimal places. 
A) 0.765
B) 0.235
C) 0.929
D) 1

A) 0.765
B) 0.235
C) 0.929
D) 1

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
20
The distribution of Bachelor's degrees conferred by a university is listed in the table. Assume that a student majors in only one subject. What is the probability that a randomly selected student with a Bachelor's degree majored in Physics or Philosophy? Round your answer to three decimal places. 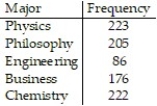
A) 0.531
B) 0.225
C) 0.245
D) 0.469

A) 0.531
B) 0.225
C) 0.245
D) 0.469

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
21
The distribution of Bachelor's degrees conferred by a university is listed in the table. Assume that a student majors in only one subject. What is the probability that a randomly selected student with a Bachelor's degree majored in Business, Chemistry or Engineering? Round your answer to three decimal places. 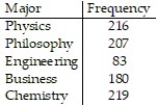
A) 0.533
B) 0.291
C) 0.467
D) 0.334

A) 0.533
B) 0.291
C) 0.467
D) 0.334

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
22
A card is drawn from a standard deck of 52 playing cards. Find the probability that the card is a picture card.
A)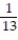
B)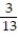
C)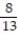
D)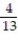
A)
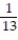
B)
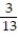
C)
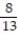
D)
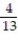

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
23
A probability experiment is conducted in which the sample space of the experiment is 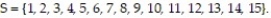 Let event
Let event 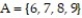 and event
and event 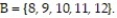 Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
A) { 6, 7, 8, 9, 10, 11, 12}; no
B) { 8, 9}; no
C) { 8, 9}; yes
D) { 6, 7, 8, 9, 10, 11, 12}; yes
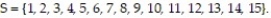 Let event
Let event 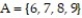 and event
and event 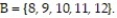 Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?
Assume that each outcome is equally likely. List the outcomes in A and B. Are A and B mutually exclusive?A) { 6, 7, 8, 9, 10, 11, 12}; no
B) { 8, 9}; no
C) { 8, 9}; yes
D) { 6, 7, 8, 9, 10, 11, 12}; yes

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
24
A probability experiment is conducted in which the sample space of the experiment is 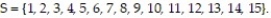 Let event
Let event 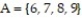 and event B.
and event B. 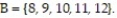 Assume that each outcome is equally likely. List the outcomes in A or B. Find P(A or B).
Assume that each outcome is equally likely. List the outcomes in A or B. Find P(A or B).
A) { 6, 7, 8, 9, 10, 10, 11, 12};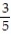
B) { 8, 9};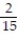
C) { 6, 7, 8, 9, 11, 12};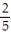
D) { 6, 7, 8, 9, 10, 11, 12};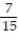
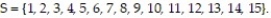 Let event
Let event 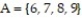 and event B.
and event B. 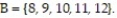 Assume that each outcome is equally likely. List the outcomes in A or B. Find P(A or B).
Assume that each outcome is equally likely. List the outcomes in A or B. Find P(A or B).A) { 6, 7, 8, 9, 10, 10, 11, 12};
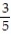
B) { 8, 9};
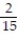
C) { 6, 7, 8, 9, 11, 12};
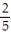
D) { 6, 7, 8, 9, 10, 11, 12};
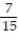

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
25
The events A and B are mutually exclusive. If P(A) = 0.2 and P(B) = 0.5, what is P(A and B) ?
A) 0
B) 0.5
C) 0.1
D) 0.7
A) 0
B) 0.5
C) 0.1
D) 0.7

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
26
Given that P(A or B) = 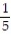 , P(A) =
, P(A) = 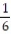 ,and P(A and B )=
,and P(A and B )= 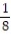 find P(B). Express the probability as a simplified fraction.
find P(B). Express the probability as a simplified fraction.
A)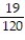
B)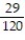
C)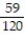
D)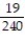
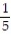 , P(A) =
, P(A) = 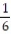 ,and P(A and B )=
,and P(A and B )= 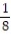 find P(B). Express the probability as a simplified fraction.
find P(B). Express the probability as a simplified fraction.A)
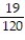
B)
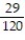
C)
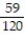
D)
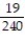

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
27
The table lists the drinking habits of a group of college students. If a student is chosen at random, find the probability of getting someone who is a man or a non-drinker. Round your answer to three decimal places. 
A) 0.949
B) 0.936
C) 0.941
D) 0.793

A) 0.949
B) 0.936
C) 0.941
D) 0.793

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
28
The table lists the drinking habits of a group of college students. If a student is chosen at random, find the probability of getting someone who is a woman or a heavy drinker. Round your answer to three decimal places. 
A) 0.552
B) 0.830
C) 0.915
D) 0.153

A) 0.552
B) 0.830
C) 0.915
D) 0.153

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the data in the table shown which represents the marital status of males and females 18 years or older in the United States in 2003. Determine the probability that a randomly selected U.S. resident 18 years or older is divorced or a male? Round to the nearest hundredth. 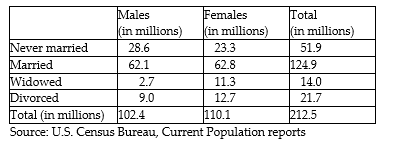
A) 0.58
B) 0.54
C) 0.50
D) 0.04

A) 0.58
B) 0.54
C) 0.50
D) 0.04

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
30
A probability experiment is conducted in which the sample space of the experiment is 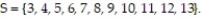 Let event
Let event 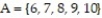 . Assume that each outcome is equally likely. List the outcomes in
. Assume that each outcome is equally likely. List the outcomes in 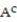 . Find P(
. Find P( 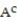 ).
).
A) { 3, 4, 5, 11, 12, 13};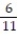
B) { 3, 4, 5, 10, 11, 12, 13};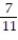
C) { 11, 12, 13};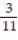
D) { 6, 7, 8, 9, 10};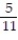
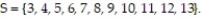 Let event
Let event 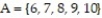 . Assume that each outcome is equally likely. List the outcomes in
. Assume that each outcome is equally likely. List the outcomes in 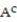 . Find P(
. Find P( 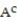 ).
).A) { 3, 4, 5, 11, 12, 13};
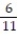
B) { 3, 4, 5, 10, 11, 12, 13};
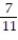
C) { 11, 12, 13};
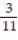
D) { 6, 7, 8, 9, 10};
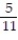

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
31
You are dealt one card from a 52-card deck. Find the probability that you are not dealt a 5. Express the probability as a simplified fraction.
A)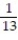
B)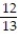
C)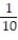
D)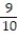
A)
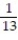
B)
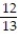
C)
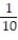
D)
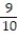

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
32
You are dealt one card from a 52-card deck. Find the probability that you are not dealt a spade. Express the probability as a simplified fraction.
A)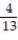
B)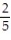
C)
D)
A)
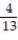
B)
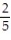
C)

D)


Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
33
The overnight shipping business has skyrocketed in the last ten years. The single greatest predictor of a company's success has been proven time and again to be customer service. A study was conducted to study the customer satisfaction levels for one overnight shipping business. In addition to the customer's satisfaction level, the customers were asked how often they used overnight shipping. The results are shown below in the following table. What is the probability that a respondent did not have a high level of satisfaction with the company? Round the the nearest hundredth. 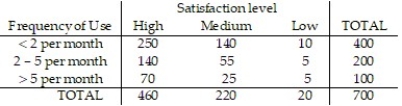
A) 0.43
B) 0.66
C) 0.34
D) 0.57

A) 0.43
B) 0.66
C) 0.34
D) 0.57

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
34
A sample of 285 shoppers at a large suburban mall were asked two questions: (1) Did you see a television ad for the sale at department store X during the past 2 weeks? (2) Did you shop at department store X during the past 2 weeks? The responses to the questions are summarized in the table. What is the probability that a randomly selected shopper from the 285 questioned did not shop at department store X? Round the the nearest thousandth. 
A) 0.281
B) 0.105
C) 0.386
D) 0.614

A) 0.281
B) 0.105
C) 0.386
D) 0.614

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
35
A local country club has a membership of 600 and operates facilities that include an 18-hole championship golf course and 12 tennis courts. Before deciding whether to accept new members, the club president would like to know how many members regularly use each facility. A survey of the membership indicates that 61% regularly use the golf course, 44% regularly use the tennis courts, and 5% use neither of these facilities regularly. What percentage of the 600 use at least one of the golf or tennis facilities?
A) 5%
B) 10%
C) 100%
D) 95%
A) 5%
B) 10%
C) 100%
D) 95%

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
36
P(E) + P(  ) > 1
) > 1
 ) > 1
) > 1
Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
37
A game has three outcomes. The probability of a win is 0.4, the probability of tie is 0.5, and the probability of a loss is 0.1. What is the probability of not winning in a single play of the game.
A) 0.1
B) 0.33
C) 0.6
D) 0.5
A) 0.1
B) 0.33
C) 0.6
D) 0.5

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose that events E and F are independent, P(E) = 0.8 and P(F ) = 0.7. What is the P(E and F )?
A) 0.56
B) 0.056
C) 1.5
D) 0.94
A) 0.56
B) 0.056
C) 1.5
D) 0.94

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
39
If you toss a fair coin 3 times, what is the probability of getting all heads? Express the probability as a simplified fraction.
A)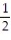
B)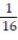
C)
D)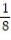
A)
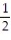
B)
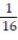
C)

D)
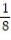

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
40
The probability that a region prone to hurricanes will be hit by a hurricane in any single year is 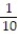 . What is the probability of a hurricane at least once in the next 5 years?
. What is the probability of a hurricane at least once in the next 5 years?
A) 0.99999
B)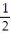
C) 0.40951
D) 0.00001
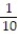 . What is the probability of a hurricane at least once in the next 5 years?
. What is the probability of a hurricane at least once in the next 5 years?A) 0.99999
B)
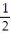
C) 0.40951
D) 0.00001

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
41
Find the indicated probability. If necessary, round to three decimal places.
-Suppose that E and F are two events and that P(E and F) = 0.34 and P(E)= 0.4. What is P( E)?
E)?
A) 0.85
B) 0.74
C) 1.176
D) 0.136
-Suppose that E and F are two events and that P(E and F) = 0.34 and P(E)= 0.4. What is P(
 E)?
E)?A) 0.85
B) 0.74
C) 1.176
D) 0.136

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
42
Find the indicated probability. If necessary, round to three decimal places.
-Suppose that E and F are two events and that N(E and F) = 440 and N(E) = 710. What is P( E)=0.9.What is P(E and F)?
E)=0.9.What is P(E and F)?
A) 1.614
B) 0.383
C) 0.62
D) 0.062
-Suppose that E and F are two events and that N(E and F) = 440 and N(E) = 710. What is P(
 E)=0.9.What is P(E and F)?
E)=0.9.What is P(E and F)?A) 1.614
B) 0.383
C) 0.62
D) 0.062

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
43
Find the indicated probability. If necessary, round to three decimal places.
-Suppose that E and F are two events and that P(E) = 0.4 and P( E) = 0.9. What is P(E andF) ?
E) = 0.9. What is P(E andF) ?
A) 0.36
B) 0.444
C) 1.3
D) 0.036
-Suppose that E and F are two events and that P(E) = 0.4 and P(
 E) = 0.9. What is P(E andF) ?
E) = 0.9. What is P(E andF) ?A) 0.36
B) 0.444
C) 1.3
D) 0.036

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
44
Find the indicated probability. Give your answer as a simplified fraction.
-The overnight shipping business has skyrocketed in the last ten years. The single greatest predictor of a company's success has been proven time and again to be customer service. A study was conducted to study the customer satisfaction levels for one overnight shipping business. In addition to the customer's satisfaction level, the customers were asked how often they used overnight shipping. The results are shown below in the following table. A customer is chosen at random. Given that the customer uses the company less than two times per month, what is the probability that they expressed high satisfaction with the company?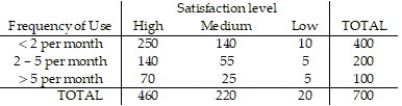
A)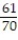
B)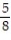
C)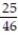
D)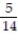
-The overnight shipping business has skyrocketed in the last ten years. The single greatest predictor of a company's success has been proven time and again to be customer service. A study was conducted to study the customer satisfaction levels for one overnight shipping business. In addition to the customer's satisfaction level, the customers were asked how often they used overnight shipping. The results are shown below in the following table. A customer is chosen at random. Given that the customer uses the company less than two times per month, what is the probability that they expressed high satisfaction with the company?

A)
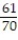
B)
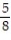
C)
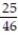
D)
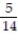

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
45
Find the indicated probability. Give your answer as a simplified fraction.
-A study was recently done that emphasized the problem we all face with drinking and driving. Four hundred accidents that occurred on a Saturday night were analyzed. Two items noted were the number of vehicles involved and whether alcohol played a role in the accident. The numbers are shown below. Given that an accident involved multiple vehicles, what is the probability that it involved alcohol?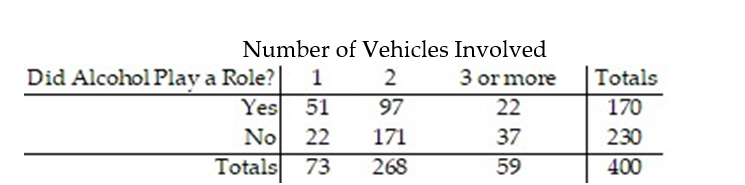
A)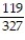
B)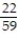
C)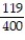
D)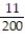
-A study was recently done that emphasized the problem we all face with drinking and driving. Four hundred accidents that occurred on a Saturday night were analyzed. Two items noted were the number of vehicles involved and whether alcohol played a role in the accident. The numbers are shown below. Given that an accident involved multiple vehicles, what is the probability that it involved alcohol?

A)
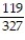
B)
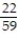
C)
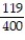
D)
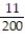

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
46
Find the indicated probability. Give your answer as a simplified fraction.
-A researcher at a large university wanted to investigate if a student's seat preference was related in any way to the gender of the student. The researcher divided the lecture room into three sections (1-front, middle of the room, 2-front, sides of the classroom, and 3-back of the classroom, both middle and sides) and noted where his students sat on a particular day of the class. The researcher's summary table is provided below. Suppose a person sitting in the front, middle portion of the class is randomly selected to answer a question. Find the probability the person selected is a female.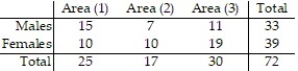
A)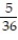
B)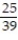
C)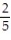
D)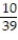
-A researcher at a large university wanted to investigate if a student's seat preference was related in any way to the gender of the student. The researcher divided the lecture room into three sections (1-front, middle of the room, 2-front, sides of the classroom, and 3-back of the classroom, both middle and sides) and noted where his students sat on a particular day of the class. The researcher's summary table is provided below. Suppose a person sitting in the front, middle portion of the class is randomly selected to answer a question. Find the probability the person selected is a female.

A)
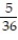
B)
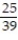
C)
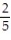
D)
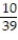

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
47
Find the indicated probability. Give your answer as a simplified fraction.
-The manager of a used car lot took inventory of the automobiles on his lot and constructed the following table based on the age of his car and its make (foreign or domestic).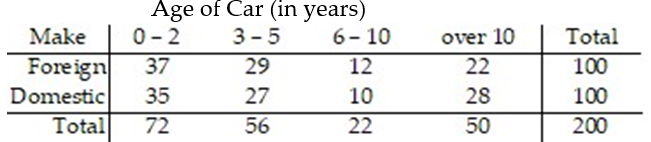 A car was randomly selected from the lot. Given that the car selected is older than two years old, find the probability that it is not a foreign car.
A car was randomly selected from the lot. Given that the car selected is older than two years old, find the probability that it is not a foreign car.
A)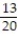
B)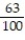
C)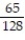
D)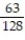
-The manager of a used car lot took inventory of the automobiles on his lot and constructed the following table based on the age of his car and its make (foreign or domestic).
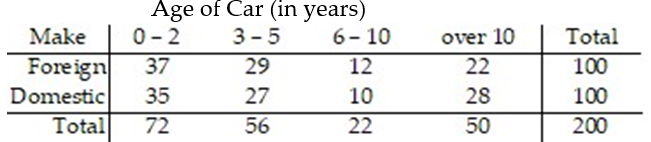 A car was randomly selected from the lot. Given that the car selected is older than two years old, find the probability that it is not a foreign car.
A car was randomly selected from the lot. Given that the car selected is older than two years old, find the probability that it is not a foreign car.A)
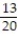
B)
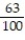
C)
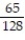
D)
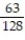

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
48
Find the indicated probability. Give your answer as a decimal rounded to the nearest thousandth.
-A local country club has a membership of 600 and operates facilities that include an 18-hole championship golf course and 12 tennis courts. Before deciding whether to accept new members, the club president would like to know how many members regularly use each facility. A survey of the membership indicates that 68% regularly use the golf course, 44% regularly use the tennis courts, and 10% use neither of these facilities regularly. Given that a randomly selected member uses the tennis courts regularly, find the probability that they also use the golf course regularly.
A) 0.244
B) 0.324
C) 0.5
D) 0.196
-A local country club has a membership of 600 and operates facilities that include an 18-hole championship golf course and 12 tennis courts. Before deciding whether to accept new members, the club president would like to know how many members regularly use each facility. A survey of the membership indicates that 68% regularly use the golf course, 44% regularly use the tennis courts, and 10% use neither of these facilities regularly. Given that a randomly selected member uses the tennis courts regularly, find the probability that they also use the golf course regularly.
A) 0.244
B) 0.324
C) 0.5
D) 0.196

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
49
Four employees drive to work in the same car. The workers claim they were late to work because of a flat tire. Their managers ask the workers to identify the tire that went flat; front driver's side, front passenger's side, rear driver's side, or rear passenger's side. If the workers didn't really have a flat tire and each randomly selects a tire, what is the probability that all four workers select the same tire?
A)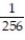
B)
C)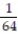
D)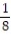
A)
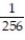
B)

C)
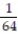
D)
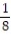

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
50
CampusFest is a student festival where local businesses come on campus to sell their goods to students at vastly reduced prices. As part of a give-away promotion, a local cellular phone company gave away 500 cellular phones to students who signed up for their calling service. Unbeknownst to the company is that 60 of these cellular phones were faulty and will cause a small explosion when dialed outside the local calling area. Suppose you and your roommate each received one of the giveaway phones. Find the probability that both of you received faulty phones. Round to five decimal places when necessary.
A) 0.10581
B) 0.0144
C) 0.24
D) 0.01419
A) 0.10581
B) 0.0144
C) 0.24
D) 0.01419

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
51
Assume that P(A) = 0.7 and P(B) = 0.2. If A and B are independent, find P(A and B).
A) 1.00
B) 0.90
C) 0.14
D) 0.76
A) 1.00
B) 0.90
C) 0.14
D) 0.76

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
52
If P(A) = 0.45, P(B) = 0.25, and P(B|A) = 0.45, are A and B independent?
A) cannot determine
B) no
C) yes
A) cannot determine
B) no
C) yes

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
53
If P(A) = 0.72, P(B) = 0.11, and A and B are independent, find P(A|B).
A) 0.72
B) 0.0792
C) 0.11
D) 0.83
A) 0.72
B) 0.0792
C) 0.11
D) 0.83

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
54
Assume that P(E) = 0.15 and P(F) = 0.48. If E and F are independent, find P(E and F) .
A) 0.072
B) 0.15
C) 0.630
D) 0.558
A) 0.072
B) 0.15
C) 0.630
D) 0.558

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
55
For two events A and B, suppose P(A) = 0.35, P(B) = 0.65, and P(B|A) = 0.35. Then A and B are independent.

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
56
For two events A and B, suppose P(A) = 0.1, P(B) = 0.8, and P(A|B) = 0.1. Then A and B are independent.

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the factorial expression.
-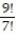
A)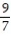
B) 9
C) 72
D) 2!
-
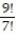
A)
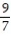
B) 9
C) 72
D) 2!

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the factorial expression.
-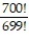
A) 1
B) 489,300
C) 700
D) 699
-
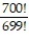
A) 1
B) 489,300
C) 700
D) 699

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
59
0! = 1!

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
60
Find the value of the permutation.
-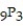
A) 362,880
B) 60,480
C) 504
D) 120,960
-
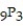
A) 362,880
B) 60,480
C) 504
D) 120,960

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
61
Find the value of the permutation.
-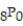
A) 80
B) 1
C) 40,320
D) 0
-
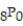
A) 80
B) 1
C) 40,320
D) 0

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
62
Find the value of the permutation.
-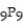
A) 1
B) 362,880
C) 181,440
D) 2
-
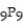
A) 1
B) 362,880
C) 181,440
D) 2

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
63
Find the value of the combination.
-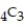
A) 4
B) 12
C) 3
D) 24
-
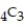
A) 4
B) 12
C) 3
D) 24

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
64
Find the value of the combination.
-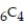
A) 180
B) 4
C) 15
D) 30
-
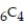
A) 180
B) 4
C) 15
D) 30

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
65
Find the value of the combination.
-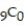
A) 1
B) 181,440
C) 9
D) 90,720
-
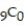
A) 1
B) 181,440
C) 9
D) 90,720

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
66
Find the value of the combination.
-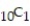
A) 5
B) 725,760
C) 3,628,800
D) 10
-
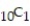
A) 5
B) 725,760
C) 3,628,800
D) 10

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
67
Find the value of the combination.
-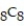
A) 0.5
B) 1
C) 40,320
D) 10,080
-
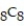
A) 0.5
B) 1
C) 40,320
D) 10,080

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
68
Find the value of the combination.
-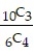
A) 40,320
B) 2
C) 8
D) 4
-
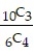
A) 40,320
B) 2
C) 8
D) 4

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
69
In how many ways can a committee of three men and four women be formed from a group of 8 men and 8 women?
A) 564,480
B) 560
C)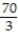
D) 3920
A) 564,480
B) 560
C)
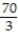
D) 3920

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
70
Six students, A, B, C, D, E, F, are to give speeches to the class. The order of speaking is determined by random selection. Find the probability that (a) E will speak first (b) that C will speak fifth and B will speak last (c) that the students will speak in the following order: DECABF (d) that A or B will speak first.
A)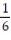 ;
; 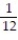 ;
; 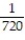 ;
; 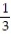
B)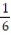 ;
; 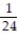 ;
; 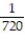 ;
; 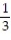
C)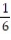 ;
; 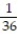 ;
; 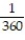 ;
; 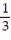
D)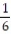 ;
; 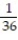 ;
; 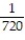 ;
; 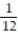
A)
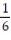 ;
; 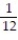 ;
; 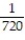 ;
; 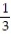
B)
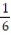 ;
; 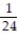 ;
; 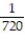 ;
; 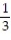
C)
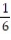 ;
; 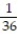 ;
; 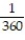 ;
; 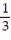
D)
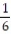 ;
; 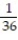 ;
; 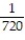 ;
; 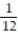

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
71
To play the lottery in a certain state, a person has to correctly select 5 out of 45 numbers, paying $1 for each five-number selection. If the five numbers picked are the same as the ones drawn by the lottery, an enormous sum of money is bestowed. What is the probability that a person with one combination of five numbers will win? What is the probability of winning if 100 different lottery tickets are purchased?
A)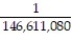 ;
; 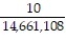
B)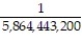 ;
; 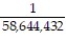
C)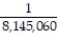 ;
; 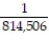
D)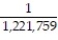 ;
; 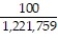
A)
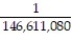 ;
; 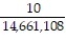
B)
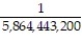 ;
; 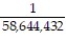
C)
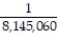 ;
; 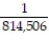
D)
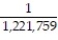 ;
; 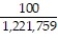

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
72
A box contains 25 widgets, 4 of which are defective. If 4 are sold at random, find the probability that (a) all are defective (b) none are defective.
A)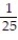 ;
; 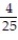
B)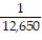 ;
; 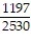
C)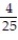 ;
; 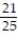
D)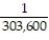 ;
; 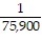
A)
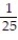 ;
; 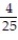
B)
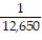 ;
; 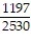
C)
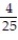 ;
; 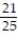
D)
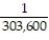 ;
; 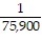

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
73
If you are dealt 5 cards from a shuffled deck of 52 cards, find the probability that all 5 cards are picture cards.
A)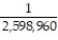
B)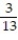
C)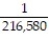
D)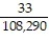
A)
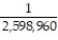
B)
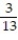
C)
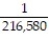
D)
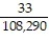

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
74
If you are dealt 5 cards from a shuffled deck of 52 cards, find the probability that none of the 5 cards are picture cards.
A)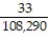
B)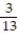
C)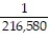
D)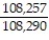
A)
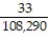
B)
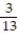
C)
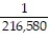
D)
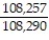

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
75
If you are dealt 6 cards from a shuffled deck of 52 cards, find the probability of getting 3 jacks and 3 aces.
A)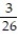
B)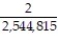
C)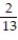
D)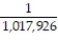
A)
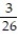
B)
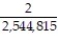
C)
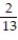
D)
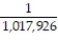

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
76
In how many ways can a committee of three men and four women be formed from a group of 8 men and 8 women?
A) 564,480
B)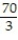
C) 3920
D) 560
A) 564,480
B)
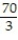
C) 3920
D) 560

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
77
(a) Roll a pair of dice 40 times, recording the sum each time. Use your results to approximate the probability of getting a sum of 8.
(b) Roll a pair of dice 100 times, recording the sum each time. Use your results to approximate the probability of getting a sum of 8.
Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which answer was closer to the probability that would be obtained using the classical method? Is this what you would expect?
(b) Roll a pair of dice 100 times, recording the sum each time. Use your results to approximate the probability of getting a sum of 8.
Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which answer was closer to the probability that would be obtained using the classical method? Is this what you would expect?

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
78
(a) Simulate the experiment of sampling 100 four-child families to estimate the probability that a four-child family has three girls. Assume that the outcomes "have a girl" and "have a boy" are equally likely.
(b) Simulate the experiment of sampling 1000 four-child families to estimate the probability that a four-child family has three girls. Assume that the outcomes "have a girl" and "have a boy" are equally likely.The classical probability that a four-child family has three girls is .
.
Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which answer was closer to the probability that would be obtained using the classical method? Is this what you would expect?
(b) Simulate the experiment of sampling 1000 four-child families to estimate the probability that a four-child family has three girls. Assume that the outcomes "have a girl" and "have a boy" are equally likely.The classical probability that a four-child family has three girls is
 .
.Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which answer was closer to the probability that would be obtained using the classical method? Is this what you would expect?

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
79
(a) Use a graphing calculator or statistical software to simulate drawing a card from a standard deck 100 times (with replacement of the card after each draw). Use an integer distribution with numbers 1 through 4 and use the results of the simulation to estimate the probability of getting a spade when a card is drawn from a standard deck.
(b) Simulate drawing a card from a standard deck 400 times (with replacement of the card after each draw). Estimate the probability of getting a spade when a card is drawn from a standard deck.
Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which simulation resulted in the closest estimate to the probability that would be obtained using the classical method? Is this what you would expect?
(b) Simulate drawing a card from a standard deck 400 times (with replacement of the card after each draw). Estimate the probability of getting a spade when a card is drawn from a standard deck.
Compare the results of (a) and (b) to the probability that would be obtained using the classical method.Which simulation resulted in the closest estimate to the probability that would be obtained using the classical method? Is this what you would expect?

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck
80
Find the indicated probability.
-Find P(A or B) given that P(A) = 0.7, P(B) = 0.1, and A and B are mutually exclusive.
A) 0.8
B) 0
C) 0.6
D) 0.07
-Find P(A or B) given that P(A) = 0.7, P(B) = 0.1, and A and B are mutually exclusive.
A) 0.8
B) 0
C) 0.6
D) 0.07

Unlock Deck
Unlock for access to all 91 flashcards in this deck.
Unlock Deck
k this deck


