Deck 12: Modeling Randomness
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 12: Modeling Randomness
1
Your brother says he is better than you at playing some video game. You play 6 games and he wins 4 of them. He says that this proves he is a better player. You have studied statistics and you want to determine the probability of anyone winning at least 4 games out of 6 just by chance if you are both equally as skilled. Which of the following would provide an accurate estimate of that probability?
A) Take 6 cards and write "win" on 4 of them and "lose" on 2 of them. Shuffle the cards and place them in two piles and determine if one pile has more "win" cards than the other. Repeat this many times. Calculate the proportion of times one pile had more wins than the other.
B) Toss a six-sided die many times and calculate the proportion of times the number 4 or more lands face up.
C) Flip a coin 6 times and count the number of heads. Repeat this many times. Calculate the proportion of your simulated results that gave 4 or more heads.
A) Take 6 cards and write "win" on 4 of them and "lose" on 2 of them. Shuffle the cards and place them in two piles and determine if one pile has more "win" cards than the other. Repeat this many times. Calculate the proportion of times one pile had more wins than the other.
B) Toss a six-sided die many times and calculate the proportion of times the number 4 or more lands face up.
C) Flip a coin 6 times and count the number of heads. Repeat this many times. Calculate the proportion of your simulated results that gave 4 or more heads.
Flip a coin 6 times and count the number of heads. Repeat this many times. Calculate the proportion of your simulated results that gave 4 or more heads.
2
There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee.
-If we record the sex of the chosen committee members (male or female) and their roles (head or not), how many possible outcomes are in the sample space?
A) 1
B) 2
C) 3
D) 4
-If we record the sex of the chosen committee members (male or female) and their roles (head or not), how many possible outcomes are in the sample space?
A) 1
B) 2
C) 3
D) 4
4
3
There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee.
-The events in the sample space are all equally likely.
-The events in the sample space are all equally likely.
False
4
There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee.
-How could you simulate this random process?
A) Roll a six-sided die twice. If the first roll is a one, then the committee head is female; if the second roll is a one, then the other committee member is also female.
B) Write male on seven cards and female on three cards. Select one card to be the committee head, and another card to be the other committee member.
C) Flip a coin twice. If the first flip lands on heads, then the committee head is female; if the second coin lands on heads, then the other committee member is also female.
-How could you simulate this random process?
A) Roll a six-sided die twice. If the first roll is a one, then the committee head is female; if the second roll is a one, then the other committee member is also female.
B) Write male on seven cards and female on three cards. Select one card to be the committee head, and another card to be the other committee member.
C) Flip a coin twice. If the first flip lands on heads, then the committee head is female; if the second coin lands on heads, then the other committee member is also female.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee.
-Now, instead of recording the sex and role of the selected committee members, you only record the number of females selected. How many possible outcomes are in this new sample space?
A) 1
B) 2
C) 3
D) 4
-Now, instead of recording the sex and role of the selected committee members, you only record the number of females selected. How many possible outcomes are in this new sample space?
A) 1
B) 2
C) 3
D) 4

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee.
-A simulation of this random process was run 1,000 times, and the number of females selected for the committee was recorded on each simulation. A bar plot of the results follows.
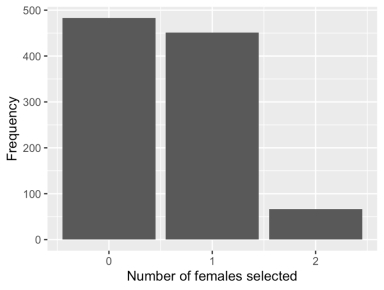 Use the bar plot to estimate the probability that zero females are selected for the committee.
Use the bar plot to estimate the probability that zero females are selected for the committee.
-A simulation of this random process was run 1,000 times, and the number of females selected for the committee was recorded on each simulation. A bar plot of the results follows.
 Use the bar plot to estimate the probability that zero females are selected for the committee.
Use the bar plot to estimate the probability that zero females are selected for the committee.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
7
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-How many possible outcomes are in this sample space?
A) 2
B) 3
C) 4
D) 5
-How many possible outcomes are in this sample space?
A) 2
B) 3
C) 4
D) 5

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-If a person does not have ESP, what is the probability the person's guess is correct?
A) 0.10
B) 0.20
C) 0.50
D) 0.80
-If a person does not have ESP, what is the probability the person's guess is correct?
A) 0.10
B) 0.20
C) 0.50
D) 0.80

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-How could you simulate one play of the game, assuming the participant did not have ESP abilities?
A) Flip a coin five times and count the number of heads that appear.
B) Spin a spinner where 1/5th of the spinner is red and 4/5ths are white. Record whether you land on the red portion of the spinner or not.
C) Take five cards where one card is black and the other four are white. Shuffle the cards and select one card from the five. Record whether you chose a white card or not.
-How could you simulate one play of the game, assuming the participant did not have ESP abilities?
A) Flip a coin five times and count the number of heads that appear.
B) Spin a spinner where 1/5th of the spinner is red and 4/5ths are white. Record whether you land on the red portion of the spinner or not.
C) Take five cards where one card is black and the other four are white. Shuffle the cards and select one card from the five. Record whether you chose a white card or not.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-The ESP test website states: "Keep in mind that your results should only be considered suggestive, because high scores in these tests can be due to chance as well as to actual abilities. Only repeated testing can distinguish between luck and genuine psi abilities." Suppose you take the test five times. How would you simulate the probability of choosing the correct card in at least three of the trials, assuming you do not have ESP?
A) Flip a coin five times and count the number of heads that appear. Repeat this many times. Calculate the proportion of your simulated results that gave 3 or more heads.
B) Spin a spinner five times, where 1/5th of the spinner is red and 4/5ths are white. Record the number of times the spinner lands on white. Repeat this many times. Calculate the proportion of your simulated results where the spinner landed on white at least three times.
C) Take five cards where one card is black and the other four are white. Shuffle the cards and choose five cards with replacement. Record the number of black cards chosen. Repeat this many times. Calculate the proportion of your simulated results where you chose least three black cards.
-The ESP test website states: "Keep in mind that your results should only be considered suggestive, because high scores in these tests can be due to chance as well as to actual abilities. Only repeated testing can distinguish between luck and genuine psi abilities." Suppose you take the test five times. How would you simulate the probability of choosing the correct card in at least three of the trials, assuming you do not have ESP?
A) Flip a coin five times and count the number of heads that appear. Repeat this many times. Calculate the proportion of your simulated results that gave 3 or more heads.
B) Spin a spinner five times, where 1/5th of the spinner is red and 4/5ths are white. Record the number of times the spinner lands on white. Repeat this many times. Calculate the proportion of your simulated results where the spinner landed on white at least three times.
C) Take five cards where one card is black and the other four are white. Shuffle the cards and choose five cards with replacement. Record the number of black cards chosen. Repeat this many times. Calculate the proportion of your simulated results where you chose least three black cards.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-A simulation of this random process was run 1,000 times, assuming the participant did not have ESP, and the number of correct guesses was recorded on each simulation. A bar plot of the results follows.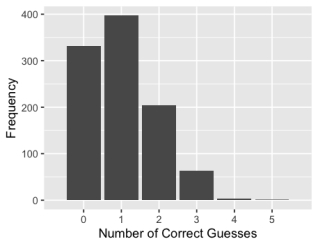 Using the bar plot, estimate the probability of three or more correct guesses.
Using the bar plot, estimate the probability of three or more correct guesses.
A) 0.01
B) 0.04
C) 0.07
D) 0.60
-A simulation of this random process was run 1,000 times, assuming the participant did not have ESP, and the number of correct guesses was recorded on each simulation. A bar plot of the results follows.
 Using the bar plot, estimate the probability of three or more correct guesses.
Using the bar plot, estimate the probability of three or more correct guesses.A) 0.01
B) 0.04
C) 0.07
D) 0.60

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
12
An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct.
-Based on the simulation results in the bar plot, if someone guessed correctly four times, would you consider this evidence that the person has ESP?
A) Yes, since the probability the person does not have ESP is less than 1%.
B) Yes, since if they did not have ESP, the probability of four or more correct guesses is less than 1%.
C) No, since they did not guess all five correctly.
D) No, since it's still possible for a person to guess correctly four times if they don't have ESP.
-Based on the simulation results in the bar plot, if someone guessed correctly four times, would you consider this evidence that the person has ESP?
A) Yes, since the probability the person does not have ESP is less than 1%.
B) Yes, since if they did not have ESP, the probability of four or more correct guesses is less than 1%.
C) No, since they did not guess all five correctly.
D) No, since it's still possible for a person to guess correctly four times if they don't have ESP.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
According to my neighbor, the probability that the tomato plants she planted last month will actually survive to produce fruit is only 0.6. This means her tomato plants will survive to produce fruit in the next six out of 10 growing seasons.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
The probability of an event is always equal to the number of outcomes in the event divided by the number of outcomes in the sample space.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
According to Krantz in his book What the Odds Are (1992, p. 161), the probability that a randomly selected American will be injured by lightning in a given year is 1/685000. What does this probability mean?
A) Every 1 out of 685,000 Americans will be injured by lightning in a given year.
B) If we were to randomly select an American many many times, then the proportion of times that selected American would be injured by lightning in a given year is 1/685000.
C) If we were to randomly select 100 Americans, none of them would be injured by lightning in a given year.
D) Out of 685,000 years, no one will get injured by lightning in 684,999 of those years.
A) Every 1 out of 685,000 Americans will be injured by lightning in a given year.
B) If we were to randomly select an American many many times, then the proportion of times that selected American would be injured by lightning in a given year is 1/685000.
C) If we were to randomly select 100 Americans, none of them would be injured by lightning in a given year.
D) Out of 685,000 years, no one will get injured by lightning in 684,999 of those years.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
Assume that, for events and , and . Are and are mutually exclusive?
A) Yes
B) No
C) We do not have enough information to determine whether and are mutually exclusive.
A) Yes
B) No
C) We do not have enough information to determine whether and are mutually exclusive.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
John is taking Statistics and Biology this semester. The probability John will get an A in Statistics is 0.4. The probability John will get an A in Biology is 0.3. The probability John will get an A in both Statistics and Biology is 0.15. What is the probability that John will get at least one A between his Statistics and Biology courses?
A) 0.12
B) 0.15
C) 0.55
D) 0.7
A) 0.12
B) 0.15
C) 0.55
D) 0.7

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Write the probability 0.42 in probability notation.
A) P(M)
B) P(R)
C) P(R?M)
D) P(R?M)
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Write the probability 0.42 in probability notation.
A) P(M)
B) P(R)
C) P(R?M)
D) P(R?M)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-How would you write the event that a college student "does not participate in a campus meal program" in probability notation?
A) P(M)
B) P(MC )
C) P(R?MC )
D) P(RC ?M)
R = student lives in a campus residence hall
M = student participates in a campus meal program
-How would you write the event that a college student "does not participate in a campus meal program" in probability notation?
A) P(M)
B) P(MC )
C) P(R?MC )
D) P(RC ?M)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-How would you write the event that a college student "lives on campus and does not participate in a campus meal program" in probability notation?
A) P(M)
B) P(MC )
C) P(R?MC )
D) P(RC ?M)
R = student lives in a campus residence hall
M = student participates in a campus meal program
-How would you write the event that a college student "lives on campus and does not participate in a campus meal program" in probability notation?
A) P(M)
B) P(MC )
C) P(R?MC )
D) P(RC ?M)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(RC).
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(RC).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(MC).
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(MC).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Use the addition rule to find P(R U M).
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Use the addition rule to find P(R U M).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Are the events and mutually exclusive?
A) Yes
B) No
C) Not enough information provided
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Are the events and mutually exclusive?
A) Yes
B) No
C) Not enough information provided

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Fill in the probability table below to represent this scenario.

R = student lives in a campus residence hall
M = student participates in a campus meal program
-Fill in the probability table below to represent this scenario.


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Suppose there are 100 students in this population. Fill in the Venn diagram below to represent the number of students in each category for this scenario. Hint: The four numbers should sum to 100!
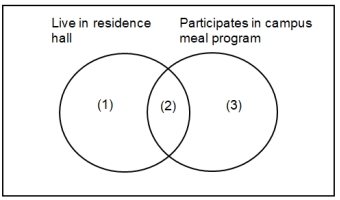
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Suppose there are 100 students in this population. Fill in the Venn diagram below to represent the number of students in each category for this scenario. Hint: The four numbers should sum to 100!


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
A lightbulb manufacturing plant's production line has determined that the probability a lightbulb will be defective is 0.04. The quality control team decides to take a random sample of 500 lightbulbs and measure the proportion of those lightbulbs that are defective.
-Use the Normal Probability Calculator applet to approximate the probability the quality control team sees at least 25 defective items in their sample.
-Use the Normal Probability Calculator applet to approximate the probability the quality control team sees at least 25 defective items in their sample.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
Suppose you roll a six-sided die once. Define events
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Are events B and C mutually exclusive?
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Are events B and C mutually exclusive?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose you roll a six-sided die once. Define events
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(BC).
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(BC).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose you roll a six-sided die once. Define events
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(A∪B).
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(A∪B).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose you roll a six-sided die once. Define events
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(C∪D).
A = roll an even number
B = roll a two
C = roll an odd number
D = roll a number greater than three
-Find P(C∪D).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.39, and winning is independent from one bottle to the next. You buy six bottles. What is the probability that none of the six bottles reveals a prize?
A) 0.39
B) 0.61
C) 0.052
D) 0.004
A) 0.39
B) 0.61
C) 0.052
D) 0.004

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
33
Assume that events A and B are independent, where P(A)=0.3 and P(B)=0.6. What is P(A|B)?
A) 0.6
B) 0.3
C) 0.18
D) 0
A) 0.6
B) 0.3
C) 0.18
D) 0

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
Assume that events and are mutually exclusive, where and . What is ?
A) 0.6
B) 0.3
C) 0.18
D) 0
A) 0.6
B) 0.3
C) 0.18
D) 0

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Are the events and independent?
A) Yes
B) No
C) Not enough information provided
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Are the events and independent?
A) Yes
B) No
C) Not enough information provided

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-What is the appropriate expression for the probability that a randomly chosen college student who lives in a campus residence hall participates in a campus meal program?
A) P(R?M)
B) P(M?R)
C) P(M?R)
D) P(M?R)
R = student lives in a campus residence hall
M = student participates in a campus meal program
-What is the appropriate expression for the probability that a randomly chosen college student who lives in a campus residence hall participates in a campus meal program?
A) P(R?M)
B) P(M?R)
C) P(M?R)
D) P(M?R)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(R│M)..
R = student lives in a campus residence hall
M = student participates in a campus meal program
-Find P(R│M)..

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose that 70% of the seniors at a large university have taken calculus, and 30% of the seniors have taken physics. Of the seniors who have taken calculus, 40% have taken physics. A student who is a senior at this university is randomly selected. Define the following events.
A = The student has taken calculus
B = The student has taken physics
-Which of the following is true about the events A and B?
A) A and B are mutually exclusive.
B) A and B are complements.
C) A and B are independent.
D) None of the above.
A = The student has taken calculus
B = The student has taken physics
-Which of the following is true about the events A and B?
A) A and B are mutually exclusive.
B) A and B are complements.
C) A and B are independent.
D) None of the above.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose that 70% of the seniors at a large university have taken calculus, and 30% of the seniors have taken physics. Of the seniors who have taken calculus, 40% have taken physics. A student who is a senior at this university is randomly selected. Define the following events.
A = The student has taken calculus
B = The student has taken physics
-Find P(A?B)
A) 0.70 + 0.30 - 0.40 = 0.6
B) (0.70)(0.30) = 0.21
C) (0.70)(0.40) = 0.28
D) (0.30)(0.40) = 0.12
A = The student has taken calculus
B = The student has taken physics
-Find P(A?B)
A) 0.70 + 0.30 - 0.40 = 0.6
B) (0.70)(0.30) = 0.21
C) (0.70)(0.40) = 0.28
D) (0.30)(0.40) = 0.12

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
Data on sex and opinion on the death penalty for respondents in the 2008 General Social Survey in which a random sample of 1,902 adults in the U.S. was surveyed are below. 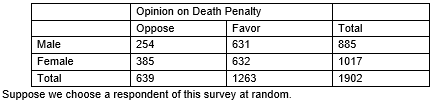
-What is the probability that the respondent will oppose the death penalty, given that the respondent is male?
A) 254/1902
B) 639/1902
C) 254/639
D) 254/885

-What is the probability that the respondent will oppose the death penalty, given that the respondent is male?
A) 254/1902
B) 639/1902
C) 254/639
D) 254/885

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
Data on sex and opinion on the death penalty for respondents in the 2008 General Social Survey in which a random sample of 1,902 adults in the U.S. was surveyed are below. 
-What is the probability that the respondent is female and opposes the death penalty?
A) 385/1902
B) 385/639
C) 385/1017
D) 639/1902

-What is the probability that the respondent is female and opposes the death penalty?
A) 385/1902
B) 385/639
C) 385/1017
D) 639/1902

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-For each of the given probabilities, state whether the probability is a conditional probability or an unconditional probability:
0.08?
0.90?
0.85?
A = person has the disease
B = person tests positive on the diagnostic test
-For each of the given probabilities, state whether the probability is a conditional probability or an unconditional probability:
0.08?
0.90?
0.85?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-How would you express the probability 0.90 in terms of A and B?
A) P(A)
B) P(B)
C) P(A?B)
D) P(B?A)
E) P(A?B) F. P(A?B)
A = person has the disease
B = person tests positive on the diagnostic test
-How would you express the probability 0.90 in terms of A and B?
A) P(A)
B) P(B)
C) P(A?B)
D) P(B?A)
E) P(A?B) F. P(A?B)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-Fill in the values below to create a hypothetical table of 1,000 randomly selected individuals in this population.
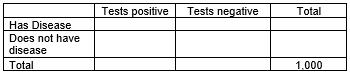
A = person has the disease
B = person tests positive on the diagnostic test
-Fill in the values below to create a hypothetical table of 1,000 randomly selected individuals in this population.


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-Fill in the tree diagram below to represent this scenario.
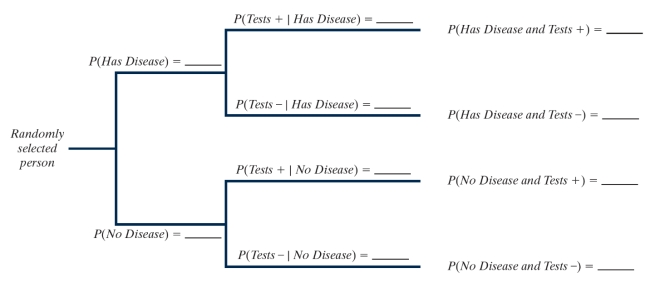
A = person has the disease
B = person tests positive on the diagnostic test
-Fill in the tree diagram below to represent this scenario.


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-What is the probability that a randomly selected person tests positive on the diagnostic test?
A = person has the disease
B = person tests positive on the diagnostic test
-What is the probability that a randomly selected person tests positive on the diagnostic test?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events:
A = person has the disease
B = person tests positive on the diagnostic test
-Given that a person tests positive on the diagnostic test, what is the probability he or she has the disease?
A = person has the disease
B = person tests positive on the diagnostic test
-Given that a person tests positive on the diagnostic test, what is the probability he or she has the disease?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
Which of the following variables is a discrete random variable?
A) Time it takes one email to travel between a sender and receiver
B) Number of letters in the last name of a randomly chosen student
C) Weight a dieter will lose after following a two-week weight loss program
D) High temperature in Irvine on a randomly chosen day
A) Time it takes one email to travel between a sender and receiver
B) Number of letters in the last name of a randomly chosen student
C) Weight a dieter will lose after following a two-week weight loss program
D) High temperature in Irvine on a randomly chosen day

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
Which of the following variables is a discrete random variable?
A) Time it takes a randomly selected student to finish this exam
B) Body temperature of a randomly selected adult
C) Distance a randomly selected adult walks in a day
D) Number of texts a randomly selected college student receives in a day
A) Time it takes a randomly selected student to finish this exam
B) Body temperature of a randomly selected adult
C) Distance a randomly selected adult walks in a day
D) Number of texts a randomly selected college student receives in a day

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
The standard deviation of a random variable Y is the…
A) range of possible values for Y.
B) most common value over a large number of observations of Y.
C) approximate average distance from the mean that one would see in a large number of observations of Y.
D) approximate mean value over a large number of observations of Y.
A) range of possible values for Y.
B) most common value over a large number of observations of Y.
C) approximate average distance from the mean that one would see in a large number of observations of Y.
D) approximate mean value over a large number of observations of Y.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. 
-What is the probability that a randomly chosen policy holder claims more than $100?
A) 0.07
B) 0.13
C) 0.20
D) 0.87

-What is the probability that a randomly chosen policy holder claims more than $100?
A) 0.07
B) 0.13
C) 0.20
D) 0.87

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. 
-Calculate the expected value of X.
$_________

-Calculate the expected value of X.
$_________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. 
-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen policyholder to collect $D in claims this year.
B) The most likely value for the amount in claims is $D.
C) If we were to observe a large number of policyholders, the average amount claimed would be around $D.
D) On average, the amount claimed is about $D away from the mean.

-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen policyholder to collect $D in claims this year.
B) The most likely value for the amount in claims is $D.
C) If we were to observe a large number of policyholders, the average amount claimed would be around $D.
D) On average, the amount claimed is about $D away from the mean.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. 
-Calculate the standard deviation of X.
$________

-Calculate the standard deviation of X.
$________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. 
-Let $S be the standard deviation of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen policyholder to collect $S in claims this year.
B) The most likely value for the amount in claims is $S.
C) If we were to observe a large number of policyholders, the average amount claimed would be around $S.
D) On average, the amount claimed is about $S away from the mean.

-Let $S be the standard deviation of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen policyholder to collect $S in claims this year.
B) The most likely value for the amount in claims is $S.
C) If we were to observe a large number of policyholders, the average amount claimed would be around $S.
D) On average, the amount claimed is about $S away from the mean.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Determine the probability distribution of X:

X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Determine the probability distribution of X:


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Calculate E(X).
$_______
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Calculate E(X).
$_______

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen ticket to result in a win of $D.
B) The most likely value for the amount won for a single ticket is $D.
C) The amount won for a single ticket will deviate, on average, from the expected amount won by about $D.
D) If you were to play the instant lottery many times, the average amount won per ticket would be around $D.
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Let $D be the expected value of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen ticket to result in a win of $D.
B) The most likely value for the amount won for a single ticket is $D.
C) The amount won for a single ticket will deviate, on average, from the expected amount won by about $D.
D) If you were to play the instant lottery many times, the average amount won per ticket would be around $D.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Fill in the blank with the correct dollar amount:
If the lottery agency does not want to lose money over the long run, they must charge at least
$_______ per ticket.
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Fill in the blank with the correct dollar amount:
If the lottery agency does not want to lose money over the long run, they must charge at least
$_______ per ticket.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Calculate the standard deviation of X.
$________
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Calculate the standard deviation of X.
$________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Let $S be the standard deviation of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen ticket to result in a win of $D.
B) The most likely value for the amount won for a single ticket is $D.
C) The amount won for a single ticket will deviate, on average, from the expected amount won by about $D.
D) If you were to play the instant lottery many times, the average amount won per ticket would be around $D.
X = amount won for a single ticket. (You can ignore the cost of the ticket.)
-Let $S be the standard deviation of X. Which of the following is a correct interpretation of this value?
A) We would expect a randomly chosen ticket to result in a win of $D.
B) The most likely value for the amount won for a single ticket is $D.
C) The amount won for a single ticket will deviate, on average, from the expected amount won by about $D.
D) If you were to play the instant lottery many times, the average amount won per ticket would be around $D.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
Based on her past experience, a professor knows that the probability distribution function for X = number of students who come to her office hours on any given Wednesday is given below. 
-What is the value of P(X = 4) (the question mark in the table)?
A) 0.05
B) 0.10
C) 0.25
D) 1

-What is the value of P(X = 4) (the question mark in the table)?
A) 0.05
B) 0.10
C) 0.25
D) 1

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
Based on her past experience, a professor knows that the probability distribution function for X = number of students who come to her office hours on any given Wednesday is given below. 
-The expected value of X is 1.85. Interpret this value in the context of the problem.
A) If you were to observe many students, the average number of students that visit office hours is 1.85.
B) If you were to observe many Wednesdays, the average number of students that visit office hours is 1.85.
C) On average, the number of students that visit office hours will deviate from the mean by 1.85.
D) Next Wednesday, we expect 2 students to visit office hours.

-The expected value of X is 1.85. Interpret this value in the context of the problem.
A) If you were to observe many students, the average number of students that visit office hours is 1.85.
B) If you were to observe many Wednesdays, the average number of students that visit office hours is 1.85.
C) On average, the number of students that visit office hours will deviate from the mean by 1.85.
D) Next Wednesday, we expect 2 students to visit office hours.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
Based on her past experience, a professor knows that the probability distribution function for X = number of students who come to her office hours on any given Wednesday is given below. 
-The standard deviation of X is 0.96. Interpret this value in the context of the problem.
A) If you were to observe many students, the average number of students that visit office hours is 0.96.
B) If you were to observe many Wednesdays, the average number of students that visit office hours is 0.96.
C) On average, the number of students that visit office hours will deviate from the mean by about one student.
D) Next Wednesday, we expect one student to visit office hours.

-The standard deviation of X is 0.96. Interpret this value in the context of the problem.
A) If you were to observe many students, the average number of students that visit office hours is 0.96.
B) If you were to observe many Wednesdays, the average number of students that visit office hours is 0.96.
C) On average, the number of students that visit office hours will deviate from the mean by about one student.
D) Next Wednesday, we expect one student to visit office hours.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
Which of the following has a higher expected earning?
Option 1: A gift of $240, guaranteed.
Option 2: A 25% chance to win $1,000, and a 75% chance of getting nothing.
A) Option 1
B) Option 2
C) The two expected earnings are equal.
Option 1: A gift of $240, guaranteed.
Option 2: A 25% chance to win $1,000, and a 75% chance of getting nothing.
A) Option 1
B) Option 2
C) The two expected earnings are equal.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
Which of the following has a larger expected loss?
Option 1: A sure loss of $740.
Option 2: A 25% chance to lose nothing, and a 75% chance of losing $1000.
A) Option 1
B) Option 2
C) The two expected earnings are equal.
Option 1: A sure loss of $740.
Option 2: A 25% chance to lose nothing, and a 75% chance of losing $1000.
A) Option 1
B) Option 2
C) The two expected earnings are equal.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Calculate E(X).
-Calculate E(X).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Express Y as a linear transformation of X.
Y = ___(1)____ X + ____(2)_____
-Express Y as a linear transformation of X.
Y = ___(1)____ X + ____(2)_____

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Use the rules for expected value for linear transformations to find E(Y).
$________
-Use the rules for expected value for linear transformations to find E(Y).
$________

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Based on the expected value, is it worth the $5 to enter?
A) No, since the expected profit is also $5.
B) Yes, since in the long-run, your average net profit is greater than zero.
-Based on the expected value, is it worth the $5 to enter?
A) No, since the expected profit is also $5.
B) Yes, since in the long-run, your average net profit is greater than zero.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Calculate σX2.
-Calculate σX2.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Use the rules for expected value for linear transformations to find σY2.
-Use the rules for expected value for linear transformations to find σY2.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
Consider a game in which a fair die is thrown. The player pays $5 to play and wins $2 for each dot that appears on the roll. Define X = number on which the die lands, and Y = player's net profit (amount won - amount paid to play).
-Find σY.
-Find σY.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. From past data, the insurance company has determined that E(X) = $72, and σ_X = $60.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find E(Y).
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find E(Y).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. From past data, the insurance company has determined that E(X) = $72, and σ_X = $60.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find σY2.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find σY2.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. From past data, the insurance company has determined that E(X) = $72, and σ_X = $60.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find σY.
Suppose the insurance company decides to offer a discount to attract new customers. They will pay the new customer $50 for joining, and offer a 5% "cash back" offer for all claims paid. Let Y be the amount in claims (in dollars) for a randomly chosen new customer. Then Y=50+1.05X.
-Find σY.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
Four friends are contemplating joining a local bowling league. Let X1,X2,X3,X4 be the score of the first, second, third, and fourth friend, respectively, on a randomly chosen game. From past experience, the friends know that: E(X1 )=110, E(X2 )=125, E(X3 )=113, and E(X4 )=140. Additionally, ?1=7, ?1=13, ?1=10, and ?1=20. Define their total score on a randomly chosen game as Y=X1+X2+X3+X4. Assume the four players' scores are independent.
-The friends decide it would only be worth it to join the bowling league if they could average a total score of 500. Should they join the league?
A) Yes, since their expected total score is greater than 500.
B) No, since their expected total score is less than 500.
C) Yes, since it is possible for their total score to be greater than 500 on a randomly chosen game.
D) No, since it is not possible for their total score to be greater than 500 on a randomly chosen game.
-The friends decide it would only be worth it to join the bowling league if they could average a total score of 500. Should they join the league?
A) Yes, since their expected total score is greater than 500.
B) No, since their expected total score is less than 500.
C) Yes, since it is possible for their total score to be greater than 500 on a randomly chosen game.
D) No, since it is not possible for their total score to be greater than 500 on a randomly chosen game.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
Four friends are contemplating joining a local bowling league. Let X1,X2,X3,X4 be the score of the first, second, third, and fourth friend, respectively, on a randomly chosen game. From past experience, the friends know that: E(X1 )=110, E(X2 )=125, E(X3 )=113, and E(X4 )=140. Additionally, σ1=7, σ1=13, σ1=10, and σ1=20. Define their total score on a randomly chosen game as Y=X1+X2+X3+X4. Assume the four players' scores are independent.
-Calculate the variance of their total score on a randomly chosen game.
-Calculate the variance of their total score on a randomly chosen game.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
Four friends are contemplating joining a local bowling league. Let X1,X2,X3,X4 be the score of the first, second, third, and fourth friend, respectively, on a randomly chosen game. From past experience, the friends know that: E(X1 )=110, E(X2 )=125, E(X3 )=113, and E(X4 )=140. Additionally, σ1=7, σ1=13, σ1=10, and σ1=20. Define their total score on a randomly chosen game as Y=X1+X2+X3+X4. Assume the four players' scores are independent.
-Calculate σY.
-Calculate σY.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
Suppose X is a random variable with E(X)=5 and σX2=4. Define Y=2X+8.
-Calculate the expected value of Y.
-Calculate the expected value of Y.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck


