Deck 9: Trigonometric Identities and Their Applications
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 9: Trigonometric Identities and Their Applications
1
The following table gives  , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.  If
If  were approximately trigonometric, its formula could be written
were approximately trigonometric, its formula could be written  . Round the second answer to 3 decimal places.
. Round the second answer to 3 decimal places.
 , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.  If
If  were approximately trigonometric, its formula could be written
were approximately trigonometric, its formula could be written  . Round the second answer to 3 decimal places.
. Round the second answer to 3 decimal places.a)-18
b)0.167
c)45
b)0.167
c)45
2
The following table gives  , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.  Assume that
Assume that  is approximately trigonometric. A second candidate, candidate B, has a percentage of support given by
is approximately trigonometric. A second candidate, candidate B, has a percentage of support given by  . What is the largest value of t,
. What is the largest value of t, 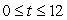 , at which the two candidates are tied for electoral support? Round to 2 decimal places.
, at which the two candidates are tied for electoral support? Round to 2 decimal places.
 , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.  Assume that
Assume that  is approximately trigonometric. A second candidate, candidate B, has a percentage of support given by
is approximately trigonometric. A second candidate, candidate B, has a percentage of support given by  . What is the largest value of t,
. What is the largest value of t, 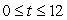 , at which the two candidates are tied for electoral support? Round to 2 decimal places.
, at which the two candidates are tied for electoral support? Round to 2 decimal places.11.39
3
The following table gives , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
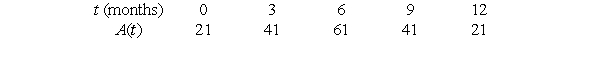 Assume that
Assume that Is approximately trigonometric. A second candidate, candidate B, has a percentage of candidate support given by
Is approximately trigonometric. A second candidate, candidate B, has a percentage of candidate support given by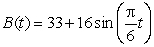 Let
Let For
For
 What is the meaning of the maximum of
What is the meaning of the maximum of ?
?
A) The maximum percentage lead candidate A has over candidate B.
B) The maximum percentage lead candidate B has over candidate A .
C) The maximum combined percentage of the electorate favoring either candidate A or candidate B.
D) The maximum combined percentage of the electorate favoring neither candidate A nor candidate B.
 , the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.
, the percentage of the electorate favoring candidate A during the 12 months preceding a presidential election. Time, t, is measured in months, and t = 0 is a year before election day.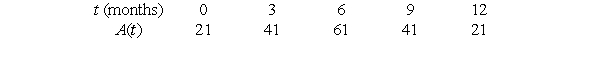 Assume that
Assume that Is approximately trigonometric. A second candidate, candidate B, has a percentage of candidate support given by
Is approximately trigonometric. A second candidate, candidate B, has a percentage of candidate support given by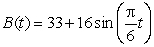 Let
Let For
For What is the meaning of the maximum of
What is the meaning of the maximum of ?
?A) The maximum percentage lead candidate A has over candidate B.
B) The maximum percentage lead candidate B has over candidate A .
C) The maximum combined percentage of the electorate favoring either candidate A or candidate B.
D) The maximum combined percentage of the electorate favoring neither candidate A nor candidate B.
The maximum combined percentage of the electorate favoring either candidate A or candidate B.
4
Two weights (weight 1 and weight 2) are suspended from the ceiling by springs. At time t = 0 (t in seconds), the weights are set in motion and begin bobbing up and down. Eventually, however, the oscillation of both weights dies down. The following equations describe the distance of each weight from the ceiling as a function of time:
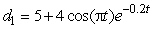 and
and 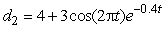 .
.
Which weight is closer to the ceiling at time t = 2?
A) Weight 1
B) Weight 2
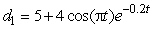 and
and 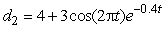 .
.Which weight is closer to the ceiling at time t = 2?
A) Weight 1
B) Weight 2

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
Two weights (weight 1 and weight 2) are suspended from the ceiling by springs. At time t = 0 (t in seconds), the weights are set in motion and begin bobbing up and down. Eventually, however, the oscillation of both weights dies down. The following equations describe the distance of each weight from the ceiling as a function of time:
 and
and  .
.
Which weight has oscillations which die down the fastest?
A) Weight 2
B) Weight 1
 and
and  .
.Which weight has oscillations which die down the fastest?
A) Weight 2
B) Weight 1

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
Two weights (weight 1 and weight 2) are suspended from the ceiling by springs. At time t = 0 (t in seconds), the weights are set in motion and begin bobbing up and down. Eventually, however, the oscillation of both weights dies down. The following equations describe the distance of each weight from the ceiling as a function of time:
 and
and  .
.
At what time are the two weights farthest apart?
A) At t = 0.
B) Between t = 0 and t = 0.5.
C) At t = 0.5.
D) Between t = 0.5 and t = 1.
E) At t = 1.
 and
and  .
.At what time are the two weights farthest apart?
A) At t = 0.
B) Between t = 0 and t = 0.5.
C) At t = 0.5.
D) Between t = 0.5 and t = 1.
E) At t = 1.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Is the square of a complex number always real and nonnegative?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
Find a formula for a deer population which oscillates over a 6 year period between a low of 1000 in year t=0 and a high of 2900 in year t=3 .

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
The deer population in a state park is modelled by  where t is the number of months since January 1, 2005. Evaluate
where t is the number of months since January 1, 2005. Evaluate

and interpret the result. Round to the nearest whole number.
 where t is the number of months since January 1, 2005. Evaluate
where t is the number of months since January 1, 2005. Evaluate
and interpret the result. Round to the nearest whole number.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
The deer population in a state park is modelled by  where t is the number of months since January 1, 2005. If
where t is the number of months since January 1, 2005. If  , find the value(s) of t at which the deer population is equal to 280. Round your answer to the nearest tenth.
, find the value(s) of t at which the deer population is equal to 280. Round your answer to the nearest tenth.
 where t is the number of months since January 1, 2005. If
where t is the number of months since January 1, 2005. If  , find the value(s) of t at which the deer population is equal to 280. Round your answer to the nearest tenth.
, find the value(s) of t at which the deer population is equal to 280. Round your answer to the nearest tenth.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
A ferris wheel sitting on the ground is 24 meters in diameter and makes one revolution every 7 minutes. If you start in the 9 o'clock position t= 0 and the wheel is rotating clockwise, write a formula for your height above the ground at time t.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
A ferris wheel sitting on the ground is 26 meters in diameter and makes one revolution every 7 minutes. If you start in the 9 o'clock position t= 0 and the wheel is rotating counterclockwise, write a formula for your height above the ground at time t.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
A ferris wheel sitting on the ground is 20 meters in diameter and makes one revolution every 7 minutes. If you start in the 9 o'clock position t= 0 and the wheel is rotating counterclockwise, write a formula for your height above the ground at time t.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
A ferris wheel sitting on the ground is 22 meters in diameter and makes one revolution every 5 minutes. If you start in the 9 o'clock position at t= 0 and the wheel is rotating clockwise, when is the first time that are you 16.5 meters above the ground?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
A ferris wheel sitting on the ground is 24 meters in diameter and makes one revolution every 7 minutes. If you start in the 9 o'clock position at t= 0 and the wheel is rotating counterclockwise, when is the first time that are you 6 meters above the ground?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
A mass attached to a spring moves horizontally on a frictionless track. Its displacement from the rest position at time t is given by 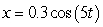 . What is the furthest distance from the rest position that the mass will achieve? The displacement is measured in meters.
. What is the furthest distance from the rest position that the mass will achieve? The displacement is measured in meters.
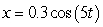 . What is the furthest distance from the rest position that the mass will achieve? The displacement is measured in meters.
. What is the furthest distance from the rest position that the mass will achieve? The displacement is measured in meters.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
A mass attached to a spring moves horizontally on a frictionless track. Its displacement from the rest position at time t is given by  . If displacement is measured in inches and time is measured in inches, when is the mass 0.3 inches from the rest position? Restrict your answer(s) to
. If displacement is measured in inches and time is measured in inches, when is the mass 0.3 inches from the rest position? Restrict your answer(s) to  , and round to 3 decimal places.
, and round to 3 decimal places.
 . If displacement is measured in inches and time is measured in inches, when is the mass 0.3 inches from the rest position? Restrict your answer(s) to
. If displacement is measured in inches and time is measured in inches, when is the mass 0.3 inches from the rest position? Restrict your answer(s) to  , and round to 3 decimal places.
, and round to 3 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
A mass attached to a spring moves horizontally on a frictionless track. Its velocity at time t is given by  . What is the maximum velocity that the mass will achieve? The displacement is measured in meters and the time is measured in seconds.
. What is the maximum velocity that the mass will achieve? The displacement is measured in meters and the time is measured in seconds.
 . What is the maximum velocity that the mass will achieve? The displacement is measured in meters and the time is measured in seconds.
. What is the maximum velocity that the mass will achieve? The displacement is measured in meters and the time is measured in seconds.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
The population in a town oscillates over a 15 year period beginning with a high of 3000 people in year 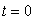 and a low of 2300. Find a formula for the town's population.
and a low of 2300. Find a formula for the town's population.
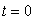 and a low of 2300. Find a formula for the town's population.
and a low of 2300. Find a formula for the town's population.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
The population in a town oscillates over a 7 year period beginning with a high of 3000 people in year t= 0 and a low of 2300. Find a formula for the town's population.
A)
B)
C)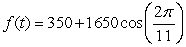
D)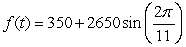
A)

B)

C)
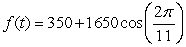
D)
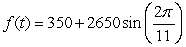

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
Does 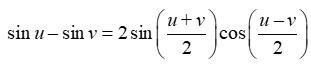 ?
?
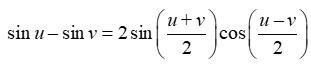 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
If  can also be written in the form
can also be written in the form  .
.
 can also be written in the form
can also be written in the form  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
Does 


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
If 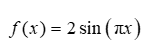 ,can
,can 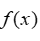 also be written in the form
also be written in the form 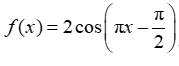 ?
?
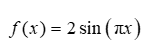 ,can
,can 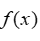 also be written in the form
also be written in the form 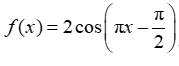 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
Does 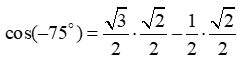 ?
?
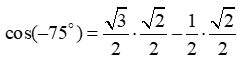 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
Using the sum or difference formulas,  . Round both answers to 4 decimal places.
. Round both answers to 4 decimal places.
 . Round both answers to 4 decimal places.
. Round both answers to 4 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
Using the sum or difference formulas,  . Round all answers to 4 decimal places.
. Round all answers to 4 decimal places.
 . Round all answers to 4 decimal places.
. Round all answers to 4 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
Does  ?
?
 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
Does 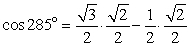 ?
?
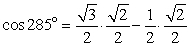 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
Find the exact value of 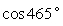 .
.
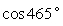 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
Find the exact value of  .
.
 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Find the smallest value of t such that  and
and  .
.
 and
and  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Find the smallest value of t such that  and
and  .
.
 and
and  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
Find the smallest value of t such that 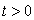 and
and 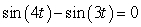
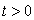 and
and 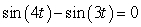

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
Find the smallest value of t such that  and
and  .
.
 and
and  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
Write  in the form
in the form  .
.
 in the form
in the form  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Write  in the form
in the form 
.
 in the form
in the form 
.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
Write  in the form
in the form  .
.
 in the form
in the form  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
Calculate  exactly.
exactly.
 exactly.
exactly.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
Write 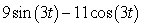 In the form
In the form 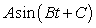
.
A)
B)
C)
D)
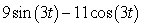 In the form
In the form 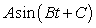
.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
Does  ?
?
 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
What is the smallest positive solution to 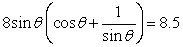 ? Round to 2 decimal places.
? Round to 2 decimal places.
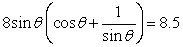 ? Round to 2 decimal places.
? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
What is the smallest positive solution to 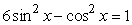 ? Round to 2 decimal places.
? Round to 2 decimal places.
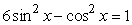 ? Round to 2 decimal places.
? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
How many solutions does 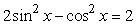 have for
have for 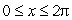 ?
?
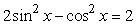 have for
have for 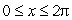 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
What is the smallest positive solution to  ? Round to 2 decimal places.
? Round to 2 decimal places.
 ? Round to 2 decimal places.
? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
How many solutions does  have for
have for  ?
?
 have for
have for  ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
47
Does  ?
?
 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
48
What is the smallest positive solution to 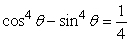 ? Round your answer to 2 decimal places.
? Round your answer to 2 decimal places.
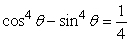 ? Round your answer to 2 decimal places.
? Round your answer to 2 decimal places.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
49
How many solutions does  have for
have for  ?
?
 have for
have for  ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
50
Which of the following statements are identities?
A)
B)
C)
D)
E)
F)
A)

B)

C)

D)

E)

F)


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
What is 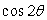 for
for 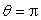 ?
?
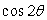 for
for 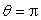 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
Either show the following equation is true, or find a value of x for which the equation is false:
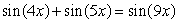
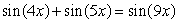

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
Either show the following equation is true, or find a value of x for which the equation is false:



Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
Either show the following equation is true, or find a value of x for which the equation is false:



Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Write 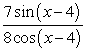 in terms of the tangent function.
in terms of the tangent function.
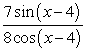 in terms of the tangent function.
in terms of the tangent function.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
Write 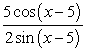 in terms of the cotangent function.
in terms of the cotangent function.
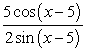 in terms of the cotangent function.
in terms of the cotangent function.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
How many solutions does 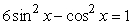 have for
have for 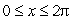 ?
?
A)4
B)0
C)1
D) none of the above.
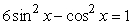 have for
have for 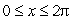 ?
? A)4
B)0
C)1
D) none of the above.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
Write 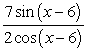 in terms of the tangent function.
in terms of the tangent function.
A)
B)
C)
D)
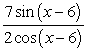 in terms of the tangent function.
in terms of the tangent function.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


