Deck 6: Transportation, Assignment, and Transshipment Problems

Question 1

Transportation and assignment problems can be solved by the simplex method, though special purpose algorithms offer an easier solution procedure.

Answer 1

True

Question 2

The total supply must equal total demand in a transportation problem in order to solve it by the transportation algorithm.

Answer 2

False

Question 3

The total supply must be less than total demand in a transportation problem in order to solve it by the transportation algorithm.

Answer 3

False

Question 4

The total supply must be greater than total demand in a transportation problem in order to solve it by the transportation algorithm.

Question 5

In a transportation problem, if the total supply is greater than total demand, all constraints in its formulation can be written as equality constraints.

Question 6

In a transportation problem, if the total supply is equal to total demand, all constraints in its formulation can be written as equality constraints.

Question 7

The linear programming formulation of a transportation problem, in general, has demand constraints which are either $\geq$ or $=$ type.

Question 8

The linear programming formulation of a transportation problem, in general, has supply constraints which are either $\geq$ or $=$ type.

Question 9

Scheduling production in different time periods of a planning horizon can be formulated as a transportation problem.

Question 10

Transportation problem formulation can be used to help make location decisions when the total transportation cost is significant.

Question 11

Transportation problem formulation can be used to solve traffic congestion coming out of a ballpark at the end of a ball game.

Question 12

XYZ Inc. manufactures desks and chairs in all its four furniture manufacturing plants. It has 5 warehouses across the country. One transportation problem can be used to determine how to ship desks and chairs.

Question 13

In a linear programming formulation of the transshipment problem, if the total supply equals total demand, then all constraints could just be equality constraints.

Question 14

In a linear programming formulation of the transshipment problem, if the total supply is greater than the total demand, then all constraints could just be $\geq$ type constraints.

Question 15

A transshipment problem can be solved using the transportation formulation, as long as we are assured that no material stays in the intermediate points permanently.

Question 16

The transshipment problem formulation may be used in place of transportation formulation when there are two products that are being shipped, each having its own per unit cost of shipping.

Question 17

In a linear programming formulation of the assignment problem, the RHS of all constraints is greater than 1.

Question 18

In a linear programming formulation of the assignment problem, the RHS of all constraints is equal to 1.

Question 19

The number of possible assignments in an assignment problem with 4 jobs and 4 workers to assign them to would be 16.

Question 20

An assignment problem with 6 projects and 7 potential managers who can handle each of the projects, though with differing efficiency, cannot be solved since we would not know which manager to omit from assignment.

Question 21

An assignment problem with 6 projects and 7 potential managers who can handle each of the projects, though with differing efficiency, can be solved by adding a dummy project.

Question 22

An assignment problem with 6 projects and 7 potential managers who can handle each of the projects, though with differing efficiency, can be solved by adding a dummy manager.

Question 23

In a transportation problem with 5 supply points, 3 demand points, and total supply equaling total demand, the number of decision variables will be

A) 5
B) 8
C) 15
D) 125

Question 24

In a transportation problem with 5 supply points, 3 demand points, and total supply greater than total demand, the number of decision variables will be

A) 5
B) 9
C) 15
D) 20

Question 25

In a transportation problem with 5 supply points, 3 demand points, and total supply less than total demand, the number of decision variables will be

A) 6
B) 9
C) 15
D) 18

Question 26

If one formulates a transportation problem with 5 supply points, 3 demand points, and total supply greater than total demand, as a linear programming problem, the number of constraints will be

A) 5
B) 8
C) 3
D) 15

Question 27

Using transportation problem formulation to help a location decision where there are two potential locations to choose from, one has to solve

A) 3
B) 2
C) 1
D) several transportation problems.

Question 28

In the transportation problem model for production planning discussed in your text, if there are 3 periods and 4 methods of manufacturing in each period, how many rows will be needed?

A) 12
B) 7
C) 13
D) 8

Question 29

In the transportation problem model for production planning discussed in your text, if there are 3 periods and 4 methods of manufacturing in each period, how many columns will be needed?

A) 3
B) 4
C) 5
D) 8

Question 30

In the linear programming formulation of the transportation problem, cost of transporting one unit of the material from a supply point to a demand point appears in

A) the objective function only
B) the constraints only
C) both objective function and constraints
D) neither objective function nor constraints

Question 31

Data on cost, demand, and supply for a balanced (total supply equals total demand) transportation problem is given in the table below. In the linear programming formulation of this transportation problem with $\mathrm{X}_{i j}$ denoting the amount shipped from supply point $i$ (1 or 2 ) to demand point $j(1,2$ , or 3 ), the correct constraint to make sure that supply available in supply point \# 2 will be fully used is

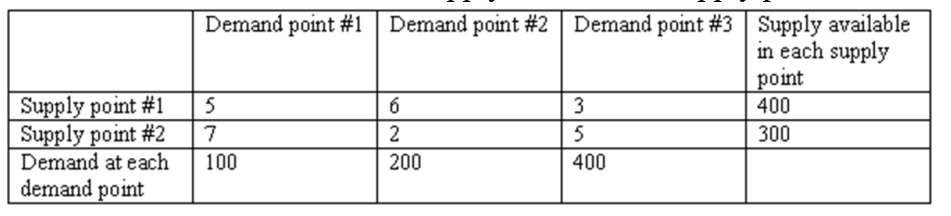
A) $7 X_{21}+2 X_{22}+5 X_{23}=300$
B) $X_{21}+X_{22}+X_{23}=300$
C) $7 X_{21}+2 X_{22}+5 X_{23} \geq 300$
D) $X_{21}+X_{22}+X_{23} \geq 300$

Question 32

Data on cost, demand, and supply for a balanced (total supply equals total demand) transportation problem is given in the table below. In the linear programming formulation of this transportation problem with $\mathrm{X}_{i j}$ denoting the amount shipped from supply point $i$ (1 or 2 ) to demand point $j(1,2$ , or 3 ), the correct constraint to make sure that demand in demand point 1 is fully met is

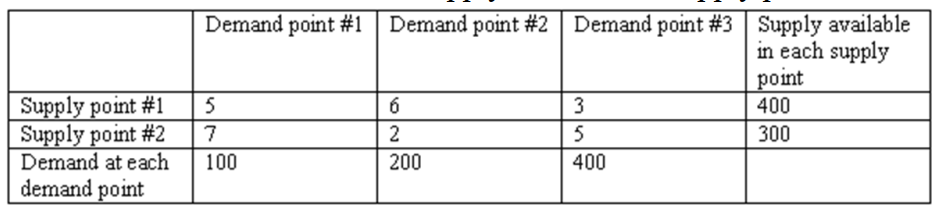
A) $5 X_{11}+7 X_{21}=100$
B) $X_{11}+X_{21} \leq 100$
C) $5 X_{11}+7 X_{21} \leq 100$
D) $X_{11}+X_{21}=100$

Question 33

Data on cost, demand and supply for a balanced (total supply equals total demand) transportation problem is given in the table below. In the linear programming formulation of this transportation problem with $\mathrm{X}_{i j}$ denoting the amount shipped from supply point $i$ (1 or 2 $)$ to demand point $j(1,2$ , or 3 $)$ , the correct constraint to make sure that demand in demand point 1 is fully met is

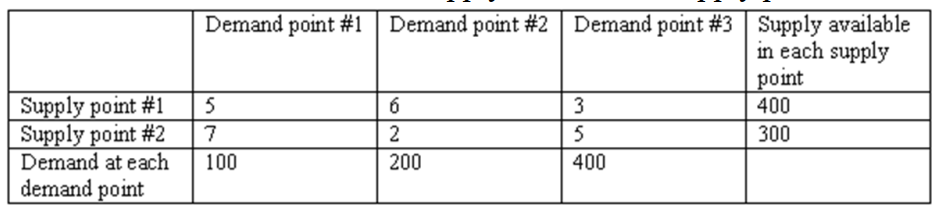
A) $5 X_{11}+7 X_{21}=100$
B) $X_{11}+X_{21} \leq 100$
C) $5 X_{11}+7 X_{21} \leq 100$
D) $X_{11}+X_{21}=100$

Question 34

Data on cost, demand, and supply for a balanced (total supply equals total demand) transportation problem is given in the table below. In the linear programming formulation of this transportation problem with $\mathrm{X}_{i j}$ denoting the amount shipped from supply point $i$ ( 1 or 2 ) to demand point $j(1,2$ or 3 ), the correct objective function is

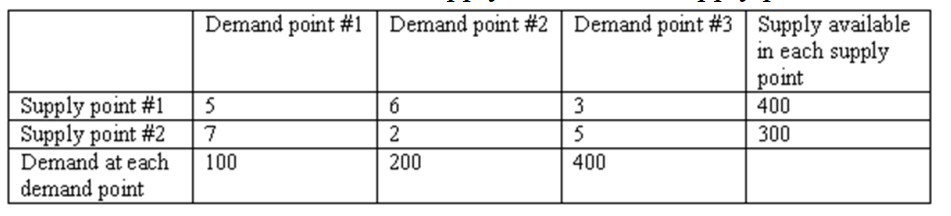
A) $\operatorname{Max}: 5 X_{11}+6 X_{12}+3 X_{13}+7 X_{21}+2 X_{22}+5 X_{23}$
B) $\operatorname{Min}: 5 X_{11}+6 X_{12}+3 X_{13}+7 X_{21}+2 X_{22}+5 X_{23}$
C) $\operatorname{Max}: X_{11}+X_{12}+X_{13}+X_{21}+X_{22}+X_{23}$
D) $\operatorname{Min}: X_{11}+X_{12}+X_{13}+X_{21}+X_{22}+X_{23}$

Question 35

In a transportation problem with total demand equal to 1200 and total supply equal to 900 , we should add a with a quantity equal to to convert it to a balanced problem.

A) dummy supply, 300
B) dummy supply, 2100
C) dummy demand, 300
D) dummy demand, 2100

Question 36

In a transportation problem with total demand equal to 900 and total supply equal to 1200 , we should add a with a quantity equal to to convert it to a balanced problem.

A) dummy supply, 300
B) dummy supply , 2100
C) dummy demand, 300
D) dummy demand, 2100

Question 37

In a transportation problem with total demand equal to 900 and total supply equal to 1200 , the cost associated with all dummy cells will be

A) 0
B) equal
C) a very large positive number
D) equal and it could be any numerical value

Question 38

In a transportation problem, if supply point 2 cannot ship to demand point 3 , all other things remaining the same as a regular transportation problem, the problem

A) cannot be solved
B) can be solved by letting the cost from supply point 2 to demand point 3 to be 0
C) can be solved by letting the cost from supply point 2 to demand point 3 to be a very high number
D) can be solved by removing supply point 2 from the problem and leaving all other things the same

Question 39

Which one of the following is not a required assumption in the formulation of transportation problems as a linear program?

A) Total supply equals total demand
B) Material transported is homogeneous
C) Per unit transportation cost from an origin to destination is constant
D) Total transportation cost from an origin to destination linearly increases with quantity shipped

Question 40

In a transshipment problem the intermediate points are treated as

A) additional origins
B) additional destinations
C) both origins and destinations
D) neither origins nor destinations

Question 41

In order to solve a transshipment problem, the number of intermediate points

A) must be less than the number of origins
B) must be less than the number of destinations
C) must be less than both the number of origins and destinations
D) can be any number and is not related to number of origins or destinations

Question 42

In the linear programming formulation of the transshipment problem, there are a set of constraints that require the total shipment to each intermediate point be the total shipment out of each intermediate point.

A) greater than
B) less than
C) equal to
D) unequal to

Question 43

In the linear programming formulation of the transshipment problem, demand at the destination points is required to be satisfied from shipment from

A) origins
B) intermediate points
C) either origins or intermediated points
D) origins or external sources

Question 44

A transshipment problem has 3 origins, 2 intermediate points, and 4 destinations. The number of constraints in the linear programming formulation crafted from the principles discussed in the text will be

A) 7
B) 9
C) 5
D) 14

Question 45

A transshipment problem has 3 origins, 4 intermediate points, and 2 destinations. In the linear programming formulation, using the principles discussed in the text, the number of constraints with 0 on the RHS will be

A) 3
B) 2
C) 7
D) 4

Question 46

The number of possible assignments in an assignment problem with 6 jobs and 6 workers to assign them to would be

A) 36
B) 12
C) 120
D) 720

Question 47

The number of constraints in the standard linear programming formulation of a 6 worker- 6 jobs assignment problem using the approach presented in the text will be

A) 12
B) 36
C) 120
D) 720

Question 48

Using the approach presented in the text, the number of decision variables required for formulation of an assignment problem with 6 jobs and 6 workers will be

A) 36
B) 12
C) 120
D) 720

Question 49

In an assignment problem, suppose we have 5 projects and a potential list of 6 managers who could be the project manager for any one of the projects. The problem can be formulated by adding a thus converting it to a standard assignment problem.

A) dummy project
B) dummy manager
C) dummy cost
D) dummy utility

Question 50

Coast to Central Plains Inc. has warehouses in Piscataway, San Francisco, and Miami. It supplies the demand at four distribution centers in Austin, Lafayette, Toledo, and Knoxville from these warehouses. Data on cost, demand, and supply are given in the table below. Solve this using excel and report the optimal solution and the total cost corresponding to the optimal solution.

Question 51

Coast to Central Plains Inc. has warehouses in Piscataway, San Francisco, and Miami. It supplies the demand at four distribution centers in Austin, Lafayette, Toledo, and Knoxville from these warehouses. Data on cost, demand, and supply are given in the table below. Solve this using excel and report the optimal solution and the total cost corresponding to the optimal solution.

Question 52

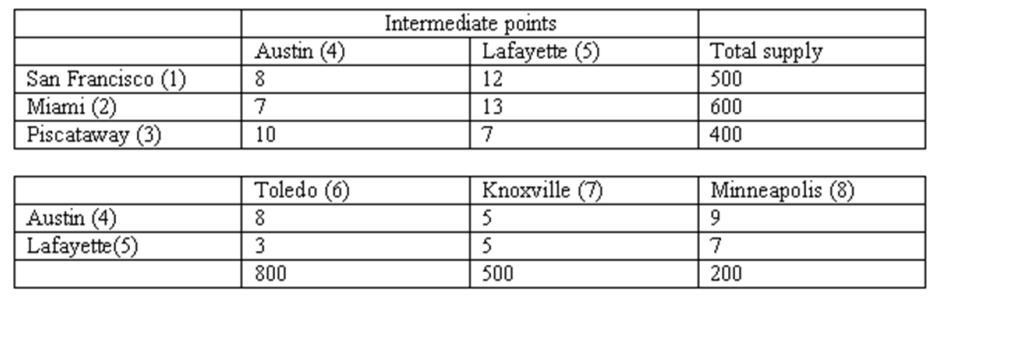
Carlos Ginsburg, a manger at Transship Inc., recently returned from a seminar on transshipment type problems. He wanted to cast his company's shipping plan into a transshipment problem. Formulate the problem and help Carlos get his promotion.

Question 53

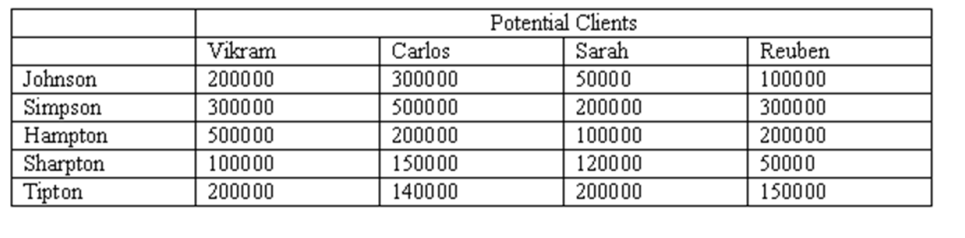
Phil Chandler Insurance Agency has 4 potential clients to allocate among 5 salesmen. The expected sales for each salesman-client allocation is given in the following table. Using the assignment model, find the best assignment of salesman to client.