Deck 8: Network Optimization Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/61
Play
Full screen (f)
Deck 8: Network Optimization Models
1
Network models are important because of their application potential and ease of solution procedures.
True
2
In the shortest route problem, nodes represent locations, and arcs represent the distance between locations.
True
3
In the shortest route problem, the temporary label on the node closest to the destination is converted to a permanent label.
False
4
In the shortest route problem, the objective is to find the shortest route from an origin to a destination through a network.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
5
In the shortest route problem, backtracking is used as a feasibility check on a network solution.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
6
The shortest path algorithm given in the text will work even if the costs (distances) of the arcs are negative.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
7
The objective in a minimal spanning tree problem is to find the least cost way of connecting all nodes to the origin or destination.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
8
The labels used in the algorithm to find the shortest path have two numbers, the first of which refers to the node that immediately precedes the current node in the path.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
9
The symbol in the labeling algorithm for shortest path represents stationary node.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
10
[ ] in the labels of the shortest path algorithm given in the text indicates that the node has having a permanent label.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
11
In the shortest path algorithm given in the text, all nodes will have a label either temporary or permanent, even at the starting point.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
12
In the shortest path algorithm given in the text, when the procedure is completed, the shortest paths from starting node to all other nodes have been found.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
13
In solving the shortest path problem by using a linear programming formulation and excel, we add a very high (dummy) cost corresponding to all non-existing arcs so that they will not be in the solution.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
14
In the linear programming formulation of the shortest path problem, the constraint corresponding to the origin will have 1 on its RHS.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
15
Flow conservation is assumed in the spanning tree problem.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
16
In finding the minimal spanning tree in a network using the algorithm in the text, if a tie occurs in the shortest arc from connected nodes to a node that is not connected, it may not be broken arbitrarily.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
17
The solution to a minimum spanning tree problem over a network of pipes gives you the total amount of material that can be piped from the origin to the destination.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
18
If cost per foot length of pipe is , the minimal total cost of connecting all nodes of a network with this piping is given by the total value of the minimum spanning tree .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
19
Greedy algorithm finds the optimal solution in the minimal spanning tree problem.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
20
In the spanning tree algorithm, we try to find the shortest arc from the connected nodes to any nodes of the rest of the graph.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
21
In the spanning tree algorithm, suppose that nodes 1,2 , and 3 are in the connected component at some point in the algorithm; this implies that all arcs between nodes 1,2 , and 3 , if they exist, will have to be in the connected component.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
22
In the spanning tree problem, one is trying to find the longest tree from the origin to the destination.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
23
In the minimal spanning tree algorithm given in the text, the length of the spanning tree will differ depending upon the starting node used in the algorithm.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
24
In the minimal spanning tree algorithm given in the text, the final result, that is the minimum spanning tree, can best be described by the nodes in the minimal spanning tree.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
25
In the minimal spanning tree algorithm given in the text, the algorithm is finished and a solution is found when all arcs have been included in the minimal spanning tree.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
26
In the shortest route problem, the algorithm will find all shortest paths from any node to any node.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
27
In the shortest route problem, the algorithm (the final result, that is, the shortest path found from origin to destination) can best be described by the nodes on the shortest path in the order in which they should be traversed to get from origin to destination.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
28
In the shortest route problem, the length of the shortest path will depend on the origin destination pair used in the algorithm.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
29
Using the data on a network of oil pipelines from Baku in Azerbaijan to a refinery in Turkey, if we solve the network flow problem with Baku as the source node and the Turkish refinery as the sink node, using the shortest route problem, the algorithm will find all shortest paths from any node to any node.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
30
In the iterations of the maximal flow algorithm, the sum of the capacity/flow values of at each end of an arc is always equal to the sum of the original capacity values at each end of the arc.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
31
In flows in network, the optimal solution to the maximal flow problem cannot have simultaneous flows in both directions of an arc.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
32
The maximum flow in a network will always be equal to the minimum of the minimum of the total capacity of the branches leaving the source or entering the sink.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
33
The maximum flow in a network will always be less than or equal to the minimum of the minimum of the total capacity of the branches leaving the source or entering the sink.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
34
Assume that you are a logistics manager for a firm in Toledo, Ohio. Your products should reach New York city. There are many ways to reach New York city from Toledo. If total time is strictly proportional to total distance, in order to send your products as quickly as possible, you would like to model your problem as
A)maximal flow problem
B) minimal spanning tree problem
C) shortest path problem
D) shortest path in a spanning tree problem
A)maximal flow problem
B) minimal spanning tree problem
C) shortest path problem
D) shortest path in a spanning tree problem

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
35
What is not true in the shortest path algorithm discussed in the textbook?
A) Permanent node labels in the shortest path algorithm will always be permanent
B) Temporary node labels are indicated by ()
C) Values of distances in the temporary node labels will not change
D) Values of distances in the permanent node labels will not change
A) Permanent node labels in the shortest path algorithm will always be permanent
B) Temporary node labels are indicated by ()
C) Values of distances in the temporary node labels will not change
D) Values of distances in the permanent node labels will not change

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
36
What is not true in the shortest path algorithm discussed in the textbook?
A) Permanent node labels in the shortest path algorithm are indicated by [ ]
B) The second number in the temporary node label denotes distance
C) The smallest in the algorithm refers only to distance and not node number
D) Values of distances in the permanent node labels will not change
A) Permanent node labels in the shortest path algorithm are indicated by [ ]
B) The second number in the temporary node label denotes distance
C) The smallest in the algorithm refers only to distance and not node number
D) Values of distances in the permanent node labels will not change

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
37
In the shortest route algorithm discussed in the textbook, backtracking means
A) going back on your calculations and revising it
B) solving the problem again using destination as the origin and vice-versa
C) process that identifies the shortest path, starting it from the origin
D) process that identifies the shortest path starting with the destination and working backward toward the origin
A) going back on your calculations and revising it
B) solving the problem again using destination as the origin and vice-versa
C) process that identifies the shortest path, starting it from the origin
D) process that identifies the shortest path starting with the destination and working backward toward the origin

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
38
Which is not a reason for the importance of network models as a problem solving tool of management science?
A)They are usually easier to analyze
B) They can be solved by two methods, geometrically and analytically
C) They apply to abroad range of problems
D) Visual presentation makes the results intuitive
A)They are usually easier to analyze
B) They can be solved by two methods, geometrically and analytically
C) They apply to abroad range of problems
D) Visual presentation makes the results intuitive

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
39
The arcs in the shortest path problem represent
A) quantities that can be shipped
B) direction of shipping
C) flow rate capacity
D) travel time from node to node
A) quantities that can be shipped
B) direction of shipping
C) flow rate capacity
D) travel time from node to node

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
40
Minimal spanning tree problem can be applied to find
A)minimum distance between nodes
B) minimum length to connect all the nodes
C) maximal flow in a network
D) minimal capacity of a network
A)minimum distance between nodes
B) minimum length to connect all the nodes
C) maximal flow in a network
D) minimal capacity of a network

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
41
In a minimal spanning tree solution, which of the following is not true?
A) If you add one more arc to it, it will no longer be a minimal spanning tree
B) If you remove an arc, it will no longer be a spanning tree
C) You can find the shortest route by picking from the minimum spanning tree judiciously
D) There may be alternate minimal spanning trees in a problem
A) If you add one more arc to it, it will no longer be a minimal spanning tree
B) If you remove an arc, it will no longer be a spanning tree
C) You can find the shortest route by picking from the minimum spanning tree judiciously
D) There may be alternate minimal spanning trees in a problem

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
42
Shortest round trip distances from origin to destination using shortest route problem is (mark what is true)
A) difficult to find
B) found by using the algorithm another time reversing the origin and destination
C) simply double the shortest route
D) the sum of two distinct paths-one from origin to destination and the other, reverse
A) difficult to find
B) found by using the algorithm another time reversing the origin and destination
C) simply double the shortest route
D) the sum of two distinct paths-one from origin to destination and the other, reverse

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
43
Consider a path 1-2-4-6, in a network where 1 is the source and 6 is the sink. Suppose that the capacity in this direction from 1-2 is 5, 2-4 is 7, and 4-6 is 3 , then the flow capacity of this path in the direction given above will be
A) 5
B) 7
C) 3
D) 15
A) 5
B) 7
C) 3
D) 15

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
44
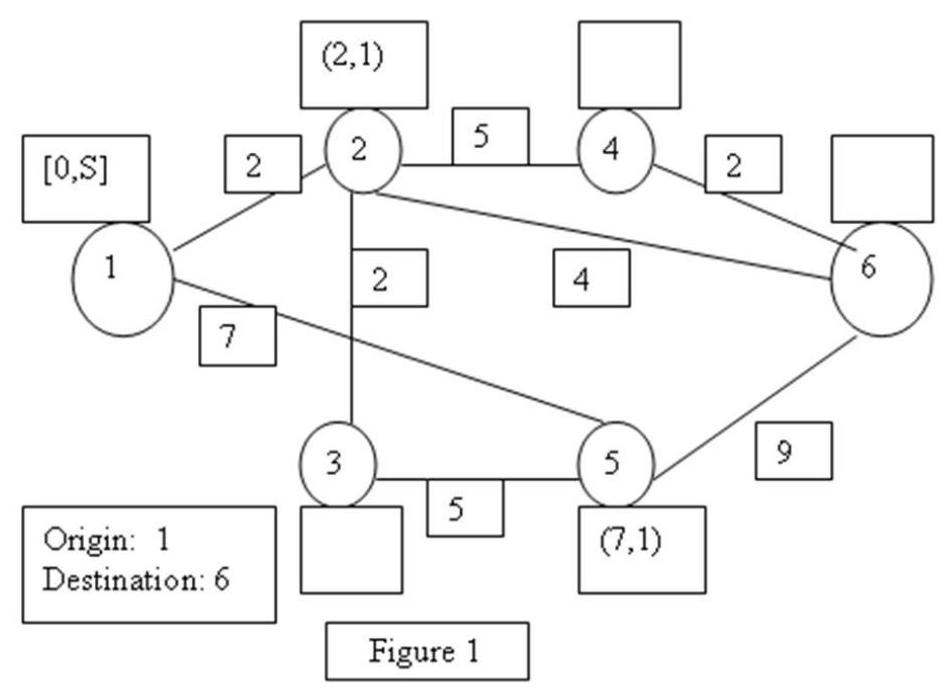
-In Figure 1, using the shortest route algorithm presented in the text book, the node that would be labeled with a permanent label next will be
A)1
B) 2
C) 3
D) 5

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
45

-In Figure 1, using the shortest route algorithm presented in the text book, the shortest path from node 1 to node 6 is
A) 6
B) 9
C) 18
D) 5

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
46
![<strong> -In Figure 2a, using the shortest route algorithm presented in the text book, the label and the node that would get the permanent label next, will be </strong> A)3 and [5,2] B) 4 and [8,2] C) 5 and [7,1] D) 2and [3,1]](https://storage.examlex.com/TB10310/11ee8b96_7ba1_f195_b323_3bbe86f1ca58_TB10310_00.jpg)
-In Figure 2a, using the shortest route algorithm presented in the text book, the label and the node that would get the permanent label next, will be
A)3 and
B) 4 and
C) 5 and
D) 2and

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
47
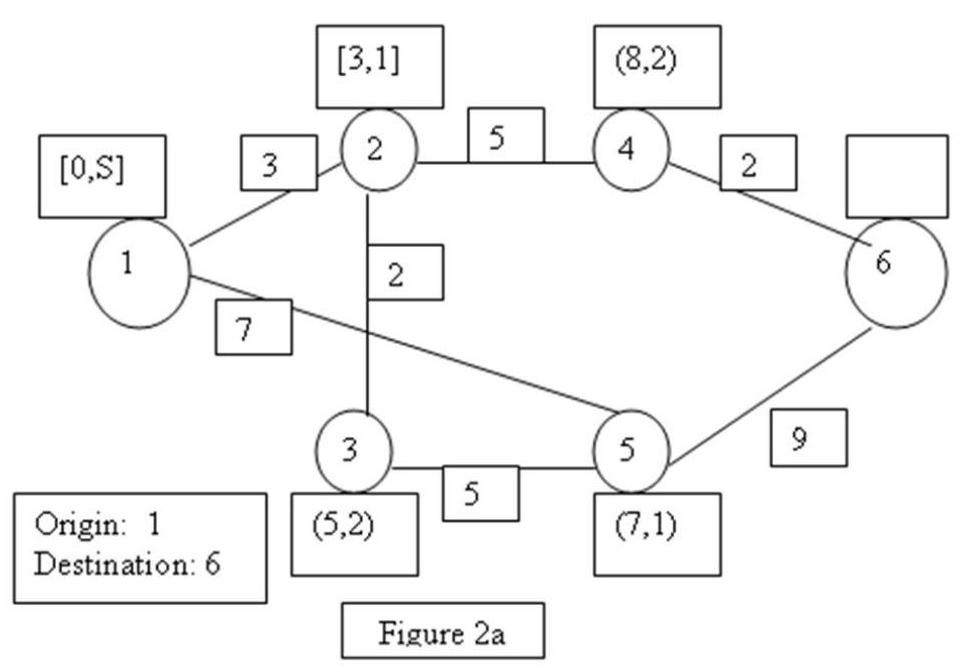
-In Figure 2a, using the shortest route algorithm presented in the text book, the shortest distance from node 1 to node 6 will be
A) 16
B) 10
C) 19
D) 6

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
48
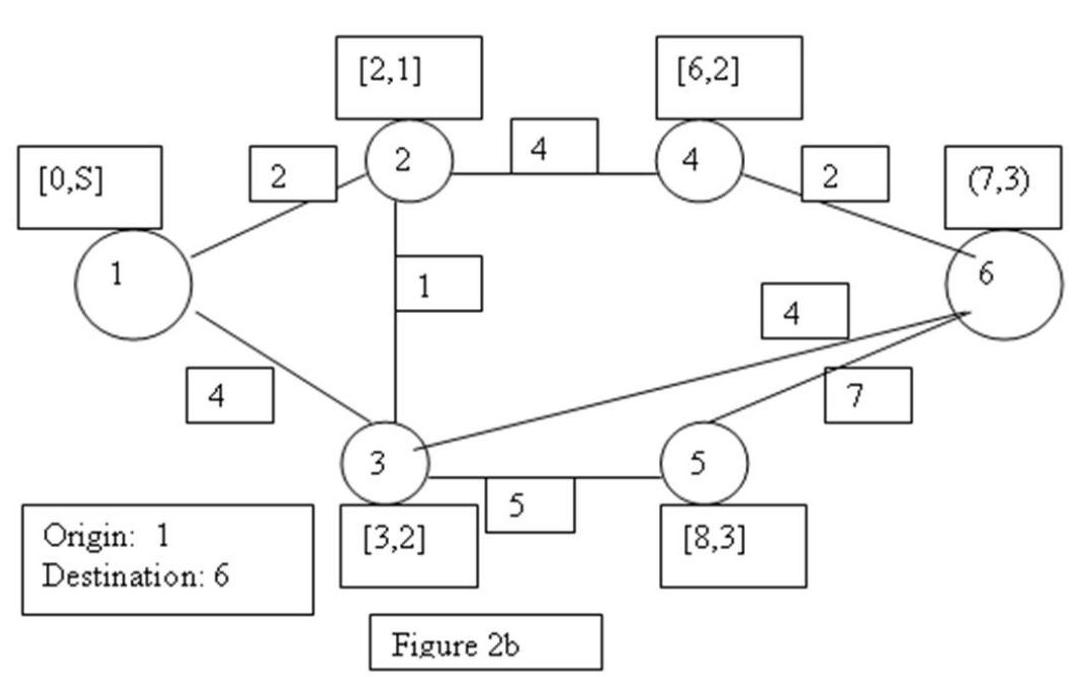
-In Figure 2b, using backtracking step of the shortest route algorithm, the shortest route from node 1 to node 6 is
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
49

-In Figure 2b, using backtracking step of the shortest route algorithm, the shortest route from node 1 to node 3 is
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
50
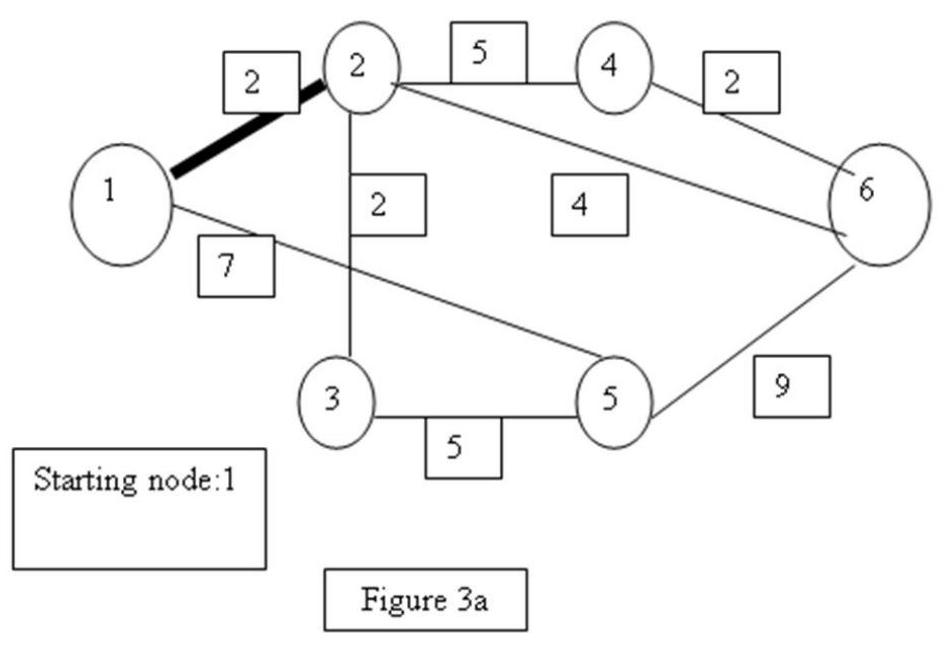
-In Figure 3a, bold arc and all nodes attached to it is the connected node. Using the algorithm in the text for finding the minimal spanning tree, which will be the next node added to the set of connected nodes?
A) 3
B) 6
C) 4
D) 5

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
51

-What is the total distance corresponding to the minimal spanning tree of Figure 3a?
A) 25
B) 12
C) 15
D) 24

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
52
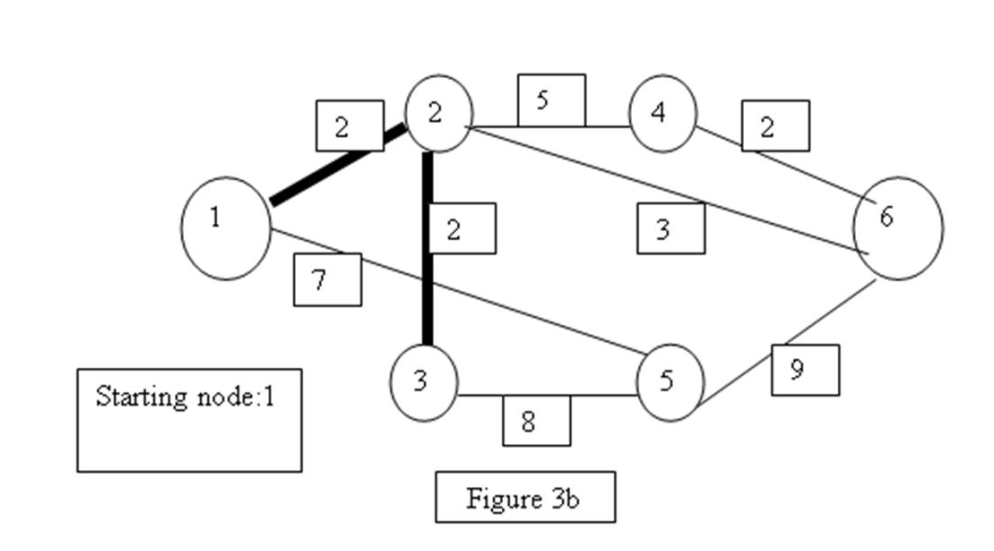
-In Figure 3b, thick solid arcs correspond to arc that have been already chosen using the minimum spanning tree algorithm. What will be the next node that will be selected as per the algorithm?
A) 4
B) 3
C) 5
D) 6

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
53

-In Figure 3b, what is the length of the minimum spanning tree using the algorithm presented in the text and continuing to add nodes to the connected components shown by thick arcs?
A)16
B) 17
C) 12
D) 26

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
54

-In Figure 3b, what are the arcs in the minimal spanning tree found by using the minimum spanning tree algorithm presented in the text?
A) 16
B) 17
C) 12
D) 26

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose that you are applying the minimal spanning tree algorithm. At some point during the application, you have a connected component. Which one of the following is true?
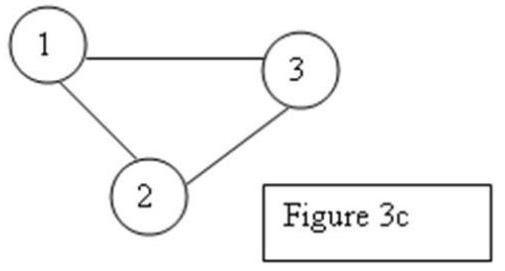
A) Your connected component can look like Figure 3c.
B) Connected components have only nodes.
C) Connected components have only arcs.
D)Connected component cannot be looking like Figure 3c, since 3 nodes will have only 2 arcs between in the connected component.

A) Your connected component can look like Figure 3c.
B) Connected components have only nodes.
C) Connected components have only arcs.
D)Connected component cannot be looking like Figure 3c, since 3 nodes will have only 2 arcs between in the connected component.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose that you are applying the maximal flow algorithm. At some point during the application, you have an arc with the numbers 6 and 3 as shown above in Figure 3d. Which of the following is incorrect?
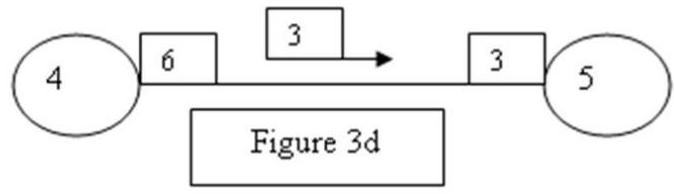
A) The flow from 4 to 6 can be increased by up to 6 units
B) The original numbers at the end of the arcs must add up to 9
C) A flow of 3 units can go from 5 to 4
D) An additional flow of 9 units can go from 4 to 6

A) The flow from 4 to 6 can be increased by up to 6 units
B) The original numbers at the end of the arcs must add up to 9
C) A flow of 3 units can go from 5 to 4
D) An additional flow of 9 units can go from 4 to 6

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
57
What is the maximum flow possible from source to sink in the network given in Figure 4a?
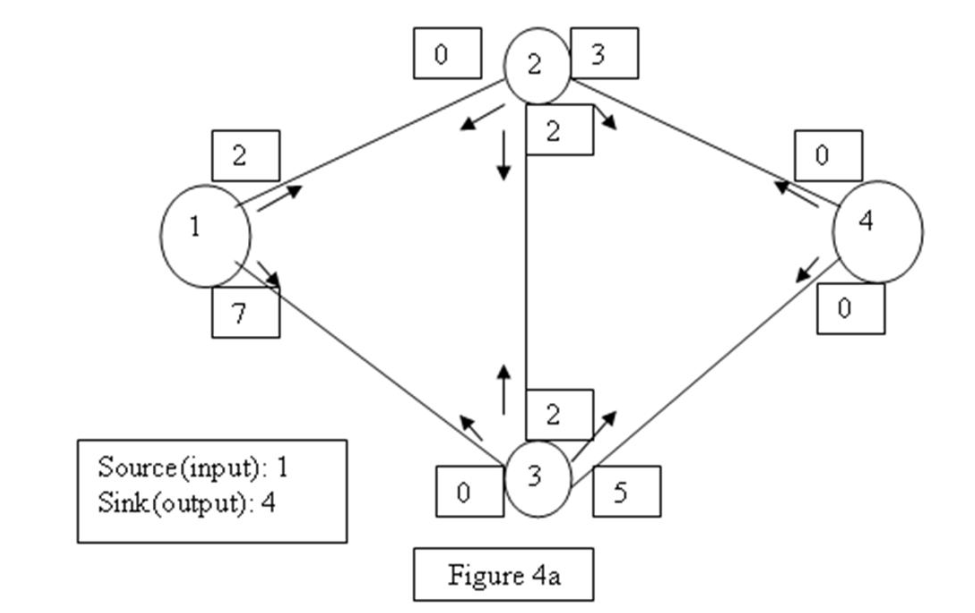
A) 9
B) 8
C) 7
D) 10

A) 9
B) 8
C) 7
D) 10

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
58
What is the maximum flow possible from source to sink in the network given in Figure 4b?
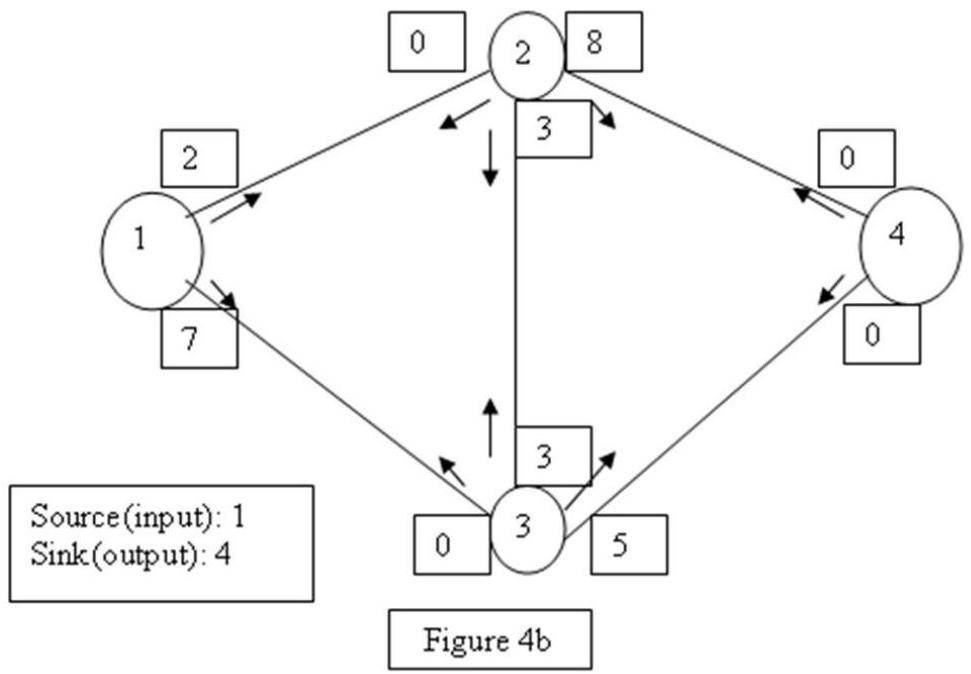
A) 9
B) 13
C) 7
D) 10

A) 9
B) 13
C) 7
D) 10

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
59
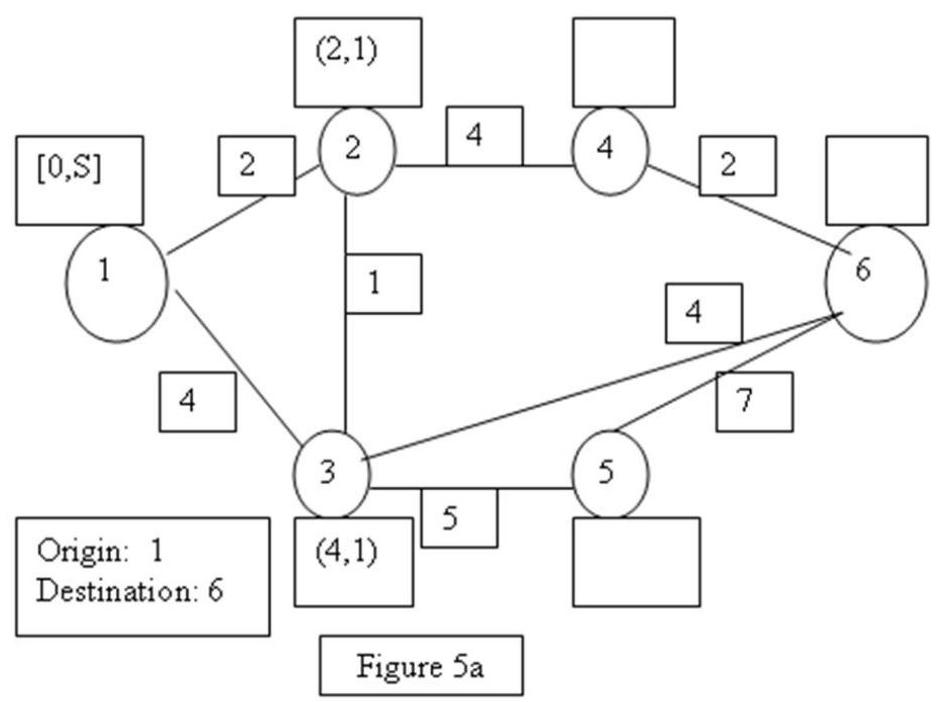
Find the shortest route from node 1 to all other nodes of the graph using the shortest route algorithm given in the book. List all the shortest routes in a table.


Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
60
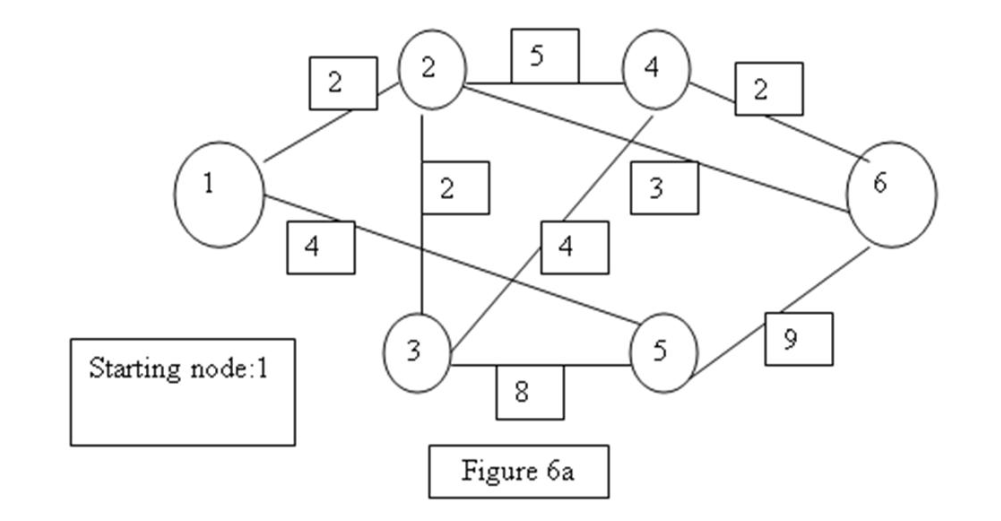
Find the minimal spanning tree of the network given in Figure 6a.


Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
61
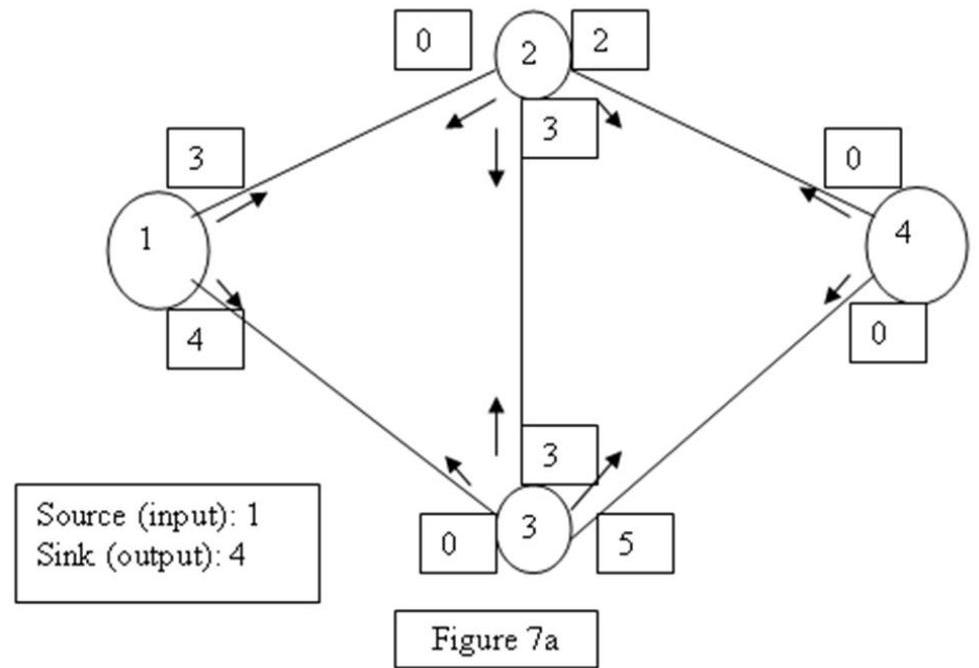
Find the maximal flow in the network given in Figure 7a.


Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck


