Deck 13: Voting: You Cant Always Get What You Want
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/69
Play
Full screen (f)
Deck 13: Voting: You Cant Always Get What You Want
1
A voting procedure in which the alternative that receives the most votes wins, even if that alternative does not receive a majority of the votes, is known as the
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
plurality-rule method
2
A voting procedure in which the winner must defeat each of the other alternatives in head-to-head contests is known as the
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
Condorcet method.
3
A voting procedure in which each voter ranks alternatives and awards more points to higher-ranked alternatives and fewer points to lower-ranked alternatives, and the alternative which receives the most total points from all voters wins, is known as the
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
Borda-count method.
4
A voting procedure in which voters initially rank alternatives, the alternative with the fewest first-place votes is eliminated and those votes are transferred to each voter's next-favorite choice, and the process repeats until a winner emerges, is known as the
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method
A) Borda-count method.
B) Condorcet method.
C) instant runoff method.
D) plurality-rule method

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
5
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. If the voting method used to select a location for the recreation center is the plurality-rule method, the recreation center will be built in
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. If the voting method used to select a location for the recreation center is the plurality-rule method, the recreation center will be built in
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
6
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. If the voting method used to select a location for the recreation center is the plurality-rule method, the number of voters who will vote against the winning city is
A) 135.
B) 195.
C) 255.
D) 405.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. If the voting method used to select a location for the recreation center is the plurality-rule method, the number of voters who will vote against the winning city is
A) 135.
B) 195.
C) 255.
D) 405.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
7
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. The winner of that vote will receive ________ votes.
A) 150
B) 285
C) 405
D) 480
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. The winner of that vote will receive ________ votes.
A) 150
B) 285
C) 405
D) 480

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
8
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. In the second round of voting, the winner of the first round will go up against Desert Sands. The winner of the second-round vote will receive ________ votes.
A) 285
B) 345
C) 405
D) 455
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. In the second round of voting, the winner of the first round will go up against Desert Sands. The winner of the second-round vote will receive ________ votes.
A) 285
B) 345
C) 405
D) 455

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
9
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. In the second round of voting, the winner of the first round will go up against Desert Sands. In the third round of voting, the winner of the second round will go up against Oceanside. The winner of the third-round vote will receive ________ votes.
A) 285
B) 345
C) 405
D) 455
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. In the second round of voting, the winner of the first round will go up against Desert Sands. In the third round of voting, the winner of the second round will go up against Oceanside. The winner of the third-round vote will receive ________ votes.
A) 285
B) 345
C) 405
D) 455

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
10
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. The winner of that vote will go up against Desert Sands, and the winner of this vote will finally go up against Oceanside. In this scenario, the Condorcet winner will be
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Condorcet method. In the first round of voting, the residents of the 4 towns can choose between Glacier Cove and Mountain View. The winner of that vote will go up against Desert Sands, and the winner of this vote will finally go up against Oceanside. In this scenario, the Condorcet winner will be
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
11
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points, a town ranked 2 gets 2 points, a town ranked 3 gets 1 point, and a town ranked 4 gets no points. With this method, the town that gets the least number of points is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points, a town ranked 2 gets 2 points, a town ranked 3 gets 1 point, and a town ranked 4 gets no points. With this method, the town that gets the least number of points is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
12
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, the town that gets the greatest number of points is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, the town that gets the greatest number of points is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
13
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, Desert Sands receives ________ points.
A) 585
B) 795
C) 1095
D) 1125
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, Desert Sands receives ________ points.
A) 585
B) 795
C) 1095
D) 1125

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
14
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, Mountain View receives ________ points.
A) 585
B) 795
C) 1095
D) 1125
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method, where if a town gets ranked 1, it gets 3 points per vote, a town ranked 2 gets 2 points per vote, a town ranked 3 gets 1 point per vote, and a town ranked 4 gets no points per vote. With this method, Mountain View receives ________ points.
A) 585
B) 795
C) 1095
D) 1125

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
15
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method. The residents of Desert Sands, realizing that they have no chance of winning this election, decide to remove their town from contention, so now with only 3 towns in the running, if a town gets ranked 1, it gets 2 points per vote, a town ranked 2 gets 1 point per vote, and a town ranked 3 gets no points per vote. With this method, the town that wins in this election is
A) There is no clear winner in this election.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the Borda-count method. The residents of Desert Sands, realizing that they have no chance of winning this election, decide to remove their town from contention, so now with only 3 towns in the running, if a town gets ranked 1, it gets 2 points per vote, a town ranked 2 gets 1 point per vote, and a town ranked 3 gets no points per vote. With this method, the town that wins in this election is
A) There is no clear winner in this election.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
16
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the first town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the first town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
17
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the second town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the second town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
18
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the third town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the third town to be eliminated is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
19
Figure 13.1 :  A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the winner is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.
 A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.
A recreation center is to be built, which will serve the populations of 4 isolated towns in Atlas County. The residents of these 4 towns all agree that a recreation center is a much-needed asset, and every resident wants to live as close to the recreation center as possible. The only conflict is selecting the town in which the recreation center is to be built. Due to utility restrictions, the center needs to be built in one of these towns and not somewhere between any of the towns. A map showing the location of these towns, the voting populations of the towns, and the driving distance between the towns is shown in the above figure. Assume that everyone in the voting population casts a vote, and that the votes cast reflect everyone's desire to live as close as possible to the recreation center.-Refer to Figure 13.1. Assume the voting method used to select a location for the recreation center is the instant runoff method. With this method, each voter ranks the towns in order of preference, from first to fourth. The town with the fewest first-place votes will be eliminated, and anyone who voted for that town will have their first-place vote transferred to the town they liked next best. This process continues until only one town is left, and that town will be declared the winner. With this method, the winner is
A) Desert Sands.
B) Glacier Cove.
C) Mountain View.
D) Oceanside.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
20
In U.S. presidential elections, the winner of the popular vote
A) was always the election winner.
B) lost the election only one time in history.
C) lost the election about 10 percent of the time.
D) lost the election more times than he won the election.
A) was always the election winner.
B) lost the election only one time in history.
C) lost the election about 10 percent of the time.
D) lost the election more times than he won the election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
21
The idea that there is no voting system that can consistently make a fair choice among three or more candidates is a conclusion of
A) Arrow's impossibility theorem.
B) the Condorcet paradox.
C) the Voting Rights Act of 1965.
D) the median voter theorem.
A) Arrow's impossibility theorem.
B) the Condorcet paradox.
C) the Voting Rights Act of 1965.
D) the median voter theorem.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
22
When there are three or more options, plurality-rule voting does a good job of capturing the preferences of voters.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
23
The Condorcet paradox shows that even if each individual in a group has transitive preferences, the group's collective preferences may not be transitive.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
24
When the Condorcet system of voting is used, there is always a Condorcet winner.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
25
In the Borda-count voting method, irrelevant alternatives are never an issue.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
26
The instant runoff voting method is also known as a single transferrable vote system.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
27
According to Arrow's impossibility theorem, all voting systems contain some inherent drawback that may prevent them from accurately capturing the preferences of the electorate in all circumstances.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
28
When each member of a group has transitive preferences but the collective preferences of the group are not transitive, this is an anomaly known as the ________.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
29
When the ________ system of voting is used, each voter ranks alternatives and awards more points to higher-ranked alternatives and fewer points to lower-ranked alternatives. The alternative that receives the most total points from all voters wins.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
30
Four candidates are running for president of their book club, which has a total of 36 members. The table below indicates the number of voters and their preferences. Determine the winner under the Condorcet method with the following rules:
a. In the first round of voting, Amy goes up against Byron. In the second round, the first-round winner goes up against Coco, and in the final round, the second-round winner goes up against Dinesh.
b. In the first round of voting, Byron goes up against Dinesh. In the second round, the first-round winner goes up against Coco, and in the final round, the second-round winner goes up against Amy.
c. In the first round of voting, Dinesh goes up against Coco. In the second round, the first-round winner goes up against Amy, and in the final round, the second-round winner goes up against Byron.
d. Based on the above three voting scenarios, is there a Condorcet winner for this election?
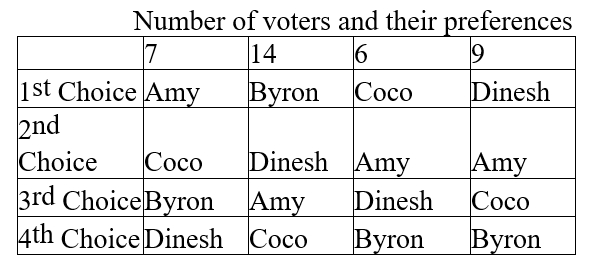
a. In the first round of voting, Amy goes up against Byron. In the second round, the first-round winner goes up against Coco, and in the final round, the second-round winner goes up against Dinesh.
b. In the first round of voting, Byron goes up against Dinesh. In the second round, the first-round winner goes up against Coco, and in the final round, the second-round winner goes up against Amy.
c. In the first round of voting, Dinesh goes up against Coco. In the second round, the first-round winner goes up against Amy, and in the final round, the second-round winner goes up against Byron.
d. Based on the above three voting scenarios, is there a Condorcet winner for this election?


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
31
Four candidates are running for president of their book club, which has a total of 36 members. The table below indicates the number of voters and their preferences. Determine the winner under the plurality-rule method, the Borda-count method (assigning 3 points to each first choice, 2 points to each second choice, 1 point to each third choice, and no points to each fourth choice), and the instant runoff method.
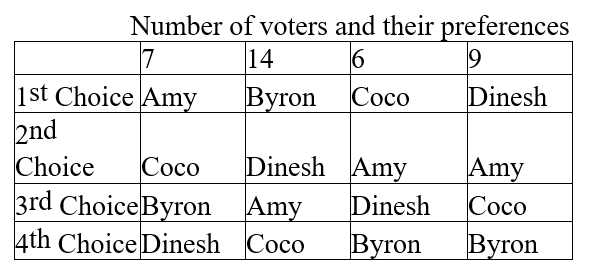


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
32
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. The technical name given to Alice, based on her position in the figure, is the
A) election moderator.
B) median voter.
C) irrelevant alternative.
D) strategic voter.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. The technical name given to Alice, based on her position in the figure, is the
A) election moderator.
B) median voter.
C) irrelevant alternative.
D) strategic voter.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
33
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, the winner of the election will be
A) Oliver Cousins.
B) George Glass.
C) The vote will end in a tie.
D) It is uncertain who will win this election.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, the winner of the election will be
A) Oliver Cousins.
B) George Glass.
C) The vote will end in a tie.
D) It is uncertain who will win this election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
34
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Oliver will definitely receive at least ________ votes and George will definitely receive at least ________ votes.
A) 4; 4
B) 4; 5
C) 5; 4
D) 5; 5
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Oliver will definitely receive at least ________ votes and George will definitely receive at least ________ votes.
A) 4; 4
B) 4; 5
C) 5; 4
D) 5; 5

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
35
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Alice's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Alice is indifferent between the two candidates.
D) Alice definitely does not like either candidate.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Alice's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Alice is indifferent between the two candidates.
D) Alice definitely does not like either candidate.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
36
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Cindy's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Cindy is indifferent between the two candidates.
D) Cindy definitely does not like either candidate.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Cindy's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Cindy is indifferent between the two candidates.
D) Cindy definitely does not like either candidate.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
37
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Bobby's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Bobby is indifferent between the two candidates.
D) Bobby definitely does not like either candidate.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If Oliver's political views place him at the L4 position and George's political views place him at the C4 position, Bobby's preference for mayor is
A) Oliver Cousins.
B) George Glass.
C) Bobby is indifferent between the two candidates.
D) Bobby definitely does not like either candidate.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
38
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. Assuming Oliver does not change his political views, George would receive the greatest number of votes if he altered his political views to place him at the ________ position.
A) M
B) C3
C) C1
D) L3
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. Assuming Oliver does not change his political views, George would receive the greatest number of votes if he altered his political views to place him at the ________ position.
A) M
B) C3
C) C1
D) L3

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
39
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. Assuming Oliver does not change his political views, George could alter his political views by the least amount and guarantee that he would win the election if he aligned himself with the political views represented by
A) Alice.
B) Greg.
C) Marcia.
D) Carol.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. Assuming Oliver does not change his political views, George could alter his political views by the least amount and guarantee that he would win the election if he aligned himself with the political views represented by
A) Alice.
B) Greg.
C) Marcia.
D) Carol.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
40
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George changed his political views to be more aligned with the views of Jan, Oliver could alter his political views by the least amount and guarantee that he would win the election if he aligned himself with the political views represented by
A) Alice.
B) Bobby.
C) Marcia.
D) Cindy.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George changed his political views to be more aligned with the views of Jan, Oliver could alter his political views by the least amount and guarantee that he would win the election if he aligned himself with the political views represented by
A) Alice.
B) Bobby.
C) Marcia.
D) Cindy.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
41
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, while Oliver does not change his political views, the winner of the election will be ________ with a winning vote total of ________.
A) Oliver Cousins; 6 votes
B) George Glass; 5 votes
C) Oliver Cousins; 5 votes
D) George Glass; 6 votes
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, while Oliver does not change his political views, the winner of the election will be ________ with a winning vote total of ________.
A) Oliver Cousins; 6 votes
B) George Glass; 5 votes
C) Oliver Cousins; 5 votes
D) George Glass; 6 votes

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
42
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position, the winner of the election will be ________ with a winning vote total of ________.
A) Oliver Cousins; 6 votes
B) George Glass; 5 votes
C) Oliver Cousins; 5 votes
D) George Glass; 6 votes
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. If George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position, the winner of the election will be ________ with a winning vote total of ________.
A) Oliver Cousins; 6 votes
B) George Glass; 5 votes
C) Oliver Cousins; 5 votes
D) George Glass; 6 votes

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
43
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position. In order for George to maintain as much of his conservative credentials as possible and still win the election, he would need to align himself with the political views represented by
A) Alice.
B) Cindy.
C) Bobby.
D) Jan.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position. In order for George to maintain as much of his conservative credentials as possible and still win the election, he would need to align himself with the political views represented by
A) Alice.
B) Cindy.
C) Bobby.
D) Jan.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
44
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position. George counters this statement by stating that in addition to taxes being raised, the government should provide free health care to all its citizens, which moves him to the C2 position. In order for Oliver to definitely win the election, he will need to
A) move farther to the right.
B) move farther to the left.
C) not move at all.
D) move exactly to the middle, for this is the only way he will win the election in this instance.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. George comes out with a statement supporting an increase in taxes on the rich, which moves him to the C3 position, and Oliver responds by not only stating that taxes should not be raised, but in fact should be lowered, moving him to the L2 position. George counters this statement by stating that in addition to taxes being raised, the government should provide free health care to all its citizens, which moves him to the C2 position. In order for Oliver to definitely win the election, he will need to
A) move farther to the right.
B) move farther to the left.
C) not move at all.
D) move exactly to the middle, for this is the only way he will win the election in this instance.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
45
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. The median voter theorem suggests that in an ordinary election such as that between Oliver and George, natural forces will drive these candidates to a situation where their political views each reflect the views of
A) Alice.
B) Mike.
C) Carol.
D) all of the voters.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views initially placed him at the L4 position and George's political views initially placed him at the C4 position. The median voter theorem suggests that in an ordinary election such as that between Oliver and George, natural forces will drive these candidates to a situation where their political views each reflect the views of
A) Alice.
B) Mike.
C) Carol.
D) all of the voters.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
46
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. If the figure is viewed as a two-player game between Oliver and George, there would be
A) no Nash equilibria.
B) one Nash equilibrium where both players end up at the M position.
C) two Nash equilibria, one where Oliver ends up at position L4 and George ends up at position C4, and one where both players end up at position M.
D) five Nash equilibria, each represented by the two players ending up an equal distance from M.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. If the figure is viewed as a two-player game between Oliver and George, there would be
A) no Nash equilibria.
B) one Nash equilibrium where both players end up at the M position.
C) two Nash equilibria, one where Oliver ends up at position L4 and George ends up at position C4, and one where both players end up at position M.
D) five Nash equilibria, each represented by the two players ending up an equal distance from M.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
47
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Sam will definitely win the election if he adopts political views that place him at the ________ position(s).
A) M
B) M, L1, or C1
C) L4 or C4
D) Sam cannot possibly win the election.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Sam will definitely win the election if he adopts political views that place him at the ________ position(s).
A) M
B) M, L1, or C1
C) L4 or C4
D) Sam cannot possibly win the election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
48
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate and he espouses political views that place him at the M position. For Oliver to now win the election, he will have to
A) stay at the L4 position.
B) move to the M position.
C) move to the L1 position.
D) move to the C4 position.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate and he espouses political views that place him at the M position. For Oliver to now win the election, he will have to
A) stay at the L4 position.
B) move to the M position.
C) move to the L1 position.
D) move to the C4 position.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
49
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate and he espouses political views that place him at the M position. For George to now win the election, he will have to
A) stay at the C4 position.
B) move to the M position.
C) move to the C1 position.
D) move to the L4 position.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate and he espouses political views that place him at the M position. For George to now win the election, he will have to
A) stay at the C4 position.
B) move to the M position.
C) move to the C1 position.
D) move to the L4 position.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
50
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Oliver refuses to change his political views and so remains at the L4 position. Sam espouses political views that place him at the C2 position. Not wanting to lose any conservative votes to Sam, George decides to alter his political views so he, too, ends up at the C2 position. In this situation, who is indifferent about all three of the candidates?
A) Alice
B) Jan
C) Cindy
D) Peter
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Oliver refuses to change his political views and so remains at the L4 position. Sam espouses political views that place him at the C2 position. Not wanting to lose any conservative votes to Sam, George decides to alter his political views so he, too, ends up at the C2 position. In this situation, who is indifferent about all three of the candidates?
A) Alice
B) Jan
C) Cindy
D) Peter

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
51
Figure 13.2 :  The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Oliver refuses to change his political views and so remains at the L4 position. Sam espouses political views that place him at the C2 position. Not wanting to lose any conservative votes to Sam, George decides to alter his political views so he, too, ends up at the C2 position. In this situation,
A) Sam will definitely win the election.
B) Oliver will definitely win the election.
C) George will definitely win the election.
D) the median voter theorem does not work.
 The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.
The above figure represents the 9 voters in a small community who are voting to elect someone as mayor. The voters are listed in order, from left to right, by their political views, from the most liberal (L4) to the most conservative (C4). The two candidates running for mayor are Oliver Cousins, a liberal, and George Glass, a conservative. Assume that all 9 voters will vote in the election, and each voter will cast his or her vote for the candidate who is most closely aligned with their political views.-Refer to Figure 13.2. Oliver's political views place him at the L4 position and George's political views place him at the C4 position. Based on the two candidates' political views, Sam Butcher decides to enter the race as a third-party candidate. Oliver refuses to change his political views and so remains at the L4 position. Sam espouses political views that place him at the C2 position. Not wanting to lose any conservative votes to Sam, George decides to alter his political views so he, too, ends up at the C2 position. In this situation,
A) Sam will definitely win the election.
B) Oliver will definitely win the election.
C) George will definitely win the election.
D) the median voter theorem does not work.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
52
If the median voter theorem is viewed as a two-player game, with the two players being the candidates running for office, a Nash equilibrium occurs when the candidates hold the most extreme, opposite political views.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
53
In an ordinary election between two candidates, once both candidates have positioned themselves in the political middle, neither has an incentive to move back toward one of the extremes.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
54
The median voter theorem is more likely to hold true in elections with a large number of candidates.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
55
When candidates are chosen in a primary election, they may have to position themselves to win the primary election, leaving them left or right of center in the general election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
56
What are the four types of bias that economist Bryan Caplan believes voters bring with them when they vote? Briefly explain each of these biases.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
57
In many political elections, states often hold a primary election, and the winners of the primary election face off in the general election. This method of voting is called a ________ election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
58
A situation in which the outcome of an election is sensitive to the order of events is called
A) the agenda paradox.
B) strategic voting.
C) the Condorcet paradox.
D) Borda-count manipulation.
A) the agenda paradox.
B) strategic voting.
C) the Condorcet paradox.
D) Borda-count manipulation.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
59
Scenario 13.1: Sammy, Dean, and Frank are having dinner and are trying to decide which appetizer to share. The choices they have are calamari, jalapeno poppers, and potato skins. After doing a quick survey of their preferences, they discover the following:
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Sammy gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; calamari
B) calamari and potato skins; calamari
C) potato skins and jalapeno poppers; potato skins
D) jalapeno poppers and potato skins; jalapeno poppers
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Sammy gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; calamari
B) calamari and potato skins; calamari
C) potato skins and jalapeno poppers; potato skins
D) jalapeno poppers and potato skins; jalapeno poppers

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
60
Scenario 13.1: Sammy, Dean, and Frank are having dinner and are trying to decide which appetizer to share. The choices they have are calamari, jalapeno poppers, and potato skins. After doing a quick survey of their preferences, they discover the following:
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Dean gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; jalapeno poppers
B) calamari and potato skins; potato skins
C) potato skins and calamari; calamari
D) jalapeno poppers and potato skins; jalapeno poppers
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Dean gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; jalapeno poppers
B) calamari and potato skins; potato skins
C) potato skins and calamari; calamari
D) jalapeno poppers and potato skins; jalapeno poppers

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
61
Scenario 13.1: Sammy, Dean, and Frank are having dinner and are trying to decide which appetizer to share. The choices they have are calamari, jalapeno poppers, and potato skins. After doing a quick survey of their preferences, they discover the following:
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Frank gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; jalapeno poppers
B) jalapeno poppers and calamari; calamari
C) potato skins and calamari; potato skins
D) jalapeno poppers and potato skins; potato skins
- Sammy prefers calamari to jalapeno poppers and jalapeno poppers to potato skins.
- Dean prefers jalapeno poppers to potato skins and potato skins to calamari.
- Frank prefers potato skins to calamari and calamari to jalapeno poppers.
They decide to have a runoff election since there is no clear winner by pitting two choices against each other in a preliminary round, and the winner will face off against the remaining choice in the final round.
-Refer to Scenario 13.1. If Frank gets to set the agenda, he will pit ________ in the first round to assure that ________ wins the first round vote.
A) calamari and jalapeno poppers; jalapeno poppers
B) jalapeno poppers and calamari; calamari
C) potato skins and calamari; potato skins
D) jalapeno poppers and potato skins; potato skins

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
62
Voting in accordance with one's true preference is called
A) ballot manipulation.
B) strategic voting.
C) naive voting.
D) the voting paradox.
A) ballot manipulation.
B) strategic voting.
C) naive voting.
D) the voting paradox.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
63
Voting against ones preferences in the initial round of a runoff election in order to prevent the selection of an undesirable alternative in the final round is called
A) ballot manipulation.
B) strategic voting.
C) naive voting.
D) the voting paradox.
A) ballot manipulation.
B) strategic voting.
C) naive voting.
D) the voting paradox.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
64
If Terry sets the agenda for an election, she can possibly manipulate the outcome based on the order of events to be voted on.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
65
Andrew is unfamiliar with any of the candidates positions, so he rolls a dice to decide who to vote for in the governor's election. This is an example of naive voting.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
66
Strategic voting can reduce the power of someone trying to manipulate the outcome of an election.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
67
Ann Marie is a Tea-Party Republican, but she decides to vote in the Democratic primary in order to vote against the most liberal candidate. This is an example of strategic voting.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
68
Briefly explain the difference between naive voting and strategic voting.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
69
Explain how not knowing whether someone will vote naively or strategically could make vote manipulation through agenda setting more difficult.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck


