Deck 9: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 9: Differential Equations
1
Find the general solution of the differential equation. Use C, C1, C2, . . . to denote arbitrary constants. If used, do not simplify hyperbolic functions.
-y'(t) = 3 +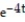
A) y = 3t -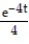 + C
+ C
B) y = 3t +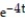 + C
+ C
C) y = -4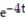 + C
+ C
D) y = 3 -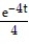 + C
+ C
-y'(t) = 3 +
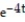
A) y = 3t -
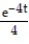 + C
+ CB) y = 3t +
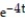 + C
+ CC) y = -4
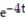 + C
+ CD) y = 3 -
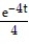 + C
+ Cy = 3t - 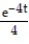 + C
+ C
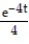 + C
+ C 2
Find the general solution of the differential equation. Use C, C1, C2, . . . to denote arbitrary constants. If used, do not simplify hyperbolic functions.
-y'(t) = 14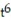 - 16
- 16 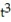 + 8 - 12
+ 8 - 12 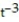
A)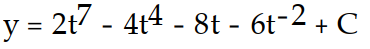
B)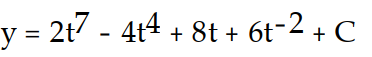
C)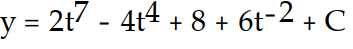
D)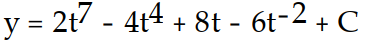
-y'(t) = 14
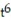 - 16
- 16 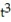 + 8 - 12
+ 8 - 12 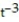
A)
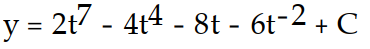
B)
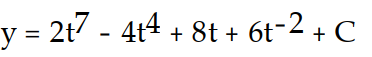
C)
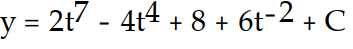
D)
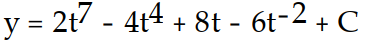
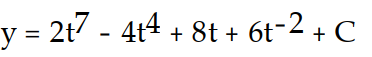
3
Find the general solution of the differential equation. Use C, C1, C2, . . . to denote arbitrary constants. If used, do not simplify hyperbolic functions.
-p'(x) =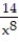 - 5 + 12
- 5 + 12 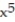
A)
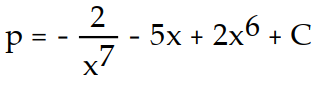
B)
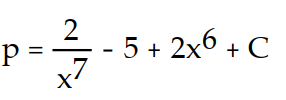
C)
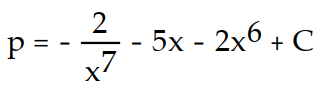
D)
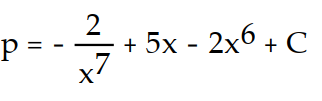
-p'(x) =
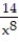 - 5 + 12
- 5 + 12 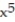
A)
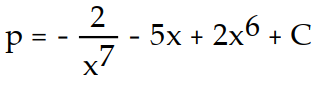
B)
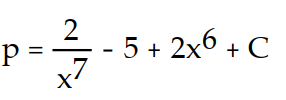
C)
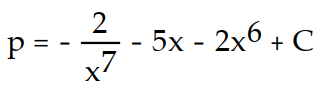
D)
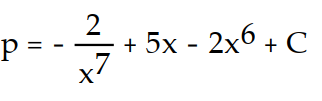
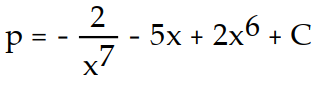
4
Find the general solution of the differential equation. Use C, C1, C2, . . . to denote arbitrary constants. If used, do not simplify hyperbolic functions.
-y''(t) = 45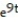 + sin 5t
+ sin 5t
A)
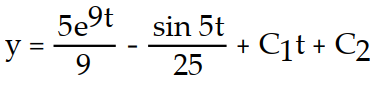
B)
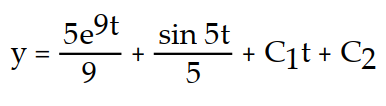
C)
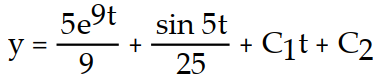
D)
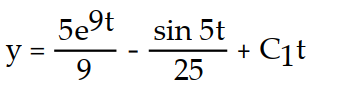
-y''(t) = 45
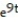 + sin 5t
+ sin 5tA)
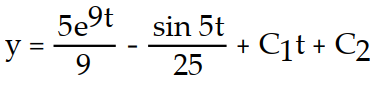
B)
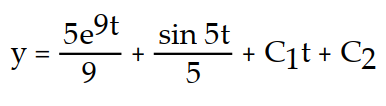
C)
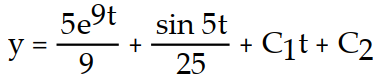
D)
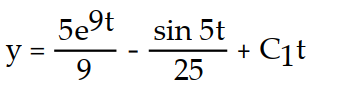

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
Find the general solution of the differential equation. Use C, C1, C2, . . . to denote arbitrary constants. If used, do not simplify hyperbolic functions.
-v'(t) =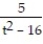
A)
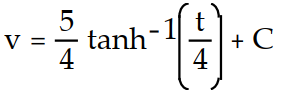
B)
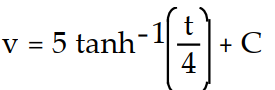
C)
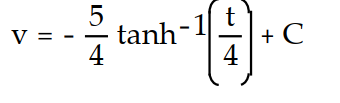
D)
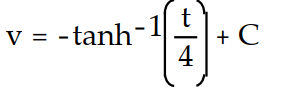
-v'(t) =
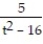
A)
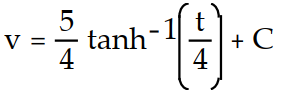
B)
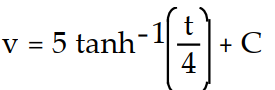
C)
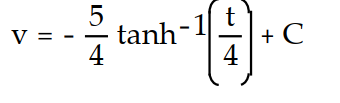
D)
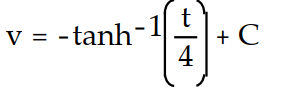

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the initial value problem.
-y'(x) = 18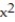 - 9
- 9 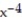 , y(1) = 0
, y(1) = 0
A) y = 6x3 + 3x-3
B) y = 6x3 + 3x -3- 9
C) y = 6x3 + 3x -3+ 9
D) y = 6x3 - 3x -3+ 9
-y'(x) = 18
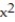 - 9
- 9 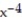 , y(1) = 0
, y(1) = 0A) y = 6x3 + 3x-3
B) y = 6x3 + 3x -3- 9
C) y = 6x3 + 3x -3+ 9
D) y = 6x3 - 3x -3+ 9

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the initial value problem.
-y'(x) = 4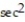 2x, y(0) = 5
2x, y(0) = 5
A) y = 2 tan 2x - 5
B) y = 2 tan 2x + 4
C) y = 2 tan 2x + 5
D) y = 4 tan 2x + 5
-y'(x) = 4
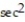 2x, y(0) = 5
2x, y(0) = 5A) y = 2 tan 2x - 5
B) y = 2 tan 2x + 4
C) y = 2 tan 2x + 5
D) y = 4 tan 2x + 5

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the initial value problem.
-u''(x) = 12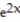 - 12
- 12 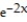 , u(0) = 12, u'(0) = 16
, u(0) = 12, u'(0) = 16
A)
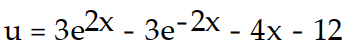
B)
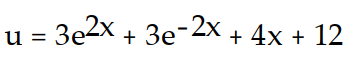
C)
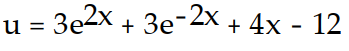
D)
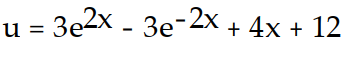
-u''(x) = 12
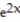 - 12
- 12 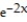 , u(0) = 12, u'(0) = 16
, u(0) = 12, u'(0) = 16A)
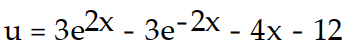
B)
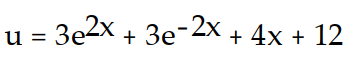
C)
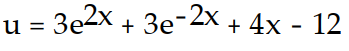
D)
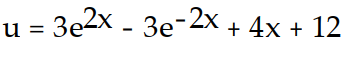

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the initial value problem.
-u'(x) =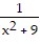 - 6, u(0) = 5
- 6, u(0) = 5
A)
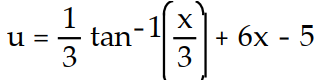
B)
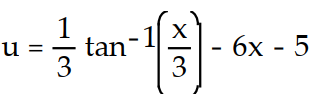
C)
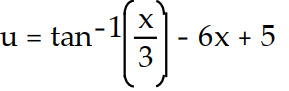
D)
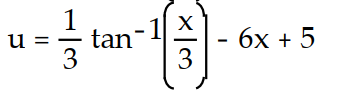
-u'(x) =
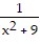 - 6, u(0) = 5
- 6, u(0) = 5A)
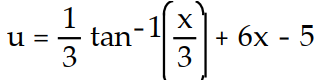
B)
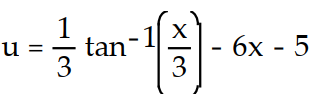
C)
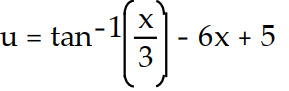
D)
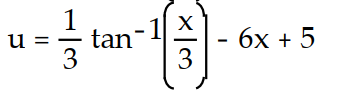

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the problem.
-An object is fired vertically upward with an initial velocity v(0) = v0 from an initial position s(0) = s0 . Assuming no air resistance, the position of the object is governed by the differential equation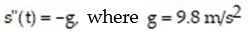 is the acceleration due to gravity (in the downward direction). For the following values of v0 and s0 , find the position and velocity functions for all times at which the object is above the ground. Then find the time at which the highest point of the trajectory is reached and the height of the object at that time.
is the acceleration due to gravity (in the downward direction). For the following values of v0 and s0 , find the position and velocity functions for all times at which the object is above the ground. Then find the time at which the highest point of the trajectory is reached and the height of the object at that time.
v0 = 39.2 m/s , s0 = 40 m
A) s = -9.8 + 39.2t + 40, v = -9.8t; Highest point of 118.4 m is reached at t = 5 s
B) s = -9.8 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 4 s
C) s = -4.9 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 5 s
D) s = -4.9 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 4 s
-An object is fired vertically upward with an initial velocity v(0) = v0 from an initial position s(0) = s0 . Assuming no air resistance, the position of the object is governed by the differential equation
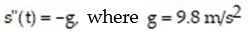 is the acceleration due to gravity (in the downward direction). For the following values of v0 and s0 , find the position and velocity functions for all times at which the object is above the ground. Then find the time at which the highest point of the trajectory is reached and the height of the object at that time.
is the acceleration due to gravity (in the downward direction). For the following values of v0 and s0 , find the position and velocity functions for all times at which the object is above the ground. Then find the time at which the highest point of the trajectory is reached and the height of the object at that time.v0 = 39.2 m/s , s0 = 40 m
A) s = -9.8 + 39.2t + 40, v = -9.8t; Highest point of 118.4 m is reached at t = 5 s
B) s = -9.8 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 4 s
C) s = -4.9 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 5 s
D) s = -4.9 + 39.2t + 40, v = -9.8t + 39.2; Highest point of 118.4 m is reached at t = 4 s

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the problem.
-A simple model of a harvested resource follows the equation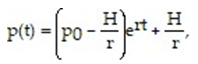 where p(t) is the amount (or population) of the resource at time
where p(t) is the amount (or population) of the resource at time 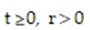 is the natural growth rate of the resource, and H > 0 is the harvesting rate. If
is the natural growth rate of the resource, and H > 0 is the harvesting rate. If 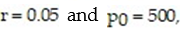 for what values of H is the amount of the resource increasing? For what value of H is the amount of the resource constant?
for what values of H is the amount of the resource increasing? For what value of H is the amount of the resource constant?
A) H < 25; H = 25
B) H < 25; H > 25
C) H > 25; H = 25
D) H < 50; H < 50
-A simple model of a harvested resource follows the equation
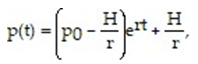 where p(t) is the amount (or population) of the resource at time
where p(t) is the amount (or population) of the resource at time 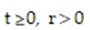 is the natural growth rate of the resource, and H > 0 is the harvesting rate. If
is the natural growth rate of the resource, and H > 0 is the harvesting rate. If 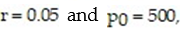 for what values of H is the amount of the resource increasing? For what value of H is the amount of the resource constant?
for what values of H is the amount of the resource increasing? For what value of H is the amount of the resource constant? A) H < 25; H = 25
B) H < 25; H > 25
C) H > 25; H = 25
D) H < 50; H < 50

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the problem.
-Imagine a large tank with cross-sectional area A. The bottom of the tank has a circular drain with cross-sectional area a. Assume the tank is initially filled with water to a height h(0) = H. The height of the water as it flows out of the tank is described by the equation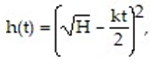 where
where 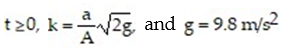 is the acceleration due to gravity. Find the water height function for
is the acceleration due to gravity. Find the water height function for 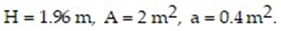 Then determine the approximate time at which the tank is first empty. If necessary, round to two decimal places.
Then determine the approximate time at which the tank is first empty. If necessary, round to two decimal places.
A)
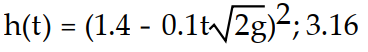
B)
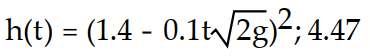
C)
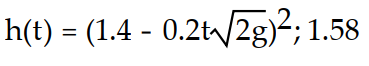
D)
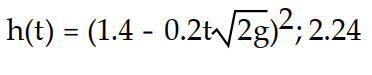
-Imagine a large tank with cross-sectional area A. The bottom of the tank has a circular drain with cross-sectional area a. Assume the tank is initially filled with water to a height h(0) = H. The height of the water as it flows out of the tank is described by the equation
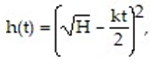 where
where 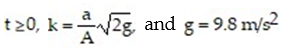 is the acceleration due to gravity. Find the water height function for
is the acceleration due to gravity. Find the water height function for 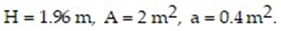 Then determine the approximate time at which the tank is first empty. If necessary, round to two decimal places.
Then determine the approximate time at which the tank is first empty. If necessary, round to two decimal places. A)
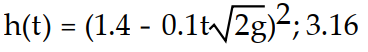
B)
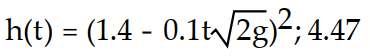
C)
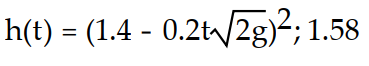
D)
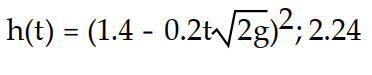

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
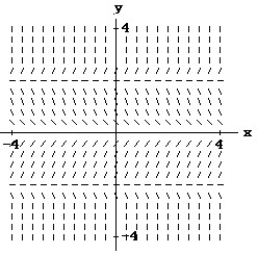
Match the differential equation with the appropriate direction field.
-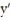 (x) = y + 2
(x) = y + 2
A)
B)
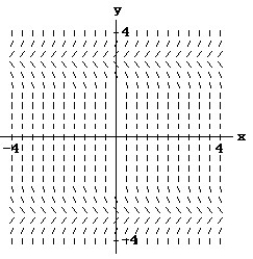
C)
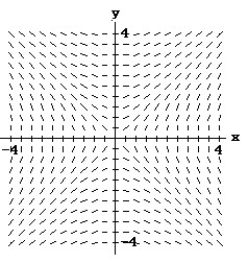
D)
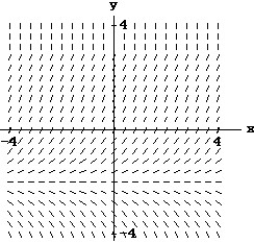
-
 (x) = y + 2
(x) = y + 2A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
Match the differential equation with the appropriate direction field.
-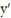 (x) =
(x) = 
A)
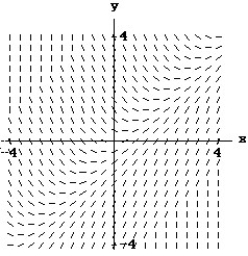
B)
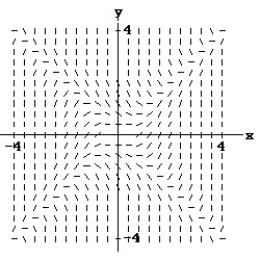
C)
D)
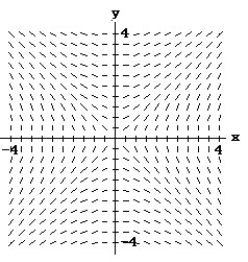
-
 (x) =
(x) = 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
Match the differential equation with the appropriate direction field.
-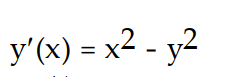
A)
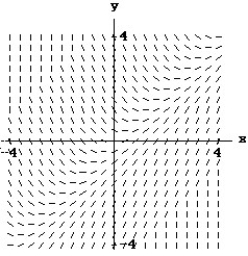
B)
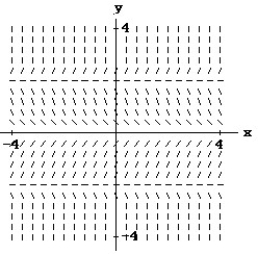
C)
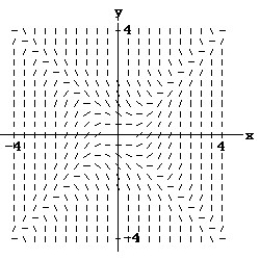
D)
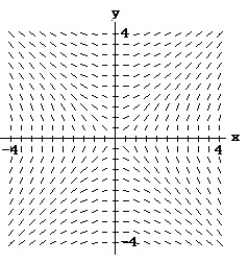
-
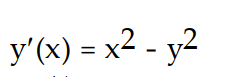
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
Use the given window to sketch a direction field for the equation. Then sketch the solution curve that corresponds to the given initial condition. A detailed direction field is not needed.
-y'(x) = y(3 - y), y(0) =![Use the given window to sketch a direction field for the equation. Then sketch the solution curve that corresponds to the given initial condition. A detailed direction field is not needed. -y'(x) = y(3 - y), y(0) = ; [0, 5] × [0, 4]](https://storage.examlex.com/TB9662/11ee9522_3431_f5ef_bdb6_2176ec7f5c8d_TB9662_11.jpg) ; [0, 5] × [0, 4]
; [0, 5] × [0, 4]
![Use the given window to sketch a direction field for the equation. Then sketch the solution curve that corresponds to the given initial condition. A detailed direction field is not needed. -y'(x) = y(3 - y), y(0) = ; [0, 5] × [0, 4]](https://storage.examlex.com/TB9662/11ee9522_3431_f5f0_bdb6_0dfdf585131a_TB9662_11.jpg)
-y'(x) = y(3 - y), y(0) =
![Use the given window to sketch a direction field for the equation. Then sketch the solution curve that corresponds to the given initial condition. A detailed direction field is not needed. -y'(x) = y(3 - y), y(0) = ; [0, 5] × [0, 4]](https://storage.examlex.com/TB9662/11ee9522_3431_f5ef_bdb6_2176ec7f5c8d_TB9662_11.jpg) ; [0, 5] × [0, 4]
; [0, 5] × [0, 4] ![Use the given window to sketch a direction field for the equation. Then sketch the solution curve that corresponds to the given initial condition. A detailed direction field is not needed. -y'(x) = y(3 - y), y(0) = ; [0, 5] × [0, 4]](https://storage.examlex.com/TB9662/11ee9522_3431_f5f0_bdb6_0dfdf585131a_TB9662_11.jpg)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the differential equation. A detailed direction field is not needed. Find the solutions that are constant, for all 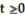 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?
-y'(t) = (y - 4)( 4 + y)
A)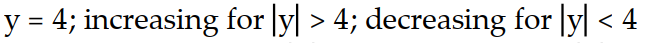
B)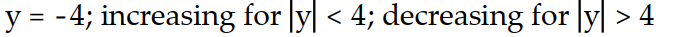
C)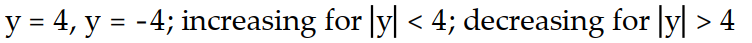
D)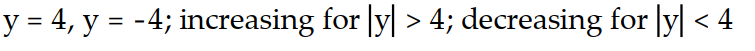
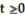 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?-y'(t) = (y - 4)( 4 + y)
A)
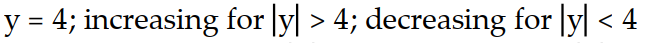
B)
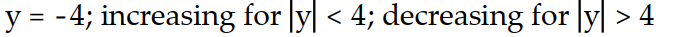
C)
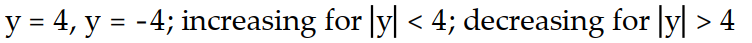
D)
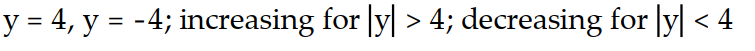

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the differential equation. A detailed direction field is not needed. Find the solutions that are constant, for all 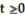 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?
-y'(t) = (y - 2)(y + 7)
A) y = -2, y = 7; increasing for y < -7 or y > 2; decreasing for -7 < y < 2
B) y = 2, y = -7; increasing for y < -7 or y > 2; decreasing for -7 < y < 2
C)y = -2, y = 7; increasing for -7 < y < 2; decreasing for y < -7 or y > 2
D) y = 2, y = -7; increasing for -7 < y < 2; decreasing for y < -7 or y > 2
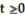 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?-y'(t) = (y - 2)(y + 7)
A) y = -2, y = 7; increasing for y < -7 or y > 2; decreasing for -7 < y < 2
B) y = 2, y = -7; increasing for y < -7 or y > 2; decreasing for -7 < y < 2
C)y = -2, y = 7; increasing for -7 < y < 2; decreasing for y < -7 or y > 2
D) y = 2, y = -7; increasing for -7 < y < 2; decreasing for y < -7 or y > 2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the differential equation. A detailed direction field is not needed. Find the solutions that are constant, for all 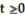 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?
-y'(t) = y(y + 4)( 6 - y)
A) y = -4, y = 6; increasing for -4 < y < 6; decreasing for y < -4, y > 6
B) y = 0, y = -4, y = 6; increasing for y < -4, 0 < y < 6; decreasing for -4 < y < 0, y > 6
C) y = 0, y = -4, y = 6; increasing for -4 < y < 0; decreasing for y < -4, y > 0
D) y = -4, y = 6; increasing for y < -4, 0 < y < 6; decreasing for -4 < y < 0, y > 6
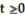 (the equilibrium solutions). In what regions are solutions increasing? Decreasing?
(the equilibrium solutions). In what regions are solutions increasing? Decreasing?-y'(t) = y(y + 4)( 6 - y)
A) y = -4, y = 6; increasing for -4 < y < 6; decreasing for y < -4, y > 6
B) y = 0, y = -4, y = 6; increasing for y < -4, 0 < y < 6; decreasing for -4 < y < 0, y > 6
C) y = 0, y = -4, y = 6; increasing for -4 < y < 0; decreasing for y < -4, y > 0
D) y = -4, y = 6; increasing for y < -4, 0 < y < 6; decreasing for -4 < y < 0, y > 6

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the logistic equation. Find the equilibrium solutions. A detailed direction field is not needed. Assume 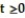 and
and 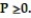
-P'(t) = 0.1P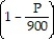
A) P = 0 and P = 450
B) P = 450
C) P = 0 and P = 225
D) P = 0 and P = 900
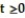 and
and 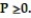
-P'(t) = 0.1P
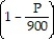
A) P = 0 and P = 450
B) P = 450
C) P = 0 and P = 225
D) P = 0 and P = 900

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the logistic equation. Find the equilibrium solutions. A detailed direction field is not needed. Assume 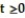 and
and 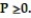
-P'(t) = 0.05P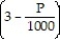
A) P = 0 and P = 1500
B) P = 0 and P = 3000
C) P = 0 and P = 750
D) P = 1500
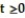 and
and 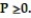
-P'(t) = 0.05P
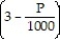
A) P = 0 and P = 1500
B) P = 0 and P = 3000
C) P = 0 and P = 750
D) P = 1500

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the logistic equation. Find the equilibrium solutions. A detailed direction field is not needed. Assume 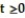 and
and 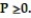
-P'(t) = 0.1P - 0.002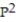
A) P = 0 and P = 60
B) P = 50
C) P = 0 and P = 50
D) P = 0 and P = 100
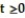 and
and 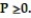
-P'(t) = 0.1P - 0.002
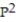
A) P = 0 and P = 60
B) P = 50
C) P = 0 and P = 50
D) P = 0 and P = 100

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
For the initial value problem, compute the first two approximations 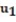 and
and 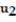 given by Euler's method using the given time step.
given by Euler's method using the given time step.
-y'(t) = 6y, y(0) = 4; t = 0.5
A)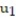 = 16;
= 16; 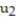 = 112
= 112
B)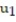 = 16;
= 16; 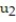 = 64
= 64
C)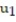 = 28;
= 28; 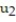 = 112
= 112
D)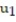 = 4;
= 4; 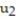 = 16
= 16
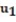 and
and 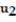 given by Euler's method using the given time step.
given by Euler's method using the given time step.-y'(t) = 6y, y(0) = 4; t = 0.5
A)
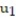 = 16;
= 16; 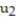 = 112
= 112B)
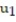 = 16;
= 16; 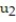 = 64
= 64C)
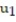 = 28;
= 28; 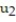 = 112
= 112D)
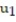 = 4;
= 4; 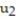 = 16
= 16
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
For the initial value problem, compute the first two approximations 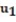 and
and 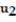 given by Euler's method using the given time step.
given by Euler's method using the given time step.
-y'(t) = 4 - y, y(0) = 4; t = 0.1
A)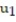 = 4;
= 4; 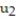 = 4
= 4
B)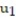 = 4.8;
= 4.8; 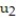 = 4
= 4
C)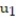 = 4.8;
= 4.8; 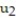 = 4.72
= 4.72
D)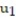 = 4;
= 4; 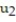 = 4.72
= 4.72
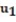 and
and 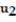 given by Euler's method using the given time step.
given by Euler's method using the given time step.-y'(t) = 4 - y, y(0) = 4; t = 0.1
A)
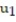 = 4;
= 4; 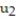 = 4
= 4B)
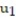 = 4.8;
= 4.8; 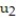 = 4
= 4C)
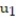 = 4.8;
= 4.8; 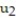 = 4.72
= 4.72D)
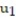 = 4;
= 4; 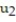 = 4.72
= 4.72
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
For the initial value problem, compute the first two approximations 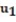 and
and 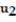 given by Euler's method using the given time step.
given by Euler's method using the given time step.
-y'(t) = -y, y(0) = -3; t = 0.1
A)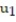 = -2;
= -2; 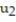 = - 2.61
= - 2.61
B)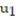 = -2.7;
= -2.7; 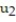 = -2.7
= -2.7
C)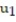 = -2.7;
= -2.7; 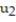 = -2.43
= -2.43
D)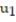 = -3;
= -3; 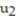 = -2.7
= -2.7
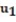 and
and 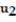 given by Euler's method using the given time step.
given by Euler's method using the given time step.-y'(t) = -y, y(0) = -3; t = 0.1
A)
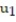 = -2;
= -2; 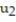 = - 2.61
= - 2.61B)
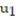 = -2.7;
= -2.7; 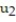 = -2.7
= -2.7C)
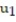 = -2.7;
= -2.7; 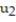 = -2.43
= -2.43D)
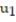 = -3;
= -3; 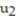 = -2.7
= -2.7
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the initial value problem. Find the approximations of y(0.2) and y(0.4) using Euler's method with a time step of 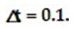 Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
-y'(t) = 5 - y, y(0) = 4; y(t) = 5 -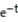
A)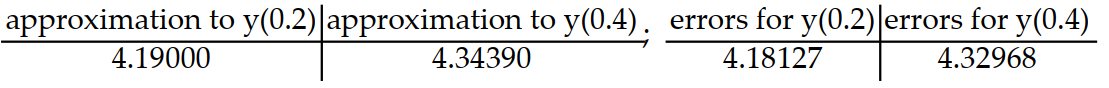
B)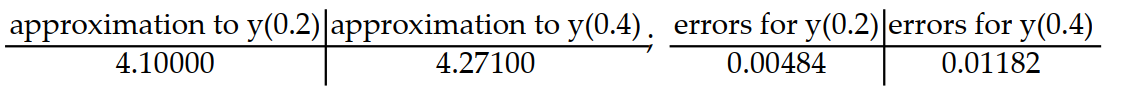
C)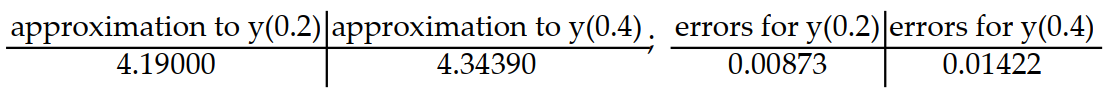
D)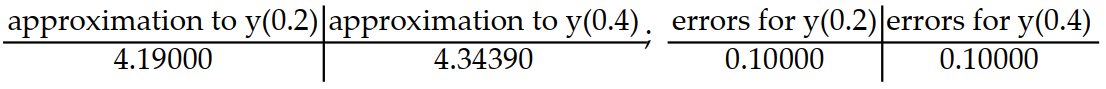
 Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding. -y'(t) = 5 - y, y(0) = 4; y(t) = 5 -
A)
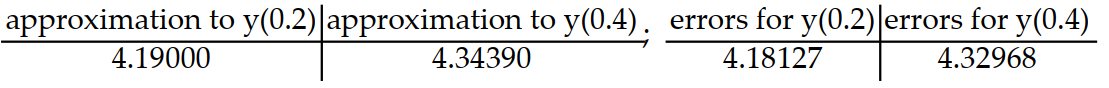
B)
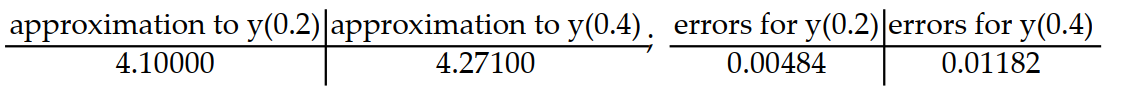
C)
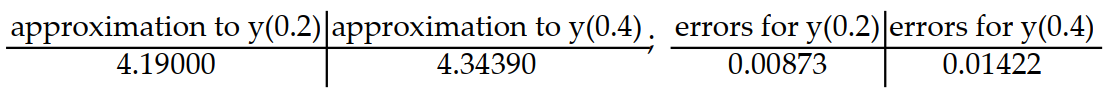
D)
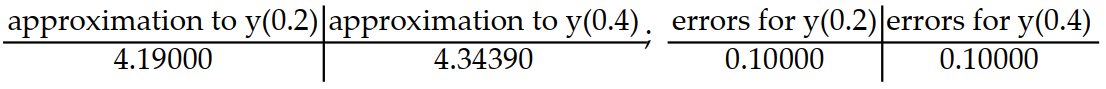

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the initial value problem. Find the approximations of y(0.2) and y(0.4) using Euler's method with a time step of 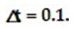 Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
-y'(t) =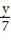 , y(0) = 7; y(t) = 7
, y(0) = 7; y(t) = 7 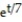
A)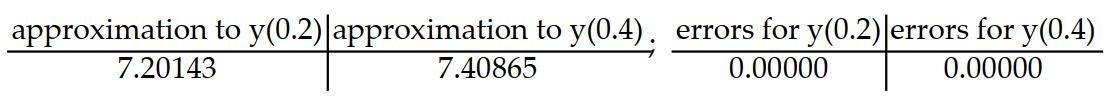
B)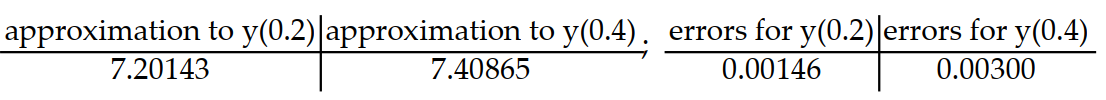
C)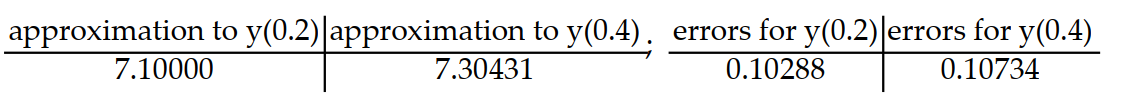
D)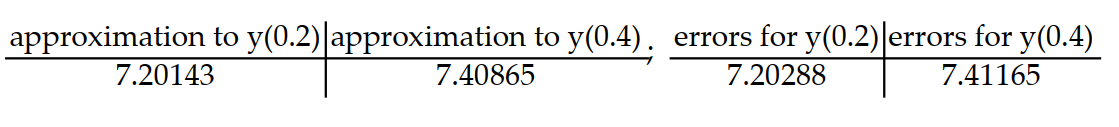
 Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding.
Then using the exact solution given, compute the errors in the Euler approximations at t = 0.2 and t = 0.4 Round answers to five decimal places, do not use intermediate rounding. -y'(t) =
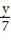 , y(0) = 7; y(t) = 7
, y(0) = 7; y(t) = 7 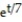
A)
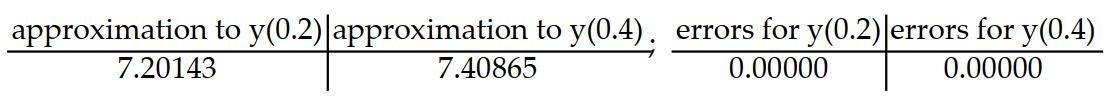
B)
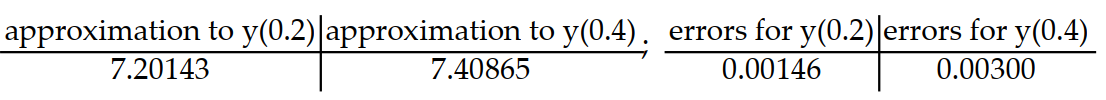
C)
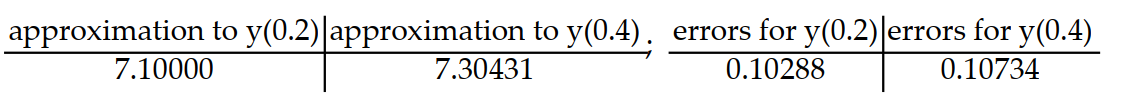
D)
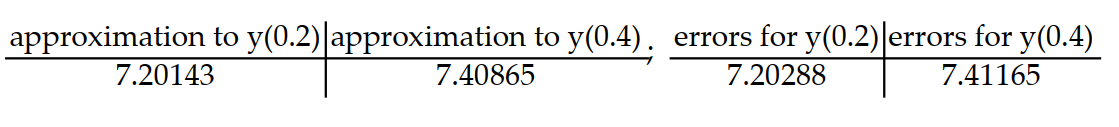

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding.
-y'(t) = -4y, y(0) = 1; t = 0.2, T = 1; y(t) =![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = -4y, y(0) = 1; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 0.00032; 0.01800 B) y(1) \approx 0.00032; 0.20000 C)y(1) \approx 0.00160; 0.01672 D) y(1) \approx 0.00032; 0.01832](https://storage.examlex.com/TB9662/11ee9522_3433_55b2_bdb6_37a56b62a87c_TB9662_11.jpg)
A) y(1) 0.00032; 0.01800
B) y(1) 0.00032; 0.20000
C)y(1) 0.00160; 0.01672
D) y(1) 0.00032; 0.01832
-y'(t) = -4y, y(0) = 1; t = 0.2, T = 1; y(t) =
![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = -4y, y(0) = 1; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 0.00032; 0.01800 B) y(1) \approx 0.00032; 0.20000 C)y(1) \approx 0.00160; 0.01672 D) y(1) \approx 0.00032; 0.01832](https://storage.examlex.com/TB9662/11ee9522_3433_55b2_bdb6_37a56b62a87c_TB9662_11.jpg)
A) y(1) 0.00032; 0.01800
B) y(1) 0.00032; 0.20000
C)y(1) 0.00160; 0.01672
D) y(1) 0.00032; 0.01832

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding.
-y'(t) =![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = , y(0) = 4; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 4.12311; 0.024824 B) y(1) \approx 4.14793; 0.024824 C) y(1) \approx 4.14793; 4.12311 D) y(1) \approx 4.14793; 0.20000](https://storage.examlex.com/TB9662/11ee9522_3433_7bc3_bdb6_4769890a0ac8_TB9662_11.jpg) , y(0) = 4; t = 0.2, T = 1; y(t) =
, y(0) = 4; t = 0.2, T = 1; y(t) = ![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = , y(0) = 4; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 4.12311; 0.024824 B) y(1) \approx 4.14793; 0.024824 C) y(1) \approx 4.14793; 4.12311 D) y(1) \approx 4.14793; 0.20000](https://storage.examlex.com/TB9662/11ee9522_3433_7bc4_bdb6_03abf0a8b108_TB9662_11.jpg)
A) y(1) 4.12311; 0.024824
B) y(1) 4.14793; 0.024824
C) y(1) 4.14793; 4.12311
D) y(1) 4.14793; 0.20000
-y'(t) =
![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = , y(0) = 4; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 4.12311; 0.024824 B) y(1) \approx 4.14793; 0.024824 C) y(1) \approx 4.14793; 4.12311 D) y(1) \approx 4.14793; 0.20000](https://storage.examlex.com/TB9662/11ee9522_3433_7bc3_bdb6_4769890a0ac8_TB9662_11.jpg) , y(0) = 4; t = 0.2, T = 1; y(t) =
, y(0) = 4; t = 0.2, T = 1; y(t) = ![<strong>Use a calculator or computer program to approximate the value of y(T) using Euler's method with the given time step on the interval [0, T]. Then, using the exact solution given, find the error in the approximation to y(T) (only at the right endpoint of the time interval). Round answers to five decimal places, do not use intermediate rounding. -y'(t) = , y(0) = 4; \Delta t = 0.2, T = 1; y(t) = </strong> A) y(1) \approx 4.12311; 0.024824 B) y(1) \approx 4.14793; 0.024824 C) y(1) \approx 4.14793; 4.12311 D) y(1) \approx 4.14793; 0.20000](https://storage.examlex.com/TB9662/11ee9522_3433_7bc4_bdb6_03abf0a8b108_TB9662_11.jpg)
A) y(1) 4.12311; 0.024824
B) y(1) 4.14793; 0.024824
C) y(1) 4.14793; 4.12311
D) y(1) 4.14793; 0.20000

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
-The delivery of a drug (such as an antibiotic) through an intravenous line may be modeled by the differential equation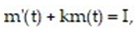 where m(t) is the mass of the drug in the blood at time
where m(t) is the mass of the drug in the blood at time 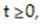 k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let
k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let 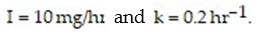 For what initial values m(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
For what initial values m(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
A) increasing for A < 50 and decreasing for A > 50; m(t) = 0
B) increasing for A > 50 and decreasing for A < 50; m(t) = 0
C) increasing for A < 50 and decreasing for A > 50; m(t) = 50
D) increasing for A > 50 and decreasing for A < 50; m(t) = 50
-The delivery of a drug (such as an antibiotic) through an intravenous line may be modeled by the differential equation
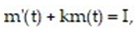 where m(t) is the mass of the drug in the blood at time
where m(t) is the mass of the drug in the blood at time 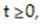 k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let
k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let 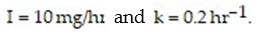 For what initial values m(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
For what initial values m(0) = A are solutions increasing? decreasing? What is the equilibrium solution? A) increasing for A < 50 and decreasing for A > 50; m(t) = 0
B) increasing for A > 50 and decreasing for A < 50; m(t) = 0
C) increasing for A < 50 and decreasing for A > 50; m(t) = 50
D) increasing for A > 50 and decreasing for A < 50; m(t) = 50

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
-A model that describes the free fall of an object in a gravitational field subject to air resistance uses the equation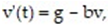 where v(t) is the velocity of the object, for
where v(t) is the velocity of the object, for 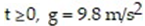 is the acceleration due to gravity, and b > 0 is a constant that involve the mass of the object and the air resistance. Let b = 0.2s-1 For what initial values v(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
is the acceleration due to gravity, and b > 0 is a constant that involve the mass of the object and the air resistance. Let b = 0.2s-1 For what initial values v(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
A) increasing for A < 49 and decreasing for A > 49; v(t) = 49
B) increasing for A < 49 and decreasing for A > 49; v(t) = 0
C) increasing for A > 49 and decreasing for A < 49; v(t) = 49
D) increasing for A > 49 and decreasing for A < 49; v(t) = 0
-A model that describes the free fall of an object in a gravitational field subject to air resistance uses the equation
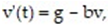 where v(t) is the velocity of the object, for
where v(t) is the velocity of the object, for 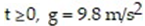 is the acceleration due to gravity, and b > 0 is a constant that involve the mass of the object and the air resistance. Let b = 0.2s-1 For what initial values v(0) = A are solutions increasing? decreasing? What is the equilibrium solution?
is the acceleration due to gravity, and b > 0 is a constant that involve the mass of the object and the air resistance. Let b = 0.2s-1 For what initial values v(0) = A are solutions increasing? decreasing? What is the equilibrium solution? A) increasing for A < 49 and decreasing for A > 49; v(t) = 49
B) increasing for A < 49 and decreasing for A > 49; v(t) = 0
C) increasing for A > 49 and decreasing for A < 49; v(t) = 49
D) increasing for A > 49 and decreasing for A < 49; v(t) = 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-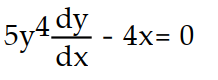
A) y = -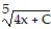
B) y = -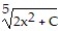
C) y =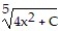
D) y =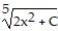
-
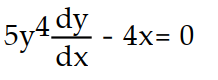
A) y = -
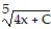
B) y = -
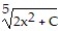
C) y =
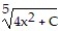
D) y =
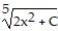

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-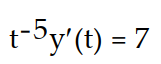
A)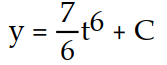
B) y = 42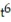 + C
+ C
C) y = 49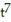 + C
+ C
D)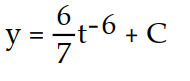
-
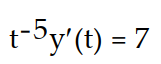
A)
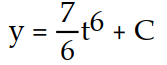
B) y = 42
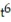 + C
+ CC) y = 49
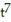 + C
+ CD)
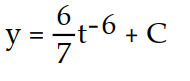

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-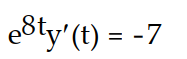
A)
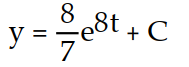
B)
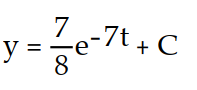
C)
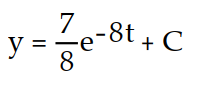
D) y = 56 + C
+ C
-
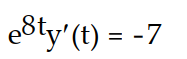
A)
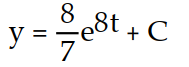
B)
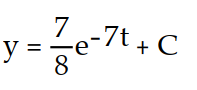
C)
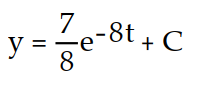
D) y = 56
 + C
+ C
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-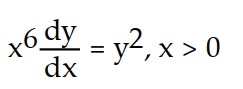
A)
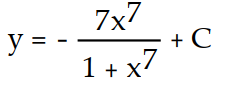
B)
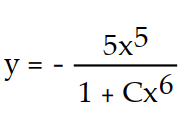
C)
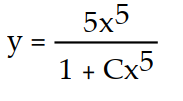
D)
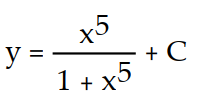
-
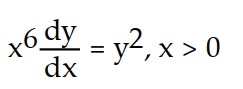
A)
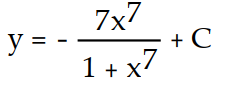
B)
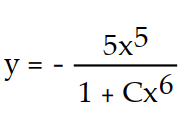
C)
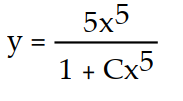
D)
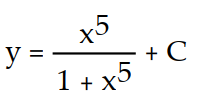

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-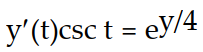
A)
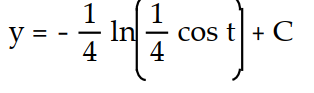
B)
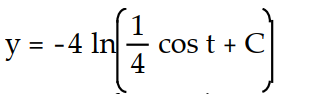
C)
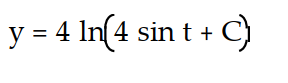
D)
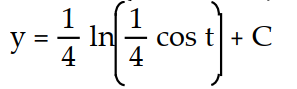
-
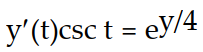
A)
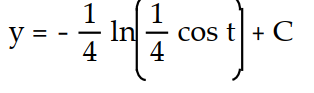
B)
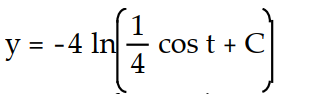
C)
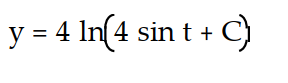
D)
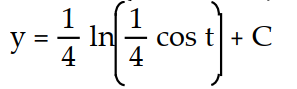

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Find the general solution of the equation. Express the solution explicitly as a function of the independent variable.
-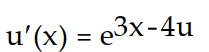
A)
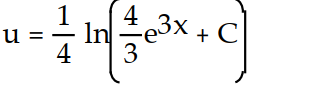
B)
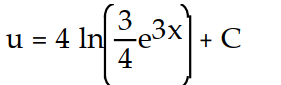
C)
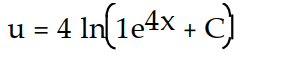
D)
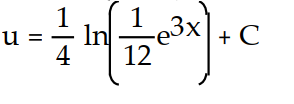
-
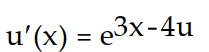
A)
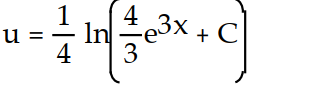
B)
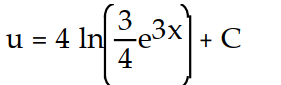
C)
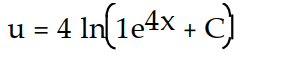
D)
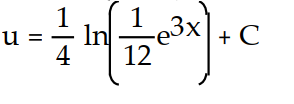

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the initial value problem, if possible.
-csc x (t) = 1, y
(t) = 1, y  = 1
= 1
A) y = -cos t + 1
B) y = -cot t + 1
C) y = -sin t + 1
D) y = cos t +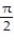
-csc x
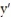 (t) = 1, y
(t) = 1, y 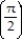 = 1
= 1A) y = -cos t + 1
B) y = -cot t + 1
C) y = -sin t + 1
D) y = cos t +

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the initial value problem, if possible.
-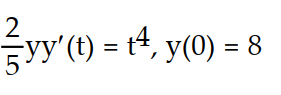
A) y =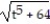
B) y = 5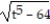
C) y =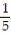
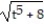
D) y =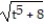
-
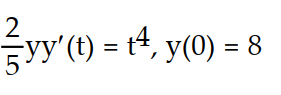
A) y =
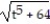
B) y = 5
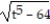
C) y =
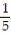
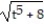
D) y =
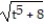

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the initial value problem, if possible.
-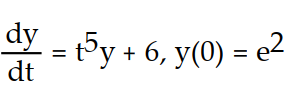
A) y =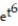 + 2
+ 2
B) y =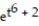
C) y = 6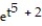
D) Not separable
-
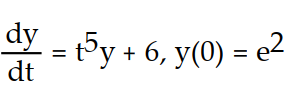
A) y =
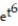 + 2
+ 2B) y =
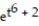
C) y = 6
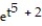
D) Not separable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the initial value problem, if possible.
-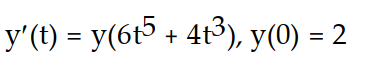
A) y = 2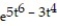
B) y = 2 ln(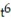 +
+ 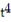 )
)
C)y = 2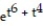
D) y =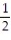
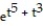
-
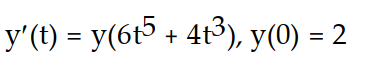
A) y = 2
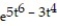
B) y = 2 ln(
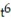 +
+ 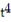 )
)C)y = 2
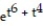
D) y =
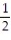
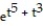

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the initial value problem, if possible.
-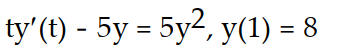
A) y =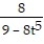
B) y =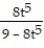
C) Not separable
D) y =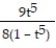
-
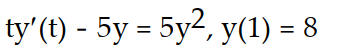
A) y =
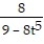
B) y =
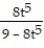
C) Not separable
D) y =
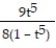

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the initial value problem and leave the solution in implicit form.
-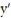 (t) =
(t) = 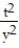 , y( 0) = 2
, y( 0) = 2
A)
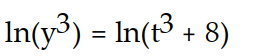
B)
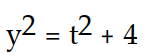
C)
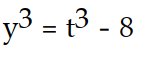
D)
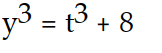
-
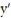 (t) =
(t) = 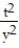 , y( 0) = 2
, y( 0) = 2A)
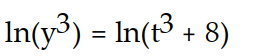
B)
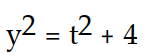
C)
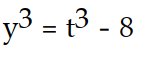
D)
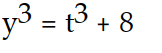

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the initial value problem and leave the solution in implicit form.
-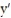 (x) =
(x) = 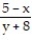 , y( -3) = -3
, y( -3) = -3
A)
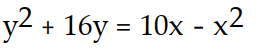
B)
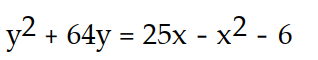
C)
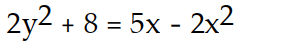
D)
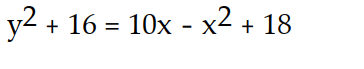
-
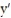 (x) =
(x) = 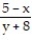 , y( -3) = -3
, y( -3) = -3A)
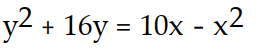
B)
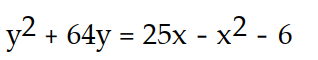
C)
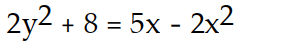
D)
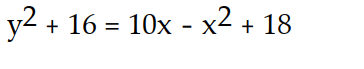

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the initial value problem and leave the solution in implicit form.
-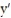 (x)
(x) 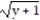 =
= 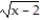 , y( 3) = 24
, y( 3) = 24
A)
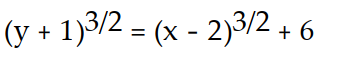
B)
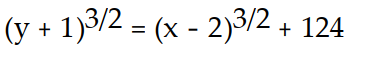
C)
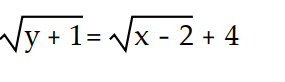
D)
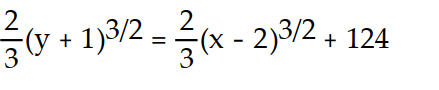
-
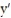 (x)
(x) 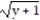 =
= 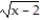 , y( 3) = 24
, y( 3) = 24A)
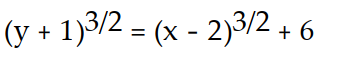
B)
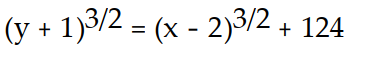
C)
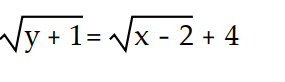
D)
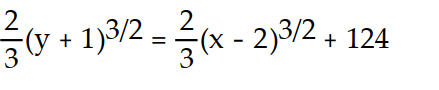

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the initial value problem and leave the solution in implicit form.
-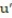 (x) = sec u sin
(x) = sec u sin 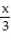 , u( 6 ) =
, u( 6 ) =
A)
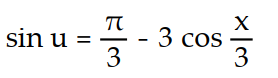
B)
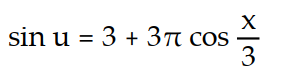
C)
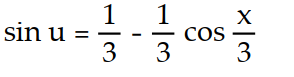
D)
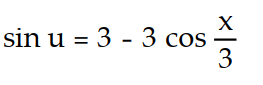
-
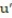 (x) = sec u sin
(x) = sec u sin 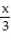 , u( 6 ) =
, u( 6 ) = A)
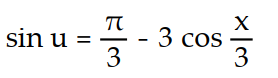
B)
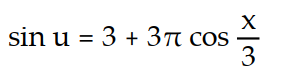
C)
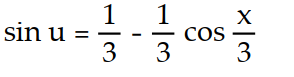
D)
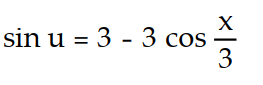

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
-The spread of a cold virus can be modeled using logistic equations. The key assumption is that at any given time, a fraction y of the population, where 0 ≤ y ≤ 1, has the virus, while the remaining fraction 1-y does not. Furthermore, the cold virus spreads by interactions between those who have it and those who do not. The number of such interactions is proportional to y(1 - y). Therefore, the equation that describes the spread of the virus is where k is a positive real number. Assume k = 0.7 and solve the initial value problem where the number of people who initially have the cold virus is y(0) = 0.3
where k is a positive real number. Assume k = 0.7 and solve the initial value problem where the number of people who initially have the cold virus is y(0) = 0.3
A) y =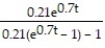
B) y =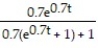
C) y =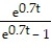
D) y =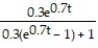
-The spread of a cold virus can be modeled using logistic equations. The key assumption is that at any given time, a fraction y of the population, where 0 ≤ y ≤ 1, has the virus, while the remaining fraction 1-y does not. Furthermore, the cold virus spreads by interactions between those who have it and those who do not. The number of such interactions is proportional to y(1 - y). Therefore, the equation that describes the spread of the virus is
 where k is a positive real number. Assume k = 0.7 and solve the initial value problem where the number of people who initially have the cold virus is y(0) = 0.3
where k is a positive real number. Assume k = 0.7 and solve the initial value problem where the number of people who initially have the cold virus is y(0) = 0.3A) y =
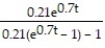
B) y =
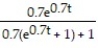
C) y =
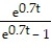
D) y =
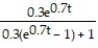

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
-Let y(t) be the concentration of a substance in a chemical reaction. The change in the concentration, under appropriate conditions, is modeled by the equation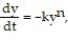 where k > 0 is a rate constant and the positive integer n is the order of the reaction. Solve the initial value problem for a third-order reaction
where k > 0 is a rate constant and the positive integer n is the order of the reaction. Solve the initial value problem for a third-order reaction 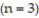 , assuming y(0) = 4 and k = 0.6.
, assuming y(0) = 4 and k = 0.6.
A) y =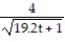
B) y = -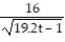
C) y =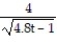
D) y =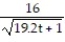
-Let y(t) be the concentration of a substance in a chemical reaction. The change in the concentration, under appropriate conditions, is modeled by the equation
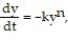 where k > 0 is a rate constant and the positive integer n is the order of the reaction. Solve the initial value problem for a third-order reaction
where k > 0 is a rate constant and the positive integer n is the order of the reaction. Solve the initial value problem for a third-order reaction 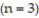 , assuming y(0) = 4 and k = 0.6.
, assuming y(0) = 4 and k = 0.6.A) y =
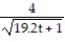
B) y = -
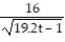
C) y =
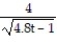
D) y =
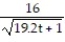

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Find the general solution of the equation.
-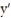 (t) + 2y = 11
(t) + 2y = 11
A) y =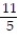 +
+ 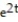
B) y =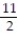 + C
+ C 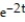
C) y = 11 + C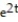
D) y =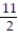 +
+ 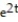 + C
+ C 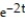
-
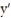 (t) + 2y = 11
(t) + 2y = 11A) y =
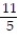 +
+ 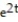
B) y =
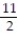 + C
+ C 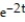
C) y = 11 + C
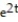
D) y =
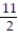 +
+ 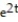 + C
+ C 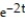

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
Find the general solution of the equation.
-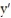 (x) = y - 4
(x) = y - 4
A) y =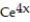 - 4
- 4
B) y =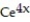
C) y =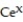 - 4
- 4
D) y =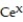 + 4
+ 4
-
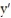 (x) = y - 4
(x) = y - 4A) y =
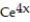 - 4
- 4B) y =
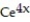
C) y =
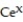 - 4
- 4D) y =
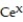 + 4
+ 4
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
Find the general solution of the equation.
-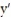 (t) -
(t) - 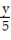 = -8
= -8
A)
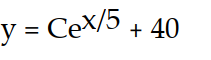
B)
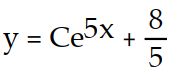
C)
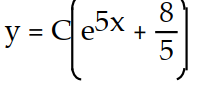
D)
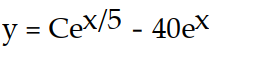
-
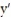 (t) -
(t) - 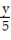 = -8
= -8A)
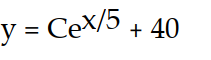
B)
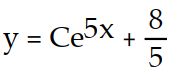
C)
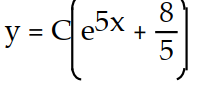
D)
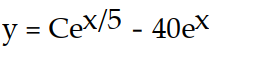

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Find the general solution of the equation.
-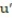 (x) = 10u + 11
(x) = 10u + 11
A)
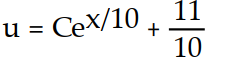
B)
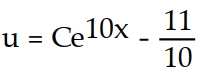
C)
D)
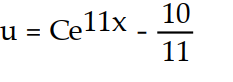
-
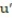 (x) = 10u + 11
(x) = 10u + 11A)
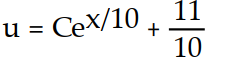
B)
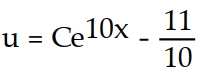
C)
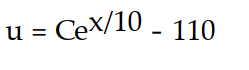
D)
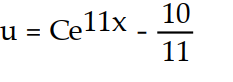

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the initial value problem.
-y'(t) + 9y = 3, y(0) = 1
A)
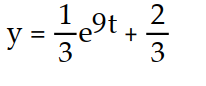
B)
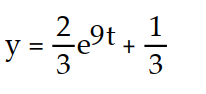
C)
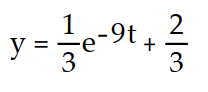
D)
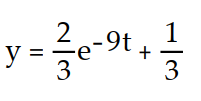
-y'(t) + 9y = 3, y(0) = 1
A)
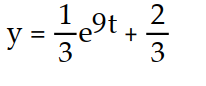
B)
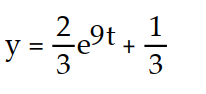
C)
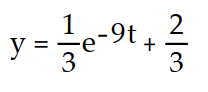
D)
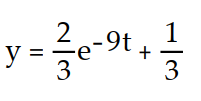

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the initial value problem.
- (t) = 4y - 8, y(0) = 11
(t) = 4y - 8, y(0) = 11
A)
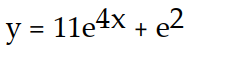
B)
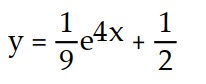
C)
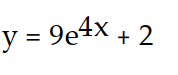
D)
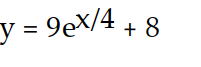
-
 (t) = 4y - 8, y(0) = 11
(t) = 4y - 8, y(0) = 11A)
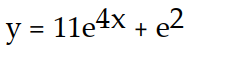
B)
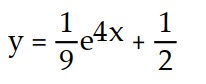
C)
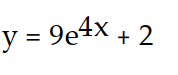
D)
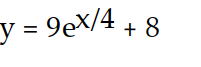

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the initial value problem.
-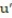 (x) = 3u + 12, u(1) = -2
(x) = 3u + 12, u(1) = -2
A)
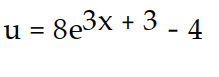
B)
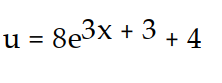
C)
D)
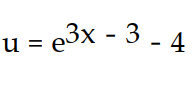
-
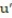 (x) = 3u + 12, u(1) = -2
(x) = 3u + 12, u(1) = -2A)
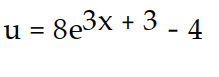
B)
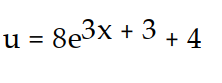
C)
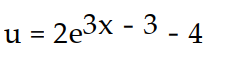
D)
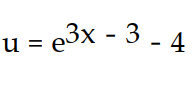

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the initial value problem.
-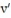 (t)+
(t)+ 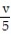 = 7, v(-1) = 0
= 7, v(-1) = 0
A)
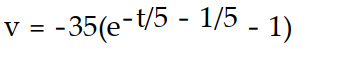
B)
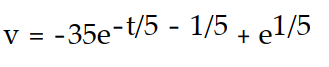
C)
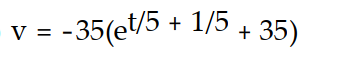
D)
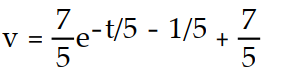
-
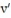 (t)+
(t)+ 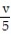 = 7, v(-1) = 0
= 7, v(-1) = 0A)
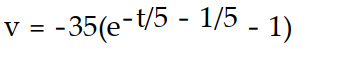
B)
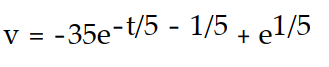
C)
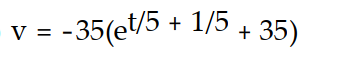
D)
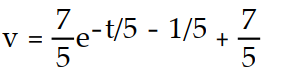

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
Find the equilibrium solution of the equation. Use a sketch of the direction field for 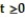 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable
-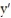 (t) = 7y - 16
(t) = 7y - 16
A) y =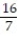 ; stable
; stable
B) y = 23; stable
C) y =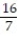 ; unstable
; unstable
D) y =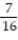 ; unstable
; unstable
 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable-
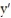 (t) = 7y - 16
(t) = 7y - 16A) y =
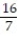 ; stable
; stableB) y = 23; stable
C) y =
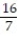 ; unstable
; unstableD) y =
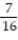 ; unstable
; unstable
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
Find the equilibrium solution of the equation. Use a sketch of the direction field for 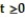 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable
-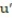 (t) +
(t) +  = -1
= -1
A) u = -6; stable
B) u = 6; unstable
C) u =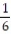 ; unstable
; unstable
D) u =-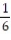 ; stable
; stable
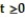 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable-
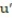 (t) +
(t) +  = -1
= -1A) u = -6; stable
B) u = 6; unstable
C) u =
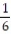 ; unstable
; unstableD) u =-
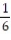 ; stable
; stable
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
Find the equilibrium solution of the equation. Use a sketch of the direction field for 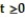 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable
-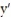 (t) + 2u + 8 = 0
(t) + 2u + 8 = 0
A) y = - ; stable
; stable
B) y = -4; unstable
C) y = 4; stable
D) y = ; unstable
; unstable
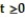 to determine whether the equilibrium is stable
to determine whether the equilibrium is stable-
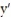 (t) + 2u + 8 = 0
(t) + 2u + 8 = 0A) y = -
 ; stable
; stableB) y = -4; unstable
C) y = 4; stable
D) y =
 ; unstable
; unstable
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
-Use Newton's Law of Cooling to find the temperature in the following case. A loaf of bread is removed from an oven at and cooled in a room whose temperature is
and cooled in a room whose temperature is 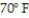 . If the bread cools to
. If the bread cools to 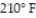 in 20 minutes, how much longer will it take the bread to cool to
in 20 minutes, how much longer will it take the bread to cool to 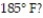
A) 18 minutes
B) 6 minutes
C) 26 minutes
D) 7 minutes
-Use Newton's Law of Cooling to find the temperature in the following case. A loaf of bread is removed from an oven at
 and cooled in a room whose temperature is
and cooled in a room whose temperature is 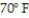 . If the bread cools to
. If the bread cools to 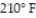 in 20 minutes, how much longer will it take the bread to cool to
in 20 minutes, how much longer will it take the bread to cool to 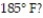
A) 18 minutes
B) 6 minutes
C) 26 minutes
D) 7 minutes

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
-The initial value problem models the payoff of a loan. Solve the initial value problem for t 0, and determine the first month in which the balance is zero. (t) = 0.01B - 2000, B(0) = 100,000
(t) = 0.01B - 2000, B(0) = 100,000
A) B = 20,000 - 10,000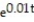 , reaches a balance of zero after approximately 59 months
, reaches a balance of zero after approximately 59 months
B) B = 20,000 + 10,000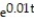 , reaches a balance of zero after approximately 79 months
, reaches a balance of zero after approximately 79 months
C) B = 200,000,000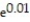 + 20,000,000
+ 20,000,000 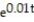 , reaches a balance of zero after approximately 119 months
, reaches a balance of zero after approximately 119 months
D) B = 200,000 - 100,000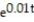 , reaches a balance of zero after approximately 69 months
, reaches a balance of zero after approximately 69 months
-The initial value problem models the payoff of a loan. Solve the initial value problem for t 0, and determine the first month in which the balance is zero.
 (t) = 0.01B - 2000, B(0) = 100,000
(t) = 0.01B - 2000, B(0) = 100,000A) B = 20,000 - 10,000
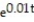 , reaches a balance of zero after approximately 59 months
, reaches a balance of zero after approximately 59 monthsB) B = 20,000 + 10,000
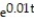 , reaches a balance of zero after approximately 79 months
, reaches a balance of zero after approximately 79 monthsC) B = 200,000,000
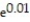 + 20,000,000
+ 20,000,000 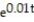 , reaches a balance of zero after approximately 119 months
, reaches a balance of zero after approximately 119 monthsD) B = 200,000 - 100,000
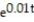 , reaches a balance of zero after approximately 69 months
, reaches a balance of zero after approximately 69 months
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
-Use Newton's Law of Cooling to find the temperature in the following case. A glass of water with a temperature of 6°C is placed in a room with a temperature of 30°C. One minute later the water has warmed to 9°C. After how many minutes does the water have a temperature that is 90% of the ambient temperature?
A) 23 min
B) 16 min
C) 19 min
D) 27 min
-Use Newton's Law of Cooling to find the temperature in the following case. A glass of water with a temperature of 6°C is placed in a room with a temperature of 30°C. One minute later the water has warmed to 9°C. After how many minutes does the water have a temperature that is 90% of the ambient temperature?
A) 23 min
B) 16 min
C) 19 min
D) 27 min

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
-Let y(t) be the population of a species of plant that is being harvested, for t ≥ 0. Consider the harvesting model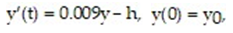 where h is the annual harvesting rate, y0 is the initial population of the species, and t is measured in years. If y0 = 5000, what harvesting rate should be used to maintain a constant population of y = 5000, for t ≥ 0?
where h is the annual harvesting rate, y0 is the initial population of the species, and t is measured in years. If y0 = 5000, what harvesting rate should be used to maintain a constant population of y = 5000, for t ≥ 0?
A) h = 5000
B) h = 25
C) h = 450
D) h = 45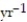
-Let y(t) be the population of a species of plant that is being harvested, for t ≥ 0. Consider the harvesting model
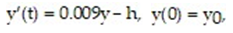 where h is the annual harvesting rate, y0 is the initial population of the species, and t is measured in years. If y0 = 5000, what harvesting rate should be used to maintain a constant population of y = 5000, for t ≥ 0?
where h is the annual harvesting rate, y0 is the initial population of the species, and t is measured in years. If y0 = 5000, what harvesting rate should be used to maintain a constant population of y = 5000, for t ≥ 0? A) h = 5000
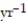
B) h = 25
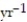
C) h = 450
D) h = 45
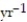

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
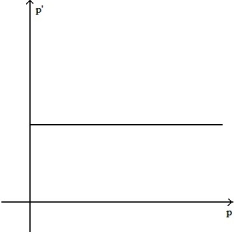
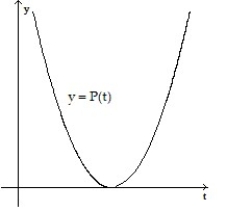
Make a sketch of the population function (as a function of time) that results from the given growth rate function. Assume the population at time t = 0 begins at some positive value.
-
A)
B)
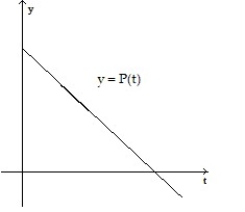
C)
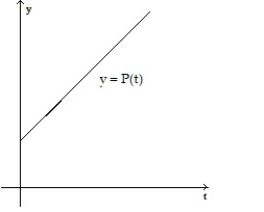
D)
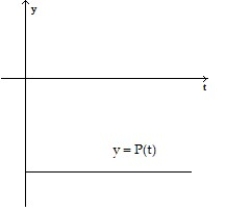
-

A)

B)

C)

D)
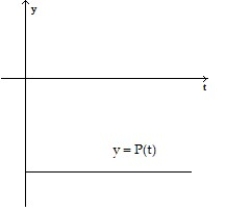

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
Make a sketch of the population function (as a function of time) that results from the given growth rate function. Assume the population at time t = 0 begins at some positive value.
-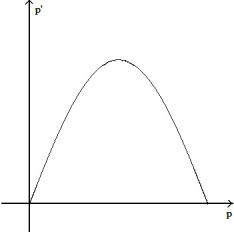
A)
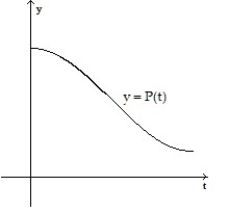
B)
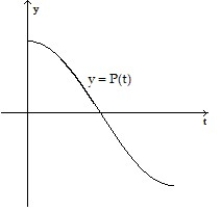
C)
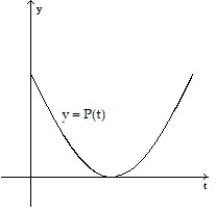
D)
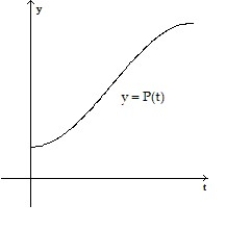
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
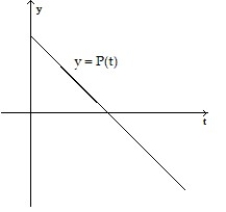
Make a sketch of the population function (as a function of time) that results from the given growth rate function. Assume the population at time t = 0 begins at some positive value.
-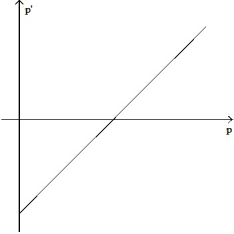
A)
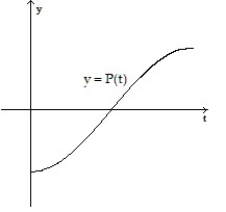
B)
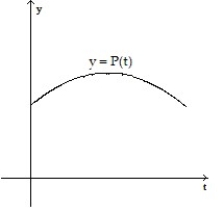
C)
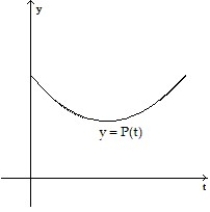
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
Write a logistic equation with the given parameter values. Then solve the initial value problem and graph the solution. Let r be the natural growth rate, K the carrying capacity, and  the initial population.
the initial population.
-r = 0.2, K = 1680,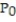 = 80
= 80
A)
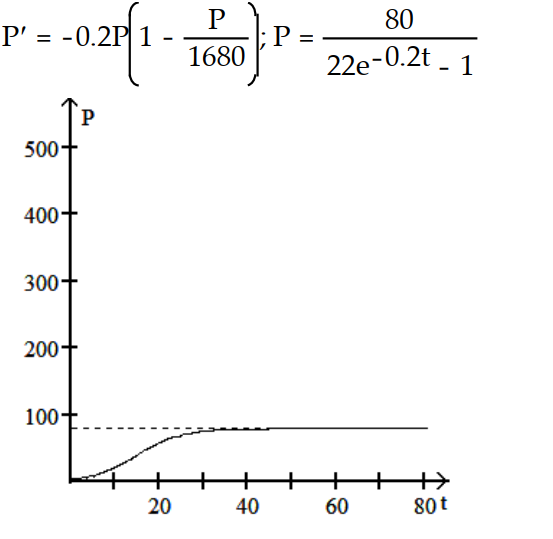
B)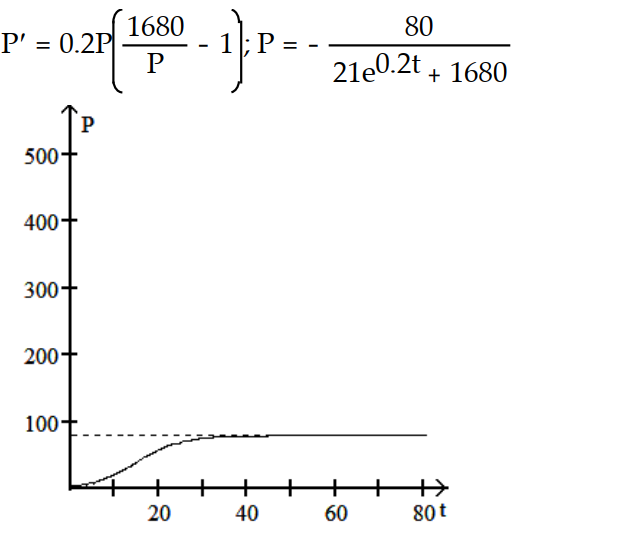
C)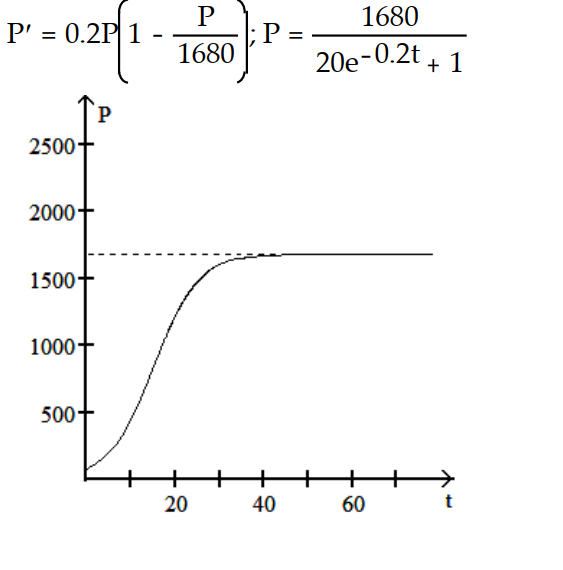
D)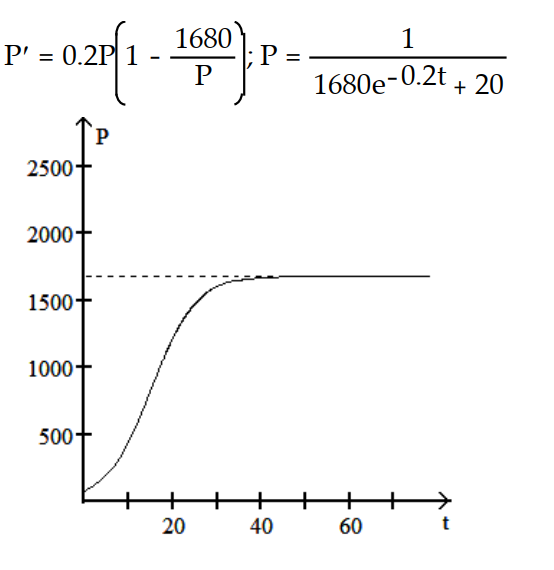
 the initial population.
the initial population.-r = 0.2, K = 1680,
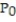 = 80
= 80 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
Write a logistic equation with the given parameter values. Then solve the initial value problem and graph the solution. Let r be the natural growth rate, K the carrying capacity, and  the initial population.
the initial population.
-r = 0.9, K = 7670,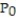 = 590
= 590
A)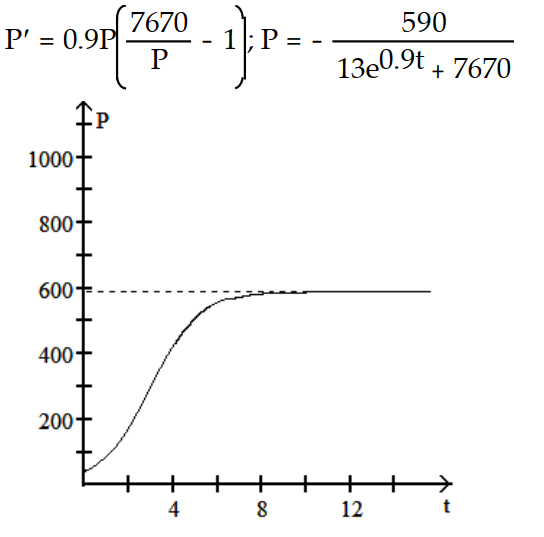
B)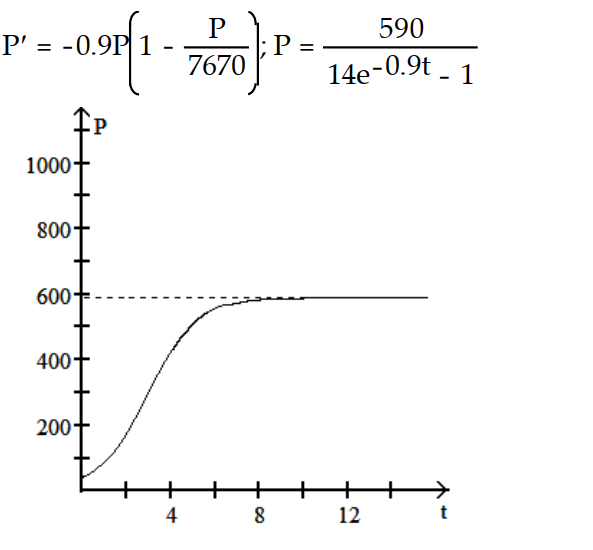
C)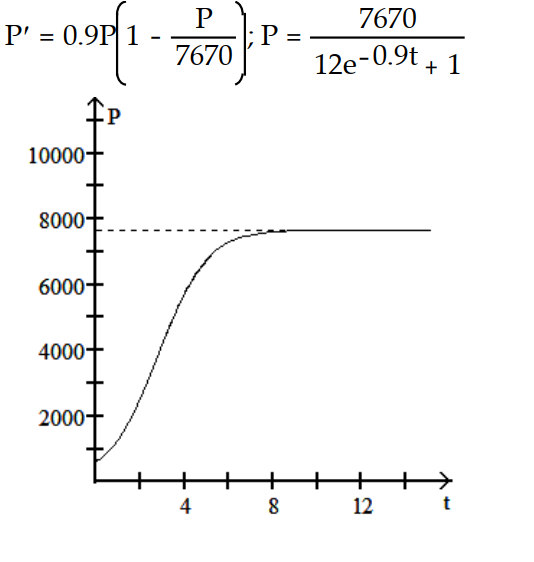
D)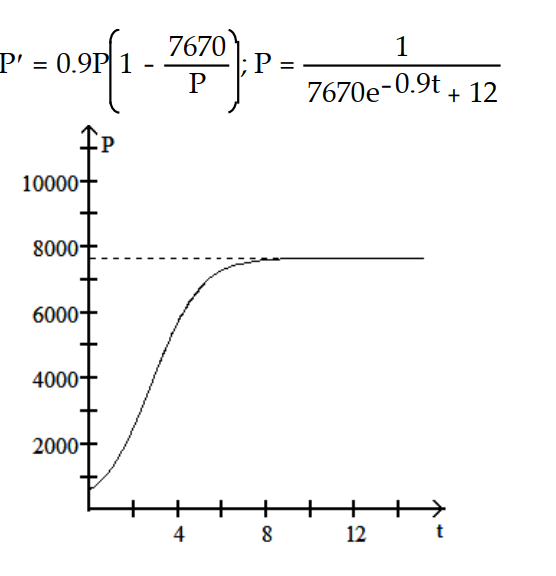
 the initial population.
the initial population.-r = 0.9, K = 7670,
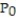 = 590
= 590 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
Find a logistic function that describes the population. Graph the population function.
-The population increases from 300 to 600 in the first year and eventually levels off at 2100.
A)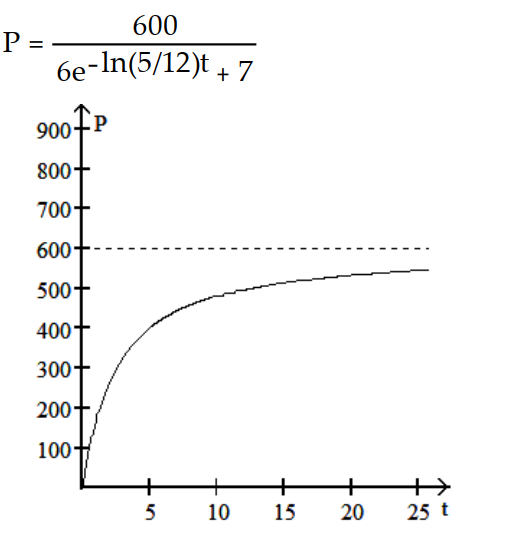
B)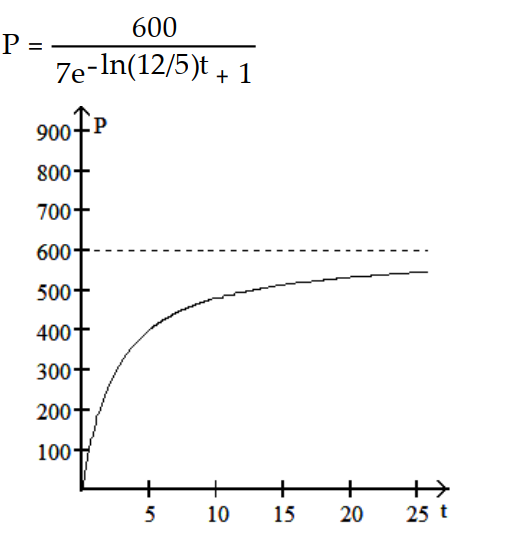
C)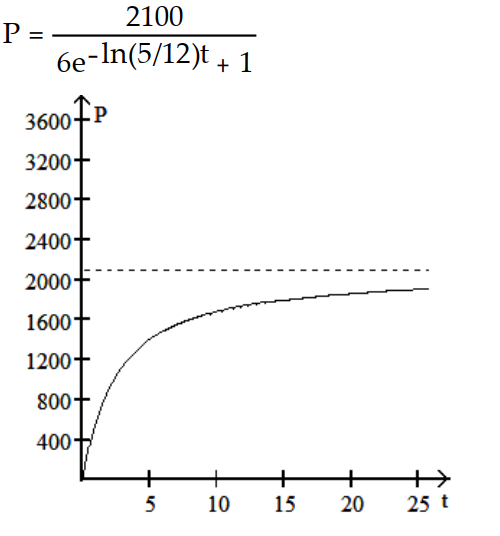
D)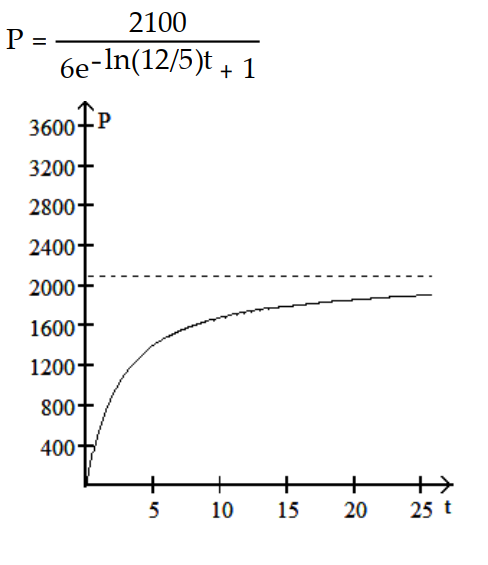
-The population increases from 300 to 600 in the first year and eventually levels off at 2100.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Find a logistic function that describes the population. Graph the population function.
-The population increases from 50 to 70 in the first month and eventually levels off at 150.
A)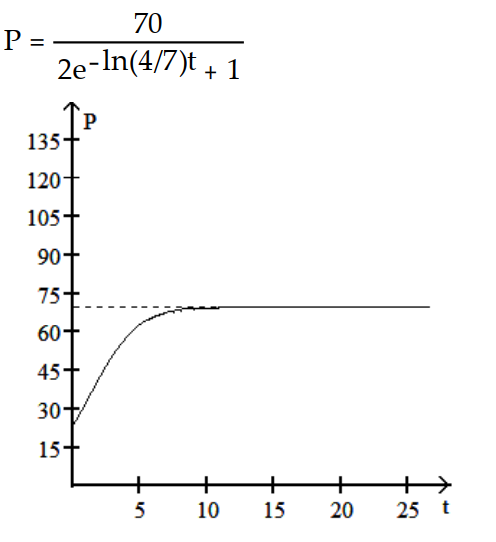
B)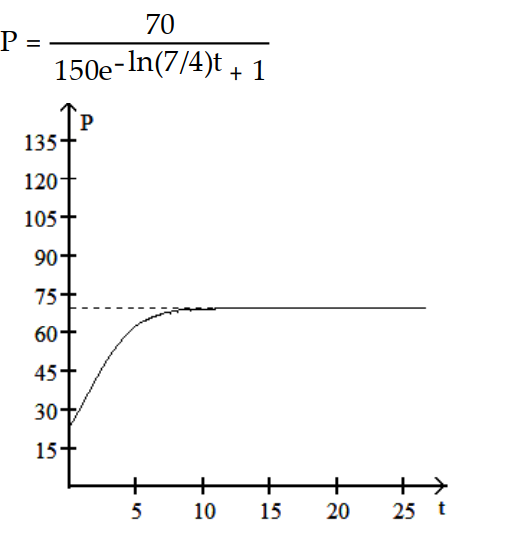
C)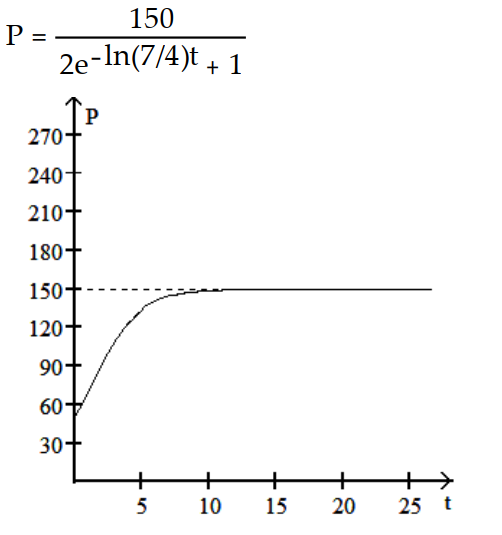
D)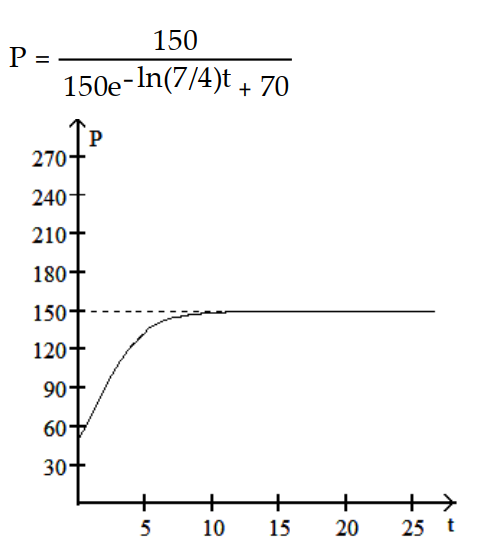
-The population increases from 50 to 70 in the first month and eventually levels off at 150.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
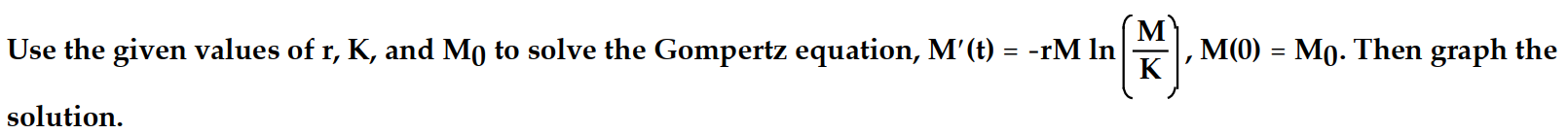
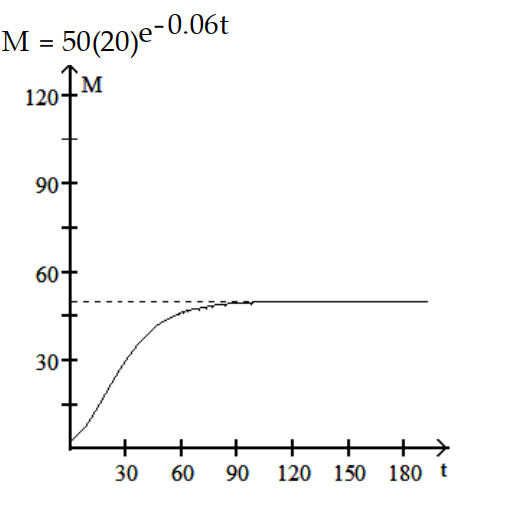
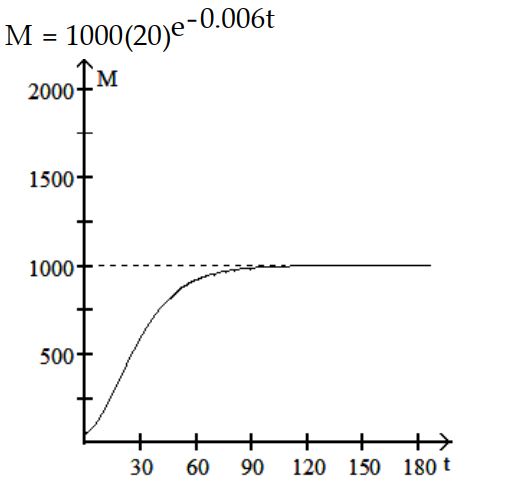
-r = 0.06, K = 1000,
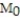 = 50
= 50 
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
-A 500 gallon tank is filled with pure water. A salt solution with a concentration of 11 g/gal flows into the tank at a rate of 7 gal/min. The thoroughly mixed solution is drained from the tank at a rate of 7 gal/min.
(a) Write an initial value problem for the mass of the salt.
(b) Solve the initial value problem.
A)
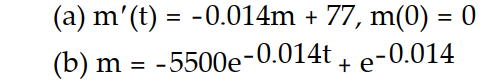
B)
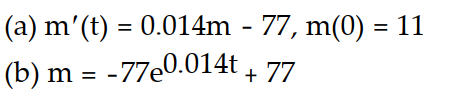
C)
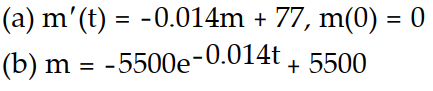
D)
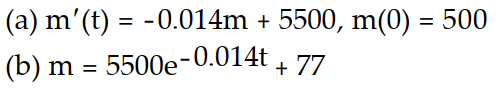
-A 500 gallon tank is filled with pure water. A salt solution with a concentration of 11 g/gal flows into the tank at a rate of 7 gal/min. The thoroughly mixed solution is drained from the tank at a rate of 7 gal/min.
(a) Write an initial value problem for the mass of the salt.
(b) Solve the initial value problem.
A)
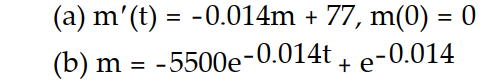
B)
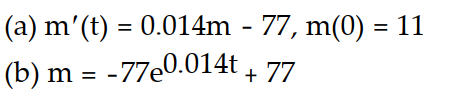
C)
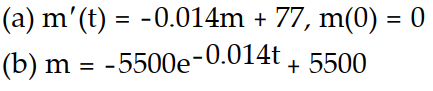
D)
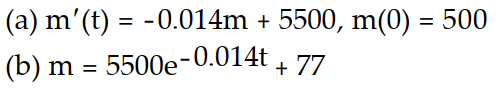

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
-A 2000-L tank is initially filled with a copper sulfate solution with a concentration of 30 g/L. A copper sulfate solution with a concentration of 20 g/L flows into the tank at a rate of 6 L/min. The thoroughly mixed solution is drained from the tank at a rate of 6 L/min.
(a) Write an initial value problem for the mass of the copper sulfate.
(b) Solve the initial value problem.
A)
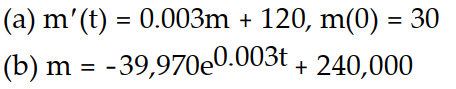
B)
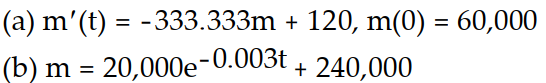
C)
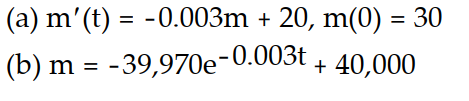
D)
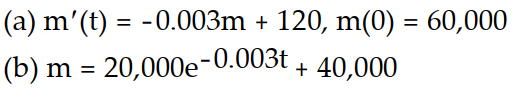
-A 2000-L tank is initially filled with a copper sulfate solution with a concentration of 30 g/L. A copper sulfate solution with a concentration of 20 g/L flows into the tank at a rate of 6 L/min. The thoroughly mixed solution is drained from the tank at a rate of 6 L/min.
(a) Write an initial value problem for the mass of the copper sulfate.
(b) Solve the initial value problem.
A)
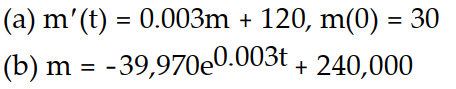
B)
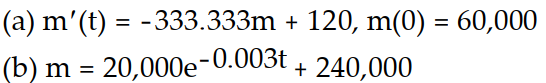
C)
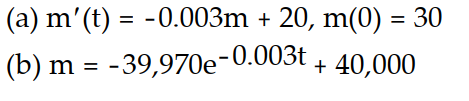
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
-Consider the pair of differential equations that model a predator-prey system with populations x and y.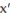 (t) = 3x - 6xy
(t) = 3x - 6xy
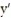 (t) = -y + 7xy
(t) = -y + 7xy
(a) Find the lines along which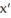 (t) = 0,
(t) = 0,
(b) find the lines along which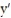 (t) = 0,
(t) = 0,
(c) find the equilibrium points for the system.
A)
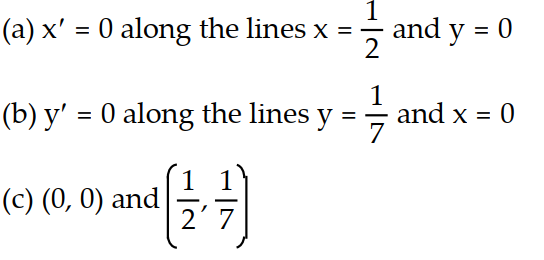
B)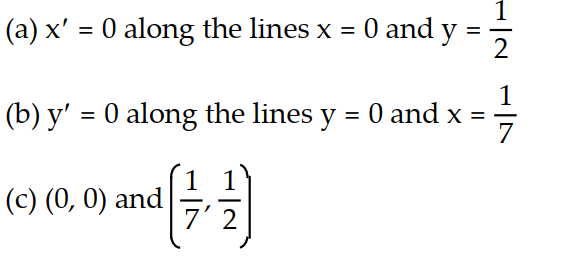
C)
D)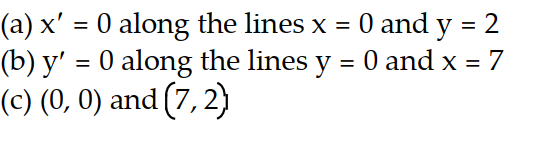
-Consider the pair of differential equations that model a predator-prey system with populations x and y.
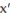 (t) = 3x - 6xy
(t) = 3x - 6xy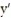 (t) = -y + 7xy
(t) = -y + 7xy(a) Find the lines along which
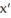 (t) = 0,
(t) = 0,(b) find the lines along which
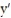 (t) = 0,
(t) = 0,(c) find the equilibrium points for the system.
A)
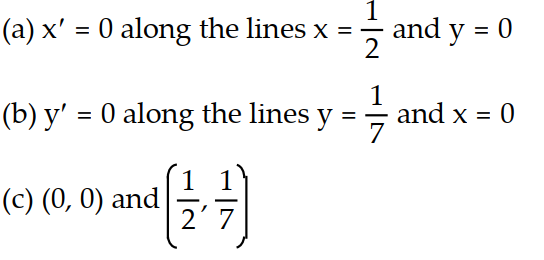
B)
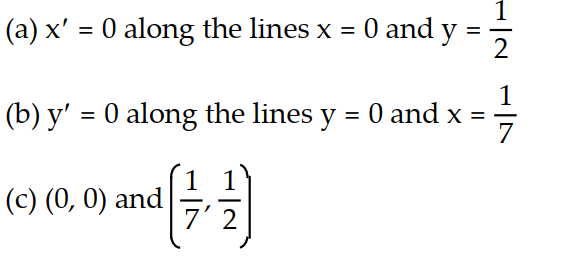
C)
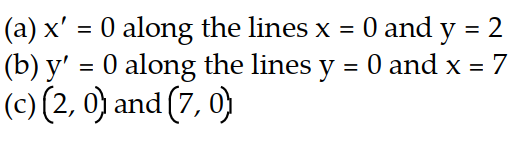
D)
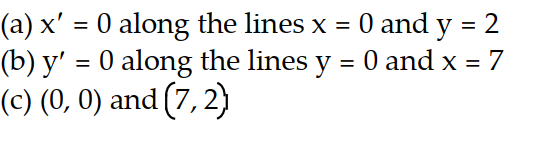

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the problem.
-Consider the pair of differential equations that model a predator-prey system with populations x and y.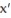 (t) = 5x - xy
(t) = 5x - xy
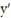 (t) = -3y + xy
(t) = -3y + xy
(a) Find the lines along which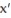 (t) = 0,
(t) = 0,
(b) find the lines along which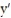 (t) = 0,
(t) = 0,
(c) find the equilibrium points for the system.
A)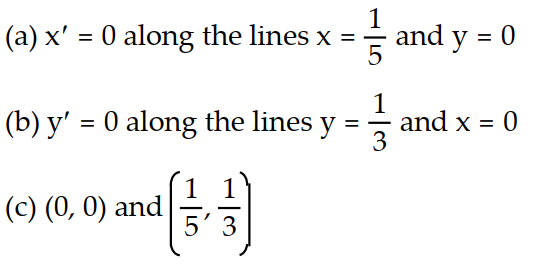
B)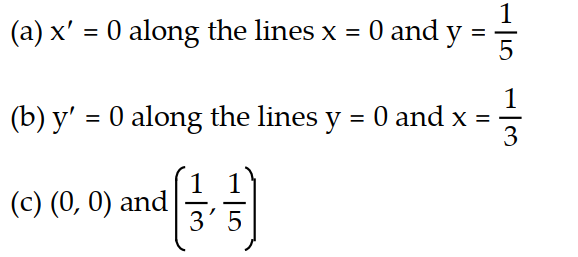
C)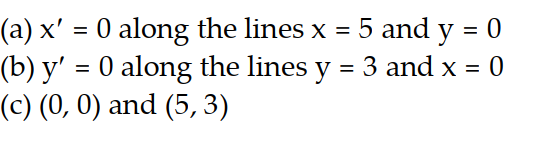
D)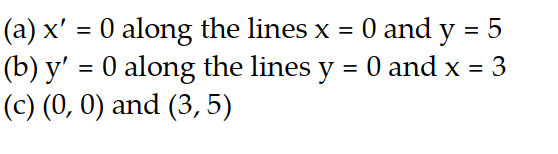
-Consider the pair of differential equations that model a predator-prey system with populations x and y.
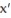 (t) = 5x - xy
(t) = 5x - xy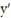 (t) = -3y + xy
(t) = -3y + xy(a) Find the lines along which
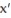 (t) = 0,
(t) = 0,(b) find the lines along which
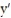 (t) = 0,
(t) = 0,(c) find the equilibrium points for the system.
A)
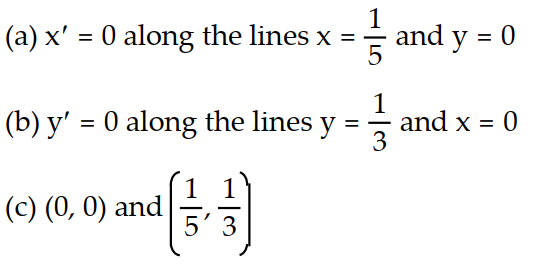
B)
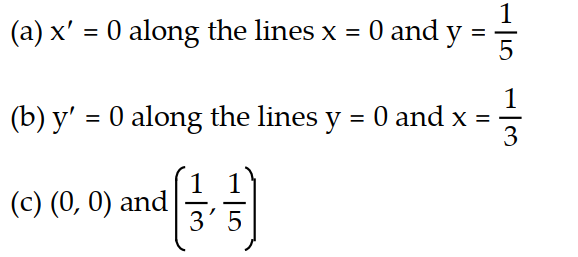
C)
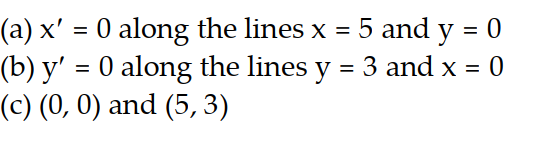
D)
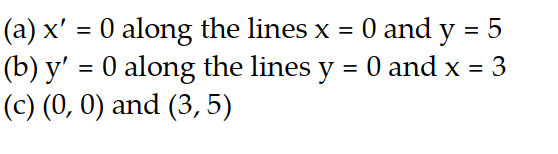

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
-According to a country's census, the population (to the nearest million) was 266 in Year 0 and 306 in Year 10. The projected population for Year 50 is 445. To construct a logistic model, both the growth and carrying capacity must be estimated.
(a) Estimate r by assuming that t = 0 corresponds to Year 0 and that the population between Year 0 and Year 10 is exponential; that is, the population is given by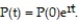 Round the value of r to four decimal places, if necessary.
Round the value of r to four decimal places, if necessary.
(b) Write the solution to the logistic equation using the estimated value of r and use the projected value P(50) = 445 million to find an estimation for the value of the carrying capacity K. Round to the nearest million.
A)
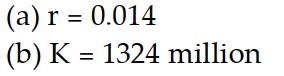
B)
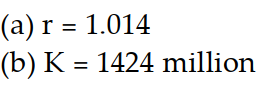
C)
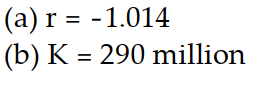
D)
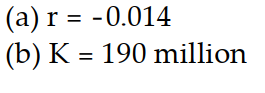
-According to a country's census, the population (to the nearest million) was 266 in Year 0 and 306 in Year 10. The projected population for Year 50 is 445. To construct a logistic model, both the growth and carrying capacity must be estimated.
(a) Estimate r by assuming that t = 0 corresponds to Year 0 and that the population between Year 0 and Year 10 is exponential; that is, the population is given by
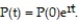 Round the value of r to four decimal places, if necessary.
Round the value of r to four decimal places, if necessary.(b) Write the solution to the logistic equation using the estimated value of r and use the projected value P(50) = 445 million to find an estimation for the value of the carrying capacity K. Round to the nearest million.
A)
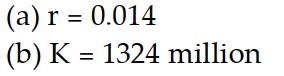
B)
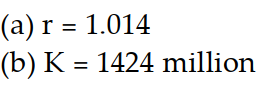
C)
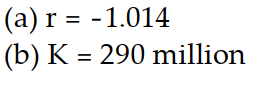
D)
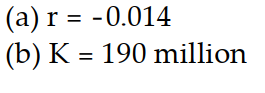

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


