Deck 8: Integration Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/287
Play
Full screen (f)
Deck 8: Integration Techniques
1
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-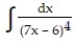
A)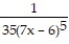 + C
+ C
B) -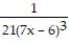 + C
+ C
C) -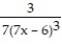 + C
+ C
D)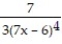 + C
+ C
-
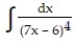
A)
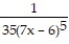 + C
+ CB) -
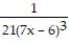 + C
+ CC) -
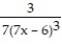 + C
+ CD)
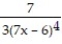 + C
+ C- 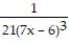 + C
+ C
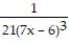 + C
+ C 2
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-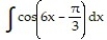
A) -6 sin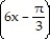 + C
+ C
B) -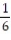 cos
cos 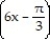 + C
+ C
C) 6 cos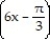 + C
+ C
D)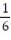 sin
sin 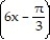 + C
+ C
-
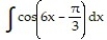
A) -6 sin
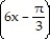 + C
+ CB) -
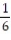 cos
cos 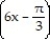 + C
+ CC) 6 cos
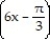 + C
+ CD)
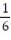 sin
sin 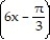 + C
+ C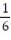 sin
sin 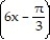 + C
+ C 3
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-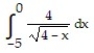
A) 7
B) 2
C) 8
D) 11
-
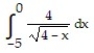
A) 7
B) 2
C) 8
D) 11
8
4
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-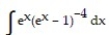
A)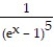 + C
+ C
B)-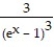 + C
+ C
C)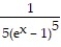 + C
+ C
D) -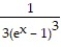 + C
+ C
-
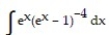
A)
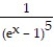 + C
+ CB)-
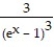 + C
+ CC)
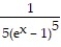 + C
+ CD) -
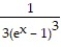 + C
+ C
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
5
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-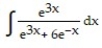
A)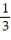 ln
ln 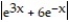 + C
+ C
B) ln
ln 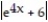 + C
+ C
C) 4 ln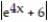 + C
+ C
D) ln
ln 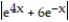 + C
+ C
-
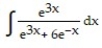
A)
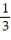 ln
ln 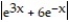 + C
+ CB)
 ln
ln 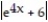 + C
+ CC) 4 ln
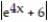 + C
+ CD)
 ln
ln 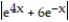 + C
+ C
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
6
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-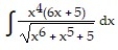
A)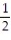
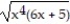 + C
+ C
B) 2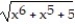 + C
+ C
C)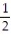
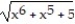 + C
+ C
D) 2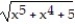 + C
+ C
-
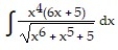
A)
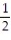
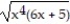 + C
+ CB) 2
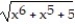 + C
+ CC)
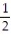
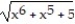 + C
+ CD) 2
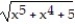 + C
+ C
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
7
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-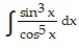
A)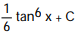
B)
C)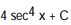
D)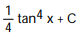
-
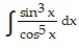
A)
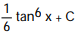
B)

C)
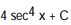
D)
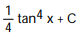

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
8
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-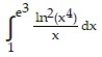
A) 1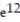
B) 144
C) 2304
D) 144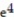
-
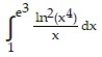
A) 1
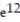
B) 144
C) 2304
D) 144
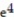

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
9
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-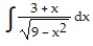
A)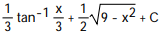
B)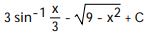
C)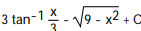
D)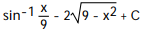
-
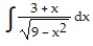
A)
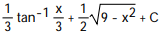
B)
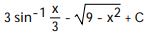
C)
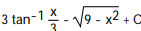
D)
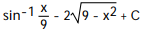

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
10
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-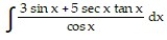
A)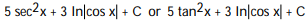
B)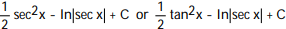
C)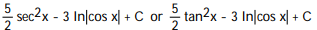
D)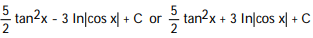
-
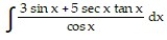
A)
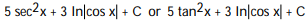
B)
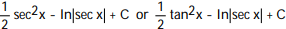
C)
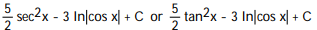
D)
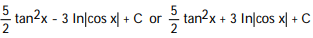

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
11
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-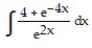
A)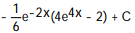
B)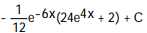
C)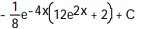
D)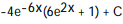
-
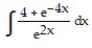
A)
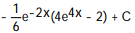
B)
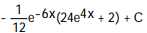
C)
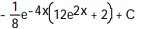
D)
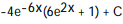

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
12
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-dx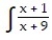
A) x + 8 ln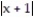 + C
+ C
B) x - 8 ln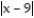 + C
+ C
C) x - 8 ln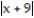 + C
+ C
D)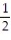 x + 8 ln
x + 8 ln 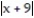 + C
+ C
-dx
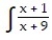
A) x + 8 ln
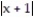 + C
+ CB) x - 8 ln
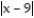 + C
+ CC) x - 8 ln
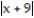 + C
+ CD)
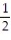 x + 8 ln
x + 8 ln 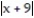 + C
+ C
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
13
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-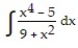
A)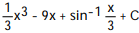
B)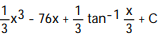
C)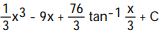
D)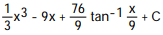
-
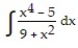
A)
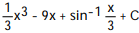
B)
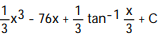
C)
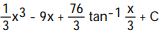
D)
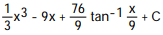

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
14
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-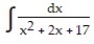
A)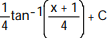
B)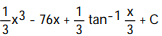
C)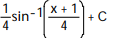
D)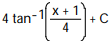
-
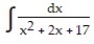
A)
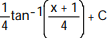
B)
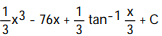
C)
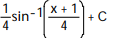
D)
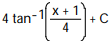

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
15
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-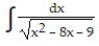
A)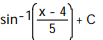
B)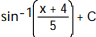
C)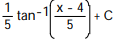
D)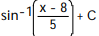
-
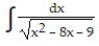
A)
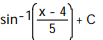
B)
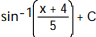
C)
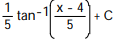
D)
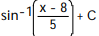

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
16
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-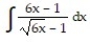
A)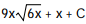
B)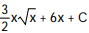
C)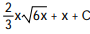
D)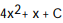
-
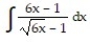
A)
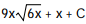
B)
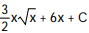
C)
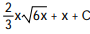
D)
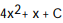

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
17
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-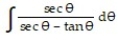
A) tan + sec
B)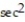 - tan
- tan
C) tan - sec
D)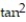 + sec
+ sec
-
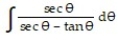
A) tan + sec
B)
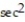 - tan
- tan C) tan - sec
D)
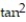 + sec
+ sec 
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the problem.
-Find the area of the entire region bounded by the curves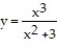 and
and 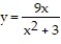
A) 1
B)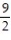 - 6 ln 12
- 6 ln 12
C) 0
D) 9 - 12 ln 12
-Find the area of the entire region bounded by the curves
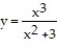 and
and 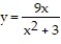
A) 1
B)
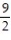 - 6 ln 12
- 6 ln 12C) 0
D) 9 - 12 ln 12

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the problem.
-Consider the region R bounded by the graph of f(x) =![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_035c_bdb6_db3d92bc0e38_TB9662_11.jpg) on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.
on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.
A)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_035d_bdb6_47aba2ea2619_TB9662_11.jpg) + 15
+ 15
B)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a6e_bdb6_477251b26fe0_TB9662_11.jpg)
C)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a6f_bdb6_374246bcce79_TB9662_11.jpg)
D)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a70_bdb6_17d2fd3e9988_TB9662_11.jpg)
-Consider the region R bounded by the graph of f(x) =
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_035c_bdb6_db3d92bc0e38_TB9662_11.jpg) on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.
on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.A)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_035d_bdb6_47aba2ea2619_TB9662_11.jpg) + 15
+ 15B)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a6e_bdb6_477251b26fe0_TB9662_11.jpg)
C)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a6f_bdb6_374246bcce79_TB9662_11.jpg)
D)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the x-axis.</strong> A) + 15 B) C) D)](https://storage.examlex.com/TB9662/11ee9522_343e_2a70_bdb6_17d2fd3e9988_TB9662_11.jpg)

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.
-Consider the region R bounded by the graph of f(x) =![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a71_bdb6_af822298222e_TB9662_11.jpg) on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.
on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.
A)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a72_bdb6_33bb310627b1_TB9662_11.jpg)
B) 2![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a73_bdb6_3d8f70bdf69a_TB9662_11.jpg)
C)![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_5184_bdb6_096d856c0d8e_TB9662_11.jpg)
D) 2![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_5185_bdb6_d5bafaeb8dbf_TB9662_11.jpg)
-Consider the region R bounded by the graph of f(x) =
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a71_bdb6_af822298222e_TB9662_11.jpg) on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.
on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.A)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a72_bdb6_33bb310627b1_TB9662_11.jpg)
B) 2
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_2a73_bdb6_3d8f70bdf69a_TB9662_11.jpg)
C)
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_5184_bdb6_096d856c0d8e_TB9662_11.jpg)
D) 2
![<strong>Solve the problem. -Consider the region R bounded by the graph of f(x) = on the interval [0, 3]. Find the volume of the solid formed when R is revolved about the y-axis.</strong> A) \pi B) 2 \pi C) \pi D) 2 \pi](https://storage.examlex.com/TB9662/11ee9522_343e_5185_bdb6_d5bafaeb8dbf_TB9662_11.jpg)

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the integral.
-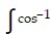 x dx
x dx
A)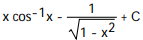
B)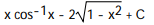
C)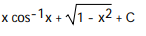
D)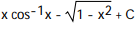
-
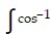 x dx
x dxA)
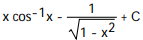
B)
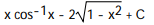
C)
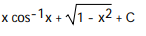
D)
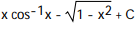

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the integral.
-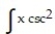 3x dx
3x dx
A)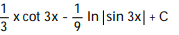
B)
C)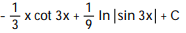
D)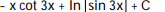
-
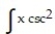 3x dx
3x dxA)
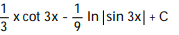
B)

C)
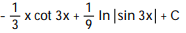
D)
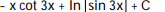

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the integral.
-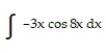
A)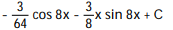
B)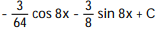
C)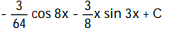
D)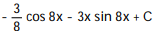
-
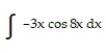
A)
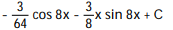
B)
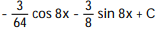
C)
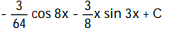
D)
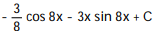

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the integral.
-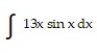
A) 13 sin x - x cos x + C
B) 13 sin x + 13x cos x + C
C) 13 sin x - 13 cos x + C
D) 13 sin x - 13x cos x + C
-
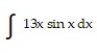
A) 13 sin x - x cos x + C
B) 13 sin x + 13x cos x + C
C) 13 sin x - 13 cos x + C
D) 13 sin x - 13x cos x + C

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the integral.
-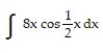
A)
B)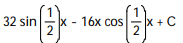
C)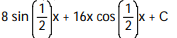
D)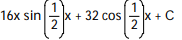
-
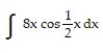
A)

B)
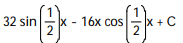
C)
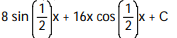
D)
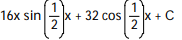

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the integral.
-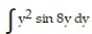
A)
B)
C)
D)
-
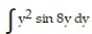
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the integral.
-
A)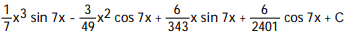
B)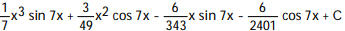
C)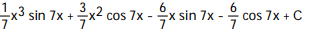
D)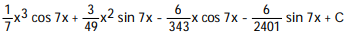
-

A)
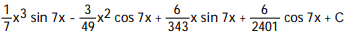
B)
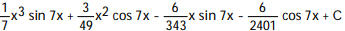
C)
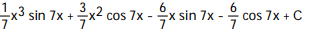
D)
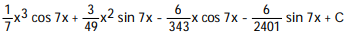

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the integral.
-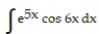
A)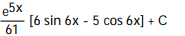
B)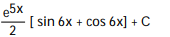
C)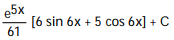
D)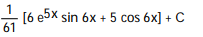
-
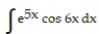
A)
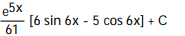
B)
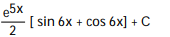
C)
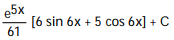
D)
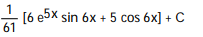

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the integral.
-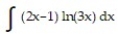
A)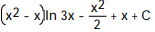
B)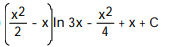
C)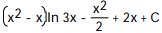
D)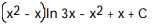
-
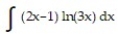
A)
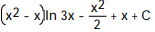
B)
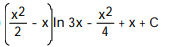
C)
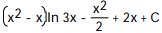
D)
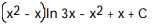

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the integral.
-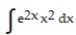
A)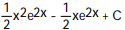
B)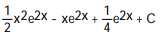
C)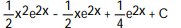
D)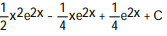
-
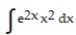
A)
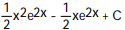
B)
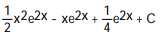
C)
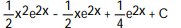
D)
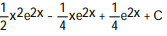

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the integral.
-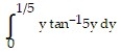 (Give your answer in exact form.)
(Give your answer in exact form.)
A)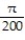 -
- 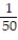
B)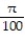 -
- 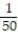
C)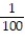
D) -
- 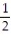
-
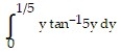 (Give your answer in exact form.)
(Give your answer in exact form.)A)
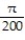 -
- 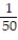
B)
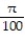 -
- 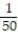
C)
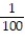
D)
 -
- 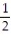

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the integral.
-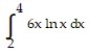
A) 40.2
B) 6.70
C) 55.2
D) 9.48
-
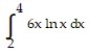
A) 40.2
B) 6.70
C) 55.2
D) 9.48

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the integral.
-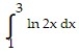
A) 6.68
B) 2.68
C) 4.6
D) 0.68
-
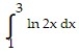
A) 6.68
B) 2.68
C) 4.6
D) 0.68

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the integral.
-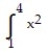 ln 2x dx
ln 2x dx
A) 51.35
B) 37.13
C) 38.91
D) -19.37
-
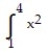 ln 2x dx
ln 2x dx A) 51.35
B) 37.13
C) 38.91
D) -19.37

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the problem.
-Find the volume of the solid generated by revolving the region bounded by the curve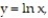 the
the 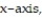 and the vertical line
and the vertical line 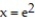 about the x-axis.
about the x-axis.
A) e - 1)
B) 2 (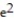 - 1)
- 1)
C) e
D) (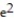 - 1)
- 1)
-Find the volume of the solid generated by revolving the region bounded by the curve
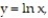 the
the 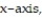 and the vertical line
and the vertical line 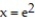 about the x-axis.
about the x-axis.A) e - 1)
B) 2 (
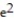 - 1)
- 1)C) e
D) (
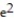 - 1)
- 1)
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
-Find the volume of the solid generated by revolving the region bounded by the curve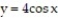 and the
and the 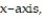
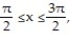 about the x-axis.
about the x-axis.
A) 16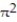
B) 16
C) 8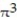
D) 8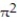
-Find the volume of the solid generated by revolving the region bounded by the curve
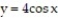 and the
and the 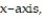
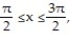 about the x-axis.
about the x-axis.A) 16
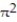
B) 16
C) 8
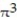
D) 8
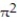

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by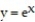 and the
and the 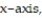 from
from 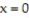 to
to 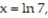 about the
about the 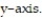
A) 14 ln 7
B) 2 ( 7ln 7 - 7)
C) 2 ( 7ln 7 - 6)
D) 7 ln 7
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by
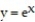 and the
and the 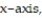 from
from 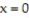 to
to 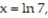 about the
about the 
A) 14 ln 7
B) 2 ( 7ln 7 - 7)
C) 2 ( 7ln 7 - 6)
D) 7 ln 7

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y =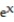 , and the line x = ln 6 about the line x = ln 6.
, and the line x = ln 6 about the line x = ln 6.
A) 2 ( 5 + ln 6)
B) 2 ( 5 - ln 6)
C) 2 ( 6 - ln 6)
D) 2 (6 - ln 7)
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y =
 , and the line x = ln 6 about the line x = ln 6.
, and the line x = ln 6 about the line x = ln 6.A) 2 ( 5 + ln 6)
B) 2 ( 5 - ln 6)
C) 2 ( 6 - ln 6)
D) 2 (6 - ln 7)

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y =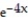 , and the line x = 3 about the y-axis.
, and the line x = 3 about the y-axis.
A)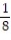 (1 - 11
(1 - 11 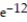 )
)
B)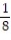 (1 - 12
(1 - 12 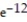 )
)
C) -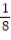 (1 + 13
(1 + 13 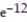 )
)
D)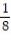 (1 - 13
(1 - 13 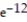 )
)
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the coordinate axes, the curve y =
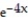 , and the line x = 3 about the y-axis.
, and the line x = 3 about the y-axis.A)
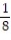 (1 - 11
(1 - 11 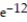 )
)B)
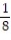 (1 - 12
(1 - 12 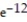 )
)C) -
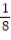 (1 + 13
(1 + 13 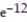 )
)D)
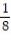 (1 - 13
(1 - 13 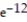 )
)
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the x-axis and the curve y = sin 3x, 0 x / 3 about the line x = / 3.
A)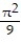
B)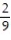
C)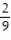
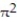
D)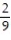
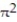 -
-
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the x-axis and the curve y = sin 3x, 0 x / 3 about the line x = / 3.
A)
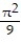
B)
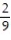
C)
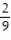
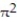
D)
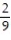
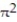 -
- 
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the x-axis and the curve y = x cos x, 0 x /2 about the y-axis.
A)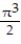 - 8
- 8
B)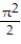 - 4
- 4
C)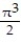 + 2
+ 2 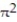 - 4
- 4
D)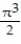 - 4
- 4
-Find the volume of the solid generated by revolving the region in the first quadrant bounded by the x-axis and the curve y = x cos x, 0 x /2 about the y-axis.
A)
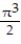 - 8
- 8 B)
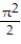 - 4
- 4 C)
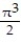 + 2
+ 2 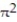 - 4
- 4 D)
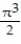 - 4
- 4 
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
42
Use integration by parts to establish a reduction formula for the integral.
-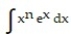
A)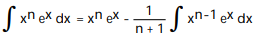
B)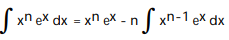
C)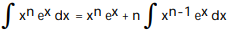
D)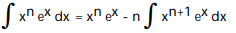
-
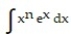
A)
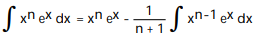
B)
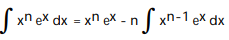
C)
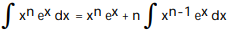
D)
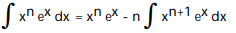

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
43
Use integration by parts to establish a reduction formula for the integral.
-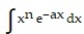
A)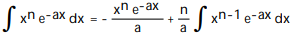
B)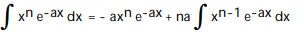
C)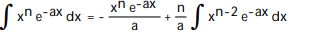
D)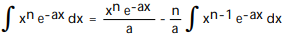
-
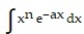
A)
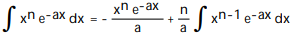
B)
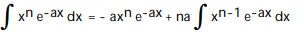
C)
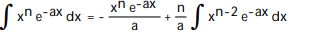
D)
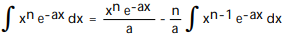

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
44
Use integration by parts to establish a reduction formula for the integral.
-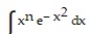
A)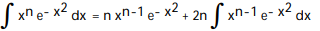
B)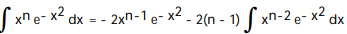
C)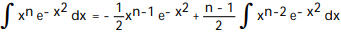
D)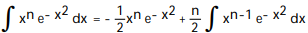
-
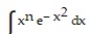
A)
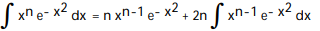
B)
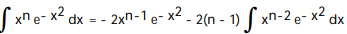
C)
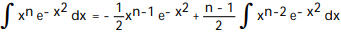
D)
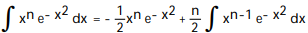

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
45
Use integration by parts to establish a reduction formula for the integral.
-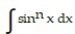
A)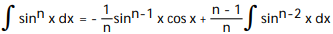
B)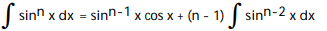
C)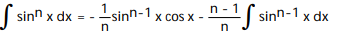
D)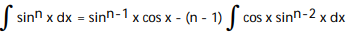
-
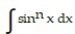
A)
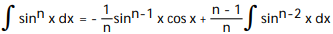
B)
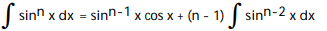
C)
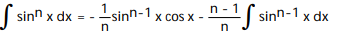
D)
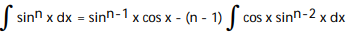

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
46
Use integration by parts to establish a reduction formula for the integral.
-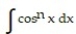
A)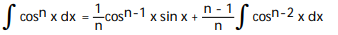
B)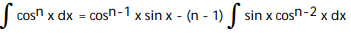
C)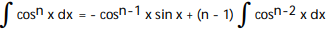
D)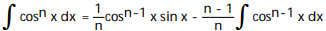
-
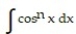
A)
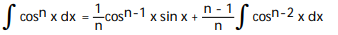
B)
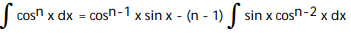
C)
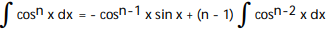
D)
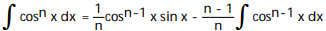

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
47
Use integration by parts to establish a reduction formula for the integral.
-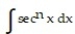 , n 1
, n 1
A)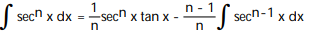
B)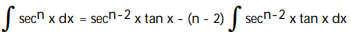
C)
D)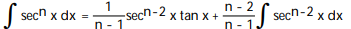
-
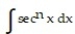 , n 1
, n 1A)
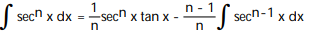
B)
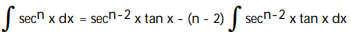
C)

D)
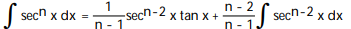

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
48
Use integration by parts to establish a reduction formula for the integral.
-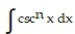 , n 1
, n 1
A)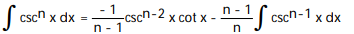
B)
C)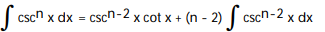
D)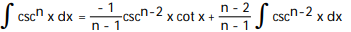
-
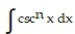 , n 1
, n 1A)
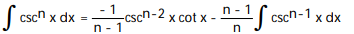
B)

C)
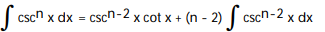
D)
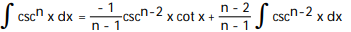

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
49
Use integration by parts to establish a reduction formula for the integral.
-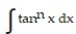 , n 1
, n 1
A)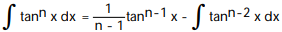
B)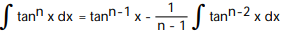
C)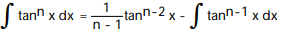
D)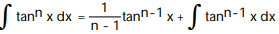
-
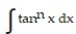 , n 1
, n 1A)
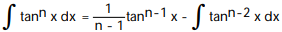
B)
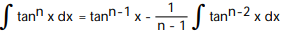
C)
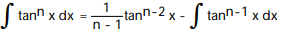
D)
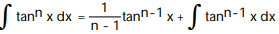

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
50
Use integration by parts to establish a reduction formula for the integral.
-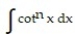 , n 1
, n 1
A)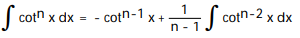
B)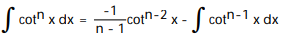
C)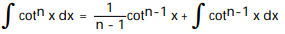
D)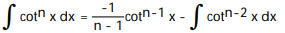
-
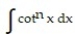 , n 1
, n 1A)
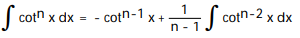
B)
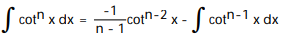
C)
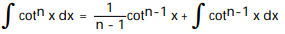
D)
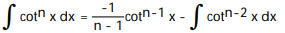

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
51
Use integration by parts to establish a reduction formula for the integral.
-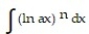
A)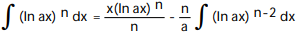
B)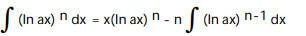
C)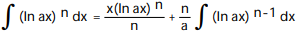
D)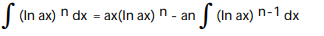
-
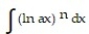
A)
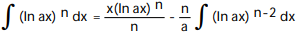
B)
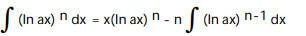
C)
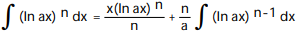
D)
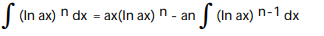

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the integral by using a substitution prior to integration by parts.
-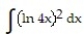
A)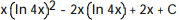
B)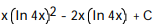
C)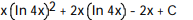
D)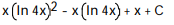
-
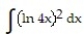
A)
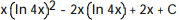
B)
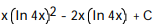
C)
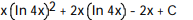
D)
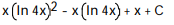

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the integral by using a substitution prior to integration by parts.
-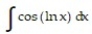
A)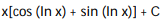
B)
C)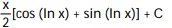
D)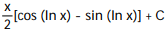
-
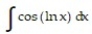
A)
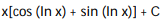
B)

C)
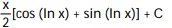
D)
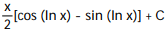

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the integral by using a substitution prior to integration by parts.
-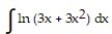
A)
B)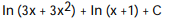
C)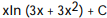
D)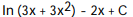
-
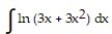
A)

B)
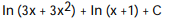
C)
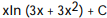
D)
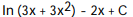

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
-Find the area between y = (x - 2)ex and the x-axis from x = 2 to x = 6.
A) e6 + e2
B) 3e6
C) 3e6 + e2
D) e6 - e2
-Find the area between y = (x - 2)ex and the x-axis from x = 2 to x = 6.
A) e6 + e2
B) 3e6
C) 3e6 + e2
D) e6 - e2

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
-The charge q (in coulombs) delivered by a current i (in amperes) is given by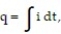 where t is the time (in seconds). A damped-out periodic wave form has current given by
where t is the time (in seconds). A damped-out periodic wave form has current given by 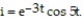 Find a formula for the charge delivered over time t.
Find a formula for the charge delivered over time t.
A)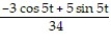 + C
+ C
B)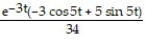 + C
+ C
C)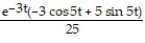 + C
+ C
D)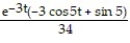 + C
+ C
-The charge q (in coulombs) delivered by a current i (in amperes) is given by
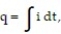 where t is the time (in seconds). A damped-out periodic wave form has current given by
where t is the time (in seconds). A damped-out periodic wave form has current given by 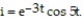 Find a formula for the charge delivered over time t.
Find a formula for the charge delivered over time t.A)
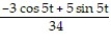 + C
+ CB)
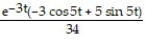 + C
+ CC)
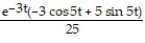 + C
+ CD)
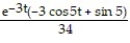 + C
+ C
Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.
-The voltage v (in volts) induced in a tape head is given by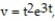 where t is the time (in seconds). Find the average value of v over the interval from t = 0 to t = 4. Round to the nearest volt.
where t is the time (in seconds). Find the average value of v over the interval from t = 0 to t = 4. Round to the nearest volt.
A) 183,853 volts
B) 2,559,851 volts
C) 28,130 volts
D) 30 volts
-The voltage v (in volts) induced in a tape head is given by
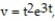 where t is the time (in seconds). Find the average value of v over the interval from t = 0 to t = 4. Round to the nearest volt.
where t is the time (in seconds). Find the average value of v over the interval from t = 0 to t = 4. Round to the nearest volt.A) 183,853 volts
B) 2,559,851 volts
C) 28,130 volts
D) 30 volts

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral.
-
A) 0
B)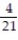
C)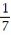
D)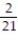
-

A) 0
B)
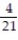
C)
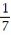
D)
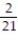

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral.
-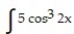 dx
dx
A)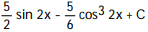
B)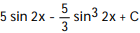
C)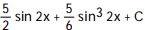
D)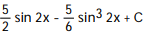
-
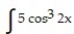 dx
dx A)
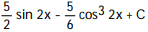
B)
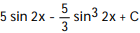
C)
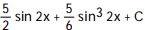
D)
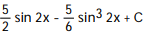

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the integral.
-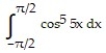
A) 0
B)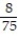
C)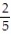
D)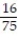
-
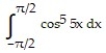
A) 0
B)
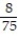
C)
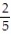
D)
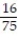

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the integral.
-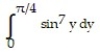
A)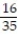
B)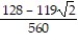
C)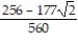
D) -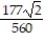
-
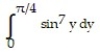
A)
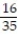
B)
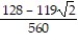
C)
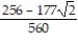
D) -
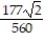

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the integral.
-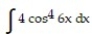
A)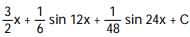
B)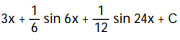
C)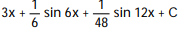
D)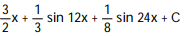
-
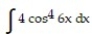
A)
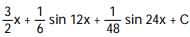
B)
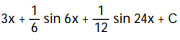
C)
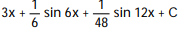
D)
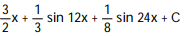

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the integral.
-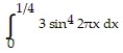
A)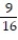
B)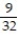 -
- 
C)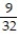
D)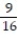 -
- 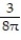
-
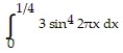
A)
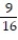
B)
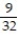 -
- 
C)
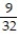
D)
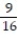 -
- 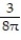

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the integral.
-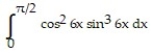
A)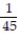
B)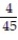
C)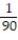
D)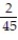
-
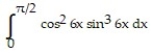
A)
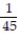
B)
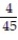
C)
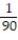
D)
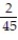

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the integral.
-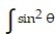 cos 8 d
cos 8 d
A)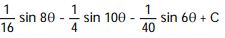
B)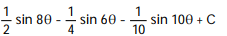
C)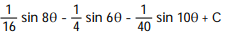
D)
-
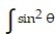 cos 8 d
cos 8 d A)
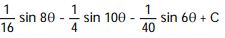
B)
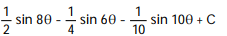
C)
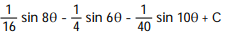
D)


Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the integral.
-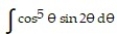
A)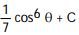
B)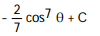
C)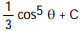
D)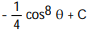
-
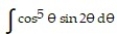
A)
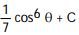
B)
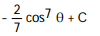
C)
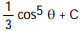
D)
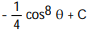

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the integral.
-dx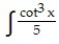
A)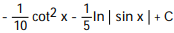
B)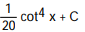
C)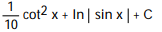
D)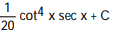
-dx
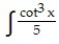
A)
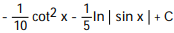
B)
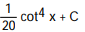
C)
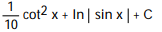
D)
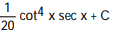

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the integral.
-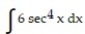
A)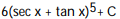
B)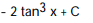
C)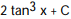
D)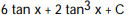
-
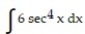
A)
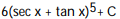
B)
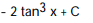
C)
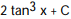
D)
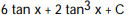

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate the integral.
-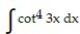
A)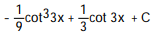
B)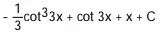
C)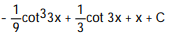
D)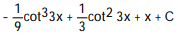
-
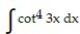
A)
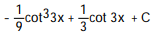
B)
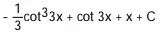
C)
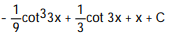
D)
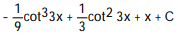

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the integral.
-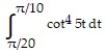
A) -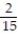
B)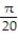 -
- 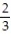
C)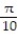 -
- 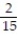
D)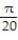 -
- 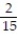
-
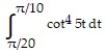
A) -
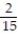
B)
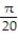 -
- 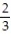
C)
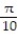 -
- 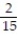
D)
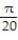 -
- 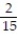

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate the integral.
-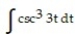
A)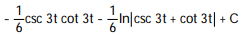
B)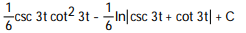
C)
D)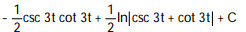
-
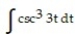
A)
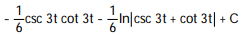
B)
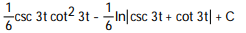
C)

D)
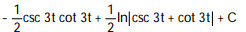

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the integral.
-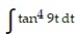
A)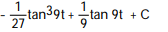
B)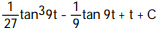
C)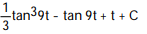
D)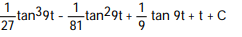
-
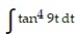
A)
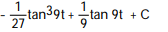
B)
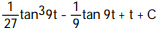
C)
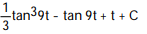
D)
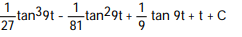

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the integral.
-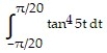
A) -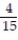
B)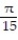 -
- 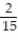
C)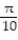
D)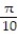 -
- 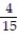
-
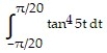
A) -
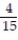
B)
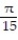 -
- 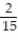
C)
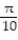
D)
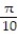 -
- 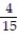

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate the integral.
-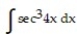
A)
B)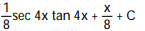
C)
D)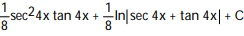
-
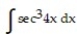
A)

B)
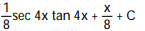
C)

D)
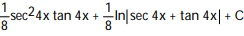

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate the integral.
-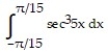 Give your answer in exact form.
Give your answer in exact form.
A)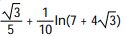
B)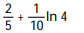
C)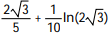
D)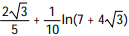
-
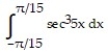 Give your answer in exact form.
Give your answer in exact form.A)
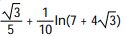
B)
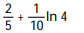
C)
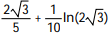
D)
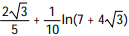

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the integral.
-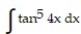
A)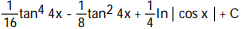
B)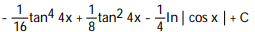
C)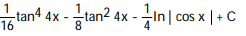
D)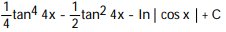
-
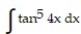
A)
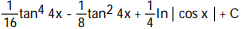
B)
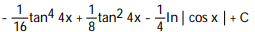
C)
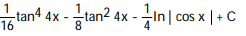
D)
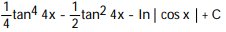

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the integral.
-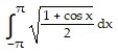
A) 4
B) 2
C) 1
D) 0
-
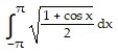
A) 4
B) 2
C) 1
D) 0

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the integral.
-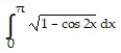
A) 2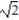
B)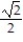
C) 2
D)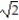
-
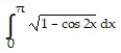
A) 2
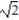
B)
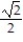
C) 2
D)
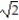

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the integral.
-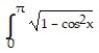 dx
dx
A)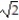
B)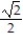
C) 0
D) 2
-
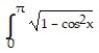 dx
dxA)
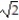
B)
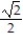
C) 0
D) 2

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate the integral.
-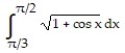
A) 2
B) 1
C) 2 +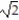
D) 2 -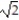
-
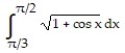
A) 2
B) 1
C) 2 +
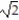
D) 2 -

Unlock Deck
Unlock for access to all 287 flashcards in this deck.
Unlock Deck
k this deck


