Deck 16: Multiple Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/299
Play
Full screen (f)
Deck 16: Multiple Integration
1
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-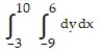
A) 33
B) 1
C) 87
D) 195
-
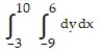
A) 33
B) 1
C) 87
D) 195
195
2
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-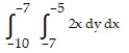
A) - 72
B) - 18
C) - 102
D) - 12
-
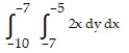
A) - 72
B) - 18
C) - 102
D) - 12
- 102
3
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-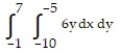
A) - 1800
B) - 600
C) - 960
D) 720
-
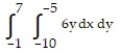
A) - 1800
B) - 600
C) - 960
D) 720
720
4
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-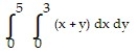
A) 4
B) 120
C) 60
D) 8
-
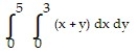
A) 4
B) 120
C) 60
D) 8

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
5
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-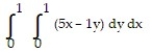
A) - 3
B) 2
C) 13
D) 3
-
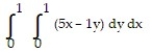
A) - 3
B) 2
C) 13
D) 3

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
6
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-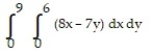
A) -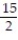
B) - 45
C) -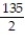
D) - 405
-
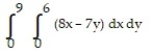
A) -
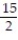
B) - 45
C) -
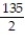
D) - 405

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
7
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-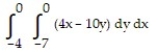
A) 27
B) 756
C) 108
D) 189
-
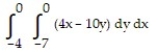
A) 27
B) 756
C) 108
D) 189

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
8
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-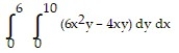
A) 300
B) 1800
C) 3000
D) 18000
-
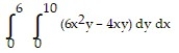
A) 300
B) 1800
C) 3000
D) 18000

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
9
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-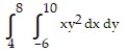
A) -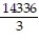
B)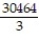
C)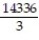
D) -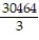
-
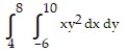
A) -
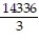
B)
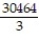
C)
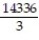
D) -
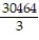

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
10
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-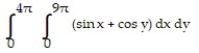
A) 8
B) 4
C) 9
D) 5
-
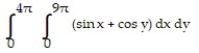
A) 8
B) 4
C) 9
D) 5

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
11
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-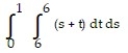
A)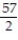
B)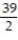
C) 24
D) 15
-
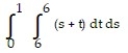
A)
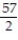
B)
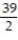
C) 24
D) 15

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the double integral over the given region.
-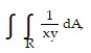 R = {(x, y): 9 x 10, 9 y 10}
R = {(x, y): 9 x 10, 9 y 10}
A)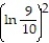
B)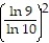
C)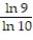
D) ln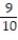
-
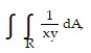 R = {(x, y): 9 x 10, 9 y 10}
R = {(x, y): 9 x 10, 9 y 10}A)
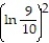
B)
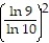
C)
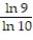
D) ln
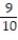

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the double integral over the given region.
-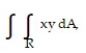 R = {(x, y): 9 x 10, 1 y 5}
R = {(x, y): 9 x 10, 1 y 5}
A) 114
B) 152
C) 228
D) 76
-
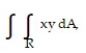 R = {(x, y): 9 x 10, 1 y 5}
R = {(x, y): 9 x 10, 1 y 5} A) 114
B) 152
C) 228
D) 76

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
14
Evaluate the double integral over the given region.
-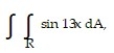 R =
R = 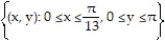
A)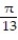
B)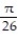
C)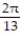
D)
-
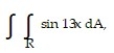 R =
R = 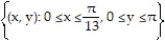
A)
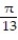
B)
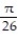
C)
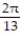
D)

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the double integral over the given region.
-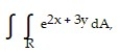 R = {(x, y): 0 x 1, 0 y 1}
R = {(x, y): 0 x 1, 0 y 1}
A)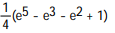
B)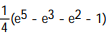
C)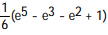
D)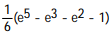
-
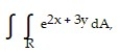 R = {(x, y): 0 x 1, 0 y 1}
R = {(x, y): 0 x 1, 0 y 1}A)
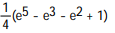
B)
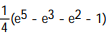
C)
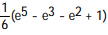
D)
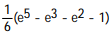

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the double integral over the given region.
-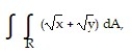 R = {(x, y): 0 x 1, 0 y 1}
R = {(x, y): 0 x 1, 0 y 1}
A)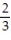
B)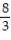
C)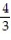
D)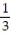
-
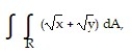 R = {(x, y): 0 x 1, 0 y 1}
R = {(x, y): 0 x 1, 0 y 1}A)
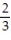
B)
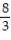
C)
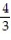
D)
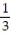

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the double integral over the given region.
-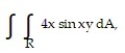 R = {(x, y): 0 x , 0 y 1}
R = {(x, y): 0 x , 0 y 1}
A) 4
B)
C)
D) 4 - 4
-
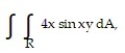 R = {(x, y): 0 x , 0 y 1}
R = {(x, y): 0 x , 0 y 1}A) 4
B)
C)

D) 4 - 4

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the double integral over the given region.
-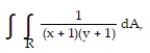 R = {(x, y): 0 x 6, 0 y 4}
R = {(x, y): 0 x 6, 0 y 4}
A) ln 7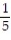
B) ln 7 ln 5
C) 5 ln 7
D) ln 35
-
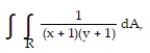 R = {(x, y): 0 x 6, 0 y 4}
R = {(x, y): 0 x 6, 0 y 4}A) ln 7
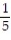
B) ln 7 ln 5
C) 5 ln 7
D) ln 35

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the double integral over the given region.
-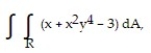 R = {(x, y): 0 x 1, 0 y 2}
R = {(x, y): 0 x 1, 0 y 2}
A)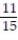
B)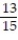
C) -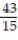
D)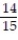
-
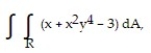 R = {(x, y): 0 x 1, 0 y 2}
R = {(x, y): 0 x 1, 0 y 2}A)
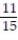
B)
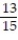
C) -
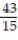
D)
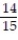

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
20
Find the average value of the function f over the given region.
-f(x, y) = 2x + 8y; R = {(x, y): 0 x 1, 0 y 1}
A) 10
B) 5
C) 6
D) 9
-f(x, y) = 2x + 8y; R = {(x, y): 0 x 1, 0 y 1}
A) 10
B) 5
C) 6
D) 9

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
21
Find the average value of the function f over the given region.
-f(x, y) = 10x + 3y; R = {(x, y): 0 x 2, 0 y 10}
A) 15
B) 25
C)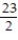
D) 10
-f(x, y) = 10x + 3y; R = {(x, y): 0 x 2, 0 y 10}
A) 15
B) 25
C)
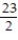
D) 10

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
22
Find the average value of the function f over the given region.
-f(x, y) = 5x + 10y over the triangle with vertices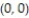 ,
, 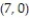 , and
, and 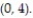
A)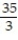
B) 15
C) 25
D) 13
-f(x, y) = 5x + 10y over the triangle with vertices
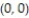 ,
, 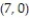 , and
, and 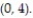
A)
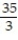
B) 15
C) 25
D) 13

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
23
Find the average value of the function f over the given region.
-f(x, y) = 10x + 7y over the region bounded by the coordinate axes and the lines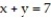 and
and 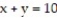 .
.
A) 73
B)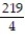
C)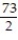
D)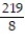
-f(x, y) = 10x + 7y over the region bounded by the coordinate axes and the lines
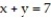 and
and 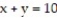 .
.A) 73
B)
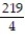
C)
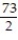
D)
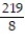

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
24
Find the average value of the function f over the given region.
-f(x, y) = sin 3(x + y); R =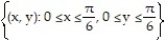
A)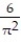
B) 4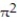
C)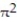
D)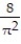
-f(x, y) = sin 3(x + y); R =
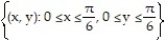
A)
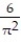
B) 4
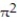
C)
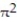
D)
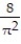

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
25
Find the average value of the function f over the given region.
-f(x, y) =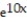 ; R =
; R = 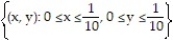
A)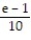
B)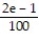
C) 2e - 1
D) e - 1
-f(x, y) =
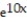 ; R =
; R = 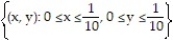
A)
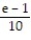
B)
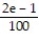
C) 2e - 1
D) e - 1

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
26
Find the average value of the function f over the given region.
-f(x, y) =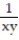 ; R = {(x, y): 1 x 3, 1 y 3}
; R = {(x, y): 1 x 3, 1 y 3}
A)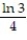
B)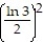
C)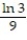
D)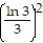
-f(x, y) =
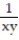 ; R = {(x, y): 1 x 3, 1 y 3}
; R = {(x, y): 1 x 3, 1 y 3}A)
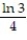
B)
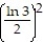
C)
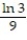
D)
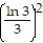

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
27
Find the average value of the function f over the given region.
-f(x, y) =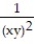 ; R = {(x, y): 1 x 5, 1 y 5}
; R = {(x, y): 1 x 5, 1 y 5}
A)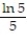
B)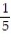
C)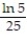
D)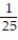
-f(x, y) =
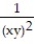 ; R = {(x, y): 1 x 5, 1 y 5}
; R = {(x, y): 1 x 5, 1 y 5}A)
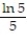
B)
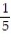
C)
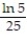
D)
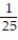

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
28
Find the average value of the function f over the given region.
-f(x, y) =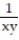 over the region bounded by
over the region bounded by 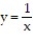 ,
, 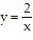 ,
, 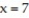 , and
, and 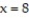 .
.
A) ln 2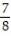
B) ln 2
C) ln 2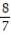
D) 56 ln 2
-f(x, y) =
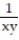 over the region bounded by
over the region bounded by 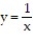 ,
, 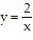 ,
, 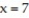 , and
, and 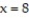 .
.A) ln 2
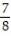
B) ln 2
C) ln 2
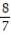
D) 56 ln 2

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
29
Find the average value of the function f over the given region.
-f(x, y) =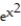 over the region bounded by
over the region bounded by 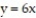 ,
, 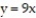 ,
, 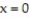 , and
, and 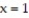 .
.
A) e - 1
B)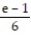
C) 2e - 1
D)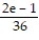
-f(x, y) =
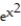 over the region bounded by
over the region bounded by 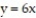 ,
, 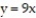 ,
, 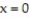 , and
, and 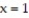 .
.A) e - 1
B)
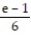
C) 2e - 1
D)
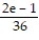

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
-The northern third of Indiana is a rectangle measuring 96 miles by 132 miles. Thus, let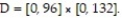 Assuming that the total annual snowfall (in inches), S(x,y), at
Assuming that the total annual snowfall (in inches), S(x,y), at 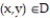 is given by the function S(x,y) = 60
is given by the function S(x,y) = 60 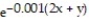 with (x,y)
with (x,y)  D, find the average snowfall on D.
D, find the average snowfall on D.
A)52.06 inches
B) 52.44 inches
C)51.78 inches
D) 51.14 inches
-The northern third of Indiana is a rectangle measuring 96 miles by 132 miles. Thus, let
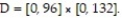 Assuming that the total annual snowfall (in inches), S(x,y), at
Assuming that the total annual snowfall (in inches), S(x,y), at 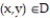 is given by the function S(x,y) = 60
is given by the function S(x,y) = 60 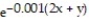 with (x,y)
with (x,y)  D, find the average snowfall on D.
D, find the average snowfall on D.A)52.06 inches
B) 52.44 inches
C)51.78 inches
D) 51.14 inches

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
-If f(x, y) = ( 3000 )/(1 +
)/(1 + 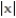 /2) represents the population density of a planar region on Earth, where x and y are measured in miles, find the number of people within the rectangle -7 x 7 and -3 y 0.
/2) represents the population density of a planar region on Earth, where x and y are measured in miles, find the number of people within the rectangle -7 x 7 and -3 y 0.
A)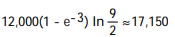
B)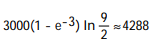
C)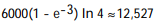
D)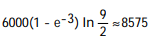
-If f(x, y) = ( 3000
 )/(1 +
)/(1 + 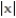 /2) represents the population density of a planar region on Earth, where x and y are measured in miles, find the number of people within the rectangle -7 x 7 and -3 y 0.
/2) represents the population density of a planar region on Earth, where x and y are measured in miles, find the number of people within the rectangle -7 x 7 and -3 y 0.A)
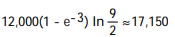
B)
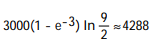
C)
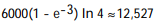
D)
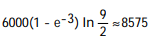

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
32
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = 6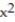 y; R = {(x, y): 0 x 4, 0 y 3}
y; R = {(x, y): 0 x 4, 0 y 3}
A) 576
B) 1256
C) 2256
D) 676
-z = 6
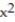 y; R = {(x, y): 0 x 4, 0 y 3}
y; R = {(x, y): 0 x 4, 0 y 3}A) 576
B) 1256
C) 2256
D) 676

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
33
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z =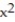 +
+ 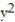 ; R = {(x, y): 0 x 1, 0 y 1}
; R = {(x, y): 0 x 1, 0 y 1}
A)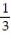
B)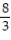
C)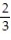
D)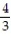
-z =
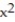 +
+ 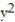 ; R = {(x, y): 0 x 1, 0 y 1}
; R = {(x, y): 0 x 1, 0 y 1}A)
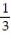
B)
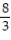
C)
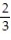
D)
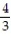

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
34
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = 8x + 4y + 7; R = {(x, y): 0 x 1, 1 y 3}
A) 28
B) 26
C) 36
D) 38
-z = 8x + 4y + 7; R = {(x, y): 0 x 1, 1 y 3}
A) 28
B) 26
C) 36
D) 38

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
35
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = 4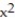 + 9
+ 9 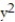 ; R = {(x, y): 0 x 1, 0 y 1}
; R = {(x, y): 0 x 1, 0 y 1}
A)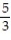
B)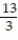
C)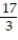
D)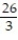
-z = 4
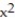 + 9
+ 9 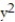 ; R = {(x, y): 0 x 1, 0 y 1}
; R = {(x, y): 0 x 1, 0 y 1}A)
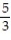
B)
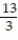
C)
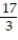
D)
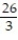

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
36
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = ; R = {(x, y): 0 x 1, 1 y e}
; R = {(x, y): 0 x 1, 1 y e}
A)
B)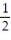
C)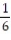
D)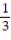
-z =
 ; R = {(x, y): 0 x 1, 1 y e}
; R = {(x, y): 0 x 1, 1 y e}A)

B)
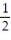
C)
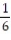
D)
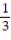

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
37
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The coordinate axes and the line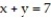
A)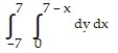
B)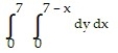
C)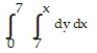
D)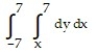
-The coordinate axes and the line
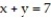
A)
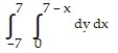
B)
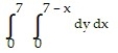
C)
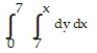
D)
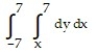

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
38
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The coordinate axes and the line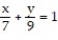
A)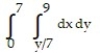
B)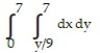
C)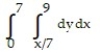
D)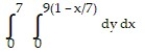
-The coordinate axes and the line
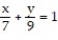
A)
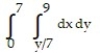
B)
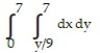
C)
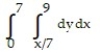
D)
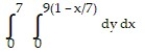

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
39
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The lines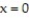 ,
, 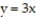 , and
, and 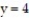
A)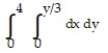
B)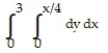
C)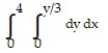
D)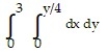
-The lines
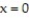 ,
, 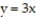 , and
, and 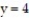
A)
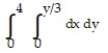
B)
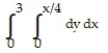
C)
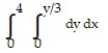
D)
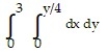

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
40
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The parabola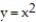 and the line
and the line 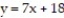
A)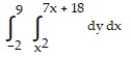
B)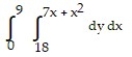
C)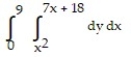
D)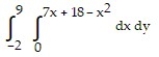
-The parabola
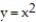 and the line
and the line 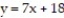
A)
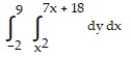
B)
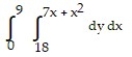
C)
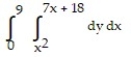
D)
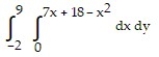

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
41
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The curve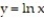 and the lines
and the lines 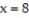 and
and 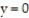
A)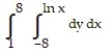
B)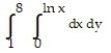
C)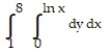
D)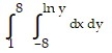
-The curve
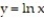 and the lines
and the lines 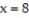 and
and 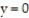
A)
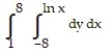
B)
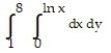
C)
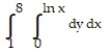
D)
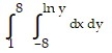

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
42
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The parabola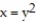 and the line
and the line 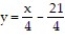
A)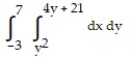
B)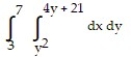
C)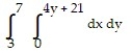
D)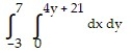
-The parabola
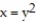 and the line
and the line 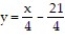
A)
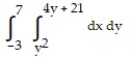
B)
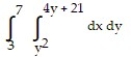
C)
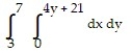
D)
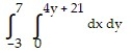

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
43
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The curve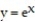 and the lines
and the lines 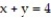 and
and 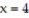
A)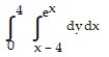
B)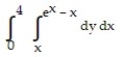
C)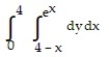
D)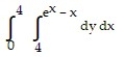
-The curve
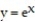 and the lines
and the lines 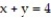 and
and 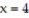
A)
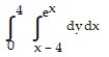
B)
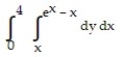
C)
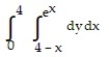
D)
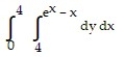

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
44
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The lines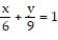 ,
, 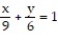 , and
, and 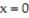
A)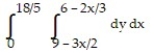
B)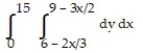
C)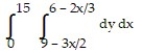
D)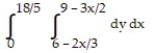
-The lines
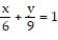 ,
, 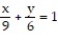 , and
, and 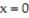
A)
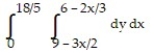
B)
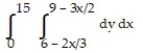
C)
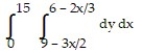
D)
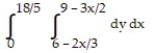

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
45
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The lines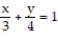 ,
, 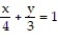 , and
, and 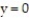
A)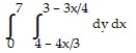
B)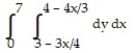
C)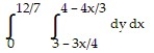
D)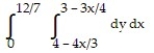
-The lines
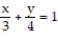 ,
, 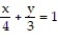 , and
, and 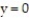
A)
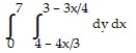
B)
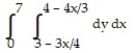
C)
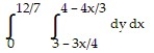
D)
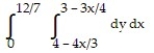

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
46
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The curves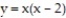 and
and 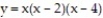
A)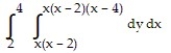
B)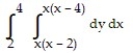
C)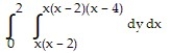
D)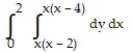
-The curves
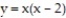 and
and 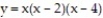
A)
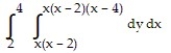
B)
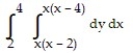
C)
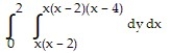
D)
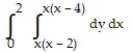

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the integral.
-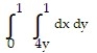
A) 3
B) -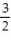
C)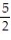
D) -1
-
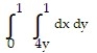
A) 3
B) -
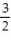
C)
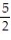
D) -1

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the integral.
-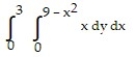
A) 27
B) 9
C)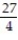
D)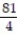
-
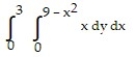
A) 27
B) 9
C)
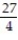
D)

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the integral.
-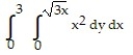
A)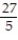
B)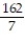
C)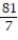
D)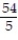
-
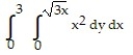
A)
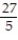
B)
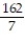
C)
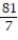
D)
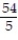

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
50
Evaluate the integral.
-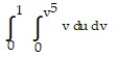
A)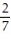
B)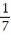
C)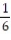
D)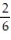
-
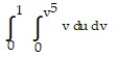
A)
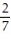
B)
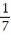
C)
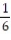
D)
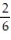

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the integral.
-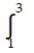
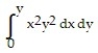
A)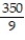
B)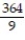
C)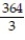
D)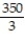
-
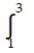
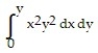
A)
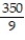
B)
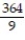
C)
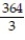
D)
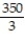

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the integral.
-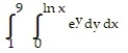
A) 16
B) 50
C) 32
D) 25
-
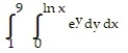
A) 16
B) 50
C) 32
D) 25

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the integral.
-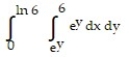
A)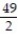
B)
C)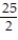
D)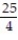
-
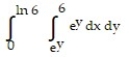
A)
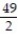
B)

C)
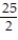
D)
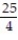

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the integral.
-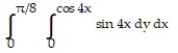
A)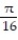
B)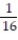
C)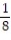
D)
-
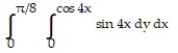
A)
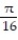
B)
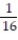
C)
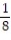
D)


Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate the integral.
-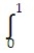
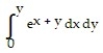
A)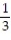 (e - 1) 2
(e - 1) 2
B)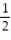 (e - 1) 2
(e - 1) 2
C)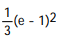
D)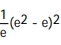
-
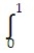
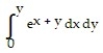
A)
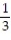 (e - 1) 2
(e - 1) 2 B)
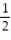 (e - 1) 2
(e - 1) 2 C)
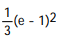
D)
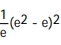

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
56
Integrate the function f over the given region.
-f(x, y) = xy over the triangular region with vertices (0, 0), ( 5, 0), and (0, 8)
A)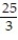
B)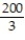
C)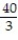
D)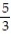
-f(x, y) = xy over the triangular region with vertices (0, 0), ( 5, 0), and (0, 8)
A)
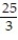
B)
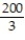
C)
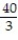
D)
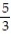

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
57
Integrate the function f over the given region.
-f(x, y) =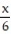 +
+ 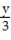 over the trapezoidal region bounded by the x-axis, y-axis, line
over the trapezoidal region bounded by the x-axis, y-axis, line 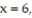 and line
and line 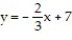
A)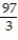
B)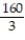
C)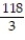
D)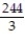
-f(x, y) =
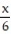 +
+ 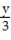 over the trapezoidal region bounded by the x-axis, y-axis, line
over the trapezoidal region bounded by the x-axis, y-axis, line 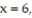 and line
and line 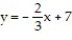
A)
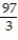
B)
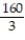
C)
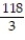
D)
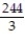

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
58
Integrate the function f over the given region.
-f(x, y) =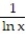 over the region bounded by the x-axis, line
over the region bounded by the x-axis, line 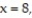 and curve
and curve 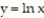
A) 7
B) 1
C) 8
D) 9
-f(x, y) =
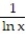 over the region bounded by the x-axis, line
over the region bounded by the x-axis, line 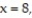 and curve
and curve 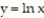
A) 7
B) 1
C) 8
D) 9

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
59
Integrate the function f over the given region.
-f(x, y) =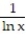 over the region bounded by the x-axis, line
over the region bounded by the x-axis, line 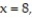 and curve
and curve 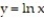
A) 8
B) 1
C) 7
D) 9
-f(x, y) =
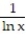 over the region bounded by the x-axis, line
over the region bounded by the x-axis, line 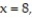 and curve
and curve 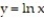
A) 8
B) 1
C) 7
D) 9

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
60
Find the volume of the indicated region.
-the region that lies under the paraboloid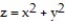 and above the triangle enclosed by the lines
and above the triangle enclosed by the lines 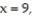
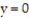 , and
, and 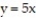
A)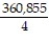
B) 8505
C) 76,545
D) 945
-the region that lies under the paraboloid
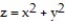 and above the triangle enclosed by the lines
and above the triangle enclosed by the lines 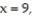
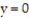 , and
, and 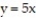
A)
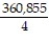
B) 8505
C) 76,545
D) 945

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
61
Find the volume of the indicated region.
-the tetrahedron bounded by the coordinate planes and the plane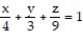
A) 18
B) 27
C) 54
D) 36
-the tetrahedron bounded by the coordinate planes and the plane
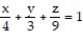
A) 18
B) 27
C) 54
D) 36

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
62
Find the volume of the indicated region.
-the region that lies under the plane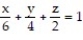 and above the square
and above the square 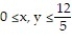
A)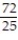
B)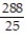
C)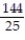
D)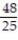
-the region that lies under the plane
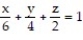 and above the square
and above the square 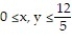
A)
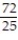
B)
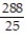
C)
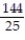
D)
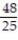

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
63
Find the volume of the indicated region.
-the solid cut from the first octant by the surface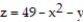
A)
B)
C)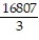
D)
-the solid cut from the first octant by the surface
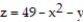
A)

B)

C)
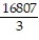
D)


Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
64
Find the volume of the indicated region.
-the region under the surface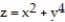 , and bounded by the planes
, and bounded by the planes 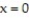 and
and 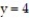 and the cylinder
and the cylinder 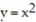
A)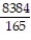
B)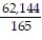
C)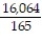
D)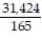
-the region under the surface
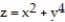 , and bounded by the planes
, and bounded by the planes 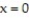 and
and 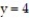 and the cylinder
and the cylinder 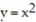
A)
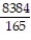
B)
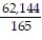
C)
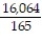
D)
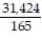

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
65
Find the volume of the indicated region.
-the region bounded by the paraboloid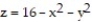 and the xy-plane
and the xy-plane
A) 64
B) 128
C)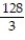
D)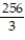
-the region bounded by the paraboloid
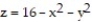 and the xy-plane
and the xy-planeA) 64
B) 128
C)
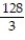
D)
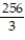

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
66
Find the volume of the indicated region.
-the region bounded by the paraboloid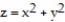 and the plane
and the plane 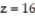
A)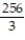
B) 64
C) 128
D)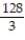
-the region bounded by the paraboloid
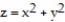 and the plane
and the plane 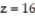
A)
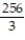
B) 64
C) 128
D)
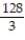

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
67
Find the volume of the indicated region.
-the region bounded by the paraboloid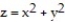 , the cylinder
, the cylinder 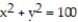 , and the
, and the 
A)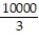
B) 5000
C)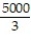
D) 2500
-the region bounded by the paraboloid
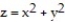 , the cylinder
, the cylinder 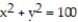 , and the
, and the 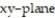
A)
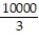
B) 5000
C)
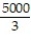
D) 2500

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
68
Find the volume of the indicated region.
-the region that lies under the plane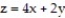 and over the triangle with vertices at
and over the triangle with vertices at 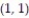 ,
, 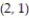 , and
, and 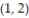
A) 8
B)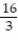
C) 4
D)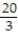
-the region that lies under the plane
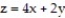 and over the triangle with vertices at
and over the triangle with vertices at 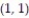 ,
, 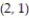 , and
, and 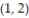
A) 8
B)
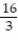
C) 4
D)
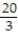

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
69
Find the volume of the indicated region.
-the region that lies under the plane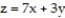 and over the triangle bounded by the lines
and over the triangle bounded by the lines 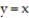 ,
, 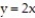 , and
, and 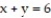
A) 50
B) 64
C) 56
D) 70
-the region that lies under the plane
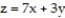 and over the triangle bounded by the lines
and over the triangle bounded by the lines 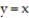 ,
, 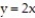 , and
, and 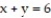
A) 50
B) 64
C) 56
D) 70

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
70
Write an equivalent double integral with the order of integration reversed.
-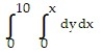
A)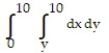
B)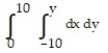
C)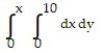
D)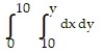
-
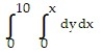
A)
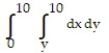
B)
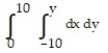
C)
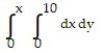
D)
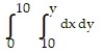

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
71
Write an equivalent double integral with the order of integration reversed.
-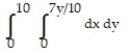
A)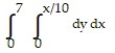
B)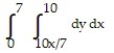
C)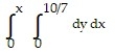
D)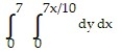
-
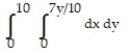
A)
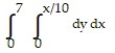
B)
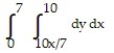
C)
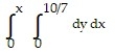
D)
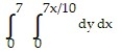

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
72
Write an equivalent double integral with the order of integration reversed.
-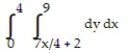
A)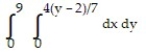
B)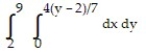
C)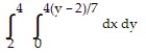
D)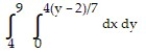
-
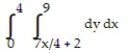
A)
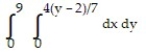
B)
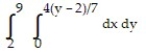
C)
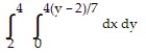
D)
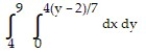

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
73
Write an equivalent double integral with the order of integration reversed.
-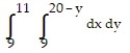
A)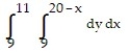
B)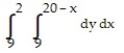
C)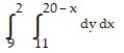
D)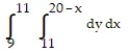
-
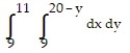
A)
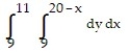
B)
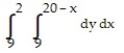
C)
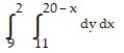
D)
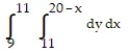

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
74
Write an equivalent double integral with the order of integration reversed.
-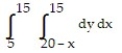
A)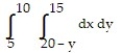
B)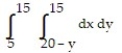
C)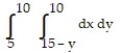
D)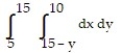
-
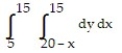
A)
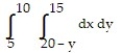
B)
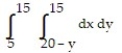
C)
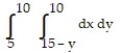
D)
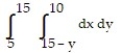

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
75
Write an equivalent double integral with the order of integration reversed.
-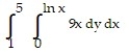
A)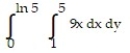
B)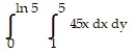
C)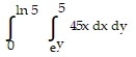
D)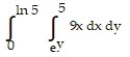
-
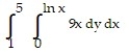
A)
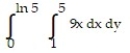
B)
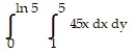
C)
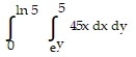
D)
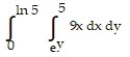

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
76
Write an equivalent double integral with the order of integration reversed.
-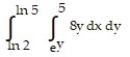
A)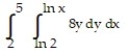
B)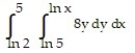
C)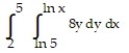
D)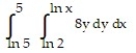
-
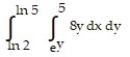
A)
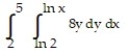
B)
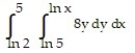
C)
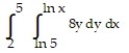
D)
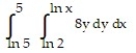

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
77
Write an equivalent double integral with the order of integration reversed.
-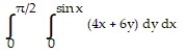
A)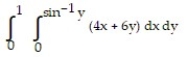
B)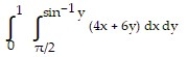
C)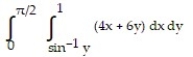
D)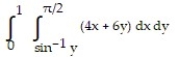
-
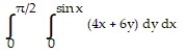
A)
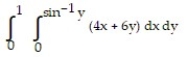
B)
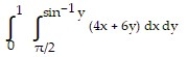
C)
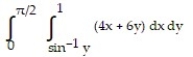
D)
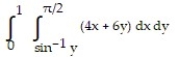

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
78
Write an equivalent double integral with the order of integration reversed.
-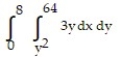
A)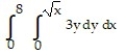
B)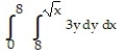
C)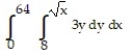
D)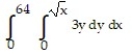
-
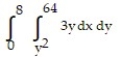
A)
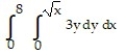
B)
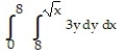
C)
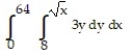
D)
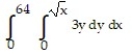

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
79
Write an equivalent double integral with the order of integration reversed.
-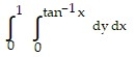
A)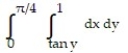
B)
C)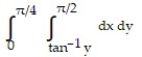
D)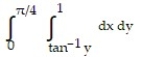
-
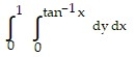
A)
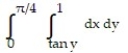
B)

C)
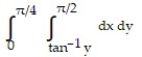
D)
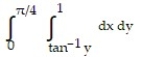

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck
80
Reverse the order of integration and then evaluate the integral.
-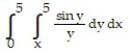
A) 1 - cos 5
B) - cos 5
C) cos 5
D) 1 + cos 5
-
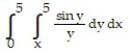
A) 1 - cos 5
B) - cos 5
C) cos 5
D) 1 + cos 5

Unlock Deck
Unlock for access to all 299 flashcards in this deck.
Unlock Deck
k this deck


