Deck 10: Sequences and Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/173
Play
Full screen (f)
Deck 10: Sequences and Infinite Series
1
Write the first four elements of the sequence.
-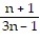
A)
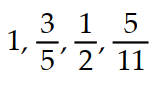
B)
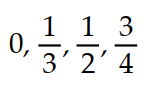
C)
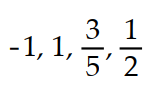
D)
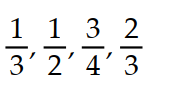
-
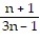
A)
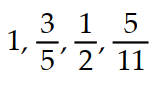
B)
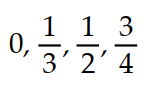
C)
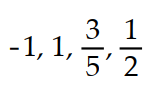
D)
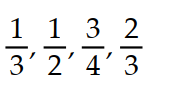
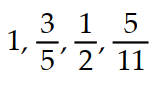
2
Write the first four elements of the sequence.
-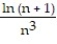
A)
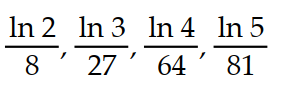
B)
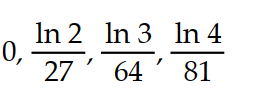
C)
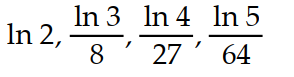
D)
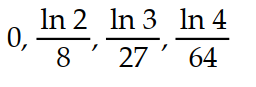
-
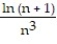
A)
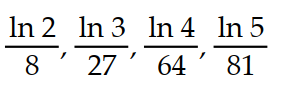
B)
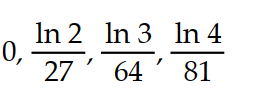
C)
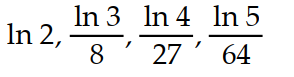
D)
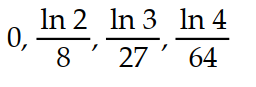
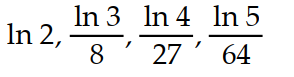
3
Write the first four elements of the sequence.
-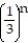
A)
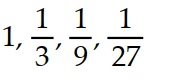
B)
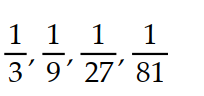
C)
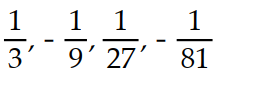
D)
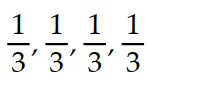
-
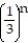
A)
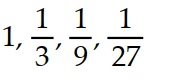
B)
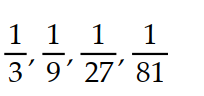
C)
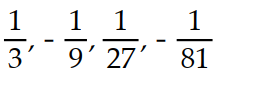
D)
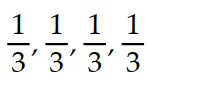
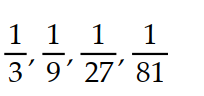
4
Write the first four elements of the sequence.
-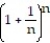
A)
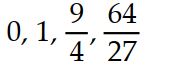
B)
C)
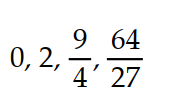
D)
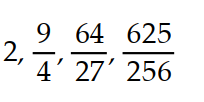
-
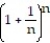
A)
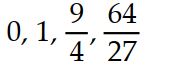
B)
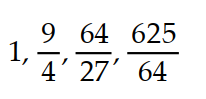
C)
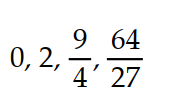
D)
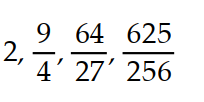

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
5
Write the first four elements of the sequence.
-sin (n )
A) 1, 0, -1, 0
B) 0, 1, 0, -1
C) 1, 1, 1, 1
D) 0, 0, 0, 0
-sin (n )
A) 1, 0, -1, 0
B) 0, 1, 0, -1
C) 1, 1, 1, 1
D) 0, 0, 0, 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
6
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
- = 1,
= 1, 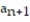 = 2
= 2 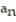
A) 2, 3, 4, 5, 6
B) 1, 2, 4, 8, 16
C) 2, 4, 8, 16, 32
D) 1, 3, 5, 7, 9
-
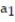 = 1,
= 1, 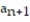 = 2
= 2 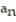
A) 2, 3, 4, 5, 6
B) 1, 2, 4, 8, 16
C) 2, 4, 8, 16, 32
D) 1, 3, 5, 7, 9

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
7
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-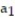 = 1,
= 1, 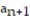 =
= 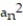
A) 1, 1, 1, 1, 1
B) 1, 2, 4, 8, 16, 32
C) 1, 3, 5, 7, 9
D) 1, 2, 4, 8, 16
-
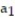 = 1,
= 1, 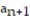 =
= 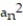
A) 1, 1, 1, 1, 1
B) 1, 2, 4, 8, 16, 32
C) 1, 3, 5, 7, 9
D) 1, 2, 4, 8, 16

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
8
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-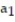 = 1,
= 1, 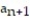 =
= 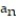 + 5
+ 5
A) 1, 6, 11, 16, 21, 26
B) 1, 6, 11, 16, 21
C) 6, 11, 16, 21, 26
D) 1, 5, 25, 125, 625, 3125
-
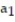 = 1,
= 1, 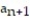 =
= 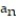 + 5
+ 5A) 1, 6, 11, 16, 21, 26
B) 1, 6, 11, 16, 21
C) 6, 11, 16, 21, 26
D) 1, 5, 25, 125, 625, 3125

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
9
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-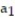 = 4,
= 4, 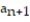 = -
= - 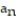
A) 4, -16, 64, -256, 1024
B) 4, 0, -4, -8, -12
C) 4, -4, 4, -4, 4
D) -4, 4, -4, 4, -4
-
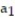 = 4,
= 4, 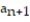 = -
= - 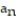
A) 4, -16, 64, -256, 1024
B) 4, 0, -4, -8, -12
C) 4, -4, 4, -4, 4
D) -4, 4, -4, 4, -4

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
10
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-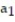 = 6,
= 6, 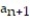 =
= 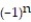
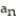
A) -6, 6, -6, 6, -6
B) 6, -6, 6, -6, 6
C) 6, -6, -6, 6, 6
D) 6, 6, -6, -6, 6
-
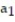 = 6,
= 6, 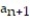 =
= 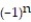
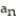
A) -6, 6, -6, 6, -6
B) 6, -6, 6, -6, 6
C) 6, -6, -6, 6, 6
D) 6, 6, -6, -6, 6

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
11
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-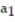 = 3,
= 3, 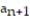 =
= 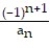
A)
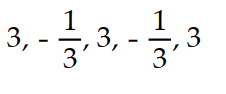
B)
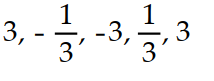
C)
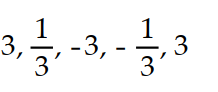
D)
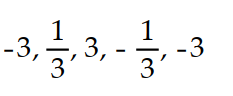
-
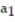 = 3,
= 3, 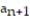 =
= 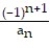
A)
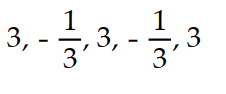
B)
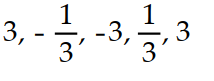
C)
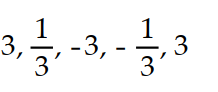
D)
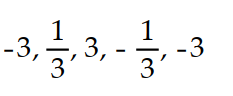

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
12
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-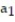 = 1,
= 1, 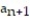 =
= 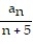
A)
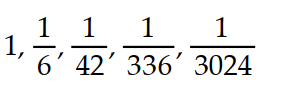
B)
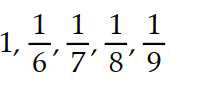
C)
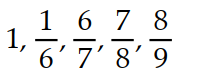
D)
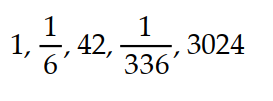
-
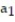 = 1,
= 1, 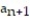 =
= 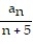
A)
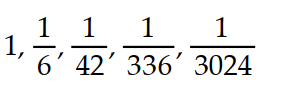
B)
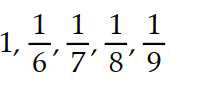
C)
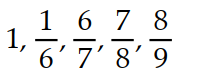
D)
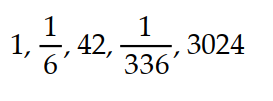

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
13
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
- = 1,
= 1, 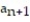 =
= 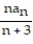
A)
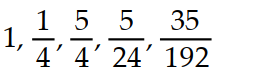
B)
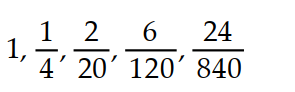
C)
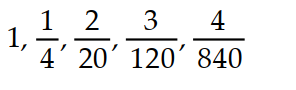
D)
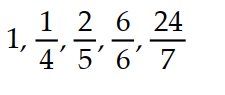
-
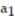 = 1,
= 1, 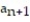 =
= 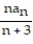
A)
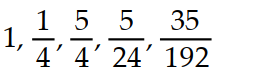
B)
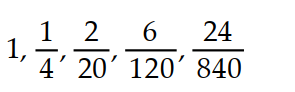
C)
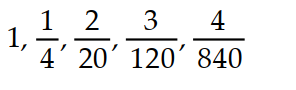
D)
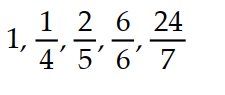

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
14
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-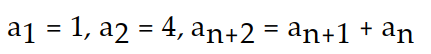
A) 1, 4, 5, 10, 15
B) 1, 4, 5, 9, 14
C) 1, 1, 2, 3, 5
D) 1, 4, 5, 6, 7
-
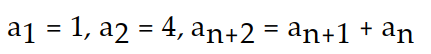
A) 1, 4, 5, 10, 15
B) 1, 4, 5, 9, 14
C) 1, 1, 2, 3, 5
D) 1, 4, 5, 6, 7

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
15
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-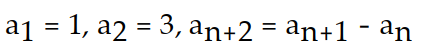
A) 1, 3, 2, -1, -3
B) 1, -3, 4, -5, 6
C) 1, 3, 2, 1, 0
D) 1, -1, 2, -3, 5
-
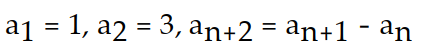
A) 1, 3, 2, -1, -3
B) 1, -3, 4, -5, 6
C) 1, 3, 2, 1, 0
D) 1, -1, 2, -3, 5

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
16
Find a formula for the nth term of the sequence.
-7, 8, 9, 10, 11 (integers beginning with 7)
A)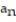 = n + 6
= n + 6
B)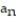 = n + 7
= n + 7
C)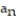 = n - 7
= n - 7
D)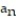 = n + 8
= n + 8
-7, 8, 9, 10, 11 (integers beginning with 7)
A)
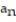 = n + 6
= n + 6B)
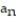 = n + 7
= n + 7C)
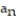 = n - 7
= n - 7D)
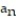 = n + 8
= n + 8
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
17
Find a formula for the nth term of the sequence.
--5, -4, -3, -2, -1 (integers beginning with -5)
A)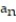 = n - 6
= n - 6
B)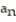 = n - 5
= n - 5
C)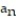 = n + 5
= n + 5
D)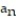 = n - 4
= n - 4
--5, -4, -3, -2, -1 (integers beginning with -5)
A)
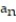 = n - 6
= n - 6B)
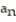 = n - 5
= n - 5C)
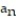 = n + 5
= n + 5D)
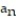 = n - 4
= n - 4
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
18
Find a formula for the nth term of the sequence.
-6, -6, 6, -6, 6 ( 6's with alternating signs)
A)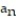 = 6
= 6 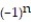
B)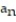 = 6
= 6 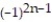
C)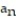 = 6
= 6 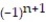
D)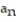 = 6
= 6 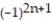
-6, -6, 6, -6, 6 ( 6's with alternating signs)
A)
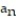 = 6
= 6 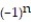
B)
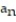 = 6
= 6 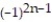
C)
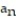 = 6
= 6 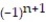
D)
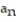 = 6
= 6 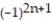

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
19
Find a formula for the nth term of the sequence.
-1, - ,
, 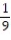 , -
, - 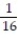 ,
, 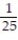 (reciprocals of squares with alternating signs)
(reciprocals of squares with alternating signs)
A)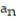 =
= 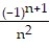
B)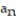 =
= 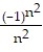
C)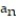 =
= 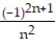
D)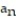 =
= 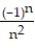
-1, -
 ,
, 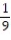 , -
, - 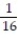 ,
, 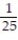 (reciprocals of squares with alternating signs)
(reciprocals of squares with alternating signs)A)
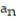 =
= 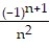
B)
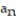 =
= 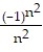
C)
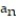 =
= 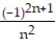
D)
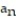 =
= 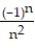

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
20
Find a formula for the nth term of the sequence.
-6, 8, 10, 12, 14 (every other integer starting with 6)
A)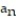 = 2n + 5
= 2n + 5
B)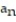 = 2n + 4
= 2n + 4
C)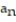 = n + 11
= n + 11
D)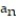 = n + 10
= n + 10
-6, 8, 10, 12, 14 (every other integer starting with 6)
A)
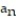 = 2n + 5
= 2n + 5B)
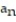 = 2n + 4
= 2n + 4C)
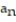 = n + 11
= n + 11D)
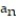 = n + 10
= n + 10
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
21
Find a formula for the nth term of the sequence.
-0, 2, 0, 2, 0 (alternating 0's and 2's)
A)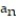 = 1 +
= 1 + 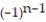
B)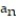 = 1 +
= 1 + 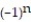
C)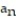 = 1 +
= 1 + 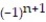
D)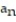 = 1 -
= 1 - 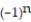
-0, 2, 0, 2, 0 (alternating 0's and 2's)
A)
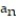 = 1 +
= 1 + 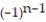
B)
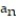 = 1 +
= 1 + 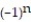
C)
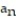 = 1 +
= 1 + 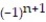
D)
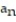 = 1 -
= 1 - 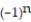

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
22
Find a formula for the nth term of the sequence.
-0,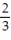 , 0,
, 0, 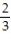 , 0 (alternating 0's and
, 0 (alternating 0's and 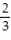 's)
's)
A)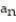 =
= 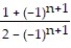
B)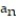 =
= 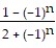
C)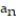 =
= 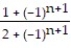
D)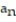 =
= 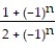
-0,
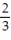 , 0,
, 0, 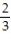 , 0 (alternating 0's and
, 0 (alternating 0's and 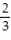 's)
's)A)
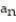 =
= 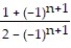
B)
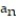 =
= 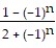
C)
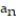 =
= 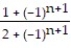
D)
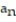 =
= 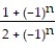

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
23
Find a formula for the nth term of the sequence.
-0, 0, 2, 2, 0, 0, 2, 2 (alternating 0's and 2's in pairs)
A)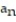 = 1 -
= 1 - 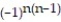
B)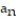 =
= 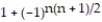
C)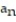 = 1 +
= 1 + 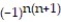
D)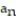 = 1 +
= 1 + 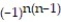
-0, 0, 2, 2, 0, 0, 2, 2 (alternating 0's and 2's in pairs)
A)
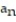 = 1 -
= 1 - 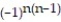
B)
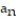 =
= 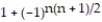
C)
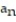 = 1 +
= 1 + 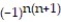
D)
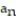 = 1 +
= 1 + 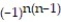

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
24
Find a formula for the nth term of the sequence.
-0, 2, 2, 2, 0, 2, 2, 2 (0, 2, 2, 2 repeated)
A)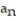 = 1 +
= 1 + 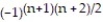
B)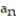 = 1 +
= 1 + 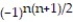
C)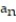 = 1 +
= 1 + 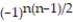
D)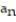 = 1 +
= 1 + 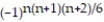
-0, 2, 2, 2, 0, 2, 2, 2 (0, 2, 2, 2 repeated)
A)
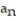 = 1 +
= 1 + 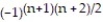
B)
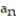 = 1 +
= 1 + 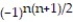
C)
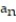 = 1 +
= 1 + 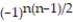
D)
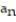 = 1 +
= 1 + 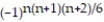

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
25
Find a formula for the nth term of the sequence.
-0, -1, 0, 1, 0, -1, 0, 1 (0, -1, 0, 1 repeated)
A)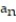 = sin
= sin 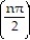
B)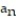 = sin(n )
= sin(n )
C)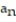 = cos(n )
= cos(n )
D)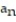 = cos
= cos 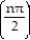
-0, -1, 0, 1, 0, -1, 0, 1 (0, -1, 0, 1 repeated)
A)
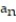 = sin
= sin 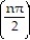
B)
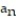 = sin(n )
= sin(n )C)
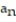 = cos(n )
= cos(n )D)
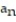 = cos
= cos 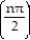

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
26
Find the limit of the sequence if it converges; otherwise indicate divergence.
-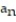 = 4 +
= 4 + 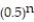
A) 4.5
B) 4
C) 5
D) Diverges
-
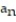 = 4 +
= 4 + 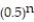
A) 4.5
B) 4
C) 5
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
27
Find the limit of the sequence if it converges; otherwise indicate divergence.
-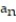 =
= 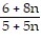
A) -10
B)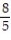
C)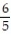
D) Diverges
-
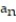 =
= 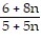
A) -10
B)
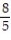
C)
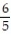
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
28
Find the limit of the sequence if it converges; otherwise indicate divergence.
-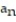 =
= 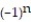

A) 3
B) ±3
C) 0
D) Diverges
-
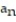 =
= 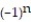

A) 3
B) ±3
C) 0
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
29
Find the limit of the sequence if it converges; otherwise indicate divergence.
-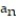 =
= 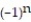
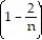
A) 2
B) 0
C) 1
D) Diverges
-
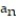 =
= 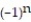
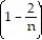
A) 2
B) 0
C) 1
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
30
Find the limit of the sequence if it converges; otherwise indicate divergence.
-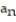 =
= 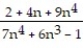
A) -9
B)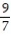
C)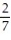
D) Diverges
-
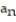 =
= 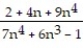
A) -9
B)
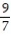
C)
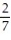
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
31
Find the limit of the sequence if it converges; otherwise indicate divergence.
-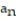 =
= 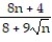
A)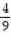
B)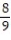
C) 1
D) Diverges
-
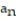 =
= 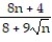
A)
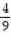
B)
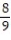
C) 1
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
32
Find the limit of the sequence if it converges; otherwise indicate divergence.
-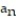 =
= 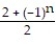
A)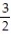
B) 1
C) 0
D) Diverges
-
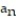 =
= 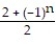
A)
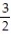
B) 1
C) 0
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
33
Find the limit of the sequence if it converges; otherwise indicate divergence.
-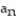 = 1 +
= 1 + 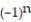 +
+ 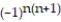
A) 1
B) 3
C) 0
D) Diverges
-
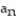 = 1 +
= 1 + 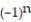 +
+ 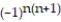
A) 1
B) 3
C) 0
D) Diverges

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
34
Assume that the sequence converges and find its limit.
-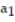 = 5,
= 5, 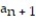 =
= 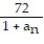
A) 6
B) 8
C) 4
D) 5
-
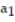 = 5,
= 5, 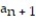 =
= 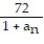
A) 6
B) 8
C) 4
D) 5

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
35
Assume that the sequence converges and find its limit.
-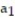 = -2,
= -2, 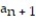 =
= 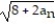
A) -6
B) 8
C) -2
D) 4
-
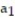 = -2,
= -2, 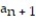 =
= 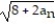
A) -6
B) 8
C) -2
D) 4

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
36
Assume that the sequence converges and find its limit.
-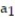 = 4,
= 4, 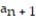 =
= 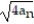
A) -4
B) 4
C) 1
D) 16
-
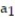 = 4,
= 4, 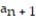 =
= 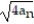
A) -4
B) 4
C) 1
D) 16

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
37
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-3 + +
+ 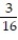 + ... +
+ ... + 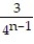 + ...
+ ...
A)
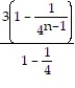 ; 4
; 4
B)
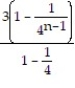 ;
; 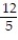
C)
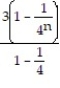 ;
; 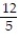
D)
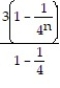 ; 4
; 4
-3 +
 +
+ 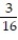 + ... +
+ ... + 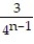 + ...
+ ...A)
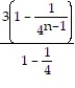 ; 4
; 4B)
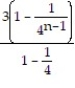 ;
; 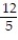
C)
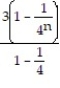 ;
; 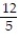
D)
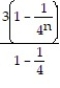 ; 4
; 4
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
38
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-7 + 63 + 567 + ... + 7 .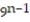 + ...
+ ...
A)
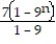 ;
; 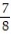
B)
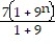 ;
; 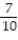
C)
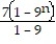 ; series diverges
; series diverges
D)
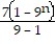 ; series diverges
; series diverges
-7 + 63 + 567 + ... + 7 .
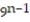 + ...
+ ...A)
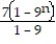 ;
; 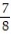
B)
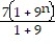 ;
; 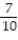
C)
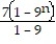 ; series diverges
; series divergesD)
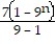 ; series diverges
; series diverges
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
39
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-3 - +
+ 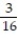 -
- 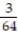 + ... +
+ ... + 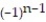
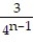 + ...
+ ...
A)
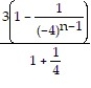 ; 4
; 4
B)
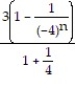 ; 4
; 4
C)
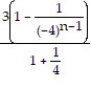 ;
; 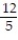
D)
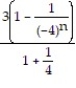 ;
; 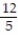
-3 -
 +
+ 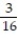 -
- 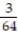 + ... +
+ ... + 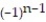
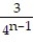 + ...
+ ...A)
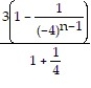 ; 4
; 4B)
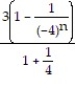 ; 4
; 4C)
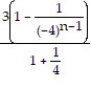 ;
; 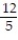
D)
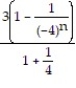 ;
; 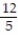

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
40
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-3 - 21 + 147 - 1029 + ... +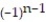 3 .
3 .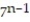 + ...
+ ...
A)
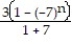 ;
; 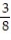
B)
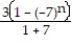 ; series diverges
; series diverges
C)
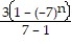 ; series diverges
; series diverges
D)
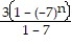 ;
; 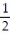
-3 - 21 + 147 - 1029 + ... +
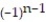 3 .
3 .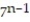 + ...
+ ...A)
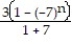 ;
; 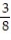
B)
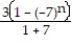 ; series diverges
; series divergesC)
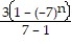 ; series diverges
; series divergesD)
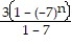 ;
; 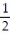

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
41
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-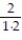 +
+ 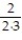 +
+ 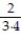 + ... +
+ ... + 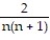 + ...
+ ...
A)
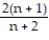 ; 2
; 2
B)
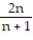 ; 2
; 2
C)
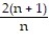 ; 2
; 2
D)
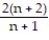 ; 2
; 2
-
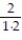 +
+ 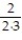 +
+ 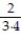 + ... +
+ ... + 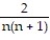 + ...
+ ...A)
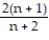 ; 2
; 2B)
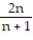 ; 2
; 2C)
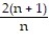 ; 2
; 2D)
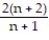 ; 2
; 2
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
42
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-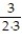 +
+ 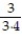 +
+ 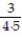 + ... +
+ ... + 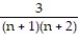 + ...
+ ...
A)
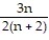 ;
; 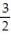
B)
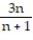 ; 3
; 3
C)
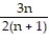 ;
; 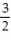
D)
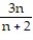 ; 3
; 3
-
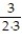 +
+ 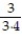 +
+ 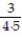 + ... +
+ ... + 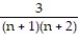 + ...
+ ...A)
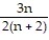 ;
; 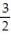
B)
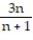 ; 3
; 3C)
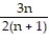 ;
; 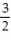
D)
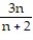 ; 3
; 3
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
43
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-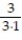 +
+ 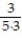 +
+ 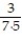 + ... +
+ ... + 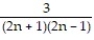 + ...
+ ...
A)
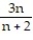 ; 3
; 3
B)
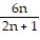 ; 3
; 3
C)
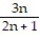 ;
; 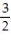
D)
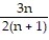 ;
; 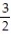
-
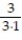 +
+ 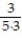 +
+ 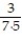 + ... +
+ ... + 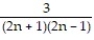 + ...
+ ...A)
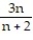 ; 3
; 3B)
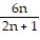 ; 3
; 3C)
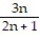 ;
; 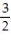
D)
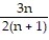 ;
; 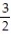

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
44
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-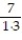 +
+ 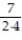 +
+ 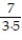 + ... +
+ ... + 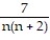 + ...
+ ...
A)
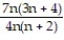 ;
; 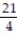
B)
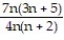 ;
; 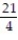
C)
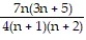 ;
; 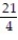
D)
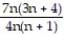 ;
; 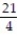
-
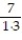 +
+ 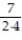 +
+ 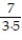 + ... +
+ ... + 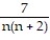 + ...
+ ...A)
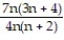 ;
; 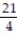
B)
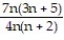 ;
; 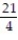
C)
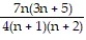 ;
; 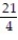
D)
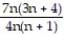 ;
; 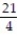

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
45
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-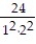 +
+ 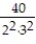 +
+ 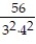 + ... +
+ ... + 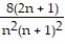 + ...
+ ...
A)
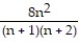 ; 8
; 8
B)
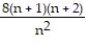 ; 8
; 8
C)
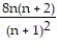 ; 8
; 8
D)
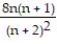 ; 8
; 8
-
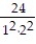 +
+ 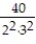 +
+ 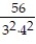 + ... +
+ ... + 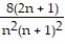 + ...
+ ...A)
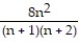 ; 8
; 8B)
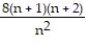 ; 8
; 8C)
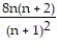 ; 8
; 8D)
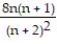 ; 8
; 8
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
46
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-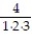 +
+ 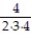 +
+ 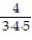 + ... +
+ ... + 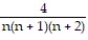 + ...
+ ...
A)
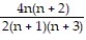 ; 2
; 2
B)
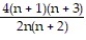 ; 2
; 2
C)
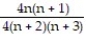 ; 1
; 1
D)
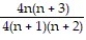 ; 1
; 1
-
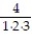 +
+ 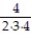 +
+ 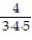 + ... +
+ ... + 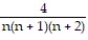 + ...
+ ...A)
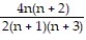 ; 2
; 2B)
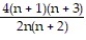 ; 2
; 2C)
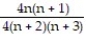 ; 1
; 1D)
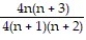 ; 1
; 1
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
-A company's annual revenue for the period since 2000 can be modeled by the function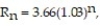 where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.
where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.
A) 2011
B) 2009
C) 2013
D) 2010
-A company's annual revenue for the period since 2000 can be modeled by the function
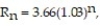 where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.
where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.A) 2011
B) 2009
C) 2013
D) 2010

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
-At a plant that packages bottled spring water, the water is passed through a sequence of ion-exchange filters to reduce the sodium content prior to bottling. Each filter removes 70% of the sodium present in the water passing through it. Determine the number of filters that must be used to reduce the sodium concentration from 30 parts-per-million to 7.20 parts-per-million.
A) 4 filters
B) 6 filters
C) 7 filters
D) 5 filters
-At a plant that packages bottled spring water, the water is passed through a sequence of ion-exchange filters to reduce the sodium content prior to bottling. Each filter removes 70% of the sodium present in the water passing through it. Determine the number of filters that must be used to reduce the sodium concentration from 30 parts-per-million to 7.20 parts-per-million.
A) 4 filters
B) 6 filters
C) 7 filters
D) 5 filters

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
49
Find the limit of the sequence or determine that the limit does not exist.
-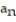 = ln( 9n + 9) - ln( 2n - 7)
= ln( 9n + 9) - ln( 2n - 7)
A) does not exist
B) ln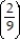
C) ln 7
D) ln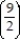
-
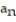 = ln( 9n + 9) - ln( 2n - 7)
= ln( 9n + 9) - ln( 2n - 7)A) does not exist
B) ln
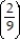
C) ln 7
D) ln
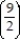

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
50
Find the limit of the sequence or determine that the limit does not exist.
-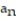 =
= 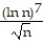
A) ln 7
B) does not exist
C)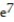
D) 0
-
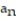 =
= 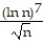
A) ln 7
B) does not exist
C)
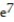
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
51
Find the limit of the sequence or determine that the limit does not exist.
-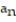 =
= 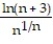
A) does not exist
B) ln 3
C) 0
D) 1
-
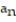 =
= 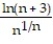
A) does not exist
B) ln 3
C) 0
D) 1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
52
Find the limit of the sequence or determine that the limit does not exist.
-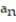 =
= 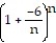
A) 1
B) does not exist
C) e
D)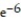
-
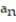 =
= 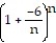
A) 1
B) does not exist
C) e
D)
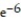

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
53
Find the limit of the sequence or determine that the limit does not exist.
-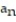 =
= 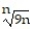
A) ln 9
B) 0
C) does not exist
D) 1
-
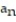 =
= 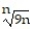
A) ln 9
B) 0
C) does not exist
D) 1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
54
Find the limit of the sequence or determine that the limit does not exist.
-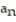 =
= 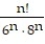
A)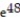
B) 0
C) 1
D) does not exist
-
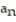 =
= 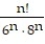
A)
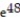
B) 0
C) 1
D) does not exist

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
55
Find the limit of the sequence or determine that the limit does not exist.
-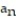 =
= 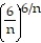
A) 1
B) ln 6
C) 0
D) does not exist
-
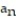 =
= 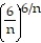
A) 1
B) ln 6
C) 0
D) does not exist

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
56
Find the limit of the sequence or determine that the limit does not exist.
-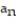 =
= 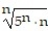
A) 0
B) does not exist
C) 1
D) 5
-
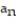 =
= 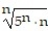
A) 0
B) does not exist
C) 1
D) 5

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
57
Find the limit of the sequence or determine that the limit does not exist.
-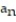 =
= 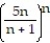
A) 0
B) 5
C) does not exist
D)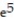
-
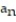 =
= 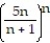
A) 0
B) 5
C) does not exist
D)

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
58
Find the limit of the sequence or determine that the limit does not exist.
-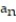 = ln
= ln 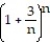
A) 0
B) 3
C) does not exist
D) ln 3
-
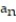 = ln
= ln 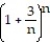
A) 0
B) 3
C) does not exist
D) ln 3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
59
Find the limit of the sequence or determine that the limit does not exist.
-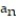 =
= 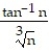
A) 0
B) 1
C)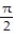
D) does not exist
-
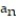 =
= 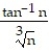
A) 0
B) 1
C)
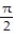
D) does not exist

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
60
Find the limit of the sequence or determine that the limit does not exist.
-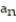 = n -
= n - 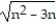
A)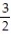
B)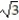
C) does not exist
D) 0
-
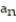 = n -
= n - 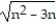
A)
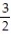
B)
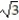
C) does not exist
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
61
Find the limit of the sequence or determine that the sequence diverges.
-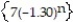
A) 7
B) The sequence diverges.
C) - 7
D) 0
-
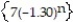
A) 7
B) The sequence diverges.
C) - 7
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
-A patient takes 100 mg of medication every 24 hours. 80% of the medication in the blood is eliminated every 24 hours.
a. Let dn equal the amount of medication (in mg) in the blood stream after n doses, where d1 = 100. Find a recurrence relation for dn .
b. Show that (dn) is monotonic and bounded, and therefore converges.
c. Find the limit of the sequence. What is the physical meaning of this limit?
A) a. dn + 1 = 0.2 dn + 100, d1 d1 = 100
b. dn satisfies 0 ≤ dn ≤ 125 for n ≥ 1 and its terms are increasing in size.
c. 125; in the long run there will be approximately 125 mg of medication in the blood.
B) a. dn + 1 = 0.8 dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 150 for n ≥ 1 and its terms are increasing in size.
c. 150; in the long run there will be approximately 150 mg of medication in the blood.
C) a. dn + 1 = 0.2 dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 150 for n ≥ 1 and its terms are increasing in size.
c. 150; in the long run there will be approximately 150 mg of medication in the blood.
D) a. dn + 1 = 0.8dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 125 for n ≥ 1 and its terms are increasing in size.
c. 125; in the long run there will be approximately 125 mg of medication in the blood.
-A patient takes 100 mg of medication every 24 hours. 80% of the medication in the blood is eliminated every 24 hours.
a. Let dn equal the amount of medication (in mg) in the blood stream after n doses, where d1 = 100. Find a recurrence relation for dn .
b. Show that (dn) is monotonic and bounded, and therefore converges.
c. Find the limit of the sequence. What is the physical meaning of this limit?
A) a. dn + 1 = 0.2 dn + 100, d1 d1 = 100
b. dn satisfies 0 ≤ dn ≤ 125 for n ≥ 1 and its terms are increasing in size.
c. 125; in the long run there will be approximately 125 mg of medication in the blood.
B) a. dn + 1 = 0.8 dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 150 for n ≥ 1 and its terms are increasing in size.
c. 150; in the long run there will be approximately 150 mg of medication in the blood.
C) a. dn + 1 = 0.2 dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 150 for n ≥ 1 and its terms are increasing in size.
c. 150; in the long run there will be approximately 150 mg of medication in the blood.
D) a. dn + 1 = 0.8dn + 100, d1 = 100
b. dn satisfies 0 ≤ dn ≤ 125 for n ≥ 1 and its terms are increasing in size.
c. 125; in the long run there will be approximately 125 mg of medication in the blood.

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
63
Find the limit of the sequence or state that it diverges.
-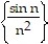
A) 0
B) -1
C) diverges
D) 1
-
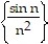
A) 0
B) -1
C) diverges
D) 1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
64
Find the limit of the sequence or state that it diverges.
-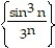
A) 0
B) diverges
C) 1
D) -1
-
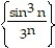
A) 0
B) diverges
C) 1
D) -1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
65
Determine if the geometric series converges or diverges. If it converges, find its sum.
-1 +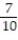 +
+ 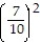 +
+ 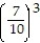 +
+ 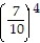 + . . .
+ . . .
A) converges, 3
B) diverges
C) converges,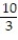
D) converges,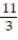
-1 +
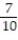 +
+ 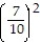 +
+ 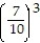 +
+ 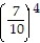 + . . .
+ . . .A) converges, 3
B) diverges
C) converges,
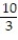
D) converges,
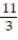

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
66
Determine if the geometric series converges or diverges. If it converges, find its sum.
-1 + ( -9) +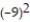 +
+ 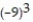 +
+ 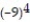 + . . .
+ . . .
A) converges, 9
B) converges, 81
C) diverges
D) converges, 90
-1 + ( -9) +
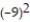 +
+ 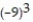 +
+ 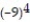 + . . .
+ . . .A) converges, 9
B) converges, 81
C) diverges
D) converges, 90

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
67
Determine if the geometric series converges or diverges. If it converges, find its sum.
-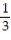 +
+ 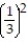 +
+ 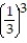 +
+ 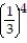 +
+ 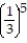 + . . .
+ . . .
A) converges,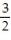
B) diverges
C) converges,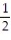
D) converges,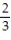
-
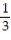 +
+ 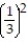 +
+ 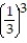 +
+ 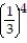 +
+ 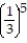 + . . .
+ . . .A) converges,
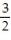
B) diverges
C) converges,
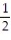
D) converges,
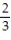

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
68
Find the sum of the series.
-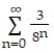
A) 24/7
B) 3/7
C) 8/3
D) 1/3
-
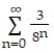
A) 24/7
B) 3/7
C) 8/3
D) 1/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
69
Find the sum of the series.
-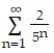
A) 1/2
B) 5/3
C) 1/3
D) 5/2
-
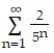
A) 1/2
B) 5/3
C) 1/3
D) 5/2

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
70
Find the sum of the series.
-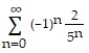
A) 5/2
B) 1/2
C) 1/3
D) 5/3
-
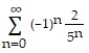
A) 5/2
B) 1/2
C) 1/3
D) 5/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
71
Find the sum of the series.
-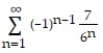
A) 42/5
B) 6
C) 1
D) 7/5
-
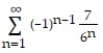
A) 42/5
B) 6
C) 1
D) 7/5

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
72
Find the sum of the series.
-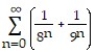
A) 23/8
B) 143/56
C) 145/56
D) 127/56
-
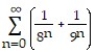
A) 23/8
B) 143/56
C) 145/56
D) 127/56

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
73
Find the sum of the series.
-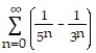
A) 1/4
B) 1
C) - 1/4
D) -1
-
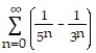
A) 1/4
B) 1
C) - 1/4
D) -1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
74
Find the sum of the series.
-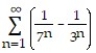
A) 5/6
B) - 5/6
C) - 1/3
D) 1/3
-
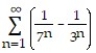
A) 5/6
B) - 5/6
C) - 1/3
D) 1/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
75
Find the sum of the series.
-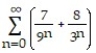
A) - 33/8
B) 3/10
C) 159/8
D) 123/10
-
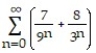
A) - 33/8
B) 3/10
C) 159/8
D) 123/10

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
76
Find the sum of the series.
-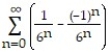
A) 12/37
B) 6/37
C) 6/35
D) 12/35
-
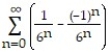
A) 12/37
B) 6/37
C) 6/35
D) 12/35

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
77
Find the sum of the series.
-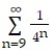
A) 65536/3
B) 1/ 786432
C) 262144/3
D) 1/196608
-
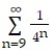
A) 65536/3
B) 1/ 786432
C) 262144/3
D) 1/196608

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
78
Express the number as the ratio of two integers.
-0.77777 . . .
A) 7/99
B) 70/99
C) 7/9
D) 70/999
-0.77777 . . .
A) 7/99
B) 70/99
C) 7/9
D) 70/999

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
79
Express the number as the ratio of two integers.
-0.747474 . . .
A) 74/99
B) 20/27
C) 740/99
D) 2/27
-0.747474 . . .
A) 74/99
B) 20/27
C) 740/99
D) 2/27

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
80
Express the number as the ratio of two integers.
-0.5303030 . . .
A) 175/33
B) 35/22
C) 35/66
D) 35/33
-0.5303030 . . .
A) 175/33
B) 35/22
C) 35/66
D) 35/33

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck


