Deck 11: Boundary Value Problems and Sturm-Liouville Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 11: Boundary Value Problems and Sturm-Liouville Theory
1
Consider the boundary value problem 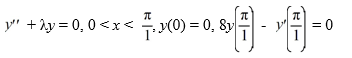
Which of the following statements are true? Select all that apply.
A) = 0 is an eigenvalue.
B) There is one negative eigenvalue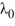 = -
= - 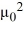 such that tanh
such that tanh 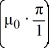 =
= 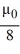 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 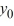 (x) = C sinh(
(x) = C sinh( 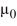 x), where C is an arbitrary nonzero real constant.
x), where C is an arbitrary nonzero real constant.
C) There are infinitely many positive eigenvalues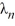 = -
= - 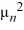 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 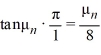 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 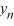 (x) =
(x) = 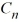 sin(
sin( 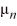 x), where
x), where 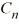 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.
D) There are infinitely many negative eigenvalues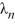 = -
= - 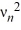 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 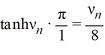 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 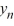 (x) =
(x) = 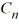 sin(
sin( 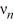 x), where
x), where 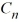 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.
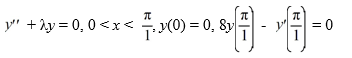
Which of the following statements are true? Select all that apply.
A) = 0 is an eigenvalue.
B) There is one negative eigenvalue
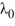 = -
= - 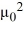 such that tanh
such that tanh 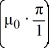 =
= 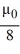 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 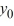 (x) = C sinh(
(x) = C sinh( 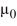 x), where C is an arbitrary nonzero real constant.
x), where C is an arbitrary nonzero real constant.C) There are infinitely many positive eigenvalues
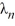 = -
= - 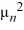 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 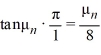 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 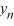 (x) =
(x) = 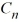 sin(
sin( 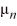 x), where
x), where 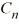 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.D) There are infinitely many negative eigenvalues
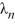 = -
= - 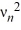 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 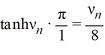 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 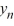 (x) =
(x) = 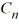 sin(
sin( 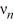 x), where
x), where 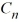 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.There is one negative eigenvalue 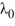 = -
= - 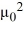 such that tanh
such that tanh 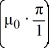 =
= 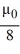 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 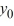 (x) = C sinh(
(x) = C sinh( 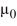 x), where C is an arbitrary nonzero real constant.
x), where C is an arbitrary nonzero real constant.
There are infinitely many positive eigenvalues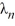 = -
= - 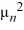 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 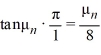 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 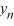 (x) =
(x) = 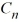 sin(
sin( 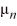 x), where
x), where 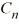 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant.
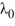 = -
= - 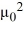 such that tanh
such that tanh 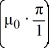 =
= 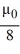 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 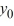 (x) = C sinh(
(x) = C sinh( 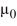 x), where C is an arbitrary nonzero real constant.
x), where C is an arbitrary nonzero real constant.There are infinitely many positive eigenvalues
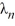 = -
= - 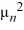 , n = 1, 2, 3, ... such that
, n = 1, 2, 3, ... such that 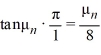 ; the corresponding eigenvectors are
; the corresponding eigenvectors are 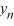 (x) =
(x) = 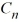 sin(
sin( 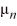 x), where
x), where 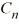 is an arbitrary nonzero real constant.
is an arbitrary nonzero real constant. 2
Consider the boundary value problem
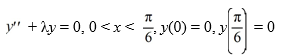
Which of the following is a complete list of the eigenvalue-eigenvector pairs for this boundary value problem?
A)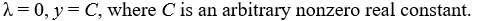
B)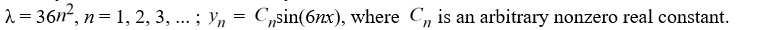
C)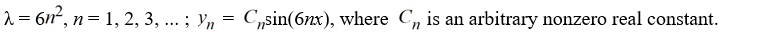
D)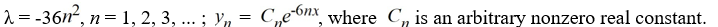
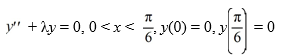
Which of the following is a complete list of the eigenvalue-eigenvector pairs for this boundary value problem?
A)
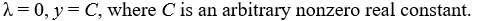
B)
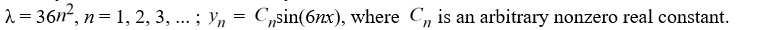
C)
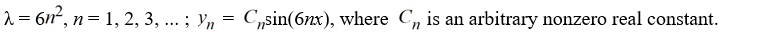
D)
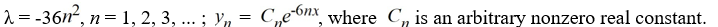
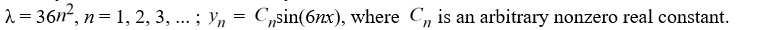
3
Consider the boundary value problem
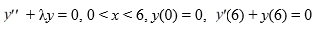
Which of the following statements are true? Select all that apply.
A) There are infinitely many negative eigenvalues = -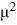 satisfying the equation
satisfying the equation 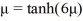 .
.
B) The positive eigenvalue satisfies the equation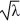 = -tan(6
= -tan(6 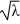 ).
).
C) = 0 is an eigenvalue.
D) There are no negative eigenvalues.
E) = 0 is not an eigenvalue.
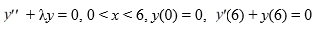
Which of the following statements are true? Select all that apply.
A) There are infinitely many negative eigenvalues = -
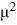 satisfying the equation
satisfying the equation 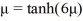 .
.B) The positive eigenvalue satisfies the equation
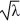 = -tan(6
= -tan(6 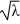 ).
).C) = 0 is an eigenvalue.
D) There are no negative eigenvalues.
E) = 0 is not an eigenvalue.
The positive eigenvalue satisfies the equation 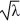 = -tan(6
= -tan(6 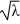 ).
).
There are no negative eigenvalues.
= 0 is not an eigenvalue.
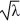 = -tan(6
= -tan(6 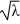 ).
).There are no negative eigenvalues.
= 0 is not an eigenvalue.
4
Consider the Sturm-Liouville problem
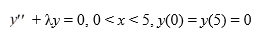
Given the eigenfunctions of this boundary value problem are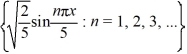 .
.
Using this as an orthonormal basis, which of the following is the eigenfunction expansion of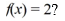
A)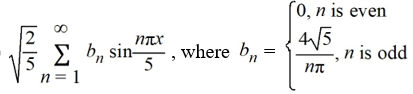
B)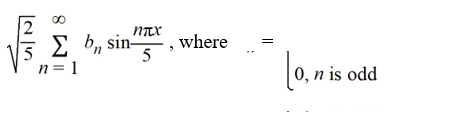
C)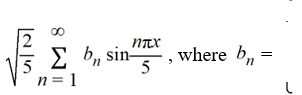
D)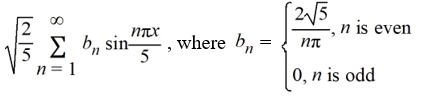
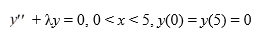
Given the eigenfunctions of this boundary value problem are
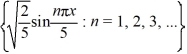 .
.Using this as an orthonormal basis, which of the following is the eigenfunction expansion of
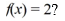
A)
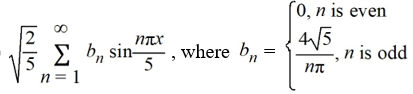
B)
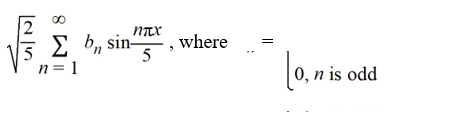
C)
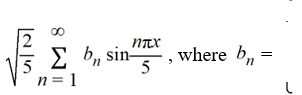
D)
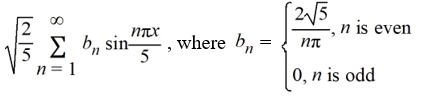

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the Sturm-Liouville problem

eigenfunction expansion of f(x) = 7x?

eigenfunction expansion of f(x) = 7x?

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the boundary value problem
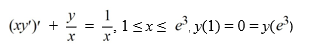
This equation is in self-adjoint form.
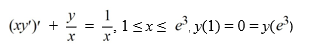
This equation is in self-adjoint form.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the boundary value problem

A)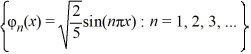
B)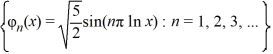
C)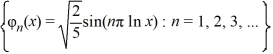
D)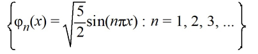

A)
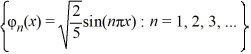
B)
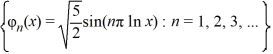
C)
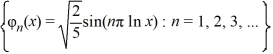
D)
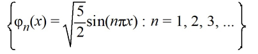

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the boundary value problem
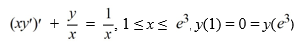
What is the eigenfunction expansion of the solution y(x) of this boundary value problem?
A)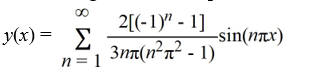
B)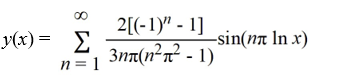
C)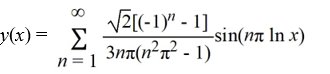
D)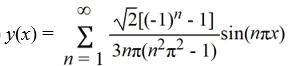
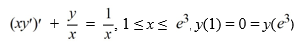
What is the eigenfunction expansion of the solution y(x) of this boundary value problem?
A)
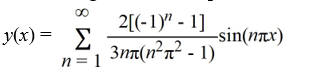
B)
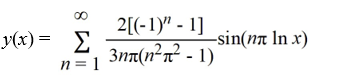
C)
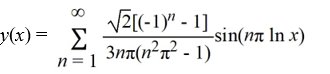
D)
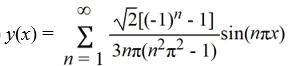

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
Determine the eigenfunctions for the eigenvalue problem
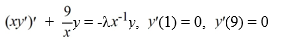
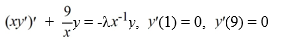

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the eigenfunction problem
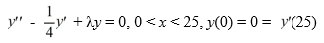
What are the eigenvalues?
A)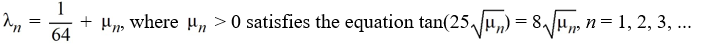
B)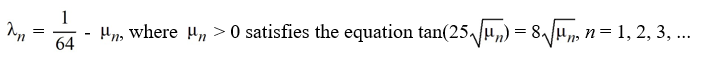
C)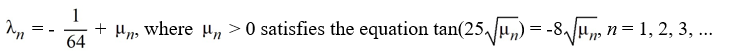
D)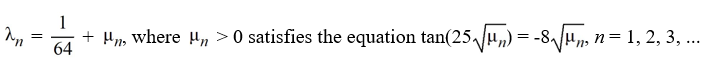
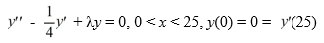
What are the eigenvalues?
A)
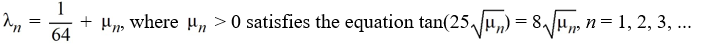
B)
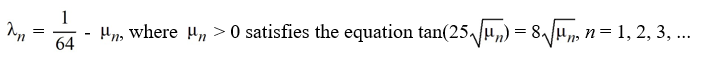
C)
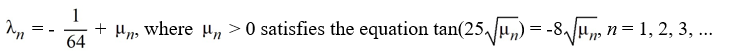
D)
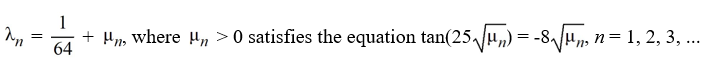

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the eigenfunction problem
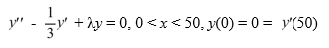
What are the corresponding eigenfunctions?
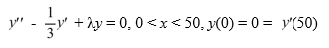
What are the corresponding eigenfunctions?

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the eigenfunction problem



Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the boundary value problem
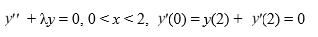
Which of these equations do the eigenvalues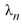 satisfy?
satisfy?
A) sin(2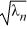 ) +
) + 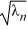 cos(2
cos(2 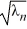 ) = 0, n = 1, 2, 3, ...
) = 0, n = 1, 2, 3, ...
B) sin(2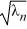 ) -
) - 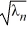 cos(2
cos(2 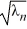 ) = 0, n = 1, 2, 3, ...
) = 0, n = 1, 2, 3, ...
C)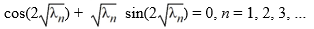
D)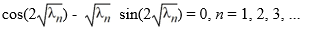
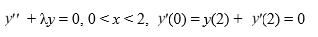
Which of these equations do the eigenvalues
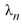 satisfy?
satisfy?A) sin(2
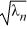 ) +
) + 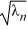 cos(2
cos(2 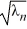 ) = 0, n = 1, 2, 3, ...
) = 0, n = 1, 2, 3, ...B) sin(2
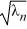 ) -
) - 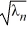 cos(2
cos(2 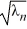 ) = 0, n = 1, 2, 3, ...
) = 0, n = 1, 2, 3, ...C)
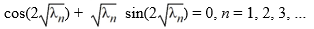
D)
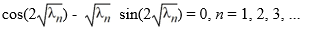

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the boundary value problem 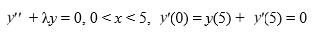
Determine the normalized eigenfunctions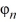 (x).
(x).
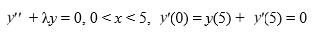
Determine the normalized eigenfunctions
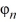 (x).
(x).
Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the boundary value problem
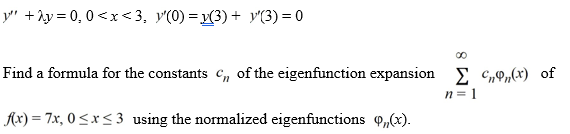
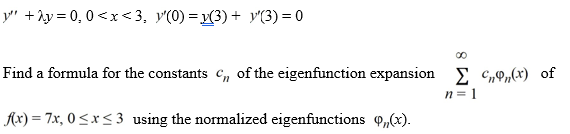

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the boundary value problem
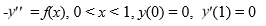
Which of these is the Green's function for this boundary value problem?
A)
B)
C)
D)
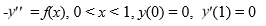
Which of these is the Green's function for this boundary value problem?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the boundary value problem
-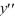 = f(x), 0 < x < 1, y(0) = 0,
= f(x), 0 < x < 1, y(0) = 0, 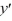 (1) = 0
(1) = 0
Which of these is the Green's function representation of the solution of the given boundary value problem?
A)
B)
C)
D)
-
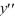 = f(x), 0 < x < 1, y(0) = 0,
= f(x), 0 < x < 1, y(0) = 0, 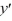 (1) = 0
(1) = 0Which of these is the Green's function representation of the solution of the given boundary value problem?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the boundary value problem
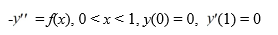
Evaluate the Green's function representation of the solution when f(x) = 17x + 9, 0 ≤ x ≤ 1.
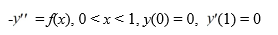
Evaluate the Green's function representation of the solution when f(x) = 17x + 9, 0 ≤ x ≤ 1.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
The singular Sturm-Liouville boundary value problem consisting of the differential equation 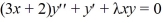 with boundary conditions that both y and
with boundary conditions that both y and 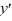 remain bounded as x approaches 0 from the right and that y(1) +
remain bounded as x approaches 0 from the right and that y(1) + 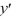 (1) = 0 is self-adjoint.
(1) = 0 is self-adjoint.
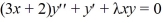 with boundary conditions that both y and
with boundary conditions that both y and 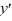 remain bounded as x approaches 0 from the right and that y(1) +
remain bounded as x approaches 0 from the right and that y(1) + 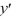 (1) = 0 is self-adjoint.
(1) = 0 is self-adjoint. 
Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


