Deck 10: Partial Differential Equations and Fourier Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/44
Play
Full screen (f)
Deck 10: Partial Differential Equations and Fourier Series
1
Which of the following represents all solutions of the boundary value problem 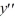 + 36y = 0, y (0) = 1, y ( ) = 1?
+ 36y = 0, y (0) = 1, y ( ) = 1?
A) y = 0
B) y = 1
C) y =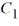 cos(6x) +
cos(6x) + 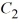 sin(6x), where
sin(6x), where 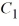 and
and 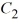 are arbitrary real constants
are arbitrary real constants
D) y = cos(6x) +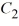 sin(6x), where
sin(6x), where 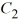 is an arbitrary real constant
is an arbitrary real constant
E) y =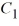 cos(6x) + sin(6x), where
cos(6x) + sin(6x), where 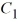 is an arbitrary real constant
is an arbitrary real constant
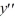 + 36y = 0, y (0) = 1, y ( ) = 1?
+ 36y = 0, y (0) = 1, y ( ) = 1?A) y = 0
B) y = 1
C) y =
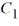 cos(6x) +
cos(6x) + 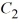 sin(6x), where
sin(6x), where 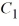 and
and 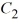 are arbitrary real constants
are arbitrary real constantsD) y = cos(6x) +
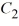 sin(6x), where
sin(6x), where 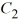 is an arbitrary real constant
is an arbitrary real constantE) y =
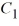 cos(6x) + sin(6x), where
cos(6x) + sin(6x), where 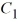 is an arbitrary real constant
is an arbitrary real constanty = cos(6x) + 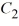 sin(6x), where
sin(6x), where 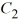 is an arbitrary real constant
is an arbitrary real constant
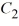 sin(6x), where
sin(6x), where 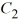 is an arbitrary real constant
is an arbitrary real constant 2
Consider the boundary value problem 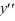 + 9y = 0, y (0) = 3, y ( ) = 0
+ 9y = 0, y (0) = 3, y ( ) = 0
Which of these statements is true?
A) This boundary value problem has no solution.
B) y = 3 cos(3x) - 3 sin(3x) is the unique solution of this boundary value problem.
C) There are infinitely many solutions of this boundary value problem of the form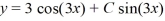 , where C is an arbitrary real constant.
, where C is an arbitrary real constant.
D) y = 0 is a solution of this boundary value problem.
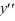 + 9y = 0, y (0) = 3, y ( ) = 0
+ 9y = 0, y (0) = 3, y ( ) = 0Which of these statements is true?
A) This boundary value problem has no solution.
B) y = 3 cos(3x) - 3 sin(3x) is the unique solution of this boundary value problem.
C) There are infinitely many solutions of this boundary value problem of the form
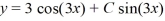 , where C is an arbitrary real constant.
, where C is an arbitrary real constant.D) y = 0 is a solution of this boundary value problem.
This boundary value problem has no solution.
3
Consider the boundary value problem 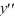 + 25y = 0, y (0) = -2, y
+ 25y = 0, y (0) = -2, y  = 0Which of these statements is true?
= 0Which of these statements is true?
A) This boundary value problem has no solution.
B) y = -2 cos(5x) + C sin(5x) is a solution of this boundary value problem, for any real constant C.
C) y = -2 cos(5x) is the unique solution of this boundary value problem.
D) y = 0 is the unique solution of this boundary value problem.
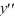 + 25y = 0, y (0) = -2, y
+ 25y = 0, y (0) = -2, y  = 0Which of these statements is true?
= 0Which of these statements is true?A) This boundary value problem has no solution.
B) y = -2 cos(5x) + C sin(5x) is a solution of this boundary value problem, for any real constant C.
C) y = -2 cos(5x) is the unique solution of this boundary value problem.
D) y = 0 is the unique solution of this boundary value problem.
y = -2 cos(5x) is the unique solution of this boundary value problem.
4
Consider the boundary value problem 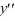 + 49y = 0, y (0) = -5, y
+ 49y = 0, y (0) = -5, y  = 0Which of these statements is true?
= 0Which of these statements is true?
A) This boundary value problem has no solution.
B) y = -5 cos(7x) + C sin(7x) is a solution of this boundary value problem, for any real constant C.
C) y = -5 cos(7x) - 5 sin(7x) is the unique solution of this boundary value problem.
D) y = -5 cos(7x) + 5 sin(7x) is the unique solution of this boundary value problem.
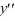 + 49y = 0, y (0) = -5, y
+ 49y = 0, y (0) = -5, y  = 0Which of these statements is true?
= 0Which of these statements is true?A) This boundary value problem has no solution.
B) y = -5 cos(7x) + C sin(7x) is a solution of this boundary value problem, for any real constant C.
C) y = -5 cos(7x) - 5 sin(7x) is the unique solution of this boundary value problem.
D) y = -5 cos(7x) + 5 sin(7x) is the unique solution of this boundary value problem.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the boundary value problem 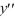 + 25y = 0, y (0) = 0, y
+ 25y = 0, y (0) = 0, y  = 0Which of the following are eigenvalues for this boundary value problem? Select all that apply.
= 0Which of the following are eigenvalues for this boundary value problem? Select all that apply.
A)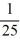
B) 25
C)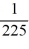
D)
E) 225
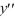 + 25y = 0, y (0) = 0, y
+ 25y = 0, y (0) = 0, y  = 0Which of the following are eigenvalues for this boundary value problem? Select all that apply.
= 0Which of the following are eigenvalues for this boundary value problem? Select all that apply.A)
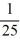
B) 25
C)
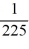
D)

E) 225

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
6
Assume that > 0. Consider the boundary value problem 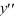 + ?y = 0, y (0) = 0,
+ ?y = 0, y (0) = 0, 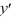 (6) = 0
(6) = 0
Which of the following are eigenvectors for this boundary value problem? Select all that apply.
A) y = 3 sin(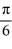 x)
x)
B) y = -0.2 cos(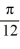 x)
x)
C) y = 0.2 sin(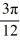 x)
x)
D) y = 3 sin(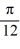 x)
x)
E) y = -3 cos(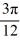 x)
x)
F) y = sin(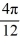 x)
x)
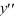 + ?y = 0, y (0) = 0,
+ ?y = 0, y (0) = 0, 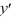 (6) = 0
(6) = 0Which of the following are eigenvectors for this boundary value problem? Select all that apply.
A) y = 3 sin(
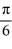 x)
x)B) y = -0.2 cos(
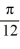 x)
x)C) y = 0.2 sin(
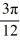 x)
x)D) y = 3 sin(
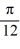 x)
x)E) y = -3 cos(
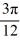 x)
x)F) y = sin(
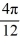 x)
x)
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
7
What is the fundamental period of the periodic function f (x) = cos 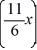 ?
?
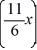 ?
?
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the following periodic function with period 6:
H(t) =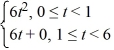
H(t + 12) = H(t)
The Fourier series representation for H(t) has the form
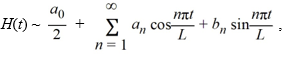
where 12 is the period of H(t). What is the coefficient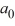 ? Express your answer as a simplified fraction.
? Express your answer as a simplified fraction.
H(t) =
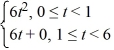
H(t + 12) = H(t)
The Fourier series representation for H(t) has the form
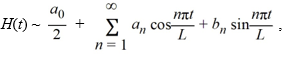
where 12 is the period of H(t). What is the coefficient
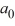 ? Express your answer as a simplified fraction.
? Express your answer as a simplified fraction.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the following periodic function with period 9:
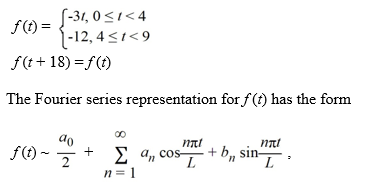
where 18 is the period of f (t). What is the coefficient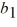 ? Express your answer in exact form involving π. Do not approximate.
? Express your answer in exact form involving π. Do not approximate.
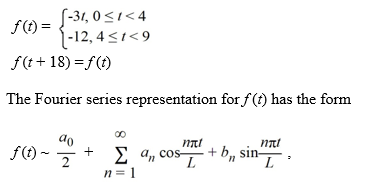
where 18 is the period of f (t). What is the coefficient
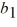 ? Express your answer in exact form involving π. Do not approximate.
? Express your answer in exact form involving π. Do not approximate.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following periodic function with period 4:
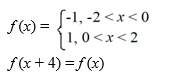
Which of these is the Fourier representation for f (t)?
A)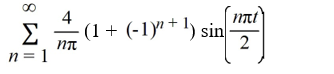
B)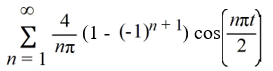
C)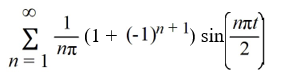
D)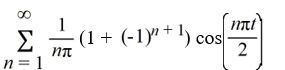
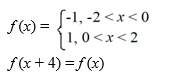
Which of these is the Fourier representation for f (t)?
A)
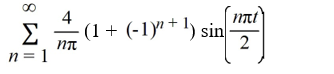
B)
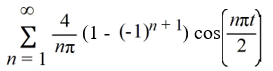
C)
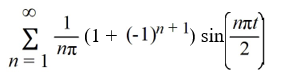
D)
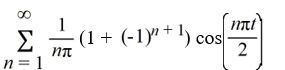

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the following periodic function with period 8:
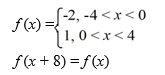
Which of these is the Fourier representation for f (x)?
A)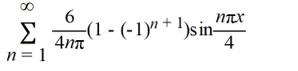
B)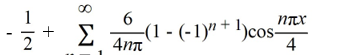
C)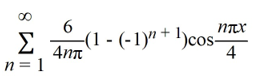
D)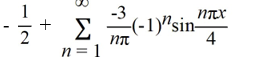
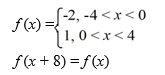
Which of these is the Fourier representation for f (x)?
A)
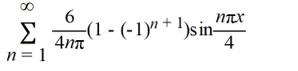
B)
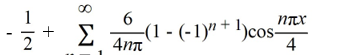
C)
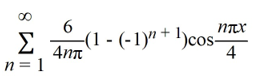
D)
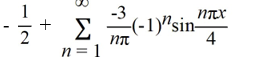

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose f (x) is defined by f (x) = 4 ![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a4_9020_139e2ca21f0e_TBW1042_11.jpg) on the interval [0, 9]. Consider the function
on the interval [0, 9]. Consider the function
![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a5_9020_fbc504f18c0e_TBW1042_00.jpg)
Compute F![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a6_9020_eb1c6c3e4095_TBW1042_11.jpg) .
.
![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a4_9020_139e2ca21f0e_TBW1042_11.jpg) on the interval [0, 9]. Consider the function
on the interval [0, 9]. Consider the function ![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a5_9020_fbc504f18c0e_TBW1042_00.jpg)
Compute F
![Suppose f (x) is defined by f (x) = 4 on the interval [0, 9]. Consider the function Compute F .](https://storage.examlex.com/TBW1042/11eeb833_7036_b3a6_9020_eb1c6c3e4095_TBW1042_11.jpg) .
.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose f (x) is defined by f (x) = 8 ![Suppose f (x) is defined by f (x) = 8 on the interval [0, 9]. Consider the function Compute F(-8).](https://storage.examlex.com/TBW1042/11eeb833_7036_dab8_9020_5b99ebd9a963_TBW1042_11.jpg) on the interval [0, 9]. Consider the function
on the interval [0, 9]. Consider the function
![Suppose f (x) is defined by f (x) = 8 on the interval [0, 9]. Consider the function Compute F(-8).](https://storage.examlex.com/TBW1042/11eeb833_7036_dab9_9020_5d4a10ac9331_TBW1042_00.jpg)
Compute F(-8).
![Suppose f (x) is defined by f (x) = 8 on the interval [0, 9]. Consider the function Compute F(-8).](https://storage.examlex.com/TBW1042/11eeb833_7036_dab8_9020_5b99ebd9a963_TBW1042_11.jpg) on the interval [0, 9]. Consider the function
on the interval [0, 9]. Consider the function ![Suppose f (x) is defined by f (x) = 8 on the interval [0, 9]. Consider the function Compute F(-8).](https://storage.examlex.com/TBW1042/11eeb833_7036_dab9_9020_5d4a10ac9331_TBW1042_00.jpg)
Compute F(-8).

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the following periodic function with period 5:
f (t) =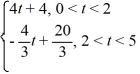
f (t + 5) = f (t)
To what value does the Fourier series for f (t) converge for t = 4?
f (t) =
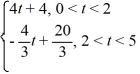
f (t + 5) = f (t)
To what value does the Fourier series for f (t) converge for t = 4?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the following periodic function with period 4:
f (t) =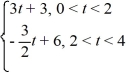
f (t + 4) = f (t)
To what value does the Fourier series for f (t) converge for t = 2?
f (t) =
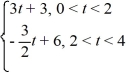
f (t + 4) = f (t)
To what value does the Fourier series for f (t) converge for t = 2?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the following periodic function with period 6:
f (t) =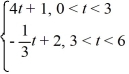
f (t + 6) = f (t)
To what value does the Fourier series for f (t) converge for t = 2?
f (t) =
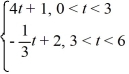
f (t + 6) = f (t)
To what value does the Fourier series for f (t) converge for t = 2?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the following periodic function with period 7:
f (t) =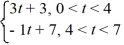
f (t + 7) = f (t)
To what value does the Fourier series for f (t) converge for t = 0?
f (t) =
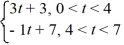
f (t + 7) = f (t)
To what value does the Fourier series for f (t) converge for t = 0?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the following periodic function with period 5:
f (t) =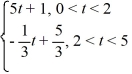
f (t + 5) = f (t)
To what value does the Fourier series for f (t) converge for t = 5?
f (t) =
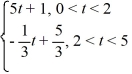
f (t + 5) = f (t)
To what value does the Fourier series for f (t) converge for t = 5?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the following periodic function with period 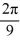 :
:
f (t) =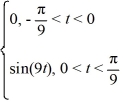
f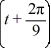 = f (t)
= f (t)
The Fourier representation has the form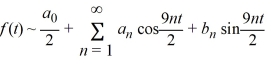
Compute f , where m is an odd integer.
, where m is an odd integer.
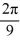 :
:f (t) =
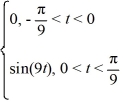
f
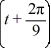 = f (t)
= f (t)The Fourier representation has the form
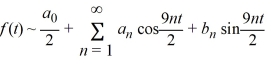
Compute f
 , where m is an odd integer.
, where m is an odd integer.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the following periodic function with period 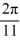 :
:
f (t) =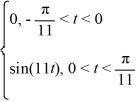 f
f 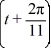 = f (t)
= f (t)
The Fourier representation has the form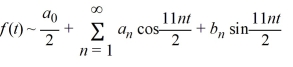
What is the value of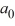 ?
?
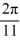 :
:f (t) =
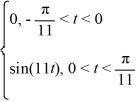 f
f 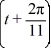 = f (t)
= f (t)The Fourier representation has the form
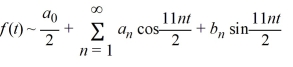
What is the value of
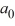 ?
?
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the following periodic function with period 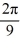 :
:
F (t) =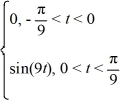
F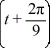 = f (t)
= f (t)
The Fourier representation has the form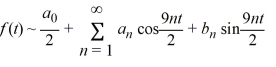
Which of these are the coefficients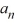 ?
?
A)
B)
C)
D)
E)
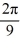 :
:F (t) =
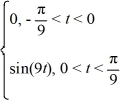
F
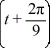 = f (t)
= f (t)The Fourier representation has the form
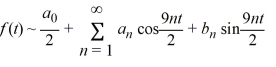
Which of these are the coefficients
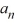 ?
?A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the following periodic function with period 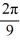 :
:
F (t) =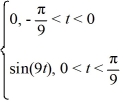
F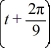 = f (t)
= f (t)
The Fourier representation has the form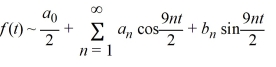
Which of these are the coefficients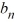 ?
?
A)
B)
C)
D)
E)
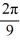 :
:F (t) =
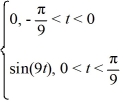
F
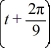 = f (t)
= f (t)The Fourier representation has the form
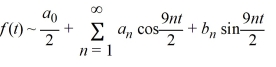
Which of these are the coefficients
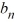 ?
?A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following periodic function with period 2?:
F (t) =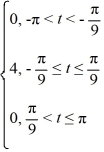
F (t + 2 ) = f (t)
Which of these is the Fourier representation for f (t)?
A)
B)
C)
D)
F (t) =
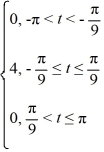
F (t + 2 ) = f (t)
Which of these is the Fourier representation for f (t)?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the following periodic function with period 4π:
f (t) = 5t, -2π < t ≤ 2π
f (t + 4π) = f (t)
What is the Fourier series representation for f (t)?
f (t) = 5t, -2π < t ≤ 2π
f (t + 4π) = f (t)
What is the Fourier series representation for f (t)?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the following periodic function with period 4π:
f (t) = 4t, -2π < t ≤ 2π
f (t + 4π) = f (t)
To what value does the Fourier series converge when t = -8π?
f (t) = 4t, -2π < t ≤ 2π
f (t + 4π) = f (t)
To what value does the Fourier series converge when t = -8π?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following functions is even? Select all that apply.
A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following statements are true? Select all that apply.
A) If is an even function, then its graph is symmetric about the -axis.
B) is an odd function.
C) is an odd function.
D) If is an even function, then .
E) If is an odd function with the Fourier series representation
, then , for all .
A) If is an even function, then its graph is symmetric about the -axis.
B) is an odd function.
C) is an odd function.
D) If is an even function, then .
E) If is an odd function with the Fourier series representation
, then , for all .

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the function f (x) = 7 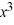 + 3
+ 3 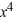 . Which of the following is the even periodic extension of f (x)?
. Which of the following is the even periodic extension of f (x)?
A)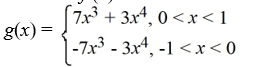
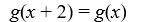
B)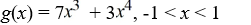
C)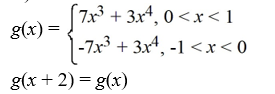
D)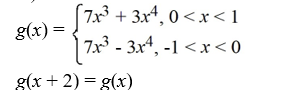
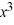 + 3
+ 3 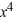 . Which of the following is the even periodic extension of f (x)?
. Which of the following is the even periodic extension of f (x)?A)
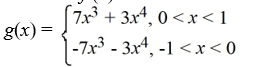
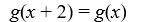
B)
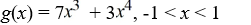
C)
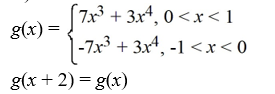
D)
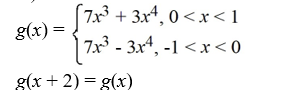

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the function f (x) = 5 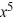 + 3
+ 3 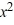 . Which of the following is the odd periodic extension of f (x)?
. Which of the following is the odd periodic extension of f (x)?
A)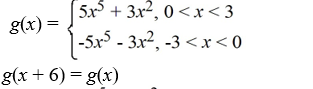
B)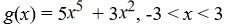
C)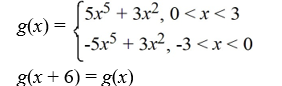
D)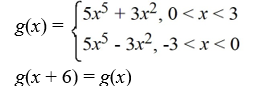
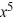 + 3
+ 3 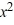 . Which of the following is the odd periodic extension of f (x)?
. Which of the following is the odd periodic extension of f (x)?A)
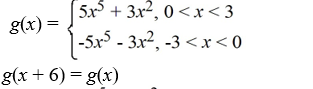
B)
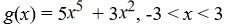
C)
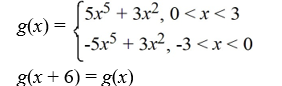
D)
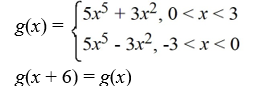

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the following function:
F (x) =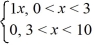
What is the Fourier cosine series for f (x)?
A)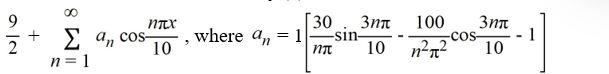
B)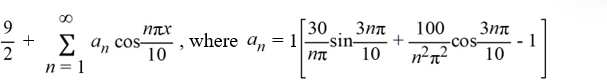
C)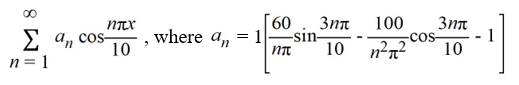
D)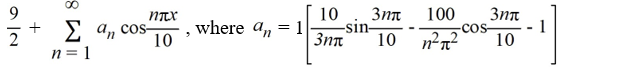
F (x) =
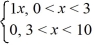
What is the Fourier cosine series for f (x)?
A)
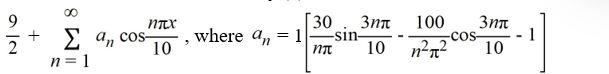
B)
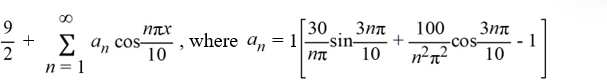
C)
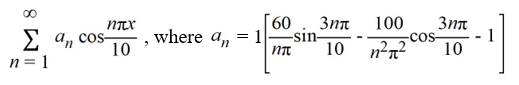
D)
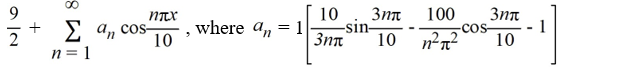

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following statements are true? Select all that apply.
A) The function f (x) defined by
F (x) = 2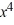 , 0 < x 4
, 0 < x 4
F (x + 4) = f (x)
Is even.
B) The odd periodic extension of f (x) = 5x, 0 < x < 1, is given by
G(x) =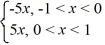
C) The function f (x) defined by
F (x) =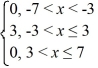
F (x + 14) = f (x)
Is even.
D) The even periodic extension of f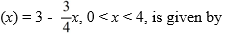
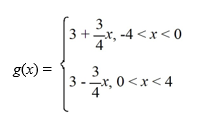
E) The Fourier series of the function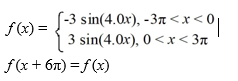
A) The function f (x) defined by
F (x) = 2
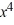 , 0 < x 4
, 0 < x 4F (x + 4) = f (x)
Is even.
B) The odd periodic extension of f (x) = 5x, 0 < x < 1, is given by
G(x) =
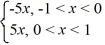
C) The function f (x) defined by
F (x) =
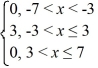
F (x + 14) = f (x)
Is even.
D) The even periodic extension of f
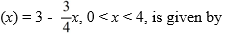
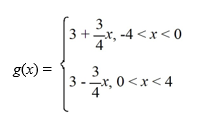
E) The Fourier series of the function
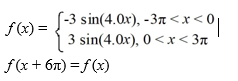

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
32
Find the Fourier series for f (x) = 4, 0 < x < 
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
33
For which of these partial differential equations can the method of separation of variables be used to reduce it to a pair of ordinary differential equations? Select all that apply.
A)
B)
C)
D) , where and are continuous functions
E)
F)
A)
B)
C)
D) , where and are continuous functions
E)
F)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
34
What is the solution of the following initial boundary value problem?
4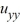 =
= 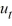 , u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)
, u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)
A)
B)
C)
D)
4
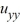 =
= 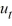 , u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)
, u(0, t) = 0, u(2, t) = 0, u(x, 0) = sin(4?x)A)
B)
C)
D)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the conduction of heat in a rod 30 cm in length whose ends are maintained at 0°C for all time t > 0. Find the expression for the temperature u(x, t) of position x in the rod at time t if the initial temperature distribution is given by
u(x, 0) =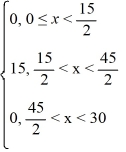
Assume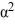 = 1 in the heat conduction partial differential equation.
= 1 in the heat conduction partial differential equation.
u(x, 0) =
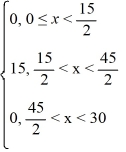
Assume
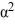 = 1 in the heat conduction partial differential equation.
= 1 in the heat conduction partial differential equation.
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
36
The ends of a rod 75 cm in length are connected to reservoirs that maintain the temperature at 11°C at x = 0 and 20°C at x = 75. The initial boundary value problem governing how heat conducts through the rod is as follows:
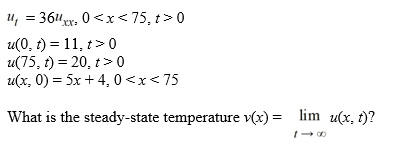
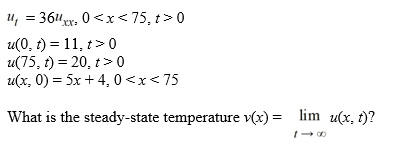

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
37
The ends of a rod 45 cm in length are connected to reservoirs that maintain the temperature at 13°C at x = 0 and 18°C at x = 45. The initial boundary value problem governing how heat conducts through the rod is as follows:
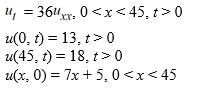
What is the transient temperature w(x, t) portion of the solution of the initial value boundary value problem?
A)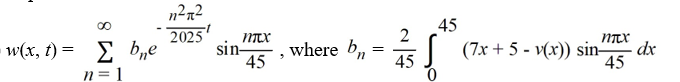
B)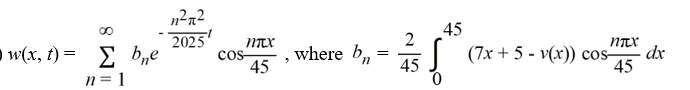
C)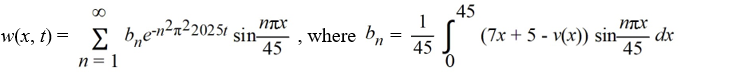
D)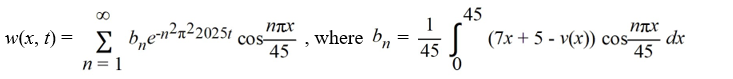
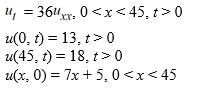
What is the transient temperature w(x, t) portion of the solution of the initial value boundary value problem?
A)
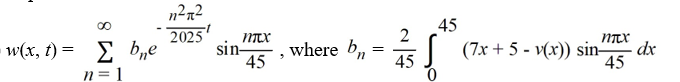
B)
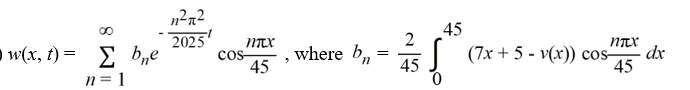
C)
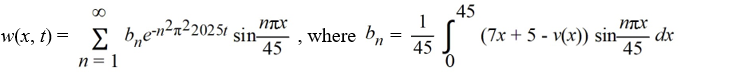
D)
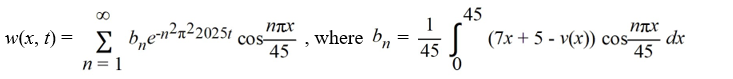

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
38
The ends of a rod 40 cm in length are connected to reservoirs that maintain the temperature at 12°C at x = 0 and 14°C at x = 40. The initial boundary value problem governing how heat conducts through the rod is as follows:
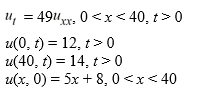
What is the solution u(x, t) of the initial boundary value problem?
A) u(x, t) = v(x) * w(x, t)
B) u(x, t) = v(x) + w(x, t) + C, where C is an arbitrary real constant.
C) u(x, t) = v(x) + w(x, t)
D) u(x, t) = w(x, t) - v(x)
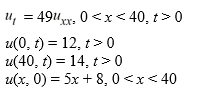
What is the solution u(x, t) of the initial boundary value problem?
A) u(x, t) = v(x) * w(x, t)
B) u(x, t) = v(x) + w(x, t) + C, where C is an arbitrary real constant.
C) u(x, t) = v(x) + w(x, t)
D) u(x, t) = w(x, t) - v(x)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
39
What is the steady state solution for the heat conduction equation
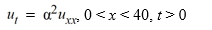
Equipped with the following boundary conditions:
U(0, t) - (0, t) = 5
U(40, t) + (40, t) = 4
A)
B)
C)
D)
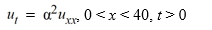
Equipped with the following boundary conditions:
U(0, t) - (0, t) = 5
U(40, t) + (40, t) = 4
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that both ends of a string of length 25 cm are attached to fixed points at height 0. Initially, the string is at rest and has shape 8 sin  , where x is the horizontal coordinate along
, where x is the horizontal coordinate along
the string with zero at the left end. The speed of wave propagation along the string is 2 cm per sec. Formulate an initial boundary value problem that describes the shape of the string, u(x, t), over time.
 , where x is the horizontal coordinate along
, where x is the horizontal coordinate along the string with zero at the left end. The speed of wave propagation along the string is 2 cm per sec. Formulate an initial boundary value problem that describes the shape of the string, u(x, t), over time.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose the following initial boundary value problem governs the shape of a string 60 cm long, where t is measured in minutes:
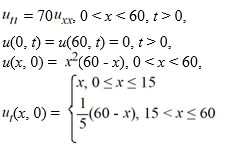
What is the speed of wave propagation along the string?
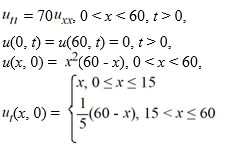
What is the speed of wave propagation along the string?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose the following initial boundary value problem governs the shape of a string 140 cm long, where t is measured in minutes:
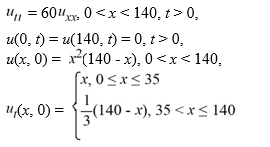
What is the initial displacement of the string at x = 110?
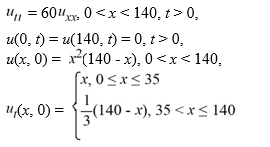
What is the initial displacement of the string at x = 110?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose the following initial boundary value problem governs the shape of a string 120 cm long, where t is measured in minutes:
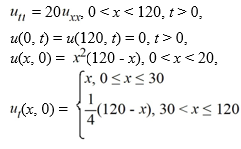
What is the initial velocity of the string at the point x = 90?
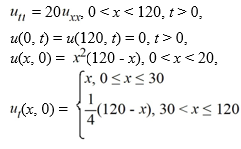
What is the initial velocity of the string at the point x = 90?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
44
Determine the function u(x, y) satisfying Laplace's equation 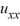 +
+ 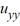 = 0 in the rectangle
= 0 in the rectangle 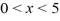 ,
, 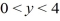 and satisfying the boundary conditionsu
and satisfying the boundary conditionsu
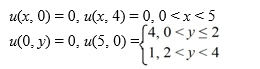
A)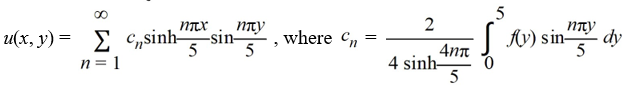
B)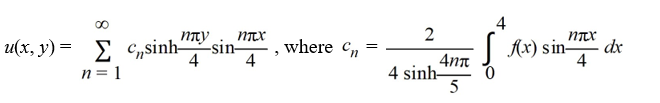
C)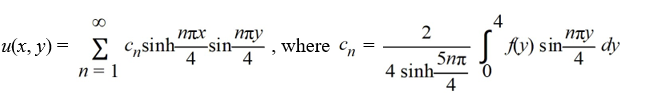
D)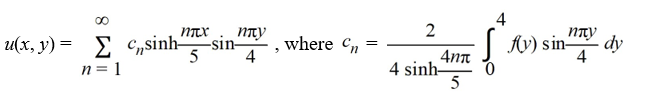
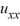 +
+ 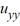 = 0 in the rectangle
= 0 in the rectangle 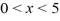 ,
, 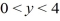 and satisfying the boundary conditionsu
and satisfying the boundary conditionsu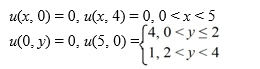
A)
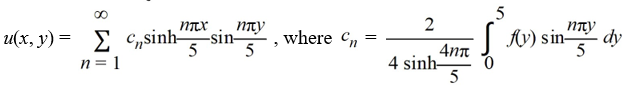
B)
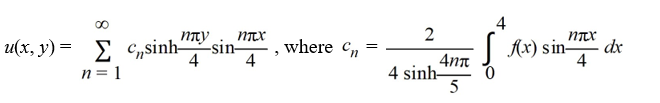
C)
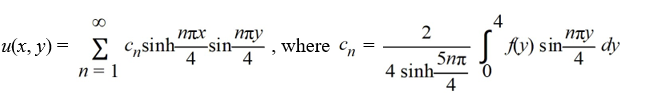
D)
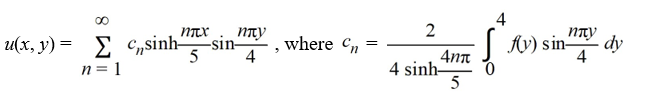

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck


